Digital Design Combinational Logic Design Chapter 2 Combinational

Digital Design - Combinational Logic Design Chapter 2 Combinational Logic Design

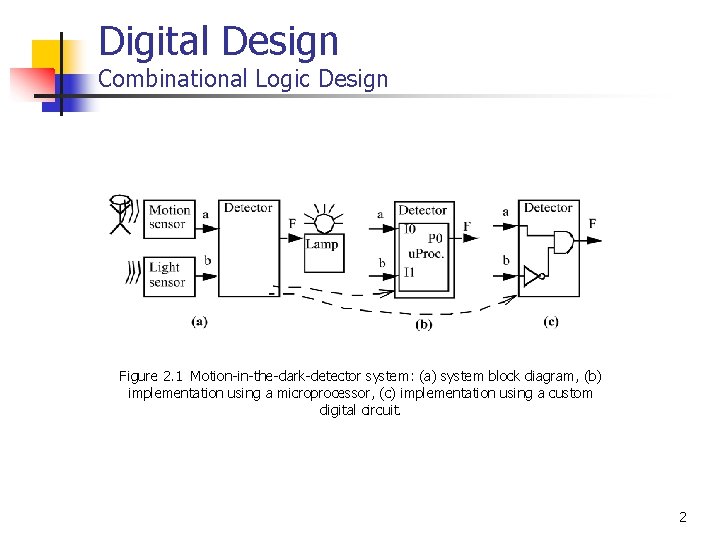
Digital Design Combinational Logic Design Figure 2. 1 Motion-in-the-dark-detector system: (a) system block diagram, (b) implementation using a microprocessor, (c) implementation using a custom digital circuit. 2

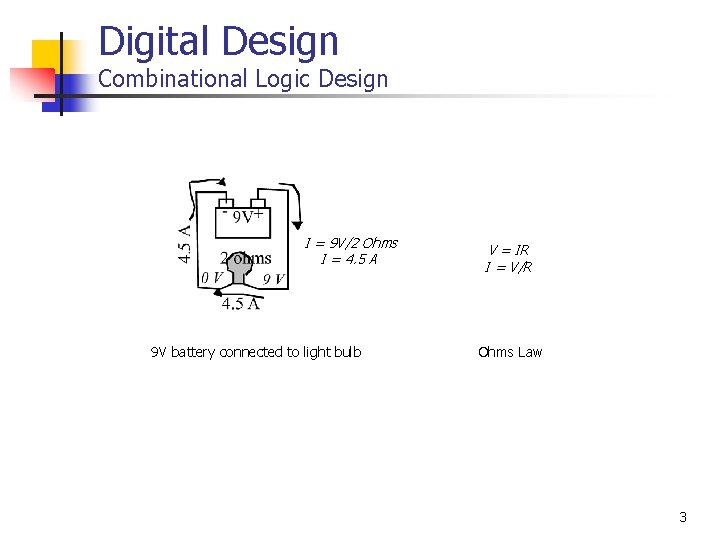
Digital Design Combinational Logic Design I = 9 V/2 Ohms I = 4. 5 A 9 V battery connected to light bulb V = IR I = V/R Ohms Law 3

Digital Design Combinational Logic Design The evolution of switches: • Relays (1930 s) • Vacuum tubes (1940 s) • Discrete transistors (1950 s) • Integrated circuit (IC) containing transistors (1960 s--present). IC’s originally held about ten transistors; now they can hold almost one billion. 4

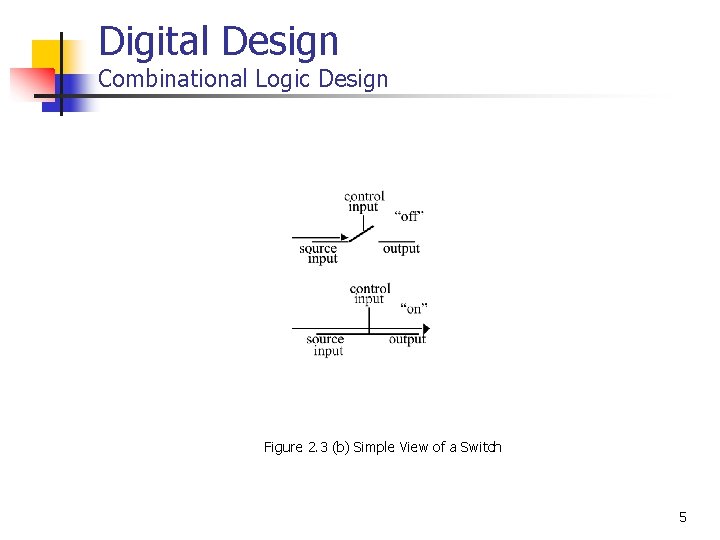
Digital Design Combinational Logic Design Figure 2. 3 (b) Simple View of a Switch 5

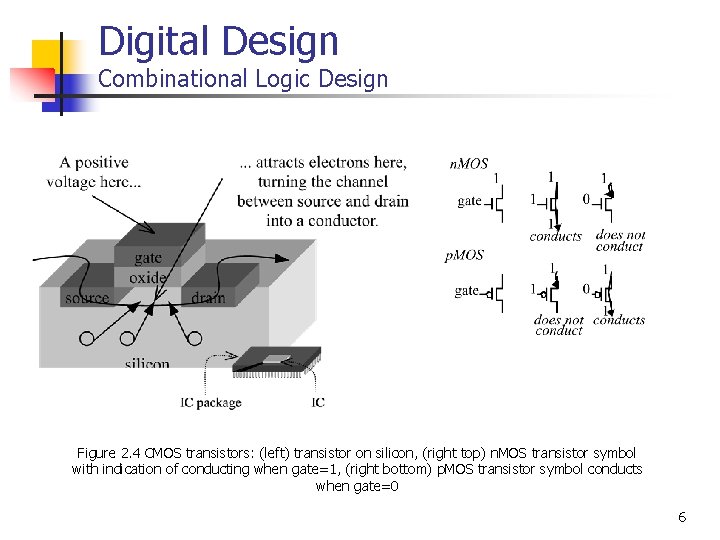
Digital Design Combinational Logic Design Figure 2. 4 CMOS transistors: (left) transistor on silicon, (right top) n. MOS transistor symbol with indication of conducting when gate=1, (right bottom) p. MOS transistor symbol conducts when gate=0 6

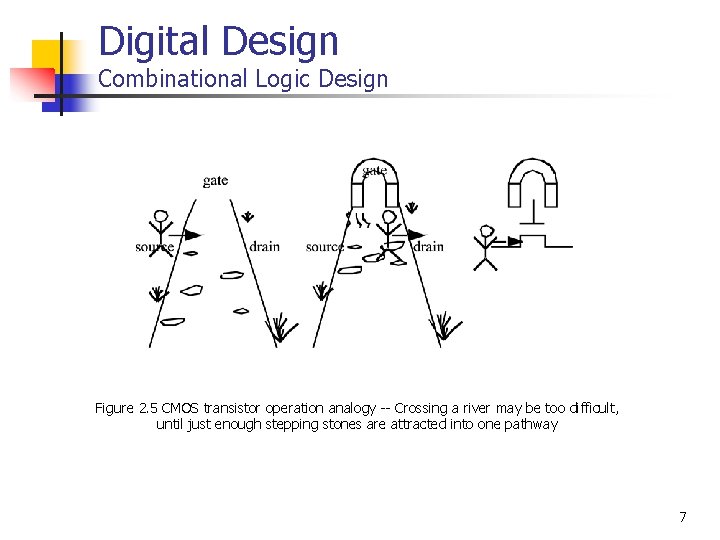
Digital Design Combinational Logic Design Figure 2. 5 CMOS transistor operation analogy -- Crossing a river may be too difficult, until just enough stepping stones are attracted into one pathway 7

Digital Design Combinational Logic Design Figure 2. 6 Having the right building blocks can make all the difference when building things. 8

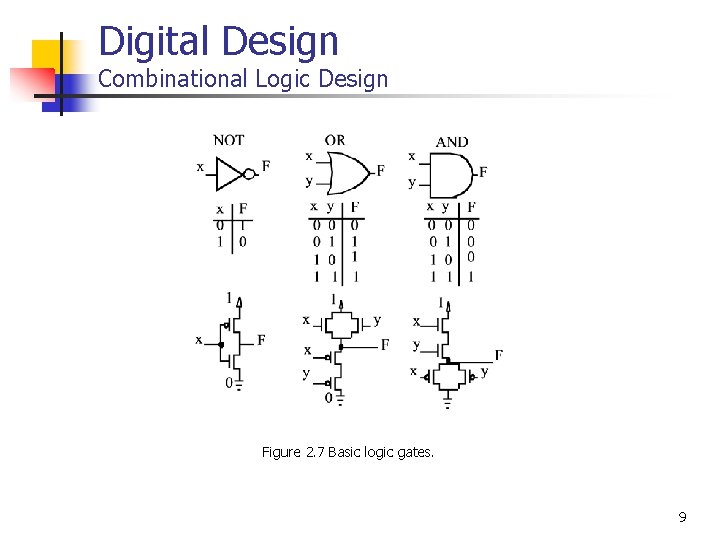
Digital Design Combinational Logic Design Figure 2. 7 Basic logic gates. 9

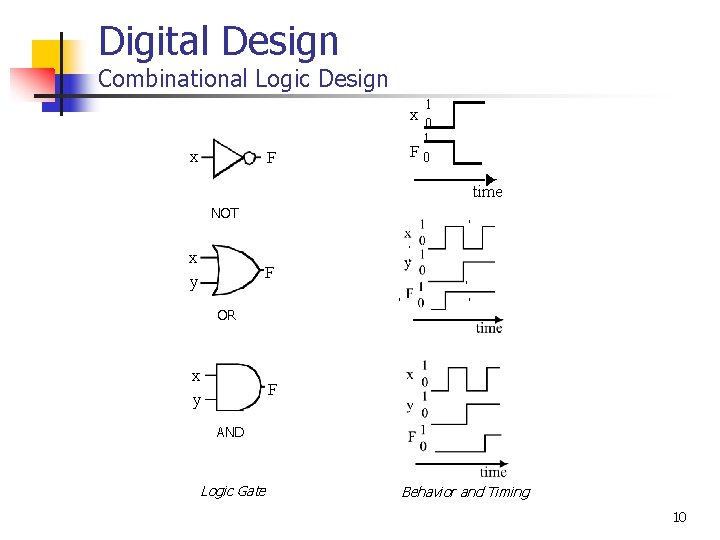
Digital Design Combinational Logic Design 1 x 0 x F 1 F 0 time NOT x y F OR x y F AND Logic Gate Behavior and Timing 10

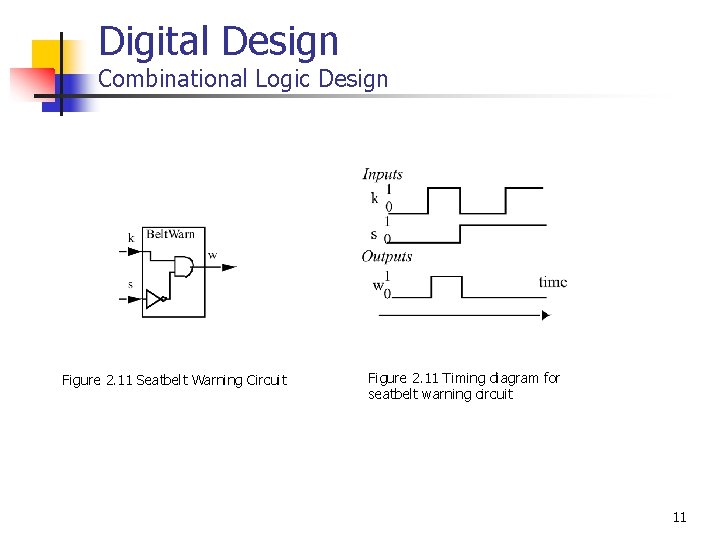
Digital Design Combinational Logic Design Figure 2. 11 Seatbelt Warning Circuit Figure 2. 11 Timing diagram for seatbelt warning circuit 11

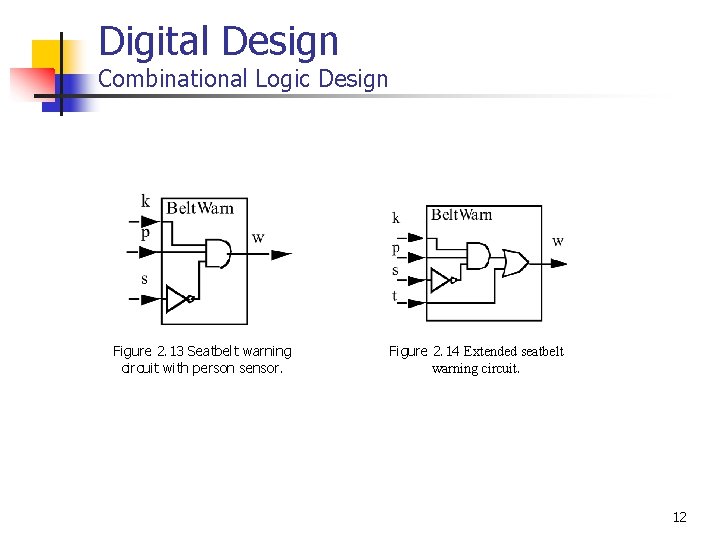
Digital Design Combinational Logic Design Figure 2. 13 Seatbelt warning circuit with person sensor. Figure 2. 14 Extended seatbelt warning circuit. 12

Digital Design Combinational Logic Design Commutative: a + b = b + a a * b = b * a Distributive a*(b + c) = a*b + a*c a+(b * c) = (a+b) * (a+c) Associative (a + b) + c = a + (b + c) (a * b) * c = a * (b * c) Identity 0 + a = a + 0 = a 1 * a = a * 1 = a Complement a + a’ = 1 a * a’ = 0 Boolean Algebra – Basic Properties 13

Digital Design Combinational Logic Design Null elements a + 1 = 1 a * 0 = 0 Idempotent Law a + a = a a * a = a Involution Law (a’)’ = a De. Morgan’s Law (a + b)’ = a’b’ (ab)’ = a’ + b’ Boolean Algebra – Additional Properties 14

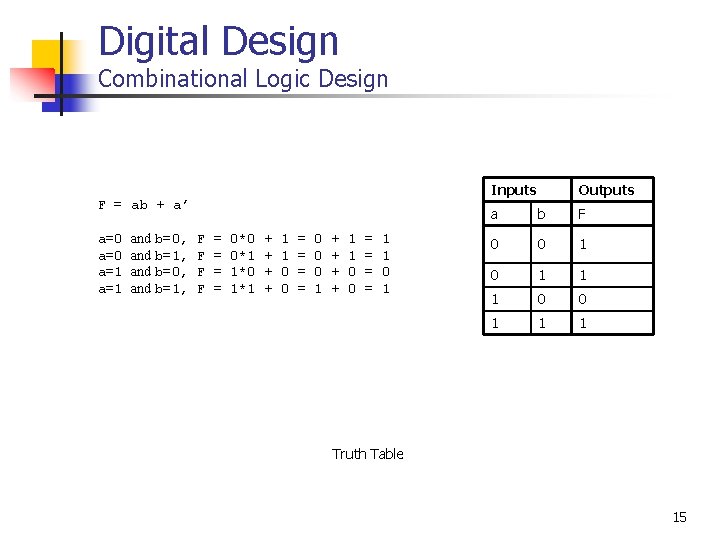
Digital Design Combinational Logic Design Inputs F = ab + a’ a=0 a=1 and b=0, and b=1, F F = = 0*0 0*1 1*0 1*1 + + 1 1 0 0 = = 0 0 0 1 + + 1 1 0 0 = = 1 1 0 1 Outputs a b F 0 0 1 1 1 Truth Table 15

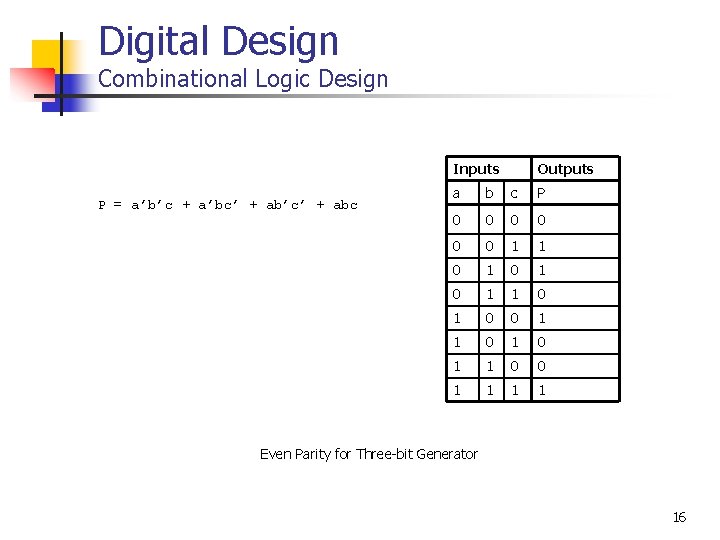
Digital Design Combinational Logic Design Inputs P = a’b’c + a’bc’ + ab’c’ + abc Outputs a b c P 0 0 0 1 1 0 1 0 1 0 0 1 1 0 0 1 1 Even Parity for Three-bit Generator 16

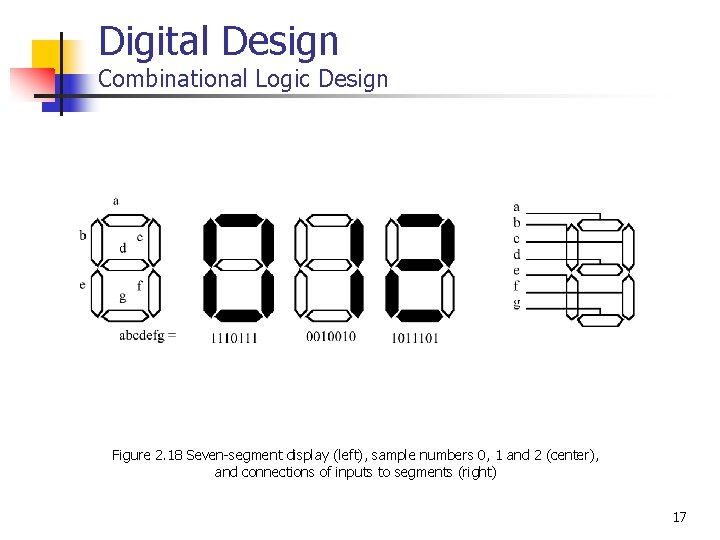
Digital Design Combinational Logic Design Figure 2. 18 Seven-segment display (left), sample numbers 0, 1 and 2 (center), and connections of inputs to segments (right) 17

Digital Design Combinational Logic Design Table 2. 2 4 -bit binary number to seven-segment display truth table 18

Digital Design Combinational Logic Design Process 19

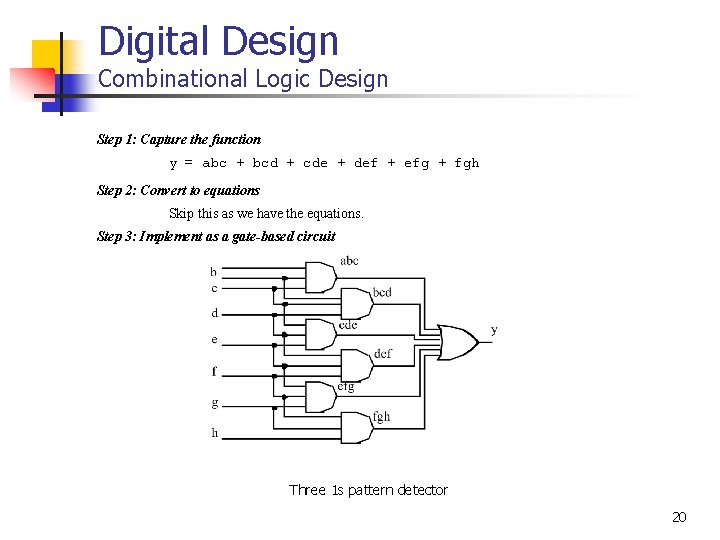
Digital Design Combinational Logic Design Step 1: Capture the function y = abc + bcd + cde + def + efg + fgh Step 2: Convert to equations Skip this as we have the equations. Step 3: Implement as a gate-based circuit Three 1 s pattern detector 20

Digital Design Combinational Logic Design Step 1: Capture the function Step 2: Convert to equations y = a’bc + ab’c + abc’ + abc z = a’b’c + a’bc’ + ab’c’ + abc Number-of-1 s counter gate-based circuit 21

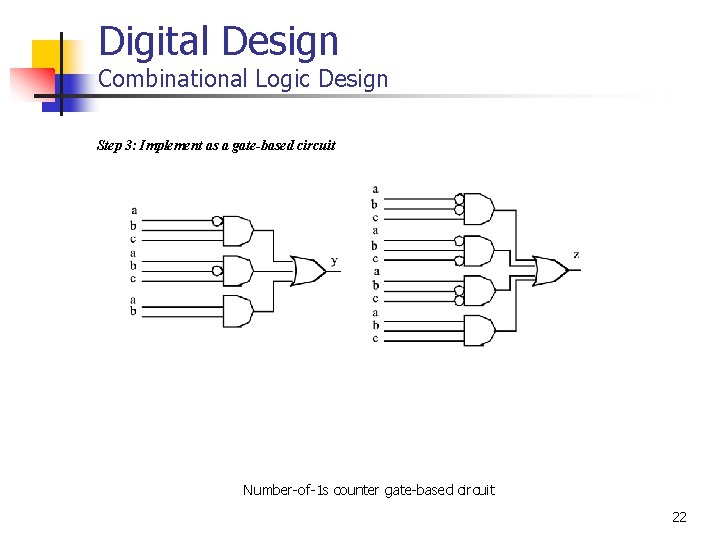
Digital Design Combinational Logic Design Step 3: Implement as a gate-based circuit Number-of-1 s counter gate-based circuit 22

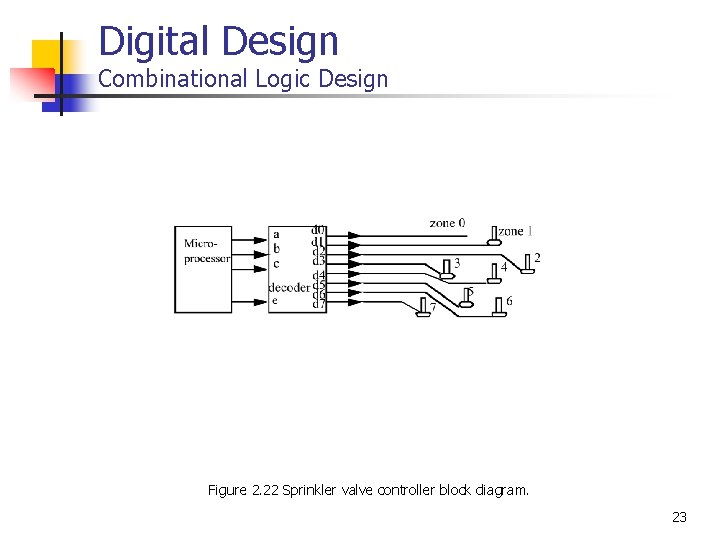
Digital Design Combinational Logic Design Figure 2. 22 Sprinkler valve controller block diagram. 23

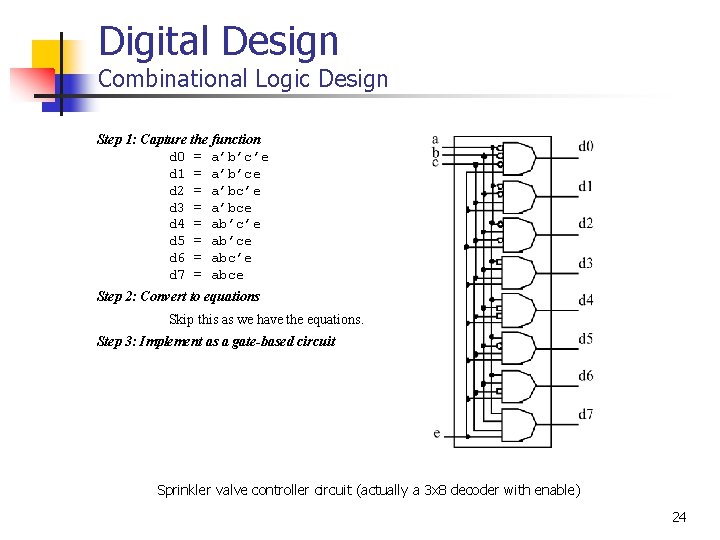
Digital Design Combinational Logic Design Step 1: Capture the function d 0 = a’b’c’e d 1 = a’b’ce d 2 = a’bc’e d 3 = a’bce d 4 = ab’c’e d 5 = ab’ce d 6 = abc’e d 7 = abce Step 2: Convert to equations Skip this as we have the equations. Step 3: Implement as a gate-based circuit Sprinkler valve controller circuit (actually a 3 x 8 decoder with enable) 24

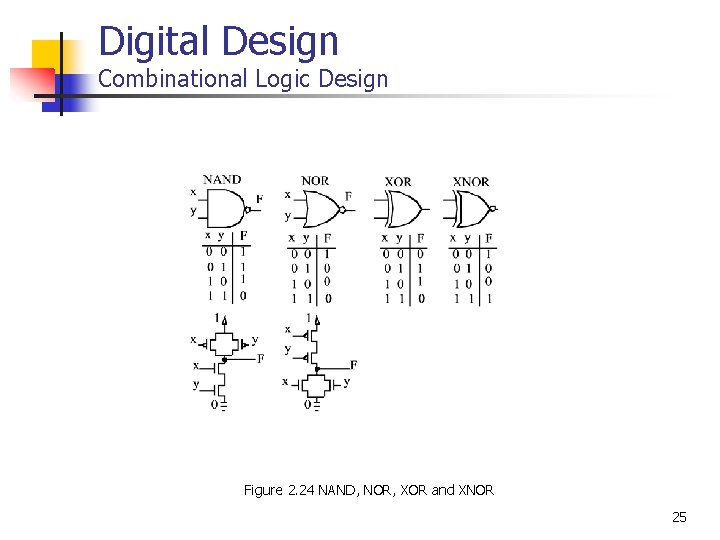
Digital Design Combinational Logic Design Figure 2. 24 NAND, NOR, XOR and XNOR 25

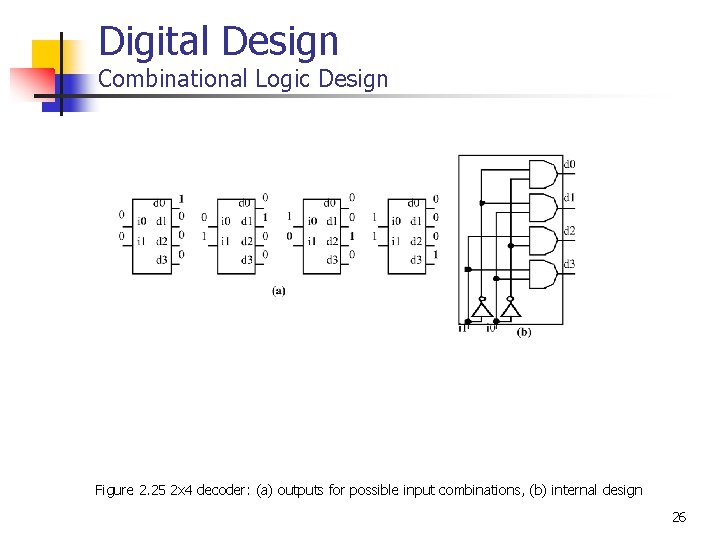
Digital Design Combinational Logic Design Figure 2. 25 2 x 4 decoder: (a) outputs for possible input combinations, (b) internal design 26

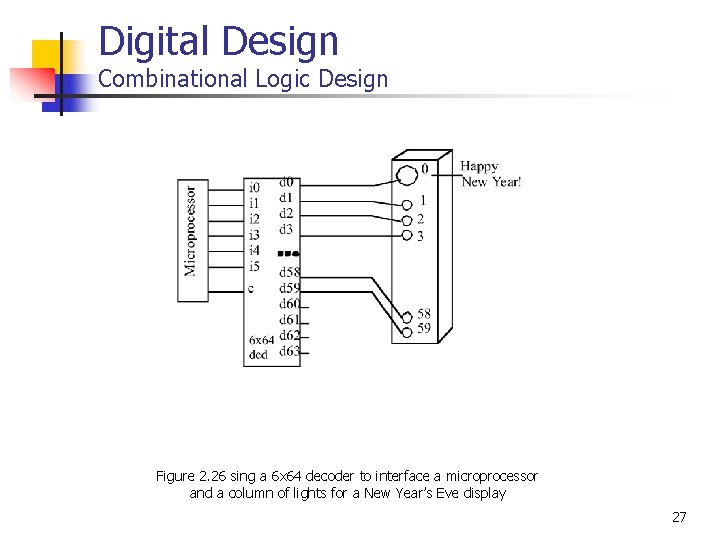
Digital Design Combinational Logic Design Figure 2. 26 sing a 6 x 64 decoder to interface a microprocessor and a column of lights for a New Year’s Eve display 27

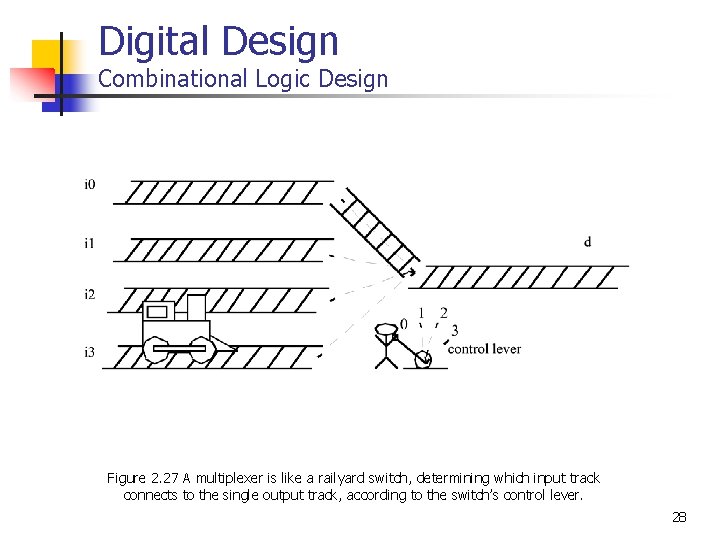
Digital Design Combinational Logic Design Figure 2. 27 A multiplexer is like a railyard switch, determining which input track connects to the single output track, according to the switch’s control lever. 28

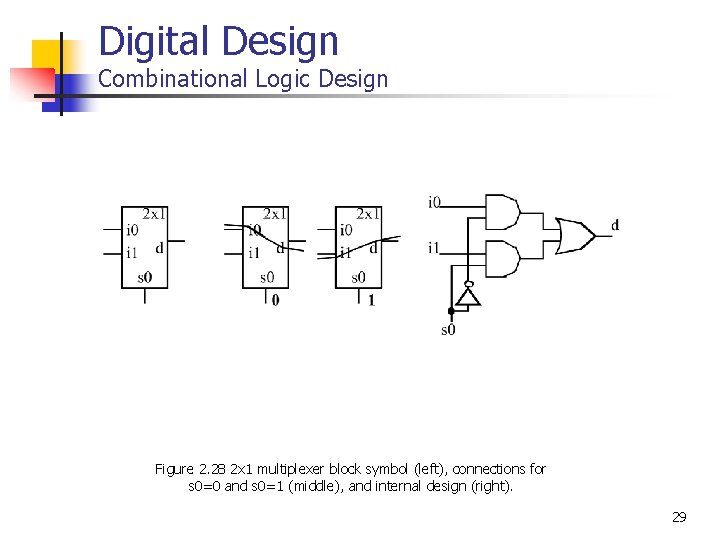
Digital Design Combinational Logic Design Figure 2. 28 2 x 1 multiplexer block symbol (left), connections for s 0=0 and s 0=1 (middle), and internal design (right). 29

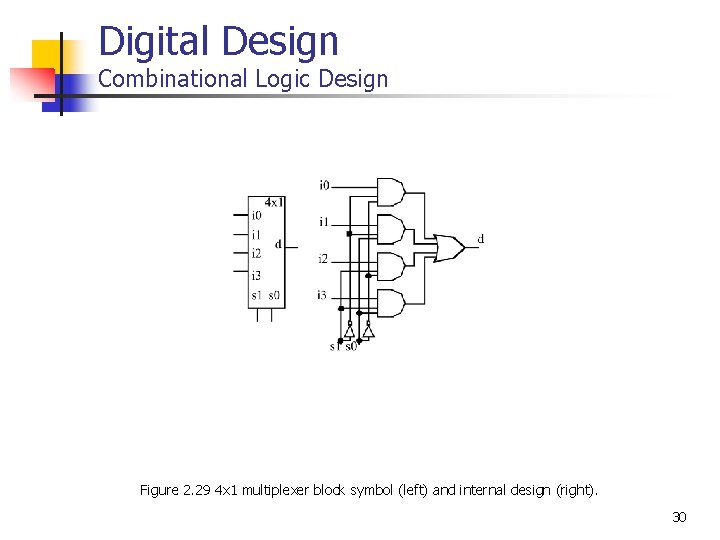
Digital Design Combinational Logic Design Figure 2. 29 4 x 1 multiplexer block symbol (left) and internal design (right). 30

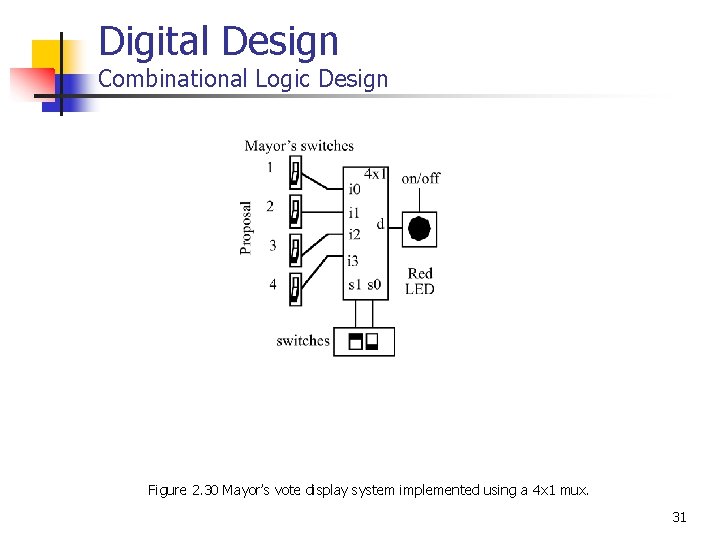
Digital Design Combinational Logic Design Figure 2. 30 Mayor’s vote display system implemented using a 4 x 1 mux. 31

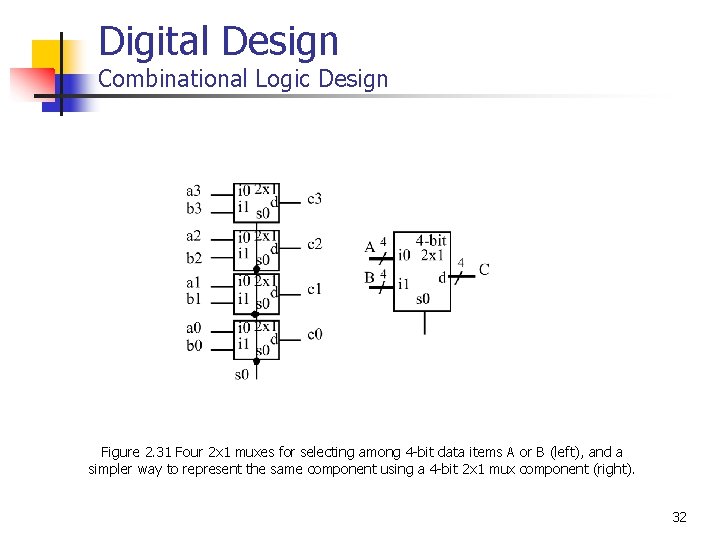
Digital Design Combinational Logic Design Figure 2. 31 Four 2 x 1 muxes for selecting among 4 -bit data items A or B (left), and a simpler way to represent the same component using a 4 -bit 2 x 1 mux component (right). 32

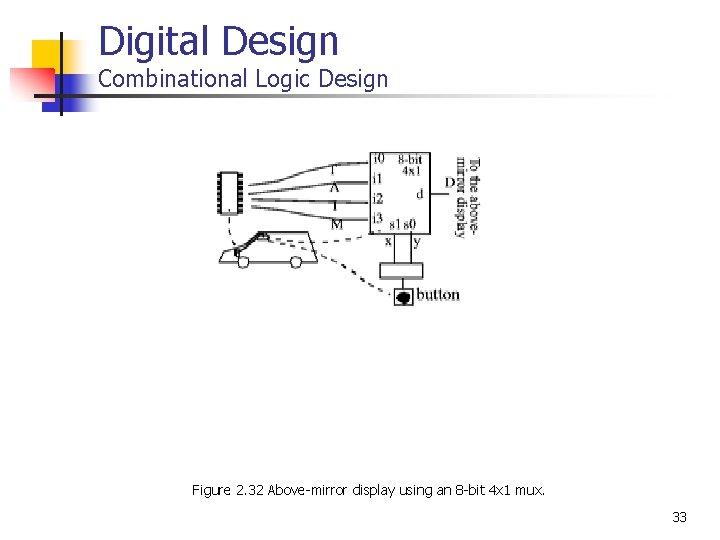
Digital Design Combinational Logic Design Figure 2. 32 Above-mirror display using an 8 -bit 4 x 1 mux. 33

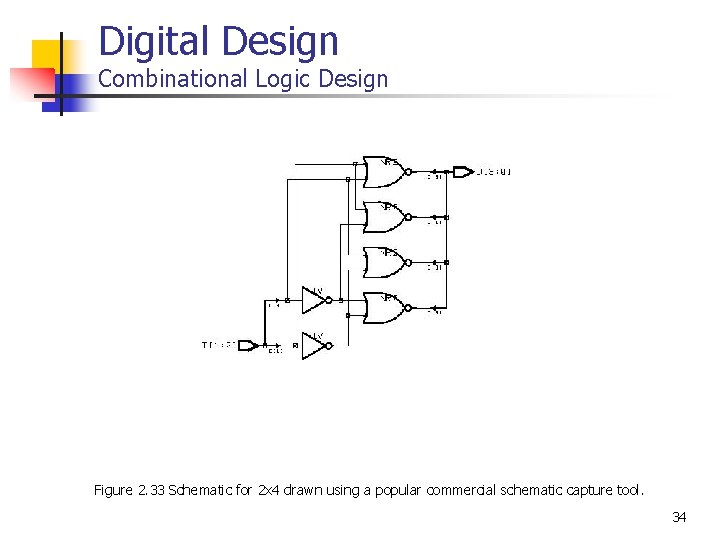
Digital Design Combinational Logic Design Figure 2. 33 Schematic for 2 x 4 drawn using a popular commercial schematic capture tool. 34

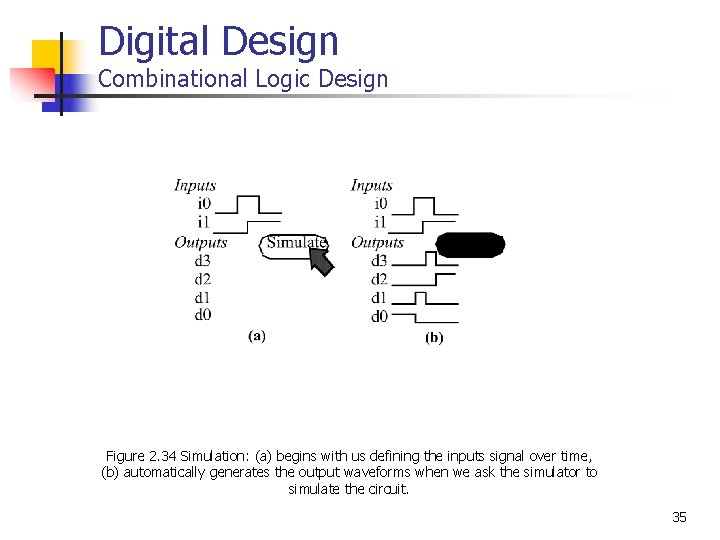
Digital Design Combinational Logic Design Figure 2. 34 Simulation: (a) begins with us defining the inputs signal over time, (b) automatically generates the output waveforms when we ask the simulator to simulate the circuit. 35

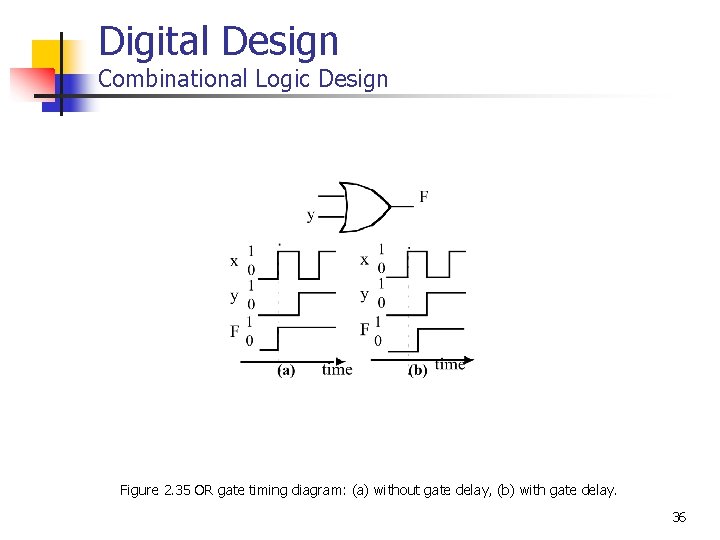
Digital Design Combinational Logic Design Figure 2. 35 OR gate timing diagram: (a) without gate delay, (b) with gate delay. 36