Digital Data How to Represent Numbers on a

Digital Data How to Represent Numbers on a Computer

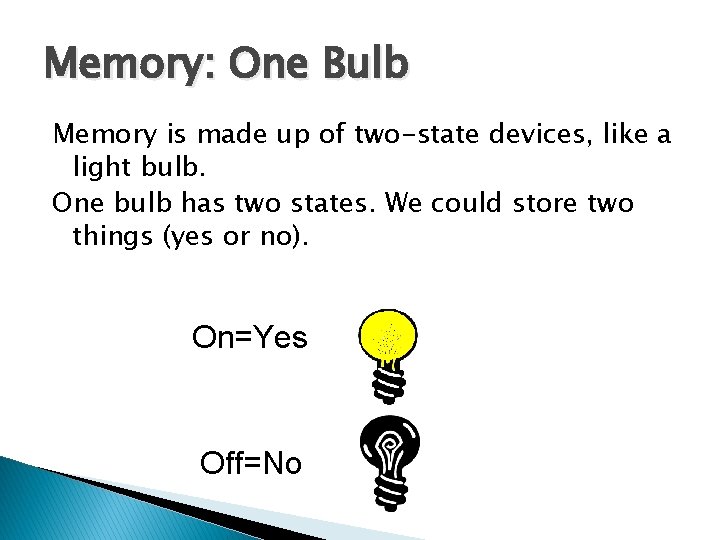
Memory: One Bulb Memory is made up of two-state devices, like a light bulb. One bulb has two states. We could store two things (yes or no). On=Yes Off=No

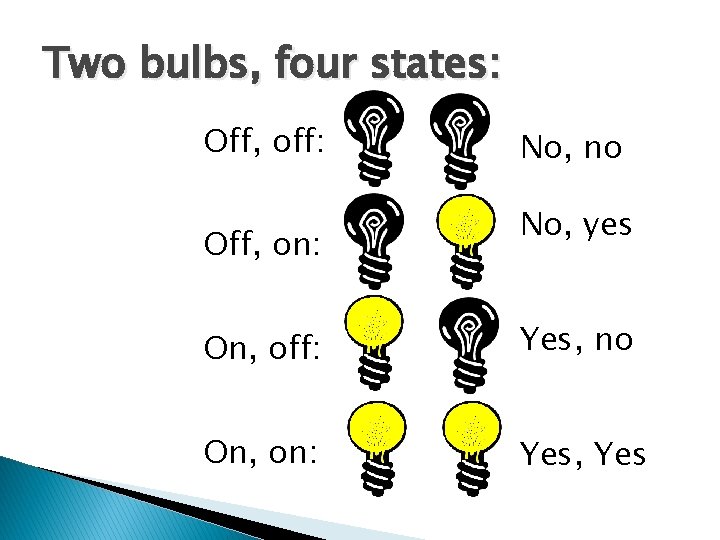
Two bulbs, four states: Off, off: Off, on: No, no No, yes On, off: Yes, no On, on: Yes, Yes

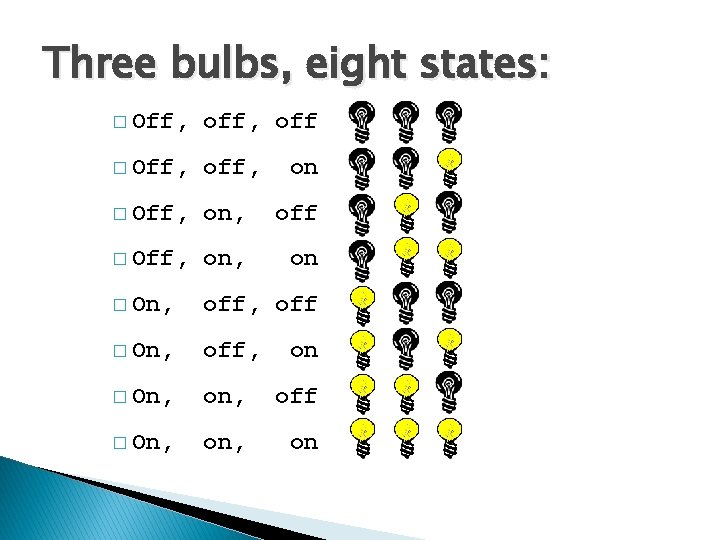
Three bulbs, eight states: � Off, off, off � Off, off, � Off, on, off � Off, on � On, off, off � On, off, � On, off � On, on on on

Four bulbs, 16 states:

Pretend they are numbers, where off=0 and on=1: 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

How do we interpret the numbers? � Base 10 numbers: ◦ 10 digits: 0 through 9 ◦ Place value is based on powers of 10 ___ 105 ___ 104 100, 000 10, 000 ___ 103 ___ 102 ___ 101 ___ 100 1, 000 10 1

Base 10 1 105 2 104 100, 000 10, 000 So 123, 456 = 1 * 100, 000 = 2 * 10, 000 = 3 * 1, 000 = 4 * 100 = 5 * 10 = 6 * 1 = 3 103 4 102 1, 000 100, 000 20, 000 3, 000 400 50 6 123, 456 100 5 101 10 6. 100 1

With 2 digits: � Base 2 number system: ◦ 2 digits: 0 through 1 ◦ Place value is based on powers of 2 __ 27 __ 26 __ 25 __ 24 __ 23 128 64 32 16 8 __ 22 __ 21 4 2 __ 20 1

Base 2 1 __ 27 0 __ 26 1 __ 25 0 __ 24 1 __ 23 0 __ 22 1 __ 21 0 __ 20 128 64 32 16 8 4 2 1 So 1010= 1 0 1 0 * * * * 128 64 32 16 8 4 2 1 = = = = 128 0 32 0 8 0 2 0 170

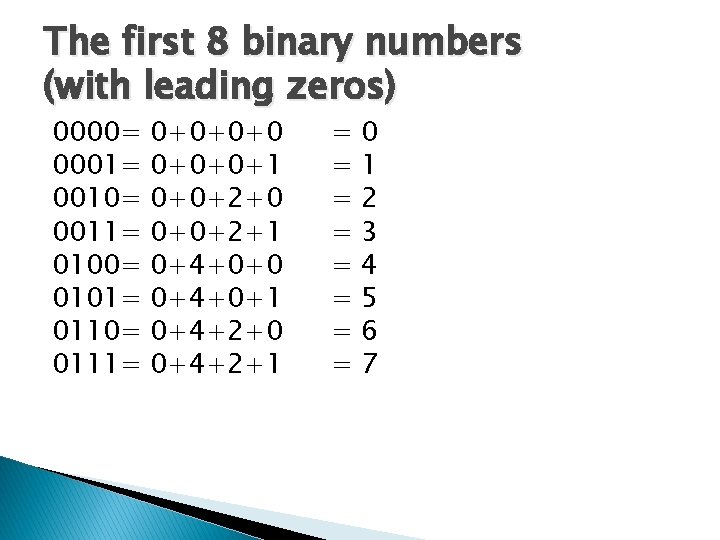
The first 8 binary numbers (with leading zeros) 0000= 0001= 0010= 0011= 0100= 0101= 0110= 0111= 0+0+0+0+1 0+0+2+0 0+0+2+1 0+4+0+0 0+4+0+1 0+4+2+0 0+4+2+1 = = = = 0 1 2 3 4 5 6 7

Binary numbers are represented in BYTES – groups of 8 bits Byte: a group of 8 bits. The basic unit of storage on most computers. 0 = 0000 1 = 0000 0001 2 = 0000 0010 3 = 0000 0011 4 = 0000 0100 5 = 0000 0101 6 = 0000 0110 7 = 0000 0111

Some other binary numbers 0000 = 0 0101 = 1 + 4 + 16 + 64 = 85 1000 0001 = 1 + 128 = 129 1111 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255

Need numbers greater than 255? Use two bytes: Smallest number = 0000 Biggest number = 1111 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + 512 + 1024 + 2048 + 4096 + 8192 + 16, 384 + 32, 768 = 65, 535

Need numbers greater than 65, 535? Use 4 bytes: Smallest number: 0000 0000 Biggest number: 1111 1111 = 4, 294, 967, 295

Other numbers � There also ways to represent: � These will be covered elsewhere. ◦ Decimal fractions ◦ Negative numbers

The End