Digital Control Systems zPlane Analysis of Discrete Time

Digital Control Systems z-Plane Analysis of Discrete Time Control Systems

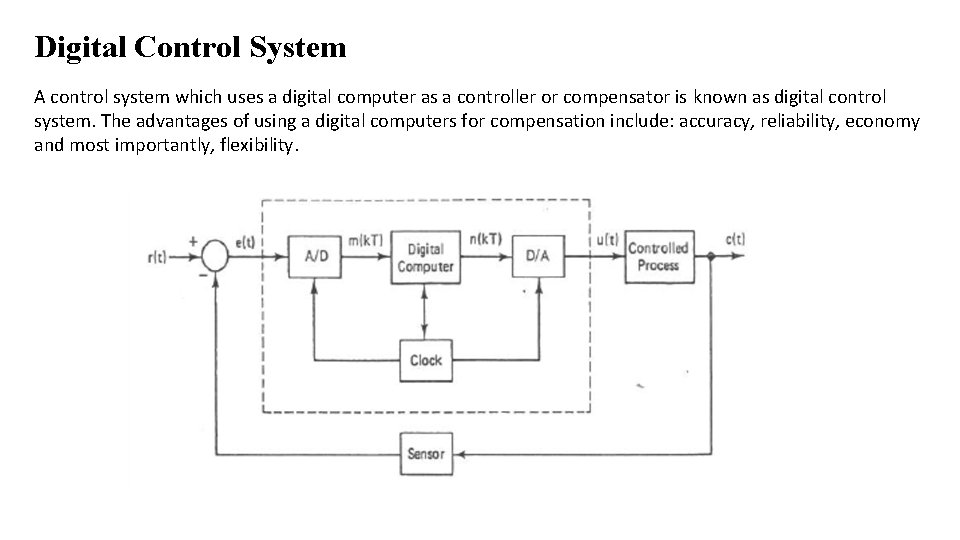
Digital Control System A control system which uses a digital computer as a controller or compensator is known as digital control system. The advantages of using a digital computers for compensation include: accuracy, reliability, economy and most importantly, flexibility.

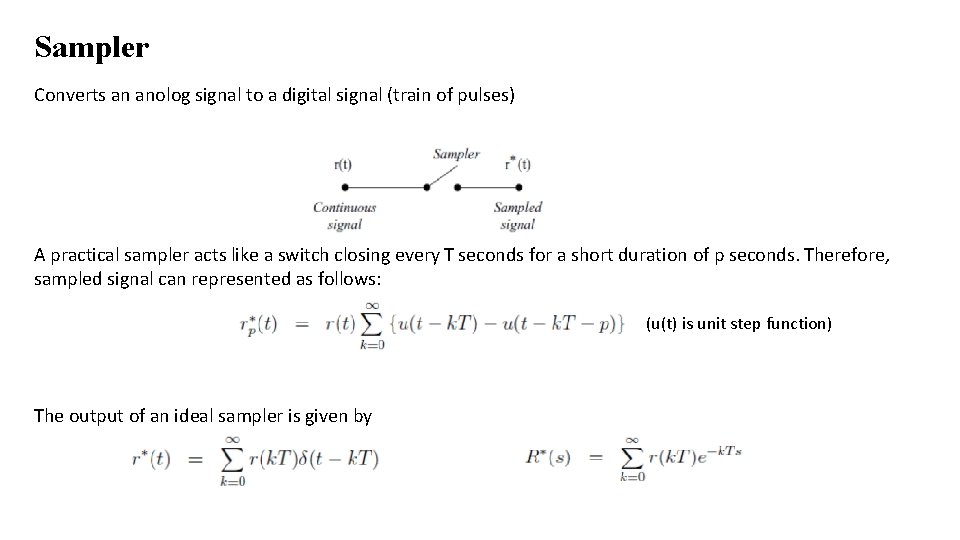
Sampler Converts an anolog signal to a digital signal (train of pulses) A practical sampler acts like a switch closing every T seconds for a short duration of p seconds. Therefore, sampled signal can represented as follows: (u(t) is unit step function) The output of an ideal sampler is given by

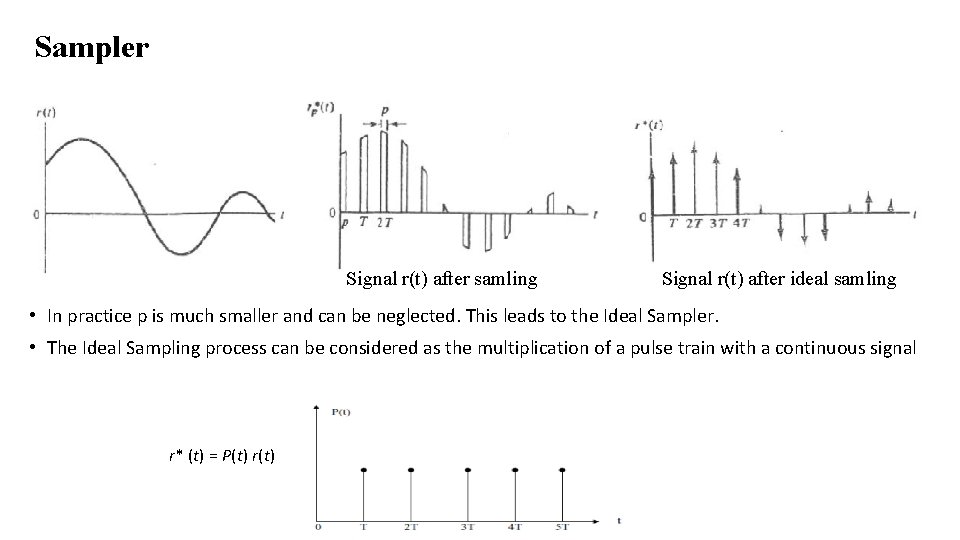
Sampler Signal r(t) after samling Signal r(t) after ideal samling • In practice p is much smaller and can be neglected. This leads to the Ideal Sampler. • The Ideal Sampling process can be considered as the multiplication of a pulse train with a continuous signal r* (t) = P(t) r(t)

Sampler r(t) = 0, for t < 0

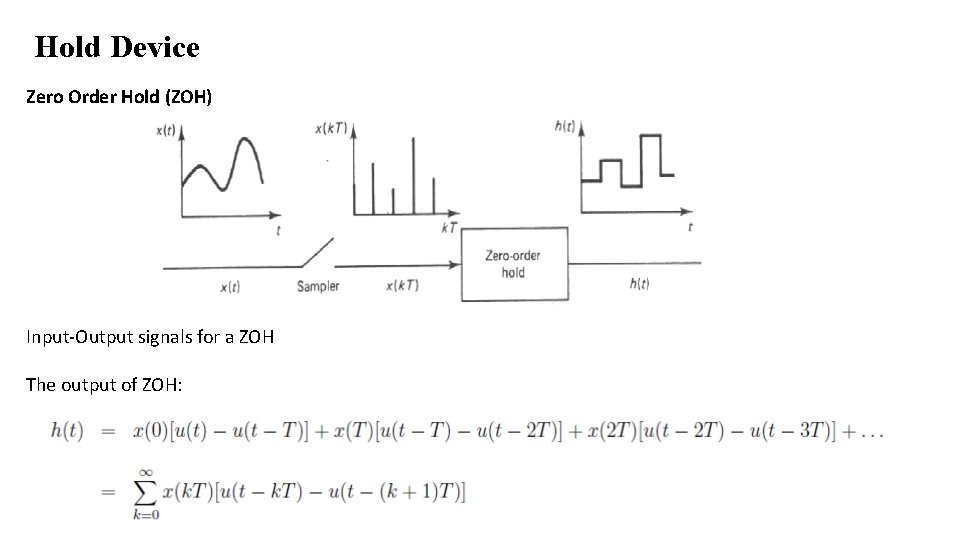
Hold Device • The hold device is called n-th order hold if it uses an n-th order polynomial extrapolator. n=1 first order hold n=0 zero order hold

Hold Device Zero Order Hold (ZOH) Input-Output signals for a ZOH The output of ZOH:

Hold Device Zero Order Hold (ZOH) The output of ZOH: We know from Laplace transforms that ZOH Transfer function

Hold Device Zero Order Hold (ZOH) Suppose the transfer function G(s) follows the ZOH. Then the product of ZOH and G(s) becomes: Obtain the z transform of X(s): Let

Hold Device Zero Order Hold (ZOH)

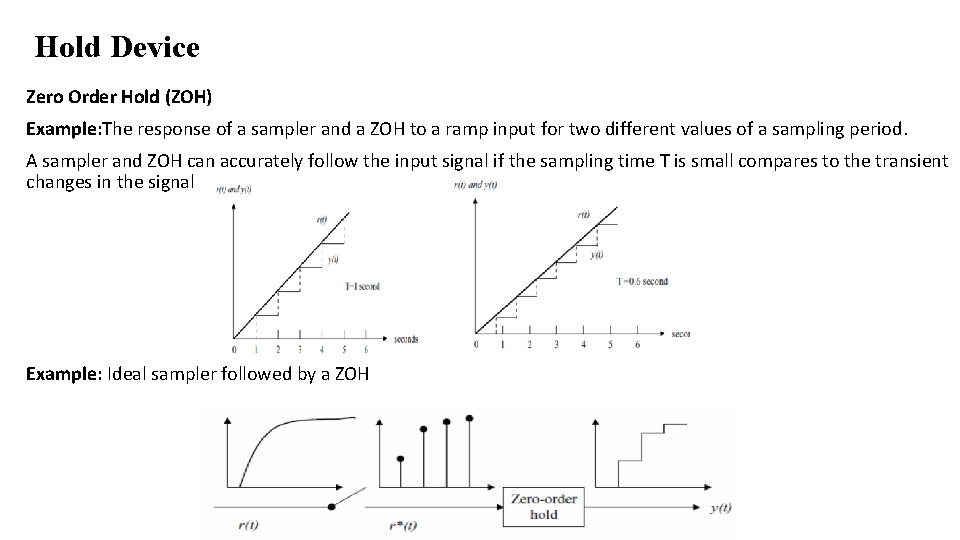
Hold Device Zero Order Hold (ZOH) Example: The response of a sampler and a ZOH to a ramp input for two different values of a sampling period. A sampler and ZOH can accurately follow the input signal if the sampling time T is small compares to the transient changes in the signal Example: Ideal sampler followed by a ZOH

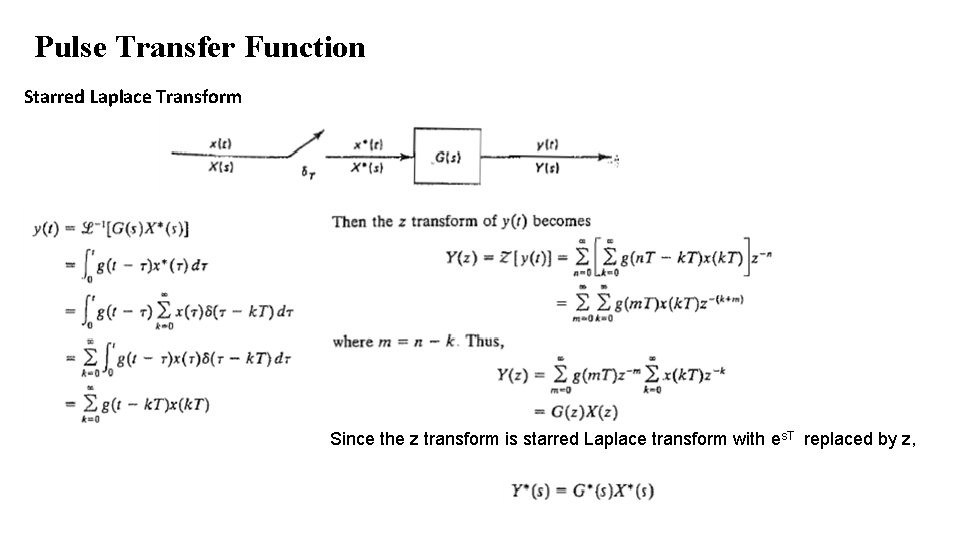
Pulse Transfer Function Transfer function of a continuous time system relates the Laplace transform of the continuous-time output to that of the continuous time input. Pulse transfer function relates the z-transform of the output at the sampling instants to that of the sampled input. Starred Laplace Transform Assumption: Zero initial conditions. • While taking the starred Laplace tranform of a product of transforms, where some are ordinary Laplace transforms and others are starred Laplace transform, the functions already in starred Laplace transforms can be factored out of the starred Laplace transform. • The output of a sampled-data system is continuous with respect to time. However the pulse transform (starred LT) of the output, Y (s) and z-transform of the output Y (z), gives the values of output y(t) only at sampling instants.

Pulse Transfer Function Starred Laplace Transform Since the z transform is starred Laplace transform with es. T replaced by z,

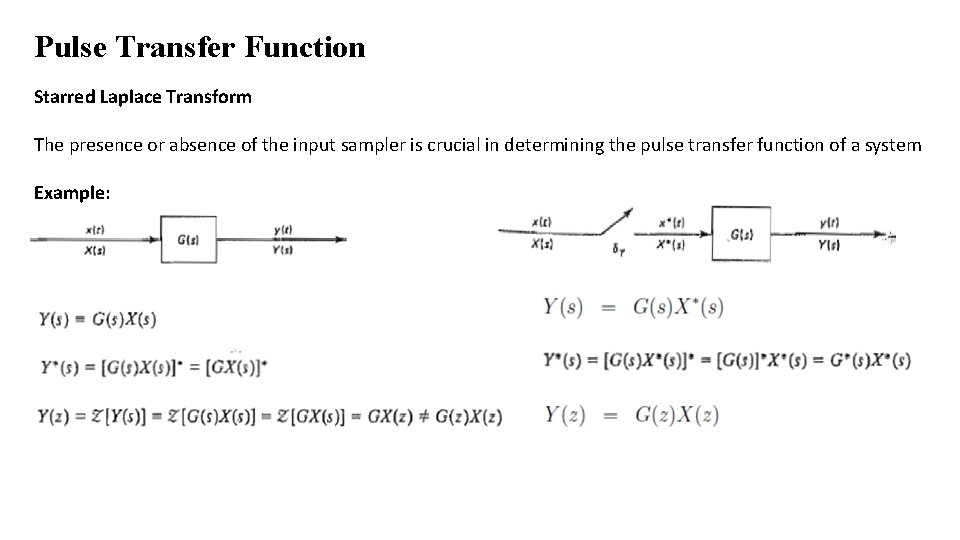
Pulse Transfer Function Starred Laplace Transform The presence or absence of the input sampler is crucial in determining the pulse transfer function of a system Example:

Pulse Transfer Function Pulse transfer function of cascaded elements Taking starred Laplace transforms on both sides of above equations

Pulse Transfer Function Pulse transfer function of cascaded elements where

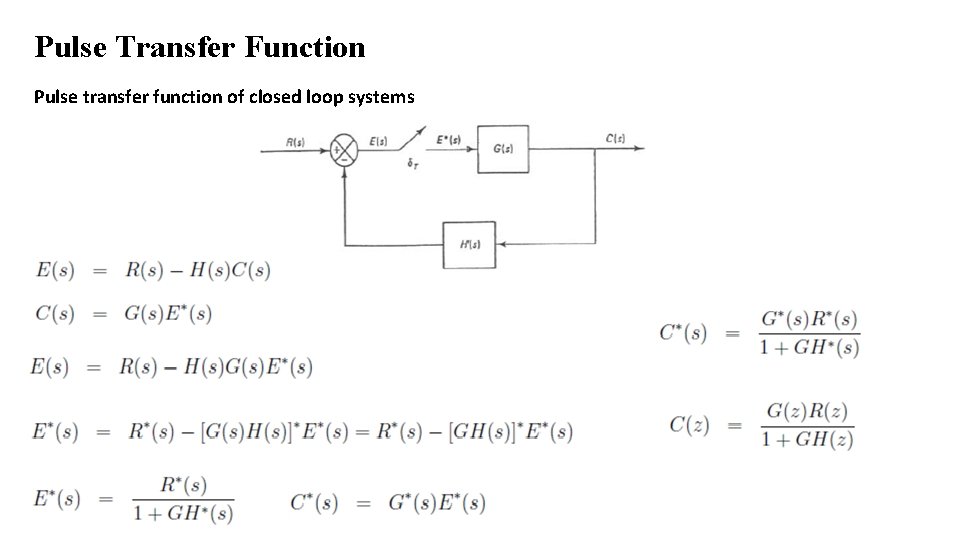
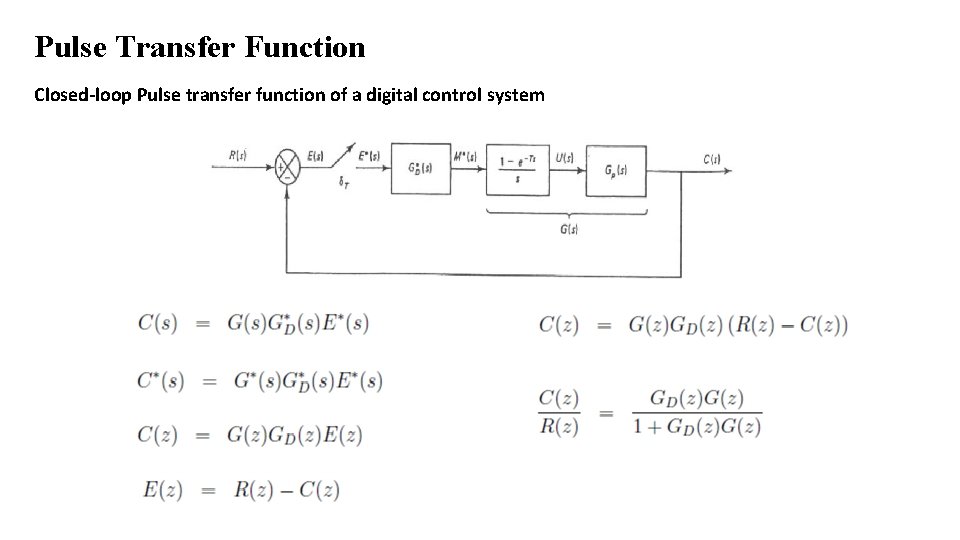
Pulse Transfer Function Pulse transfer function of closed loop systems

Pulse Transfer Function Example:

Pulse Transfer Function Pulse transfer function of a digital controller Pulse tranfer function of a digital controller can be easily obtained from its input-ouput characteristic which is specified by means of difference equation: where m(k) and e(k) are the output and input signals respectively. Taking z-transforms and simplifying we get the pulse transfer function of the digital controller:

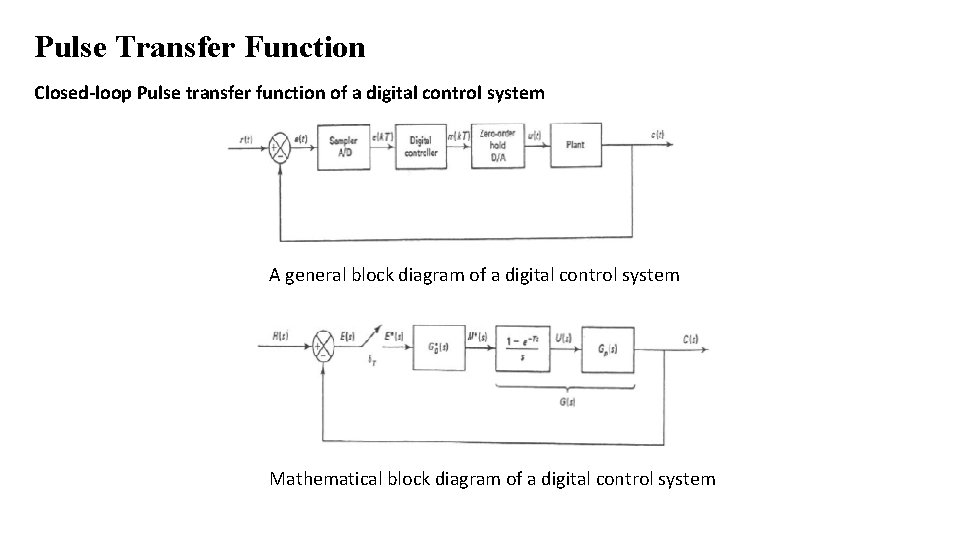
Pulse Transfer Function Closed-loop Pulse transfer function of a digital control system A general block diagram of a digital control system Mathematical block diagram of a digital control system

Pulse Transfer Function Closed-loop Pulse transfer function of a digital control system

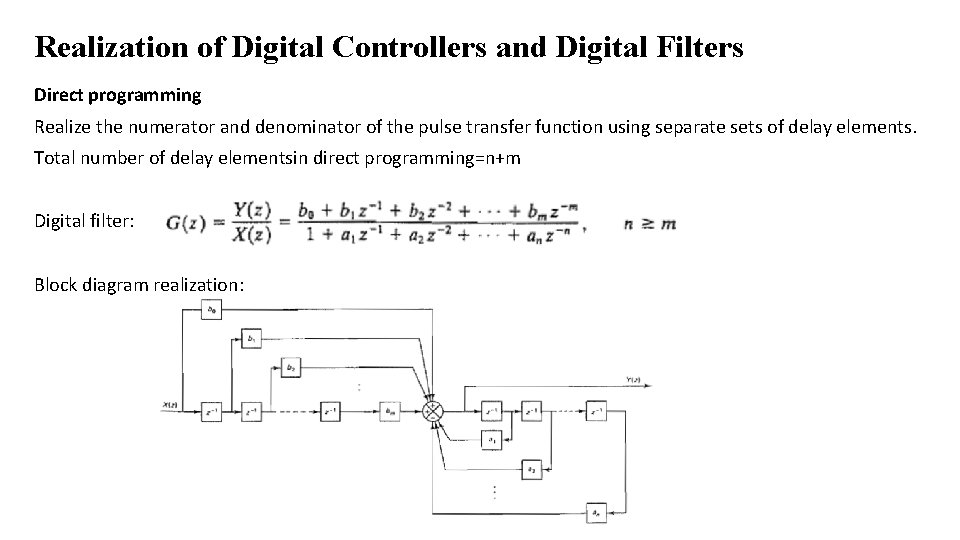
Realization of Digital Controllers and Digital Filters The general form of the pulse transfer function between the output Y(z) and X(z) is given by • Direct programming • Standart programming In these programmings, coefficients appear as multipliers in the block diagram realization. Those block diagram schemes where the coefficients appear directly as multipliers are called direct structures.

Realization of Digital Controllers and Digital Filters Direct programming Realize the numerator and denominator of the pulse transfer function using separate sets of delay elements. Total number of delay elementsin direct programming=n+m Digital filter: Block diagram realization:

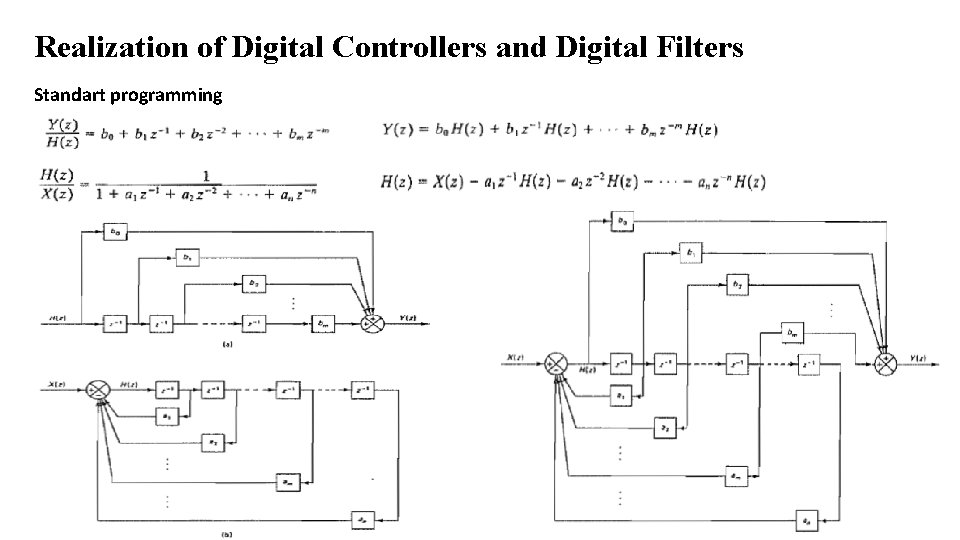
Realization of Digital Controllers and Digital Filters Standart programming The number of delay elements required in direct programming can be reduced. The number of delay elements used in realizing the pulse transfer function can be reduced from n+m to n (where n≥m) by rearranging the block diagram.

Realization of Digital Controllers and Digital Filters Standart programming