Digital Control Systems State Space Analysis1 INTRODUCTION INTRODUCTION

Digital Control Systems State Space Analysis(1)

INTRODUCTION •

INTRODUCTION State space: The n-dimensional space whose coordinate axes consist of the x 1 -axis, x 2 -axis, . . xn-axis is called a state space. State-space equations: In state-space analysis, we are concerned with three types of variables that are involved in the modeling of dynamic systems: input variables, output variables, and state variables. For Linear or Nonlinear discrete-time systems:

INTRODUCTION For Linear Time-varying discrete-time systems:

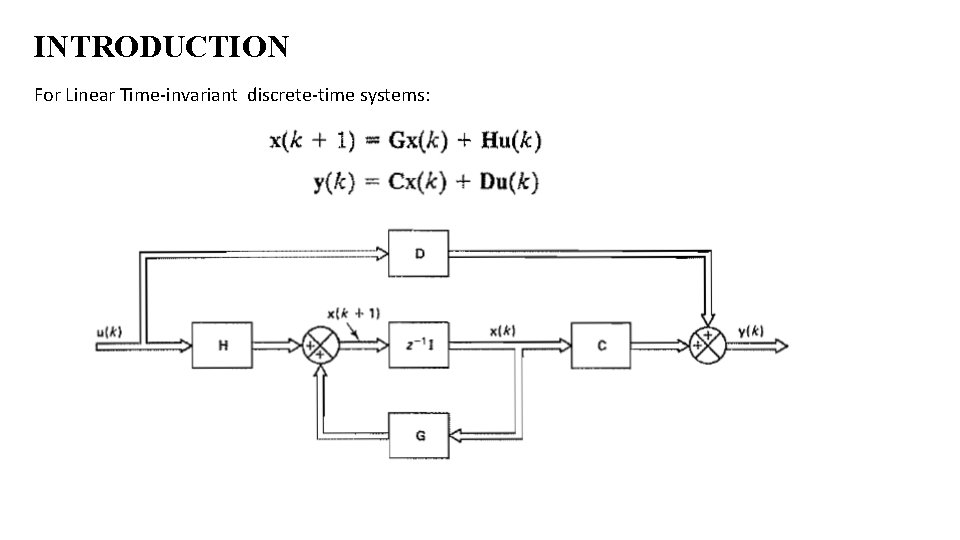
INTRODUCTION For Linear Time-invariant discrete-time systems:

INTRODUCTION For Linear or Nonlinear continuous-time systems: For Linear Time-varying continuous time systems:

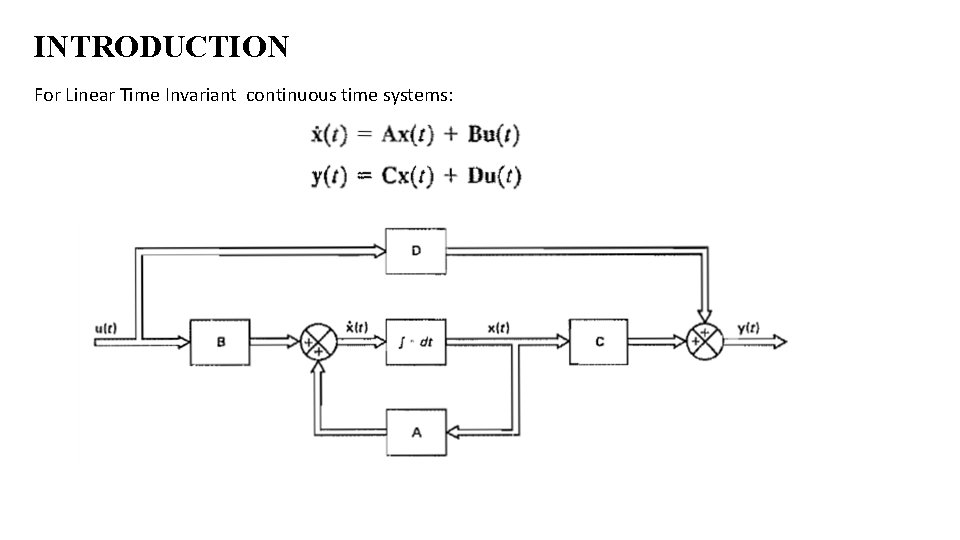
INTRODUCTION For Linear Time Invariant continuous time systems:

STATE SPACE REPRESENTATIONS OF DISCRETE TIME SYSTEMS Canonical Forms for Discrete Time State Space Equations or There are many ways to realize state-space representations for the discrete time system represented by these equations:

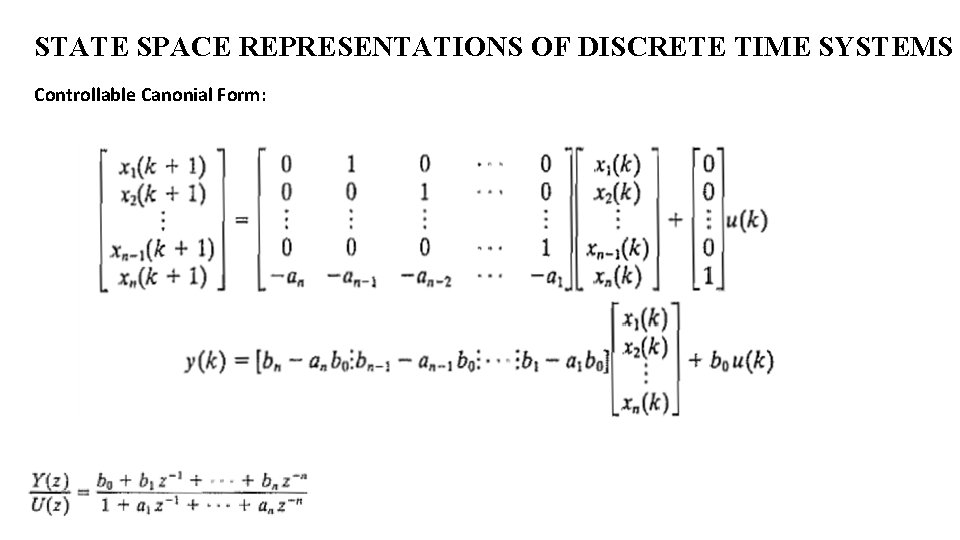
STATE SPACE REPRESENTATIONS OF DISCRETE TIME SYSTEMS Controllable Canonial Form:

STATE SPACE REPRESENTATIONS OF DISCRETE TIME SYSTEMS Controllable Canonical Form: If we reverse the order of the state variables:

STATE SPACE REPRESENTATIONS OF DISCRETE TIME SYSTEMS Observable Canonical Form

STATE SPACE REPRESENTATIONS OF DISCRETE TIME SYSTEMS Observable Canonical Form: If we reverse the order of the state variables:

STATE SPACE REPRESENTATIONS OF DISCRETE TIME SYSTEMS Diagonal Canonical Form: If the poles of pulse transfer function are all distinct, then the state-space representation may be put in the diagonal canonical form as follows:

STATE SPACE REPRESENTATIONS OF DISCRETE TIME SYSTEMS Jordan Canonical Form: If the poles of pulse transfer function involves a multiple pole of orde m at z=p 1 and all other poles are distinct:

STATE SPACE REPRESENTATIONS OF DISCRETE TIME SYSTEMS Example:

STATE SPACE REPRESENTATIONS OF DISCRETE TIME SYSTEMS Example:

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Rank of a Matrix A matrix A is called of rank m if the maximum number of linearly independent rows (or columns) is m. Properties of Rank of a Matrix

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Properties of Rank of a Matrix (cntd. )

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Eigenvalues of a Square Matrix

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Eigenvalues of a Square Matrix The n roots of the characteristic equation are called eigenvalues of A. They are also called the characteristic roots. • An n×n real matrix A does not necessarily possess real eigenvalues. • Since the characteristic equation is a polynomial with real coefficients, any compex eigenvalues must ocur in conjugate pairs. • If we assume the eigenvalues of A to be λi and those of to be μi then μi = (λi)-1

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Eigenvectors of an n×n Matrix Similar Matrices

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Diagonalization of Matrices

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Jordan Canonical Form

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Jordan Canonical Form

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Jordan Canonical Form : only one eigenvector : two linearly independent eigenvectors : three linearly independent eignvectors

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Jordan Canonical Form

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Similarity Transformation When an n×n Matrix has Distinct Eigenvalues

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Similarity Transformation When an n×n Matrix has Distinct Eigenvalues

EIGENVALUES, EIGENVECTORSAND SIMILARITY TRANSF. Similarity Transformation When an n×n Matrix Has Multiple Eigenvalues

STATE SPACE REPRESENTATIONS OF DISCRETE TIME SYSTEMS Nonuniqueness of State Space Representations: For a given pulse transfer function syste the state space representation is not unique. The state equations, however, are related to each other by the similarity transformation. 1 Let us define a new state vector by 2 where P is a nonsingular matrix. By substituting to 2 1

STATE SPACE REPRESENTATIONS OF DISCRETE TIME SYSTEMS Nonuniqueness of State Space Representations: Let us define then ≡ Since matrix P can be any nonsingular nn matrix, there are infinetely many state space representations for a given system. If we choose P properly: (If diagonalization is not possible)