Digital Communications Lecture 12 Channel Capacity Bandpass Signal

Digital Communications Lecture # 12 Channel Capacity & Bandpass Signal Representation Sidra Shaheen Syed Sidra. shaheen@iqraisb. edu. pk

Topical Overview • Channel Coding Theorem • Bandpass Signal Representation

Channel Capacity

Channel Capacity for Discrete Channels

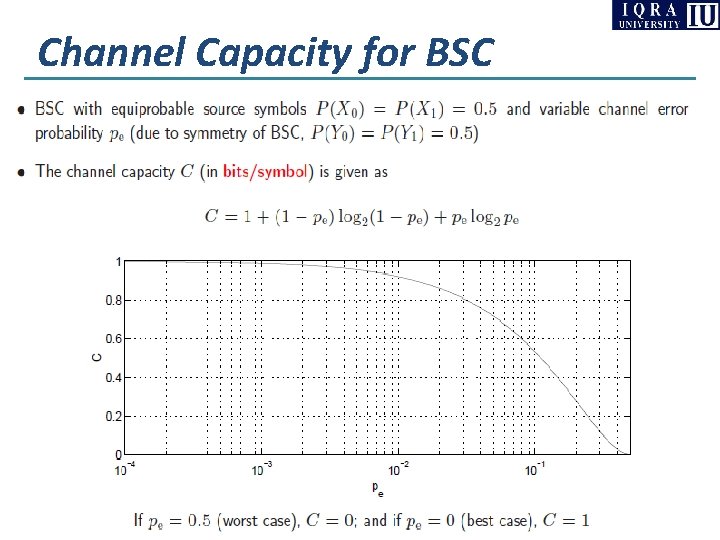
Channel Capacity for BSC

Channel Capacity for BSC (derivation)

Channel Capacity and Channel Coding

Digital Communication System • Source Encoding: Removes the redundant information embedded in the message signal, therefore represents the message with as few binary digits as possible, i. e. , data compression • Channel Encoding: Introduces redundancy in a “controlled” manner which can be used at the receiver to overcome the effects of noise, interference and fading. Provides “noise immunity” to transmitted information. • Modulation: Converts (maps) codewords to high-frequency analog waveforms. A certain parameter of the carrier signal (i. e. , modulated signal) is varied in accordance with message signal (i. e. modulating signal) e. g. amplitude shift keying (ASK), phase shift keying (PSK), frequency shift keying (FSK) • Receiver Blocks: Perform the inverse of the transmitter operations in order to recover the original analog message (continuous-time continuous-amplitude) signal. • In a practical digital communication receiver, there also additional sub-blocks such as channel estimation, synchronization (frame/frequency/phase), authentications, crypto, multiplexing, etc.

Why is Modulation Required? Modulation shifts the baseband signal to a higher frequency band, centered at the so-called “carrier frequency”. • To achieve easy radiation: Dimensions of the transmit/receive antennas are limited by the corresponding wavelength. The frequency conversion allows the use of practical antenna lengths. • To accommodate for simultaneous transmission of several baseband signals: Simultaneous transmission of different baseband signals which are possibly overlapping can be facilitated by assigning slightly different frequency carriers for each one. 9

Baseband Signal Representation 10

Baseband Signal Representation • Find |S+(f)|by deleting negative frequencies of |S(f)|& multiply result by 2 S+(f)= 2 u(f)S(f) s+(t) is known as the analytic signal or pre-envelope of s(t) • Find s(t) using IFT find signal whose Fourier transform = u-1(f) we know that F[u(t)] = by duality by convolution let = 2 u(f) s+(t) = then s(t) = 11

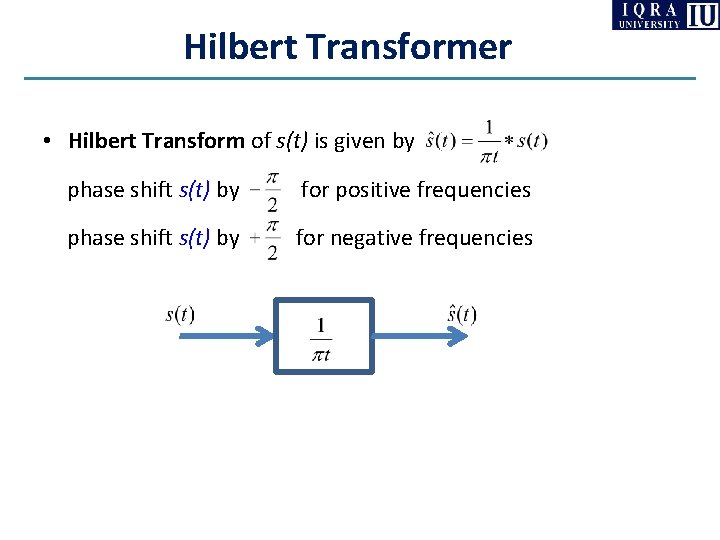
Hilbert Transformer • Hilbert Transform of s(t) is given by phase shift s(t) by for positive frequencies phase shift s(t) by for negative frequencies

Low-pass Equivalent Signal • sl(t) = low pass representation of s(t) • Determined by shifting spectrum of s+(t) left by fc S(f) Sl(f) = S+ (f + fc) = 2 u(f + fc)S(f + fc) sl(t) = s+(t) exp(-j 2πfct) A fc S+(f) fc f f 0 f 2 A sl(t) is a low pass signal • Sl(f) ≡ 0 for all | f | ≥ W s(t) Down Conversion Sl(f) 2 A sl(t) f 13

Low-pass Equivalent Signal sl(t) = s+(t)exp(-j 2πfct) sl(t) = x(t) + jy(t) 14

Upconversion As we know that s(t) Up Conversion sl(t) lowpass to bandpass transform describes relationship of s(t) in terms of x(t) & y(t) 15

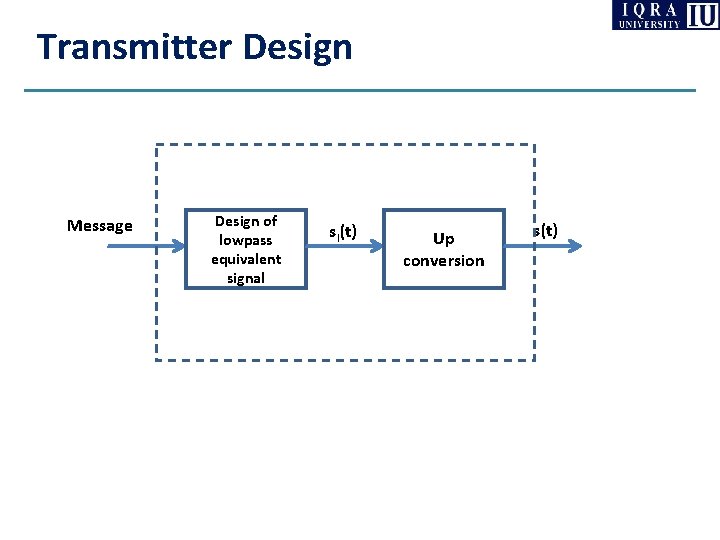
Transmitter Design Message Design of lowpass equivalent signal sl(t) Up conversion s(t)

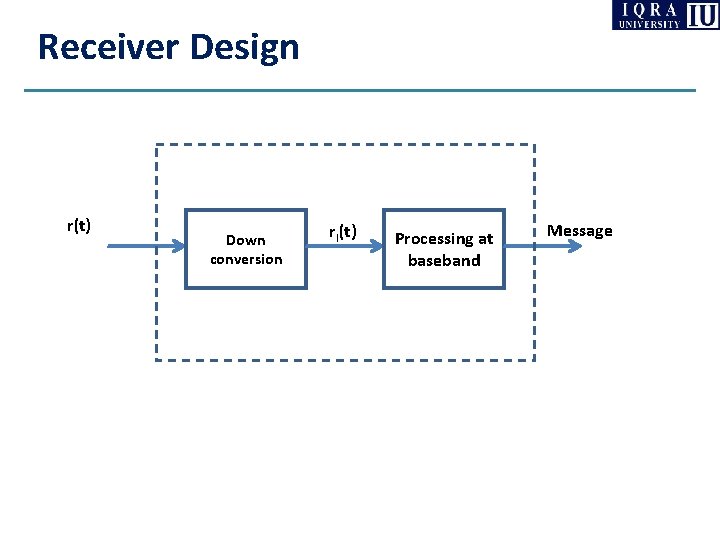
Receiver Design r(t) Down conversion rl(t) Processing at baseband Message

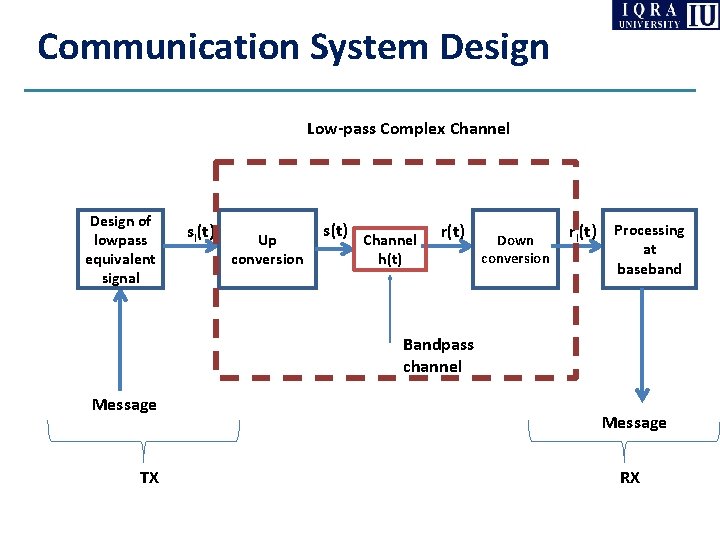
Communication System Design Low-pass Complex Channel Design of lowpass equivalent signal sl(t) Up conversion s(t) Channel r(t) h(t) Down conversion rl(t) Processing at baseband Bandpass channel Message TX Message RX

Envelope of bandpass signal This has shown another representation of bandpass signals in terms of envelope and phase with carrier frequency fc.

Effect of Conversion on Signal Energy Considering small intervals of envelope where the variations in amplitude are not significant and then integrating over those intervals will result in almost zero. Not exactly zero because the envelope will not be strictly constant. Hence energy of bandpasss signal is equal to almost half of lowpass signal energy

Response of Bandpass Channel in terms of Lowpass Channel response Suppose the response of bandpass system is h(t) so, h(t) H(f) And we know that h(t) is real ; implies that H(f)=H*(-f) conjugate symmetry |H(f)| h(t) is bandpass |H+(f)| |Hl(f)|

Response of Bandpass Channel in terms of Lowpass Channel response