Digital and NonLinear Control Digital Control System Time

Digital and Non-Linear Control Digital Control System Time Domain and Stability Analysis 1

Introduction • The time response of a discrete-time linear system is the solution of the difference equation governing the system. • For the linear time-invariant (LTI) case, the response due to the initial conditions and the response due to the input can be obtained separately and then added to obtain the overall response of the system. • Convert the system into z-domain. Compute the transfer function, and multiply it with the z-transform of the input signal. Convert the output signal to the time domain. 2

Example 1 • Given the discrete-time system • Find the impulse response of the system. Solution • Taking z-transform 3

Example 1 • Since U(z)=1 • Taking Inverse z-Transform 4

Example 2 • Given the discrete time system • find the system transfer function and its response to a sampled unit step. Solution • The transfer function corresponding to the difference equation is 5

Example 2 • 6

Final Value Theorem • If a sequence approaches a constant limit as k tends to infinity, then the limit is given by 7

Example 3 • Compute the final value for the sequence whose ztransform is Solution • Using final value theorem 8

Example 4 • Compute the final value for the sequence whose ztransform is Solution • Using final value theorem 9

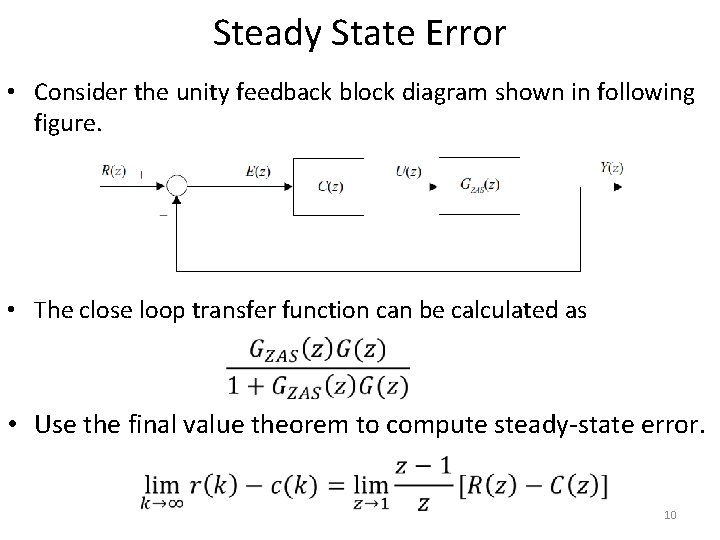
Steady State Error • Consider the unity feedback block diagram shown in following figure. • The close loop transfer function can be calculated as • Use the final value theorem to compute steady-state error. 10

Example 5 • 11

Example 5 • 12

Routh-Hurwitz Criterion • Determine the stability of linear time-invariant (LTI) digital systems based on transfer function models. The Routh-Hurwitz criterion determines conditions for left half plane (LHP) polynomial roots and cannot be directly used to investigate the stability of discrete-time systems. • The bilinear transformation transforms the inside of the unit circle to the LHP. This allows the use of the Routh-Hurwitz criterion for the investigation of discrete-time system stability. 13

Routh-Hurwitz Criterion • 14

Example 6 • Solution 15

Example 6 • Routh array can now be developed from the transformed characteristic equation. 0. 75 2. 5 0. 75 0 • Since there are no sign changes in the first column of the Routh array therefore the system is stable. 16

Example 7 • Solution 17

Example 7 • Routh array can now be developed from the transformed characteristic equation. -1. 875 4. 875 3. 875 1. 125 5. 419 0 1125 • From the table above, since there is one sign change in the first column above equation has one root in the right-half of the w-plane. • This implies that there will be one root of the characteristic equation outside of the unit circle in the z-plane. 18

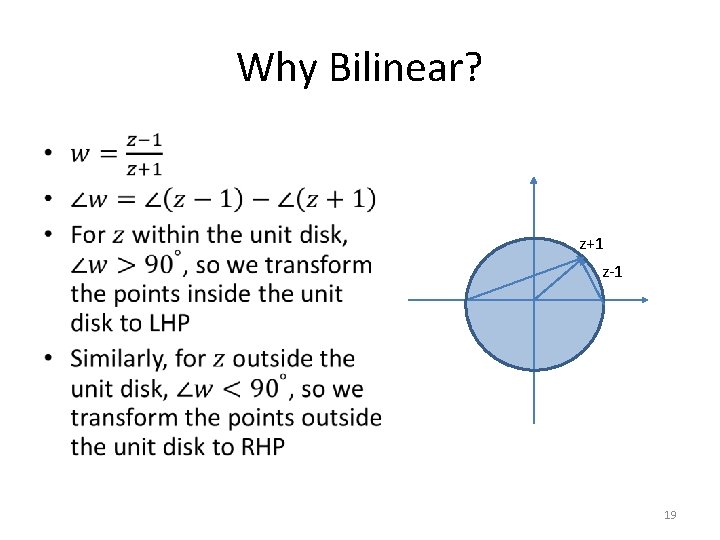
Why Bilinear? • z+1 z-1 19