Digestion in the small intestine Chris Budd Andre

Digestion in the small intestine Chris Budd, Andre Leger, Alastair Spence EPSRC CASE Award with Unilever

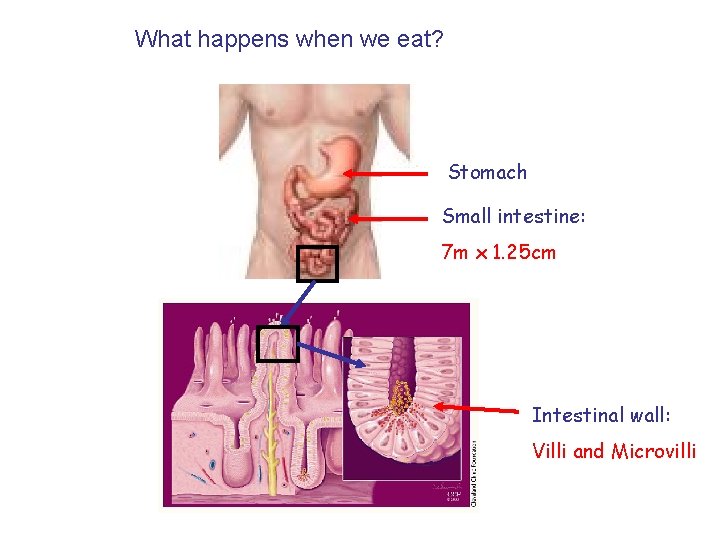
What happens when we eat? Stomach Small intestine: 7 m x 1. 25 cm Intestinal wall: Villi and Microvilli

Process: • Food enters stomach and leaves as Chyme • Nutrients are absorbed through the intestinal wall • Chyme passes through small intestine in 4. 5 hrs Intestinal wall Stomach Colon, illeocecal sphincter Peristaltic wave Mixing process

Objectives • Model the process of food moving through the intestine • Model the process of nutrient mixing and absorption Conclusions … • Peristalsis is effective at mixing the nutrients • It also acts to retard the mean flow of nutrient, allowing for greater nutrient absorption in the first part of the gut

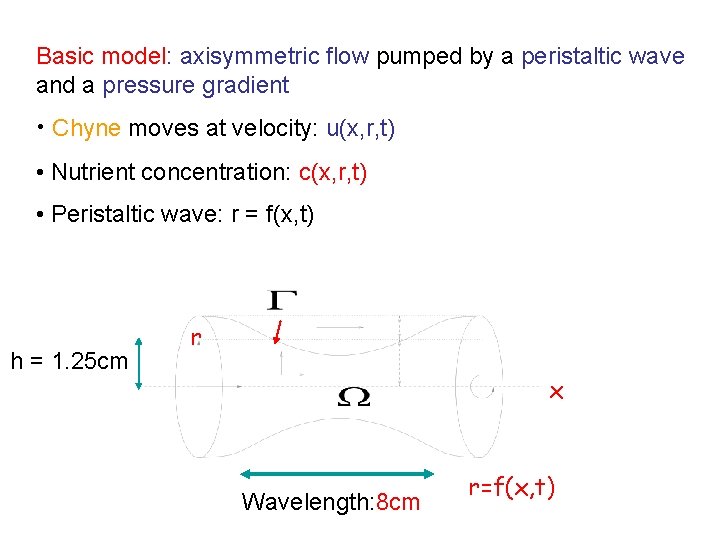
Basic model: axisymmetric flow pumped by a peristaltic wave and a pressure gradient • Chyne moves at velocity: u(x, r, t) • Nutrient concentration: c(x, r, t) • Peristaltic wave: r = f(x, t) h = 1. 25 cm r x Wavelength: 8 cm r=f(x, t)

Decouple the system: 1. Calculate the flow u of the Chyme assuming Stokes flow and long wavelength 2. Calculate the Nutrient transport and absorption

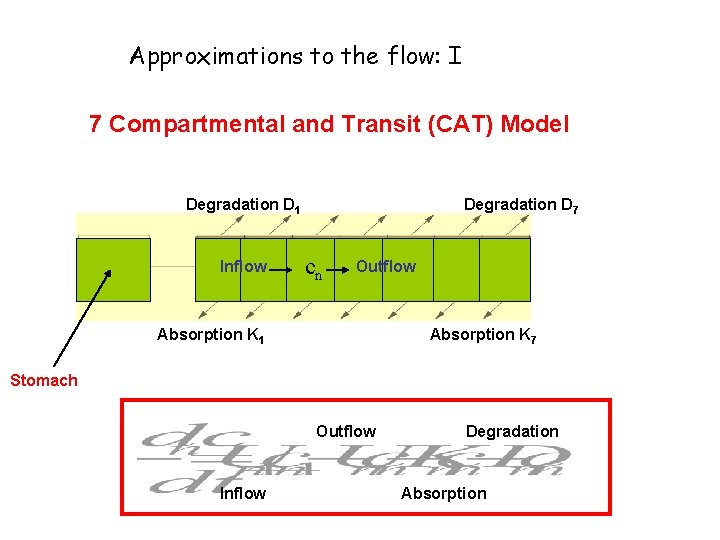
Approximations to the flow: I 7 Compartmental and Transit (CAT) Model Degradation D 1 Inflow Degradation D 7 cn Outflow INTESTINE Absorption K 1 Absorption K 7 Stomach Outflow Inflow Degradation Absorption

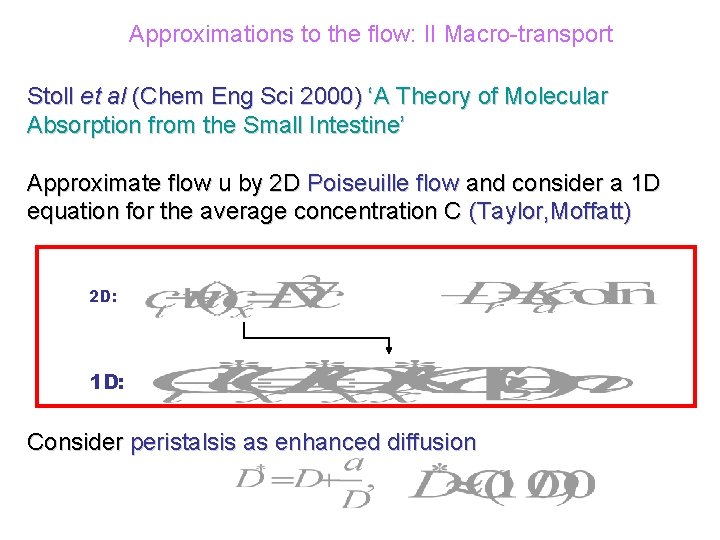
Approximations to the flow: II Macro-transport Stoll et al (Chem Eng Sci 2000) ‘A Theory of Molecular Absorption from the Small Intestine’ Approximate flow u by 2 D Poiseuille flow and consider a 1 D equation for the average concentration C (Taylor, Moffatt) 2 D: 1 D: Consider peristalsis as enhanced diffusion

Good news: Models are easy to use Bad news: results are poor fits to the numerically computed concentration profiles for complex peristaltic flow Better approach: 1. Use an asymptotic approach to give a good approximation to the peristaltic flow velocity u in the case of a small wave number 2. Identify different flow regimes 3. Use this in a numerical calculation of the concentration c

• Navier Stokes • Slow viscous Axisymmetric flow • Velocity & Stokes Streamfunction

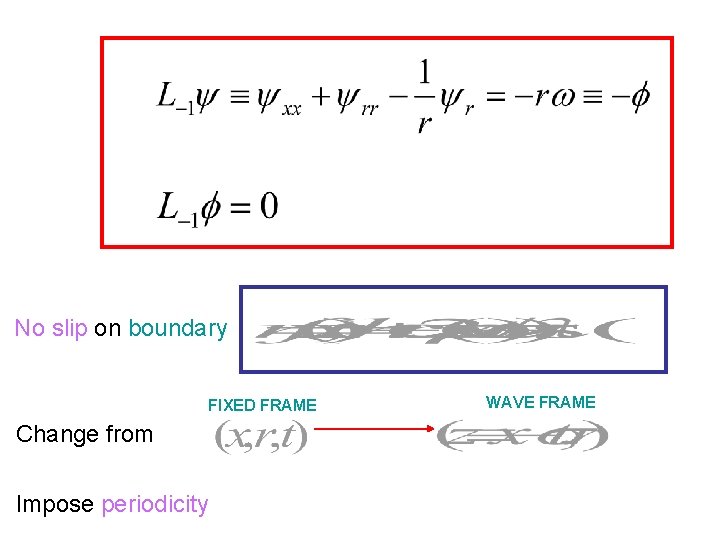
No slip on boundary FIXED FRAME Change from Impose periodicity WAVE FRAME

• Amplitude: Small parameters • Wave Number: Axisymmetry

Flow depends on: Flow rate Proportional to pressure drop Amplitude Wave number Develop asymptotic series in powers of gives Poiseuille flow

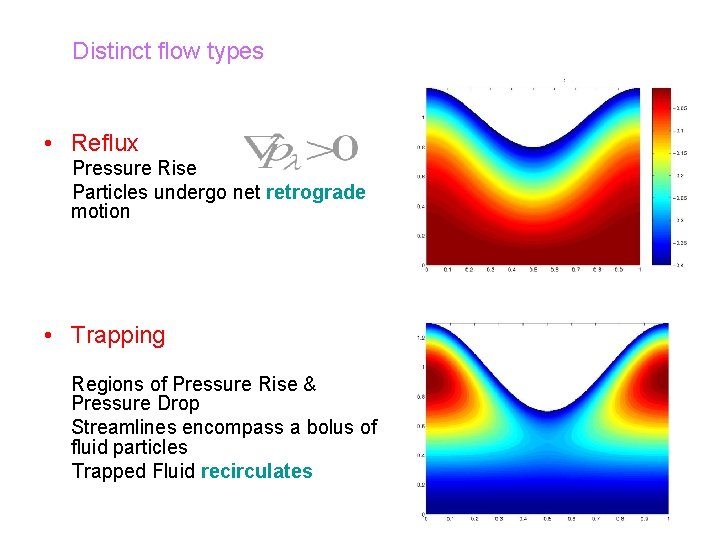
Distinct flow types • Reflux Pressure Rise Particles undergo net retrograde motion • Trapping Regions of Pressure Rise & Pressure Drop Streamlines encompass a bolus of fluid particles Trapped Fluid recirculates

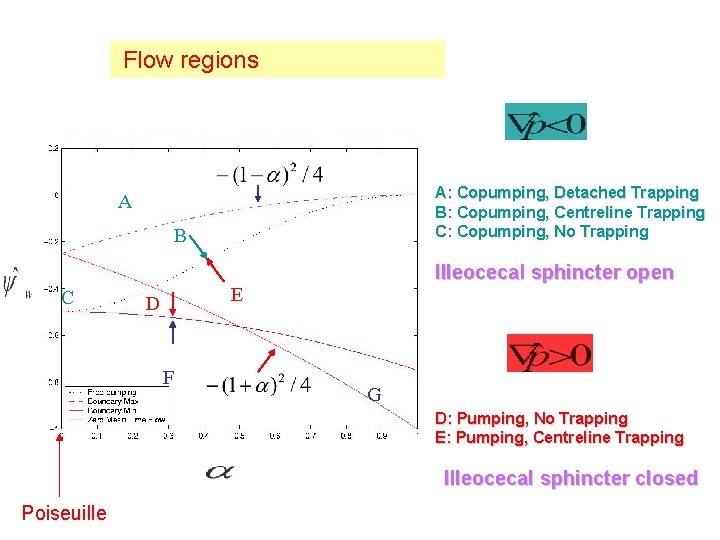
Flow regions A: Copumping, Detached Trapping B: Copumping, Centreline Trapping C: Copumping, No Trapping A B C Illeocecal sphincter open E D F G D: Pumping, No Trapping E: Pumping, Centreline Trapping Illeocecal sphincter closed Poiseuille

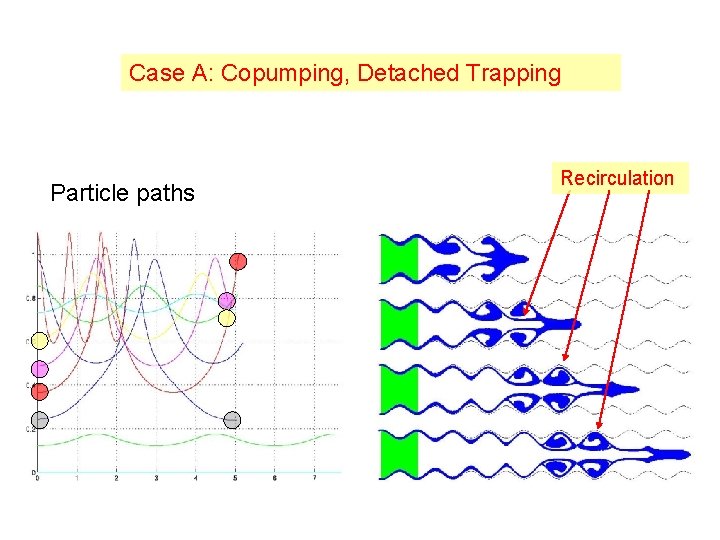
Case A: Copumping, Detached Trapping Particle paths Recirculation

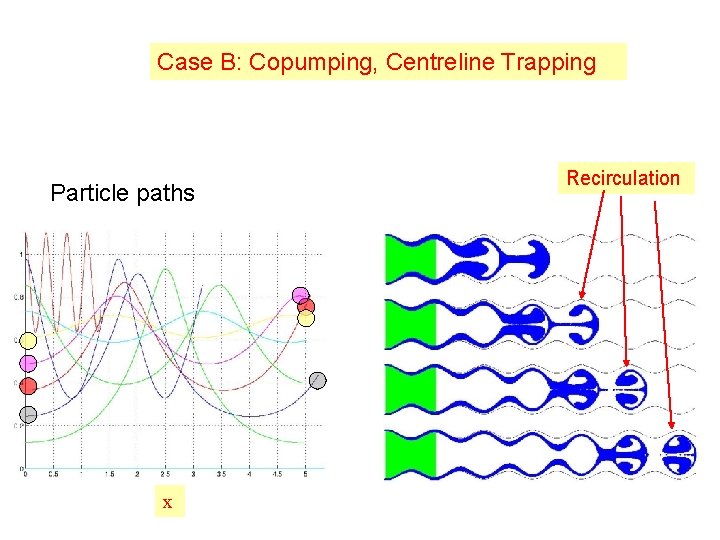
Case B: Copumping, Centreline Trapping Particle paths x Recirculation

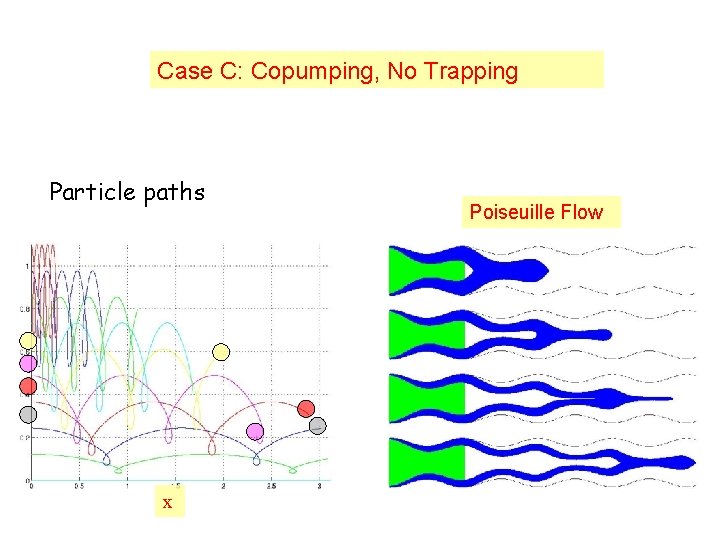
Case C: Copumping, No Trapping Particle paths x Poiseuille Flow

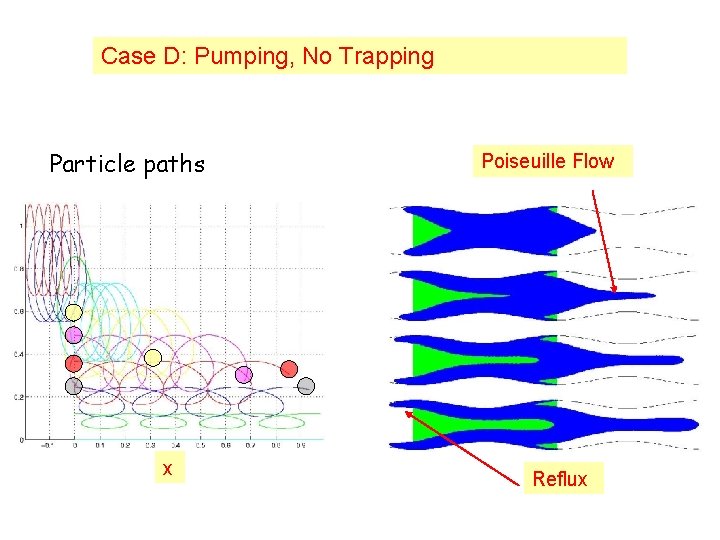
Case D: Pumping, No Trapping Particle paths x Poiseuille Flow Reflux

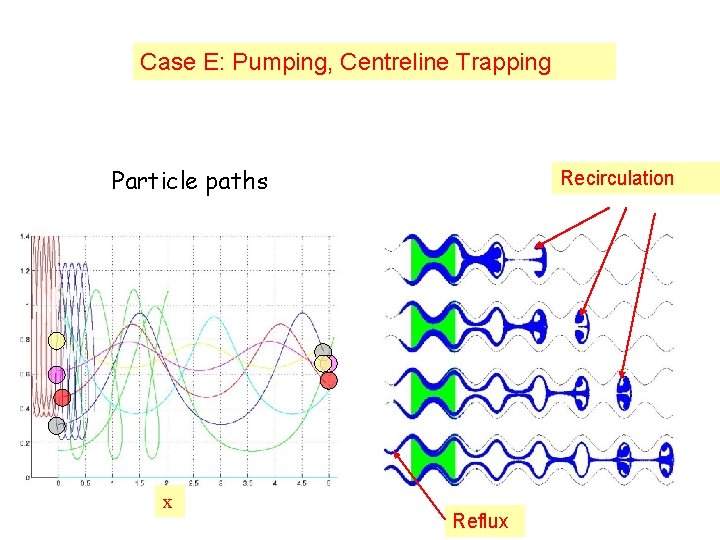
Case E: Pumping, Centreline Trapping Particle paths x Recirculation Reflux

Calculate the concentration c(x, r, t) 1. Substitute asymptotic solution for u into 2. Solve for c(x, r, t) numerically using an upwind scheme on a domain transformed into a computational rectangle. 3. Calculate rate of absorption

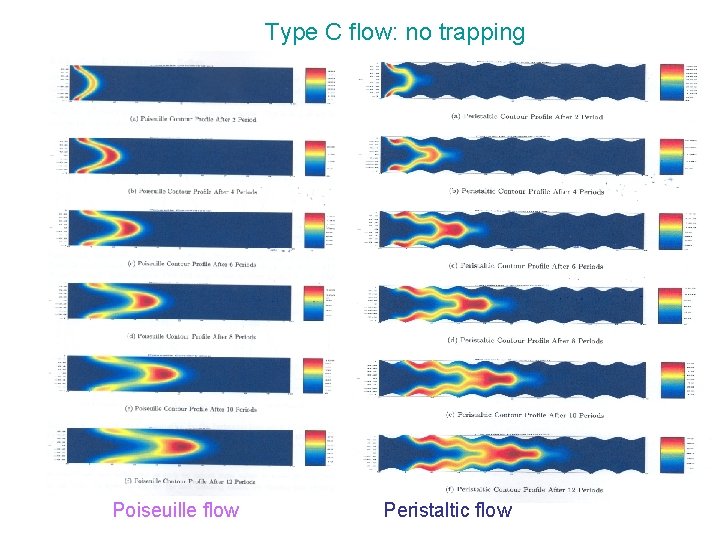
Type C flow: no trapping Poiseuille flow Peristaltic flow

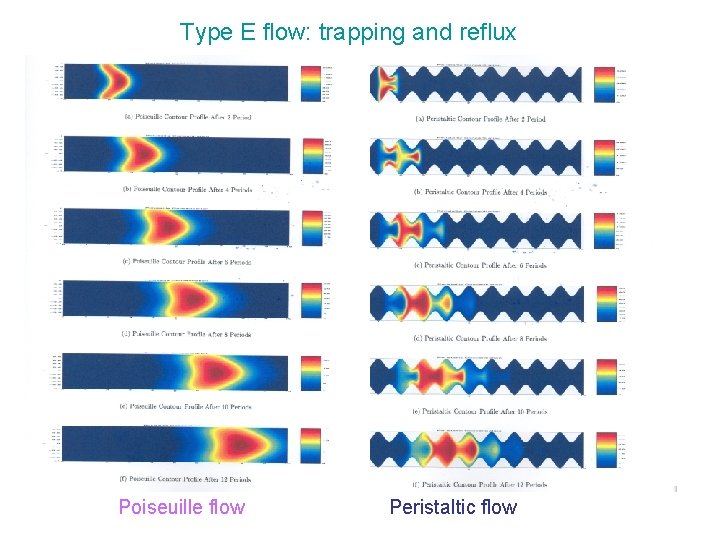
Type E flow: trapping and reflux Poiseuille flow Peristaltic flow

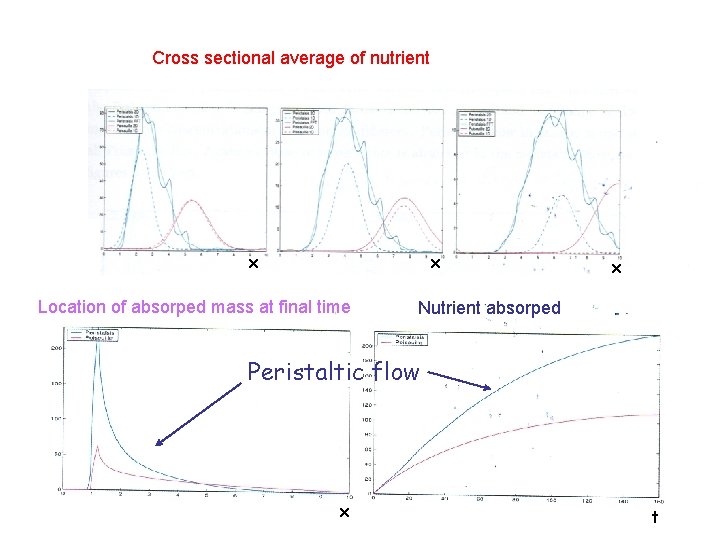
Cross sectional average of nutrient x x Location of absorped mass at final time x Nutrient absorped Peristaltic flow x t

Conclusions • Peristalsis helps both pumping and mixing • Significantly greater absorption with Peristaltic flow than with Poiseuille flow Next steps • Improve the absorption model • Improve the fluid model (Non-Newtonian flow) • More accurate representation of the intestine geometry • Experiments