Diffusion Tensor Processing and Visualization Ross Whitaker University

Diffusion Tensor Processing and Visualization Ross Whitaker University of Utah National Alliance for Medical Image Computing

Acknowledgments Contributors: • A. Alexander • G. Kindlmann • L. O’Donnell • J. Fallon National Alliance for Medical Image Computing (NIH U 54 EB 005149)

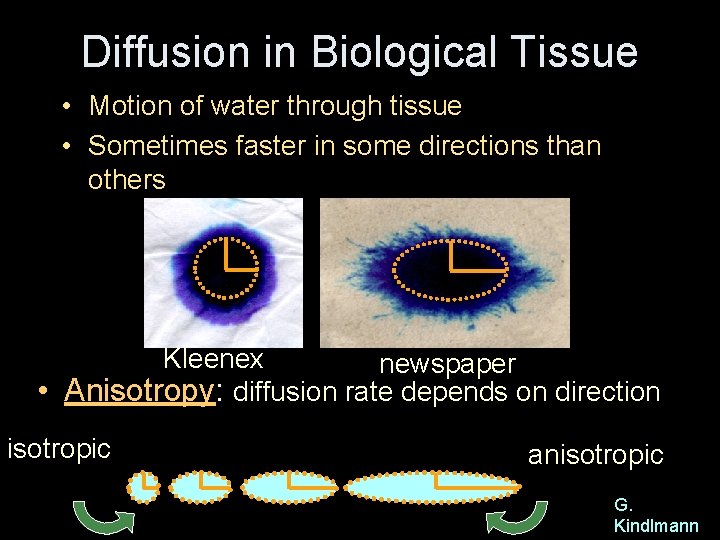
Diffusion in Biological Tissue • Motion of water through tissue • Sometimes faster in some directions than others Kleenex newspaper • Anisotropy: diffusion rate depends on direction isotropic anisotropic G. Kindlmann

The Physics of Diffusion • Density of substance changes (evolves) over time according to a differential equation (PDE) Change Derivatives in (gradients) in density Diffusion – space matrix, tensor (2 x 2 or 3 x 3)

Solutions of the Diffusion Equation • Simple assumptions – Small dot of a substance (point) – D constant everywhere in space • Solution is a multivariate Gaussian – Normal distribution – D plays the role of the covariance matrix • This relationship is not a coincidence – Probabilistic models of diffusion (random walk)

D Is A Special Kind of Matrix • The universe of matrices Matrices Square Skew symmetric Nonsquare D is a “square, symmetric, positivedefinite matrix” Symmetric (SPD) Positive

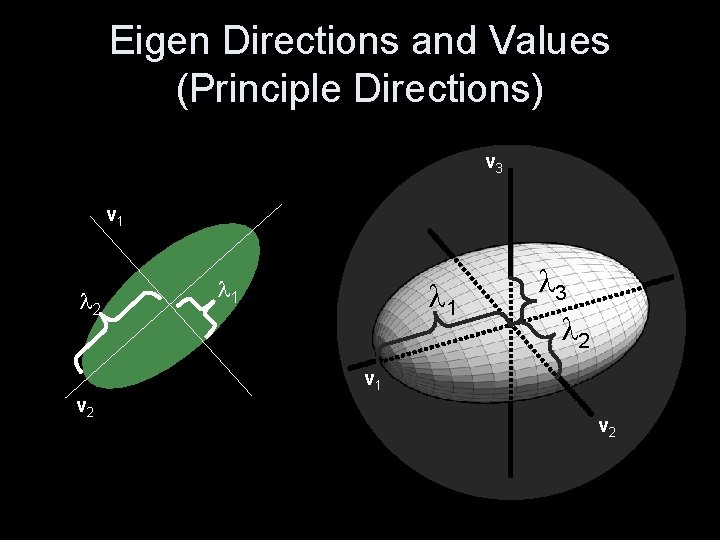
Properties of SPD • Bilinear forms and quadratics Quadratic equation – implicit equation for ellipse (ellipsoid in 3 D) • Eigen Decomposition – Lambda – shape information, independent of orientation – R – orientation, independent of shape – Lambda’s > 0

Eigen Directions and Values (Principle Directions) v 3 v 1 2 1 1 3 2 v 1 v 2

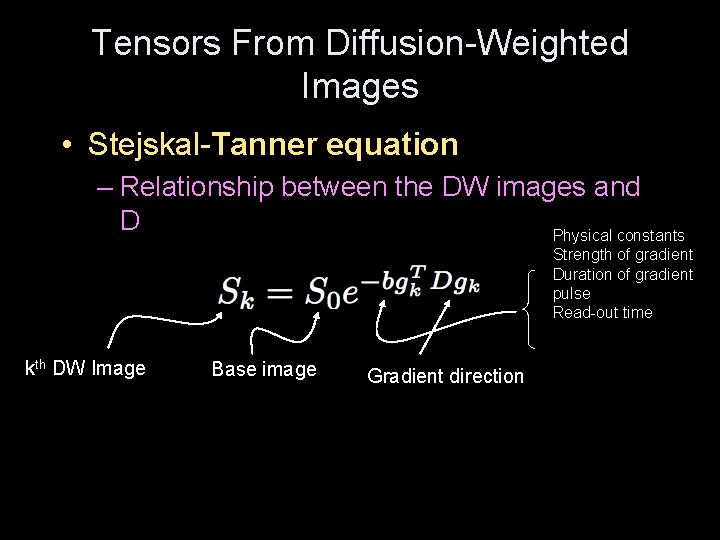
Tensors From Diffusion-Weighted Images • Big assumption – At the scale of DW-MRI measurements – Diffusion of water in tissue is approximated by Gaussian • Solution to heat equation with constant diffusion tensor • Stejskal-Tanner equation – Relationship between the DW images and Physical constants Strength of gradient D kth DW Image Base image Gradient direction Duration of gradient pulse Read-out time

Tensors From Diffusion-Weighted Images • Stejskal-Tanner equation – Relationship between the DW images and D Physical constants Strength of gradient Duration of gradient pulse Read-out time kth DW Image Base image Gradient direction

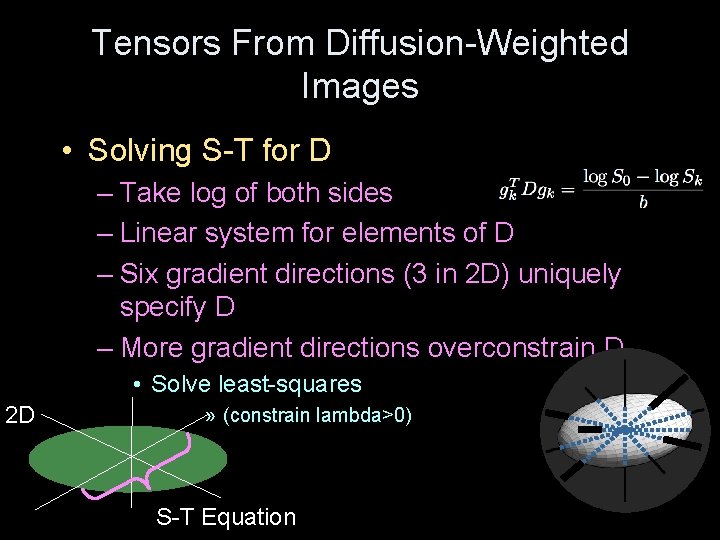
Tensors From Diffusion-Weighted Images • Solving S-T for D – Take log of both sides – Linear system for elements of D – Six gradient directions (3 in 2 D) uniquely specify D – More gradient directions overconstrain D • Solve least-squares 2 D » (constrain lambda>0) S-T Equation

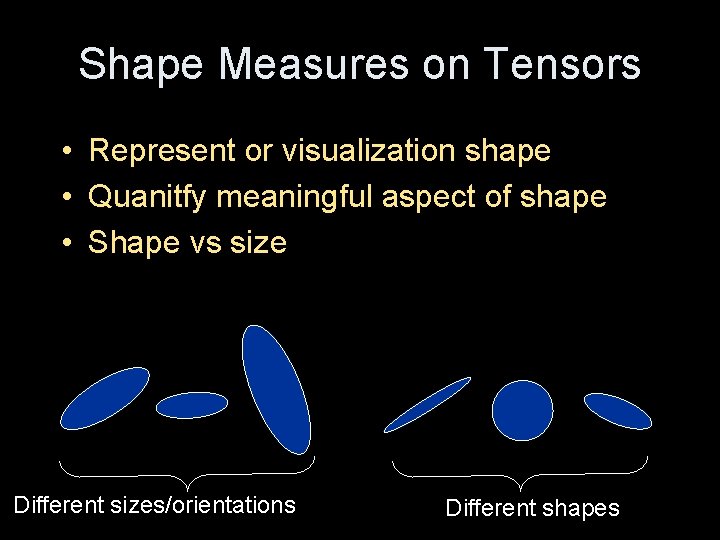
Shape Measures on Tensors • Represent or visualization shape • Quanitfy meaningful aspect of shape • Shape vs size Different sizes/orientations Different shapes

Measuring the Size of A Tensor • Length – ( 1 + 2 + 3)/3 – ( 12 + 22 + 32)1/2 • Area – ( 1 2 + 1 3 + 2 3) • Volume – ( 1 2 3) Sometimes used. Generally used. Also called: “Root sum of squares” “Mean diffusivity” “Diffusion norm” “Trace” “Frobenius norm”

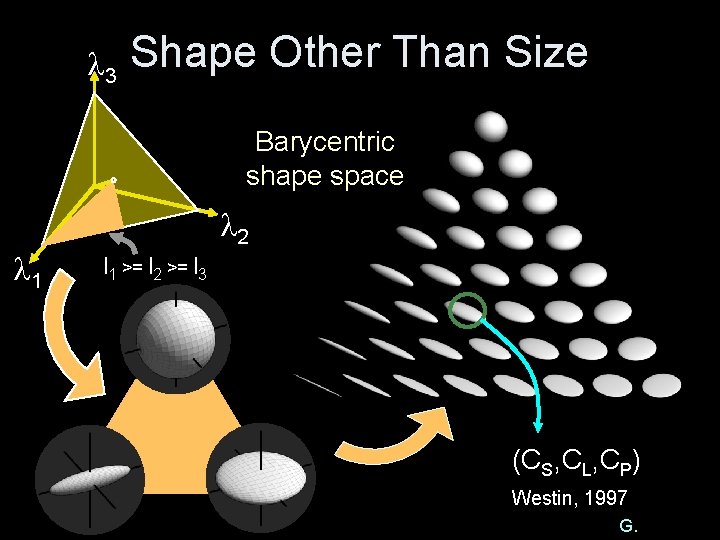
3 Shape Other Than Size Barycentric shape space 1 2 l 1 >= l 2 >= l 3 (CS, CL, CP) Westin, 1997 G.

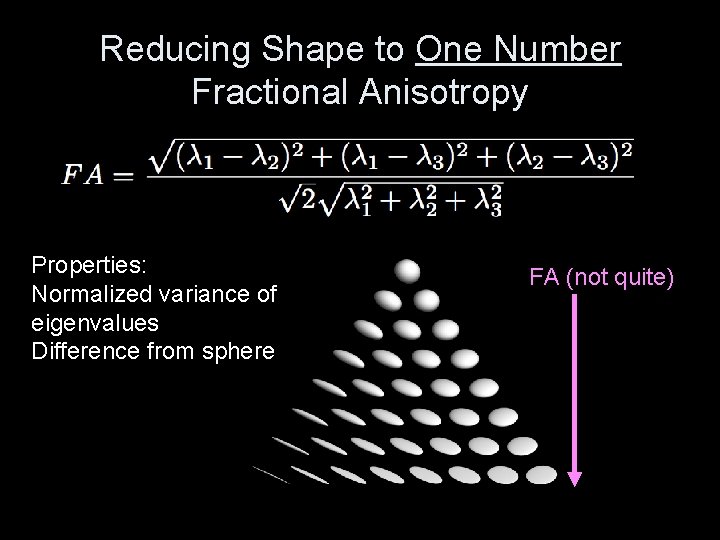
Reducing Shape to One Number Fractional Anisotropy Properties: Normalized variance of eigenvalues Difference from sphere FA (not quite)

FA As An Indicator for White Matter • Visualization – ignore tissue that is not WM • Registration – Align WM bundles • Tractography – terminate tracts as they exit WM • Analysis – Axon density/degeneration – Myelin • Big question – What physiological/anatomical property does FA measure?

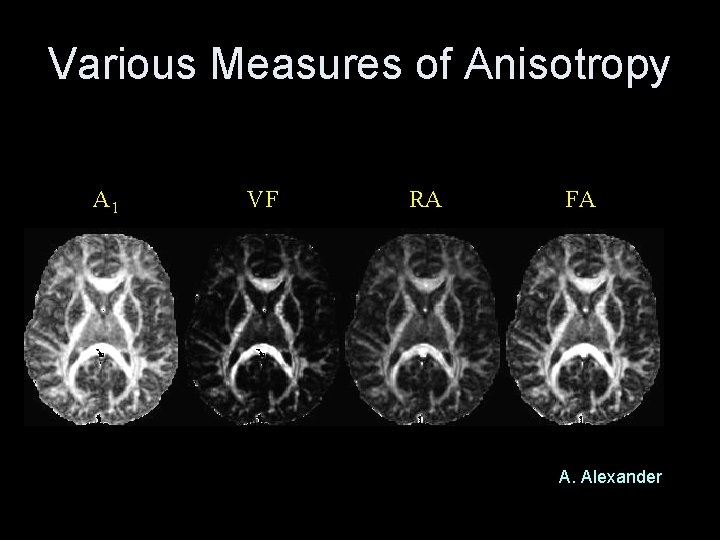
Various Measures of Anisotropy A 1 VF RA FA A. Alexander

Visualizing Tensors: Direction and Shape • Color mapping • Glyphs

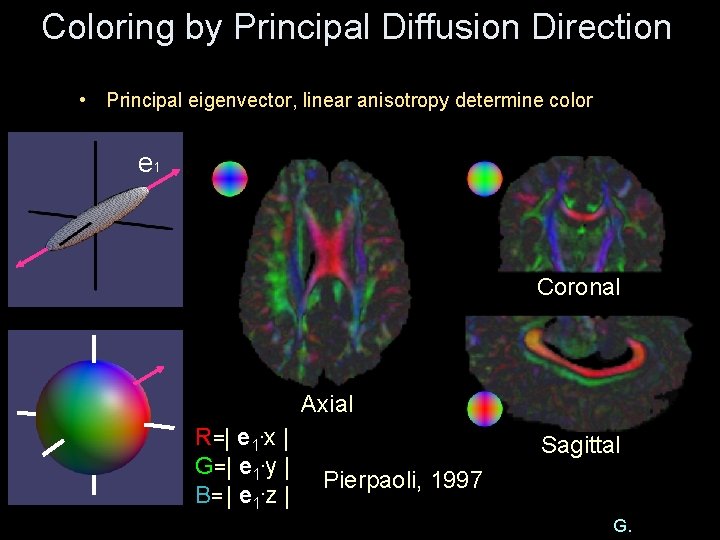
Coloring by Principal Diffusion Direction • Principal eigenvector, linear anisotropy determine color e 1 Coronal Axial R = | e 1. x | G = | e 1. y | B = | e 1. z | Sagittal Pierpaoli, 1997 G.

Issues With Coloring by Direction • Set transparency according to FA (highlighttracts) • Coordinate system dependent • Primary colors dominate – Perception: saturated colors tend to look more intense – Which direction is “cyan”?

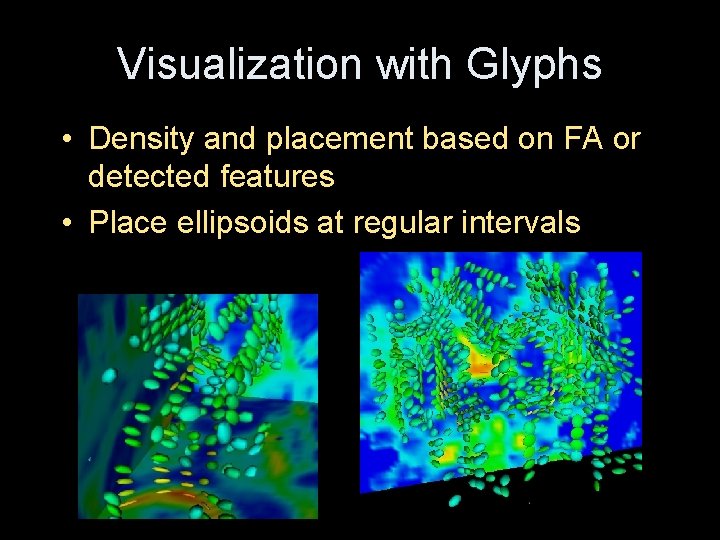
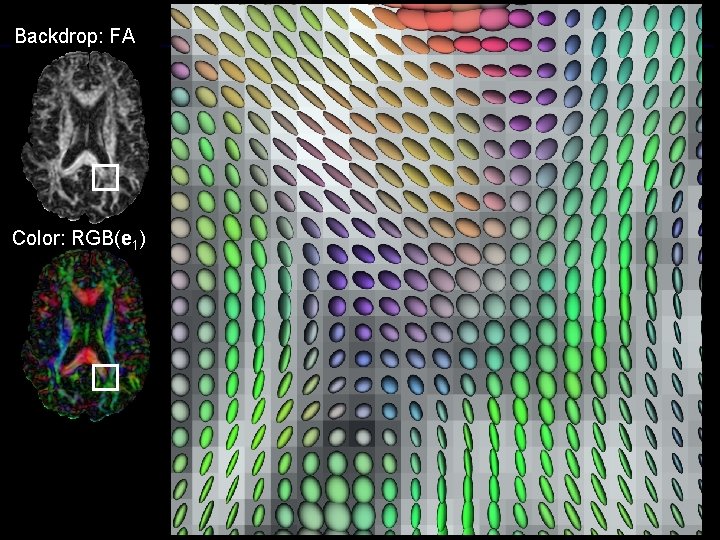
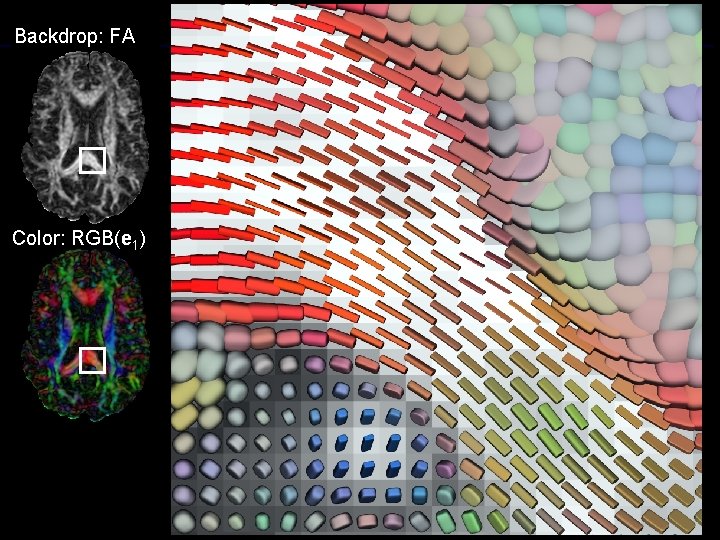
Visualization with Glyphs • Density and placement based on FA or detected features • Place ellipsoids at regular intervals

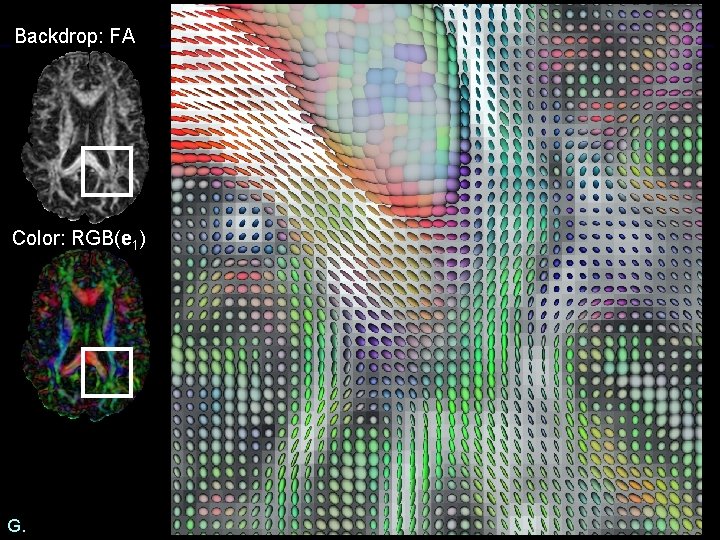
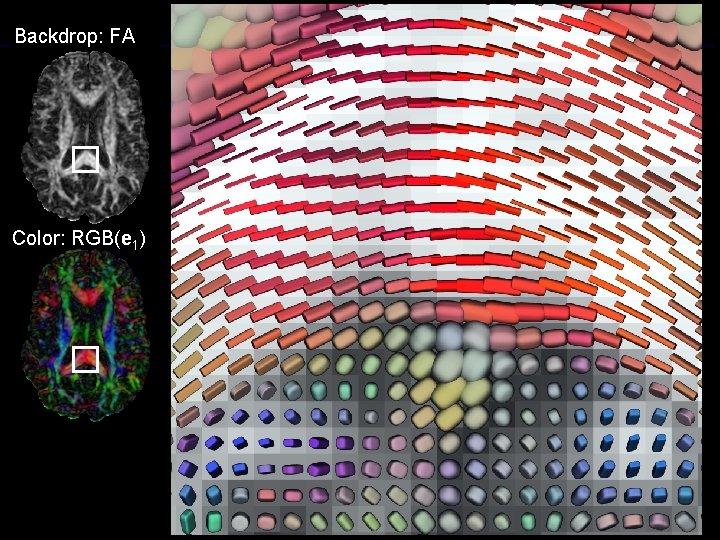
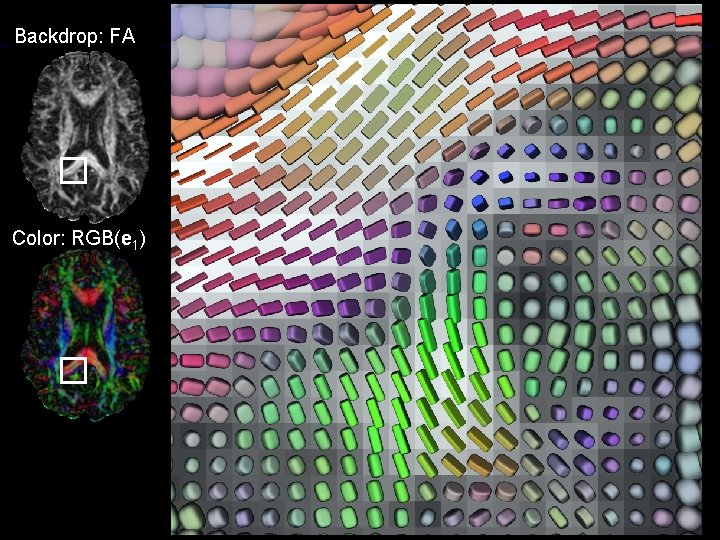
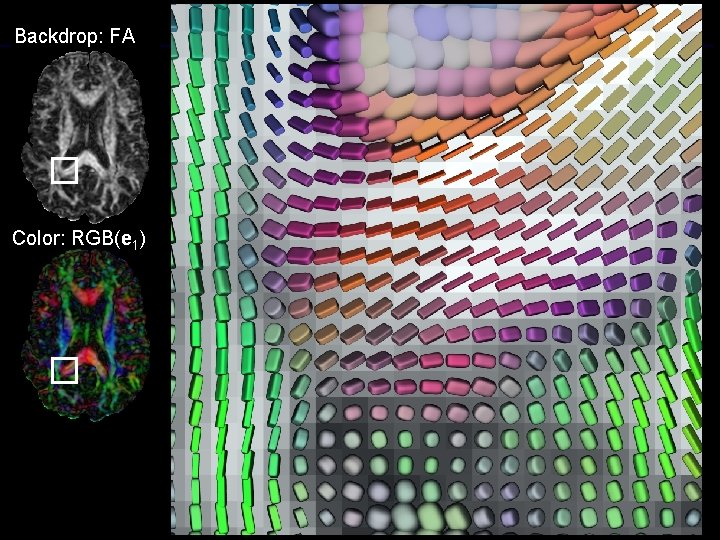
Backdrop: FA Color: RGB(e 1) G.

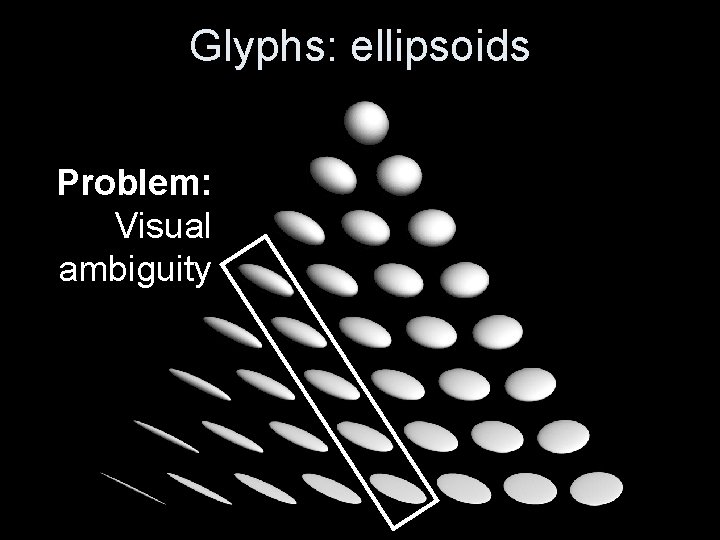
Glyphs: ellipsoids Problem: Visual ambiguity

Worst case scenario: ellipsoids one viewpoint: another viewpoint:

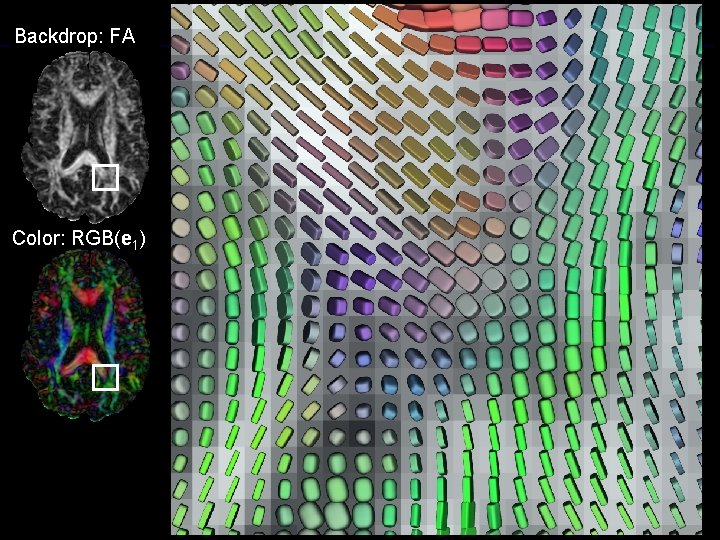
Glyphs: cuboids Problem: missing symmetry

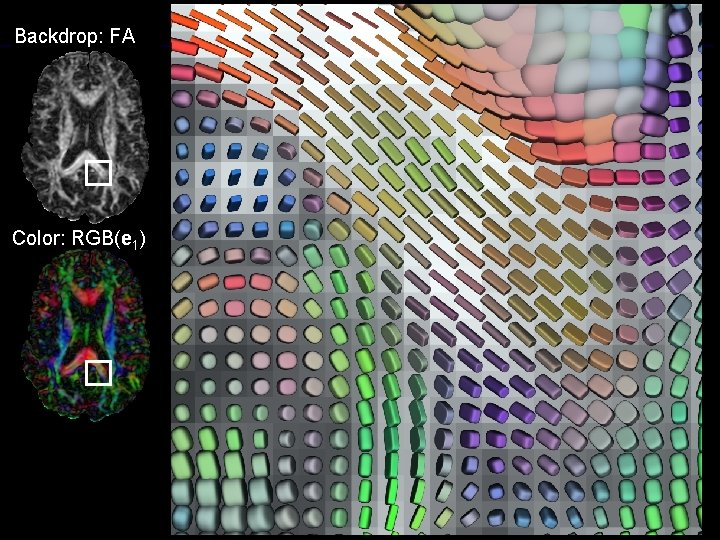
Superquadrics Barr 1981

Superquadric Glyphs for Visualizing DTI Kindlmann 2004

Worst case scenario, revisited

Backdrop: FA Color: RGB(e 1)

Backdrop: FA Color: RGB(e 1)

Backdrop: FA Color: RGB(e 1)

Backdrop: FA Color: RGB(e 1)

Backdrop: FA Color: RGB(e 1)

Backdrop: FA Color: RGB(e 1)

Backdrop: FA Color: RGB(e 1)

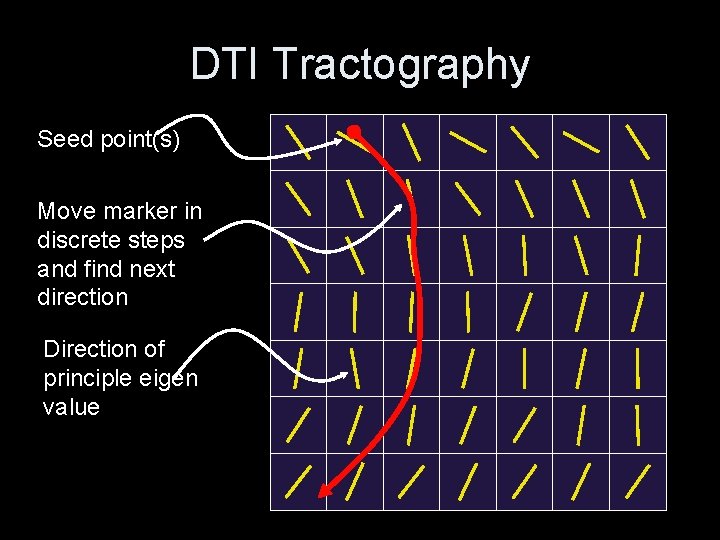
Going Beyond Voxels: Tractography • Method for visualization/analysis • Integrate vector field associated with grid of principle directions • Requires – Seed point(s) – Stopping criteria • FA too low • Directions not aligned (curvature too high) • Leave region of interest/volume

DTI Tractography Seed point(s) Move marker in discrete steps and find next direction Direction of principle eigen value

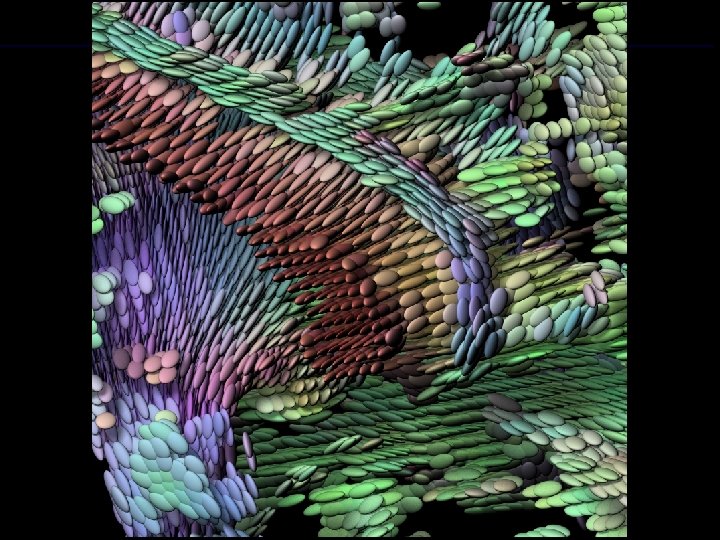
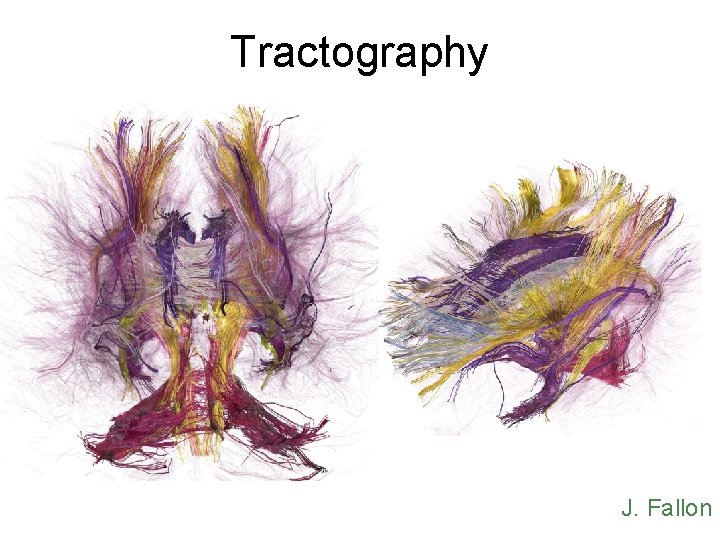
Tractography J. Fallon

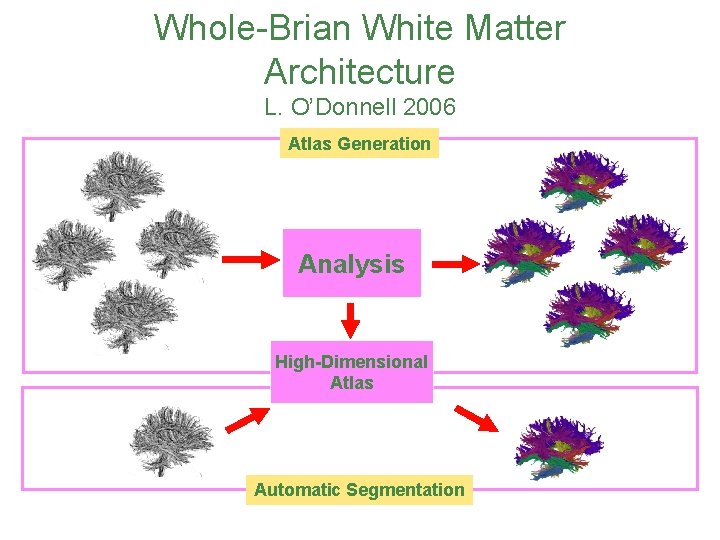
Whole-Brian White Matter Architecture L. O’Donnell 2006 Atlas Generation Analysis High-Dimensional Saved structure information Atlas Automatic Segmentation

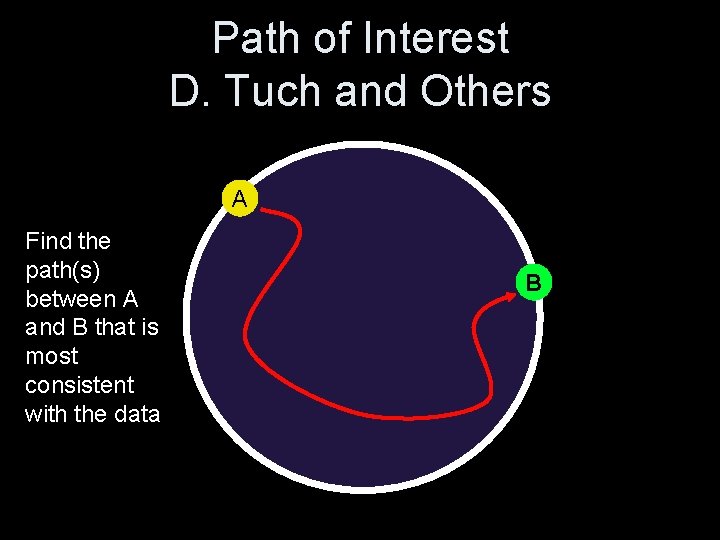
Path of Interest D. Tuch and Others A Find the path(s) between A and B that is most consistent with the data B

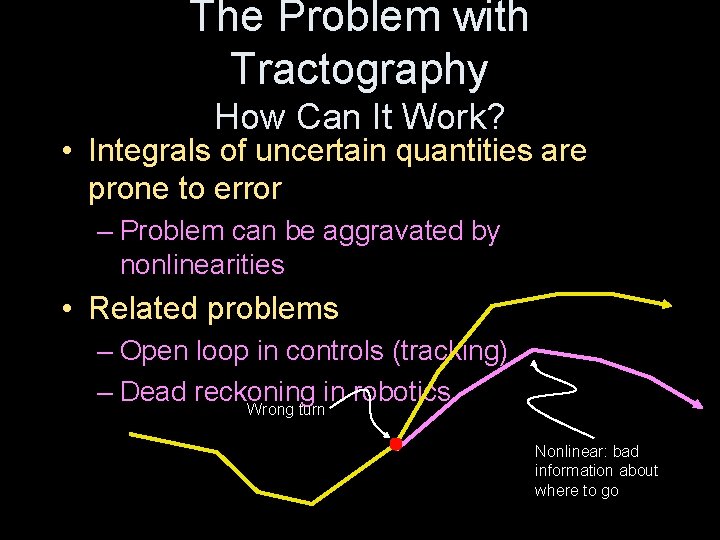
The Problem with Tractography How Can It Work? • Integrals of uncertain quantities are prone to error – Problem can be aggravated by nonlinearities • Related problems – Open loop in controls (tracking) – Dead reckoning in robotics Wrong turn Nonlinear: bad information about where to go

Mathematics and Tensors • Certain basic operations we need to do on tensors – – – Interpolation Filtering Differences Averaging Statistics • Danger – Tensor operations done element by element • Mathematically unsound • Nonintuitive

Averaging Tensors • What should be the average of these two tensors? Linear Average Componentwise

Arithmetic Operations On Tensor • Don’t preserve size – Length, area, volume • Reduce anisotropy • Extrapolation –> nonpositive, nonsymmetric • Why do we care? – Registration/normalization of tensor images – Smoothing/denoising – Statistics mean/variance

What Can We Do? (Open Problem) • Arithmetic directly on the DW images – How to do statics? – Rotational invariance • Operate on logarithms of tensors (Arsigny) – Exponent always positive • Riemannian geometry (Fletcher, Pennec) – Tensors live in a curved space

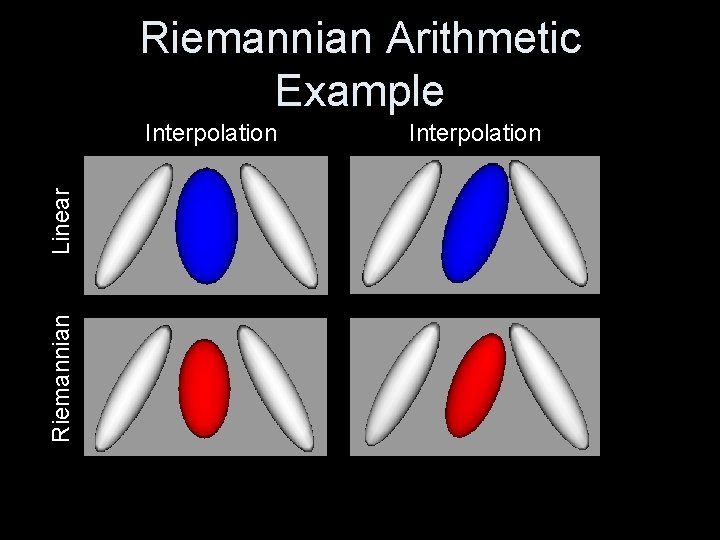
Riemannian Arithmetic Example Riemannian Linear Interpolation

Low-Level Processing DTI Status • Set of tools in ITK – Linear and nonlinear filtering with Riemannian geometry – Interpolation with Riemannian geometry – Set of tools for processing/interpolation of tensors from DW images • More to come…

Questions