Diffusion of ions and electrons in gas Lecture

Diffusion of ions and electrons in gas Lecture 5

Thermal movement and Diffusion of ions and electrons in gas (Leo) Ions and electrons released by ionization undergo multiple collisions: == > thermal equilibrium Maxwell Boltzmann: == > ve >> vion ! At room temperature: vion =100 m/s ve = 10 km/s Diffusion: Spread of initially localized particles as a consequence of thermal motion, kinetic theory: Gaussian distribution after time t in one dimension: N 0: total number of charges x: distance from point of creation D: Diffusion coefficient (ex. O 2 : D=0. 06 cm 2/s, x=6 mm after 1 s) Rms in 1 -dim: In 3 -dim: Kinetic theory: Classical ideal gas: For ideal gas: λ: mean free path σ0: total cross section for collision with gas molecule p: pressure (Kleinknecht)

Drift and mobility Electrons and ions in electric field: Acceleration from field, but deceleration via collisions, after some time, a constant drift velocity v. D (superimposed on random thermal movement) is reached. μ: mobility of ion or electron in gas For positive ions: p: pressure For electrons, longer mean free path, therefore more acceleration; inelastic collision. The electron drift velocity is increased with higher methan proportion – it is the methan that slows the electrons down – the electrons are then at an energy with lower cross section and its velocity is increasing. Beyond the maximum the inelastic cross section is increased and the drift velocity is decreasing Molecular: inelastic collisions Ar, atomic

For ideal gas, simple relation between drift and diffusion: Einstein relation Drift in magnetic field: no longer , angle between and : Lorentz or drift angle α, for E and B field orthogonal: : Cyclotron frequency : mean time between collisions

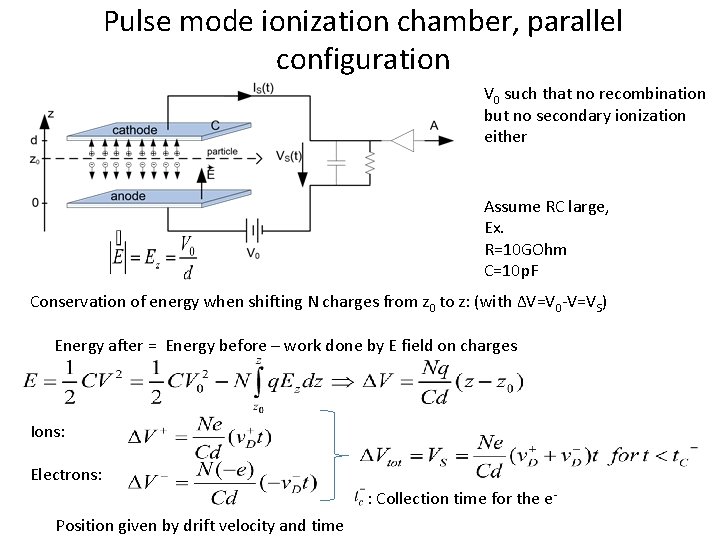
Pulse mode ionization chamber, parallel configuration V 0 such that no recombination but no secondary ionization either Assume RC large, Ex. R=10 GOhm C=10 p. F Conservation of energy when shifting N charges from z 0 to z: (with ΔV=V 0 -V=VS) Energy after = Energy before – work done by E field on charges Ions: Electrons: : Collection time for the e. Position given by drift velocity and time

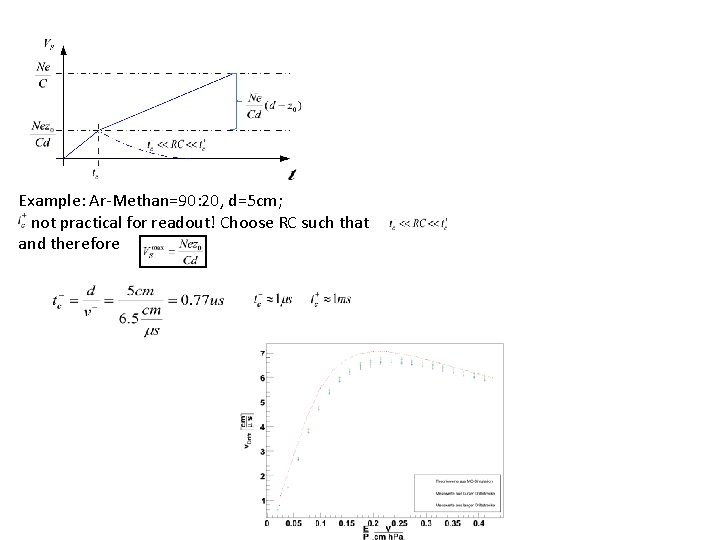
Example: Ar-Methan=90: 20, d=5 cm; not practical for readout! Choose RC such that and therefore

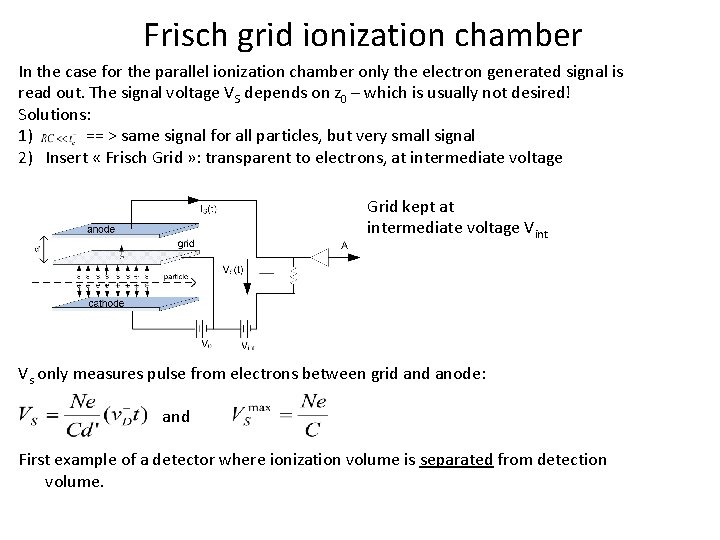
Frisch grid ionization chamber In the case for the parallel ionization chamber only the electron generated signal is read out. The signal voltage VS depends on z 0 – which is usually not desired! Solutions: 1) == > same signal for all particles, but very small signal 2) Insert « Frisch Grid » : transparent to electrons, at intermediate voltage Grid kept at intermediate voltage Vint Vs only measures pulse from electrons between grid anode: and First example of a detector where ionization volume is separated from detection volume.

Pulse mode ionization chamber, cylindrical configuration Electrons and ions are formed at r=r 0, energy conservation as for parallel configuration: For example ions: r 0 -> re: For electron pulse dominates, ex. ,

What is the collection time for electrons? assume , ( is a good assumption for E/p < 1 V/cmk. Pa) Ex. V 0=100 V, ,

Current mode ionization chamber (Röntgen unit) If cannot measure individual particles, measure average current. N: total number of charges released through ionization during time constant RC Used for measurement of exposure (γ-rays, α, β) Typically with air because radiation units are defined in air: 1 Röntgen= quantity of X-or γ-rays producing ionization of 1 esu/cm 3 (2. 58*10 -4 C/kg) in air at STP. More relevant units 1 Gy=1 J/kg for absorbed dose 1 Sv=1 J/kg for equivalent dose (weighted) Ex. α-source of 10 k. Bq (0. 27μCi), Eα=5 Me. V, gaz: dry air with wi=34 e. V, particles lose all energy in chamber:

Signal amplification via Townsend avalanches: PPAC and proportional chamber The main problem of the ionization chamber is its small signal ! Solution: increase the electric field in the gas volume! If the E-field is strong enough, the liberated electrons will gain sufficient kinetic energy to produce secondary ionization and therefore more electrons are liberated which in turn can further ionize. == > “Townsend” avalanche The collected charge is then amplified by a factor A which is called the “Gain” Again we may consider two basic geometries: 1) Parallel configuration: (E uniform) Parallel Plate Avalanche Chamber (PPAC) Clearly Q 1>Q 2: the amplification depends on the location of the ionization! The chamber is not proportional! Double-stage PPAC Separation of low-field ionization region from high-field amplification region with a grid (Frisch Grid) ==> uniform amplification Practical disadvantages are the high voltage needed and the mechanical stability – compared to cylindrical proportional chamber, therefore much less used. [“Revival” in the form of “micro pattern” detectors: GEM, Micromegas, Cat].

2) Cylindrical configuration “the” Proportional Chamber (PC) Thanks to field, inherent separation of gas volume into large ionization region and small amplification region! With thin wire (typically 20 -100μm) a high electric field is achieved with relatively low voltage (a few 100 V)