Diffusion in Gas DIFFUSION DEFINITIONS Diffusion is a

Diffusion in Gas

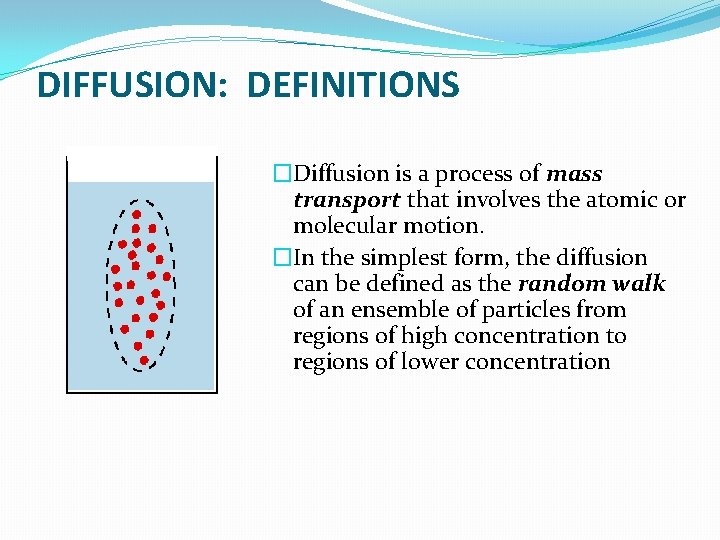
DIFFUSION: DEFINITIONS �Diffusion is a process of mass transport that involves the atomic or molecular motion. �In the simplest form, the diffusion can be defined as the random walk of an ensemble of particles from regions of high concentration to regions of lower concentration

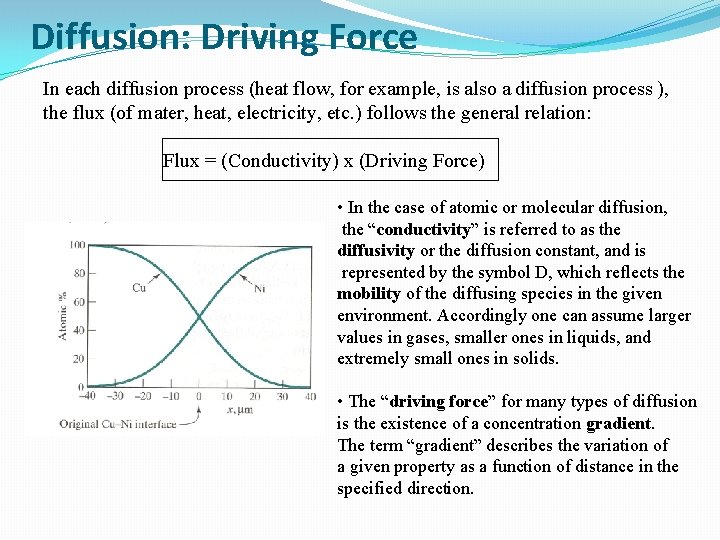
Diffusion: Driving Force In each diffusion process (heat flow, for example, is also a diffusion process ), the flux (of mater, heat, electricity, etc. ) follows the general relation: Flux = (Conductivity) x (Driving Force) • In the case of atomic or molecular diffusion, the “conductivity” is referred to as the diffusivity or the diffusion constant, and is represented by the symbol D, which reflects the mobility of the diffusing species in the given environment. Accordingly one can assume larger values in gases, smaller ones in liquids, and extremely small ones in solids. • The “driving force” for many types of diffusion is the existence of a concentration gradient. The term “gradient” describes the variation of a given property as a function of distance in the specified direction.

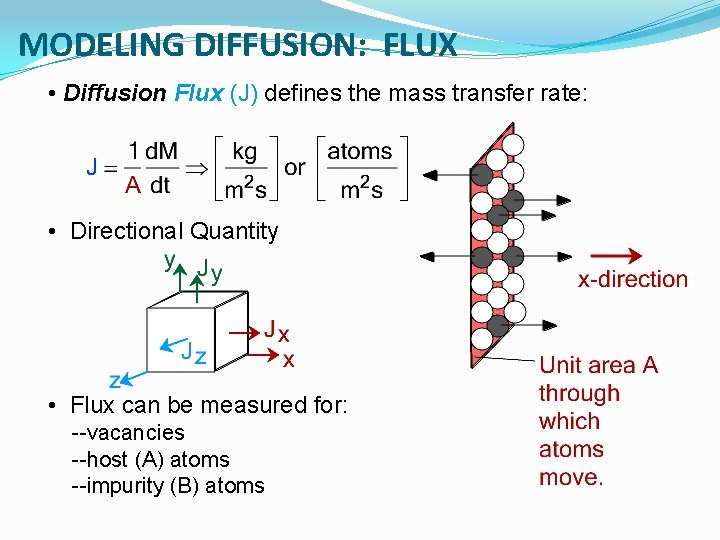
MODELING DIFFUSION: FLUX • Diffusion Flux (J) defines the mass transfer rate: • Directional Quantity • Flux can be measured for: --vacancies --host (A) atoms --impurity (B) atoms

STEADY-STATE DIFFUSION (Fick’s First Law) SSD takes place at constant rate. It means that throughout the system d. C/dx=const and d. C/dt=0 DC/ Dx d. C/dx DC Dx - Fick’s first law The diffusion flux is proportional to the existing concentration gradient

FIRST FICK’s LAW where D is the diffusion constant or diffusivity [m 2/s] and C is a concentration [kg/m 3] ey ez Jy Jz D=D 0 exp(-Qd/RT) Jx ex here Q is the activation energy for the process: [J/mol]; Do is temperature-independent pre-exponential constant: [m 2/s]

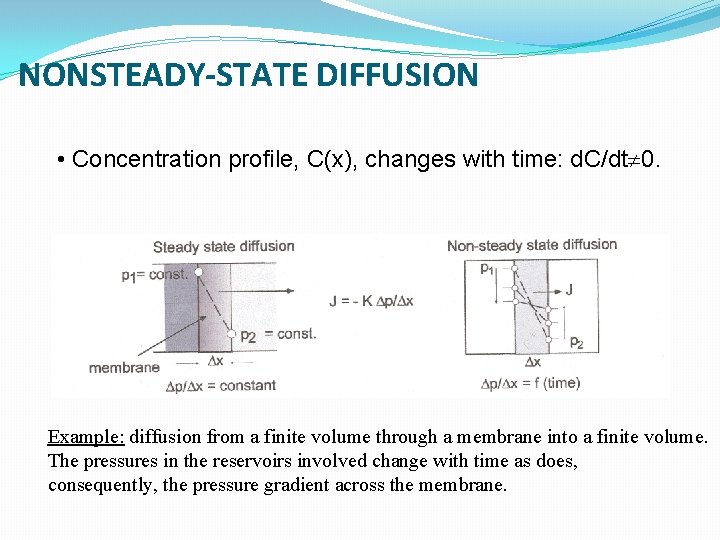
NONSTEADY-STATE DIFFUSION • Concentration profile, C(x), changes with time: d. C/dt 0. Example: diffusion from a finite volume through a membrane into a finite volume. The pressures in the reservoirs involved change with time as does, consequently, the pressure gradient across the membrane.

FICK’s SECOND LAW Consider a volume element (between x and x+dx of unit cross section) in a diffusion system. The flux of a given material into a volume element (Jx) minus the flux out of the element volume (Jx+dx) equals the rate of material accumulation in the volume: x Using a Taylor series we can expand Jx+dx: Accordingly, as dx 0 and using Fick’s First Law: And if D does not vary with x we have The formulation of Fick’s Second Law:

EX: NON STEADY STATE DIFFUSION • Copper diffuses into a semi-infinite bar of aluminum. Boundary conditions: For t=0, C=C 0 at 0 x For t>0, C=Cs at x=0 C=C 0 at x = • General solution: æ x ö C(x, t ) - Co = ÷ 1 erf çè 2 Dt ø Cs - Co

Error Function � The terms erf and erfc stand for error function and complementary error function respectively - it is the Gaussian error function as tabulated (like trigonometric and exponential functions) in mathematical tables. (see Table 5. 1, Callister 6 e). � Its limiting values are:

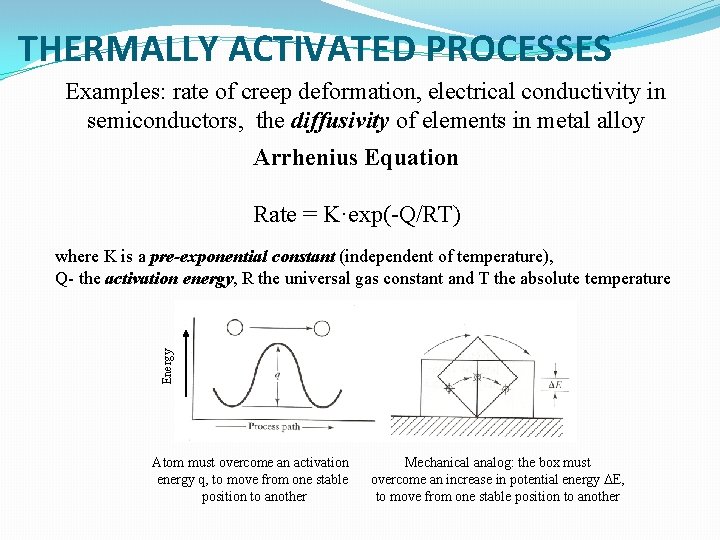
THERMALLY ACTIVATED PROCESSES Examples: rate of creep deformation, electrical conductivity in semiconductors, the diffusivity of elements in metal alloy Arrhenius Equation Rate = K·exp(-Q/RT) Energy where K is a pre-exponential constant (independent of temperature), Q- the activation energy, R the universal gas constant and T the absolute temperature Atom must overcome an activation energy q, to move from one stable position to another Mechanical analog: the box must overcome an increase in potential energy DE, to move from one stable position to another

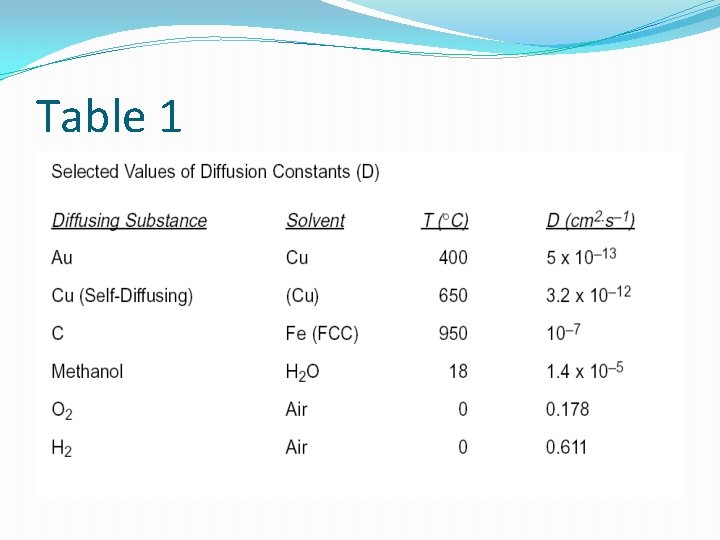
Table 1

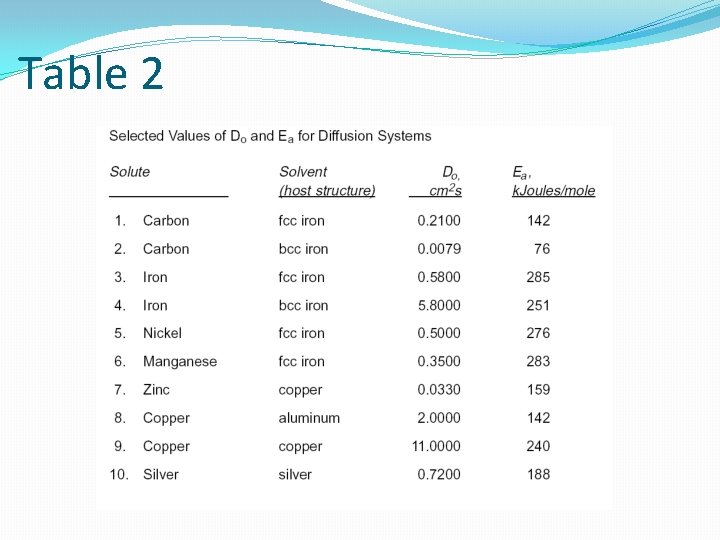
Table 2

First Fick’s Law �

Convection �

Stephan’s Flux �

Diffusion Flux �

Binary system �

Maxwell-Stefan formula �

Josef Stefan’s evaporation– diffusion tube � A vertical tube is partly filled with a liquid, which in turn evaporated and the vapor flowed out of the tube at the open end. � The tube portion above the liquid level contained a (binary) mixture consisting of the surrounding gas (air) and the vapor, generated on the liquid– gas interface. � Due to evaporation, the liquid level fell, and the process was unsteady, even if all other parameters were kept constant. � Under these conditions, Stefan derived equations for calculating the concentration distribution along tube length and the evaporation rate of the liquid.

The Stefan solution (1) � Stefan started by applying the momentum and continuity equations to diffusion in the gaseous area above the liquid level. The gas mixture and its components were treated as ideal gases, and the total pressure and temperature are constant through out the whole system. The origin of the coordinate x is the plane of the upper tube end, and the position of the liquid level is denoted by L. The gas mixture contained two components, and the Stefan equations describing the diffusion process are: 0 (14) (15) The indices 1 and 2 refer to the mixture components 1(vapor) and 2 (gas); t is the time, while A 12 and A 21 represent the resistance coefficients.

The Stefan solution (2) � Adding equations (15) and accounting (16): � Adding equations (14): (16) (17) 0 (18) 2 G � Adding equations (18): and considering that the interface is impermeable to gas(component 2) and the liquid does not move, so c 2 L=0, and u 1 L =0 , hence (19)

Boundary condition (17) � Eq. (14) for component 1 is written as: (20) � And substituting c 2 u 2 term from (20) � We can rewrite (14) as: (21) where, for reason of simplicity we have omitted some indices, and set: Note that Eq. (20) is obtained from the boundary conditions at the interface, but due to Eq. (17) it is valid in the whole diffusion space.

The Stefan solution (3) (21) (15) � Differentiating Eq. (21) with respect to x and combining with Eq. (15) for component 1 gives the relation : (21 a) With the boundary conditions: (22) This is known as the non-stationary Stefan diffusion equation

Additional Boundary Conditions (21) (22) (20) (23) (24) (25)

The Stefan solution (4) So we have: (21) (25) 0 Stefan gave the solution of Eq. (21) in the form: (26) where the constants B and a are to be determined from the boundary conditions at x=L, and (26) becomes: and with (25) And thus (27)

The Stefan solution (4) So we have: (27) Stefan then proceeded to discuss the case when the molar liquid density was much larger than the gas density, namely, c. L>>c, and b=(c. L-c)/c becomes very large. He simplified the integral (27), From this equation the following expression for the position of the interface was deduced : (27) Stefan compared this expression with an expression he derived in an earlier paper (Stefan, 1873) under the assumption of a constant evaporation rate (fixed interface): (28) Eq. (27) rests on the assumption c 10=0, that is, p 10=0. Assuming in this equation c. L>>c 1 L, c. L>>c 1 I, it becomes identical with Eq. (28).

Slattery & Mhetar Solution � Let us consider a vertical tube, partially filled For simplicity, let us replace the finite with a pure liquid A. gas phase with a semi-infinite gas that occupies all space corresponding to z 2 > 0: � For time t < 0, this liquid is isolated from the Z 2 remainder of the tube, which is filled with a at t =0 for all z 2 > 0: gas mixture of A and B, by a closed diaphragm. G(gas) � The entire apparatus is maintained at a X (A)=X (Ao) (1) constant temperature and pressure (neglecting the very small hydrostatic effect). X (A) - mole fraction of species A � At time t = 0, the diaphragm is carefully in the gas phase; opened, and the evaporation of A commences. X (Ao) - initial mole fraction of � Let us assume that A and B form an ideal-gas species A in the gas phase mixture. This allows us to say that the molar density c in gas phase is a constant 0 The liquid gas phase interface Z 3 throughout the gas phase. is a moving plane � We also assume that B is insoluble in A. Z 2 = h(t) (2) � We wish to determine the concentration L(liquid) distribution of A in the gas phase as well as the and at z 2 = h for all t > 0: position of the liquid-gas phase interface as functions of time. X(A)= X(A)e q. (3)

Slattery & Mhetar Solution (2) Equations (1) and (2) suggest that we seek a solution to this problem of the form V 1= V 3 =0 V 2= V 2 (t, z 2) (4) X(A)= X (A)(t, Z 2). V - molar averaged velocity of gas phase; V 2 - Z 2 component of the molar averaged velocity of gas phase. Since c can be taken to be a constant and since there is no homogeneous chemical reaction, the overall differential mass balance requires: Z 2 G(gas) V 2 0 U 2 L(liquid) Z 3

Slattery & Mhetar Solution (3) Z 2 G(gas) V 2 0 U 2 L(liquid) Z 3

Slattery & Mhetar Solution (3)

Slattery & Mhetar Solution (3)

Slattery & Mhetar Solution (4)

Solution (5)

Solution (6) (21)

Notes: (21) � (22)

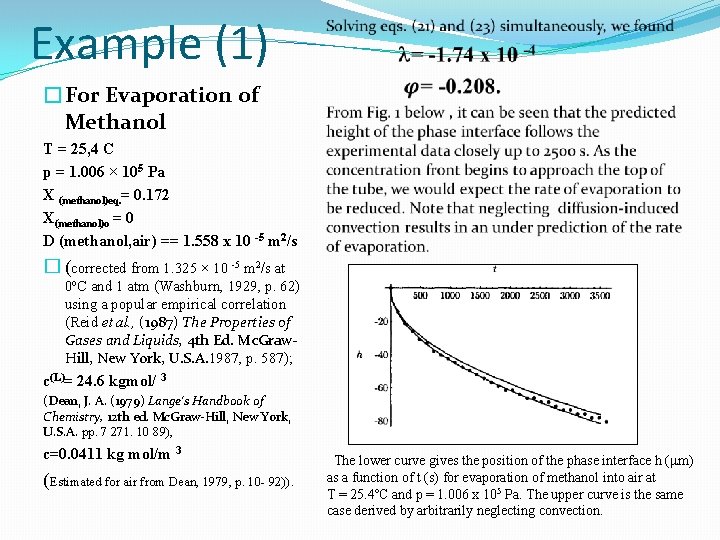
Example (1) �For Evaporation of Methanol T = 25, 4 C p = 1. 006 × 105 Pa X (methanol)eq. = 0. 172 X(methanol)o = 0 D (methanol, air) == 1. 558 x 10 -5 m 2/s � (corrected from 1. 325 × 10 -5 m 2/s at 0ºC and 1 atm (Washburn, 1929, p. 62) using a popular empirical correlation (Reid et al. , (1987) The Properties of Gases and Liquids, 4 th Ed. Mc. Graw. Hill, New York, U. S. A. 1987, p. 587); c(L)= 24. 6 kgmol/ 3 (Dean, J. A. (1979) Lange's Handbook of Chemistry, 12 th ed. Mc. Graw-Hill, New York, U. S. A. pp. 7 271. 10 89), c=0. 0411 kg mol/m 3 (Estimated for air from Dean, 1979, p. 10 - 92)). The lower curve gives the position of the phase interface h (mm) as a function of t (s) for evaporation of methanol into air at T = 25. 4ºC and p = 1. 006 x 105 Pa. The upper curve is the same case derived by arbitrarily neglecting convection.

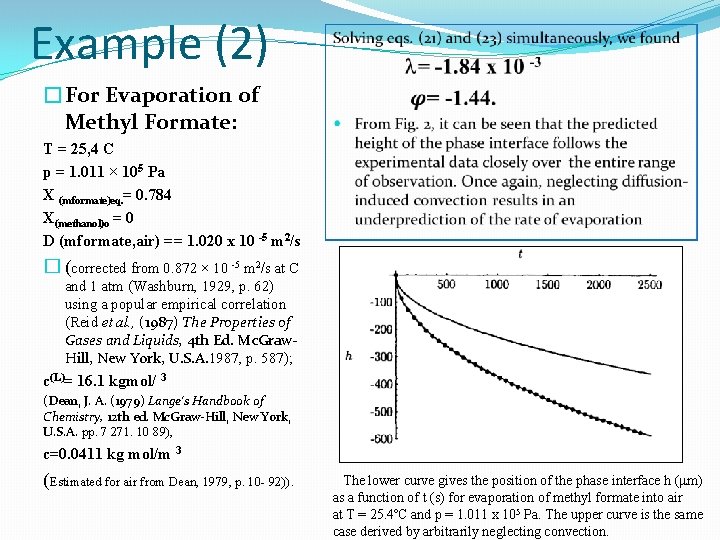
Example (2) �For Evaporation of Methyl Formate: T = 25, 4 C p = 1. 011 × 105 Pa X (mformate)eq. = 0. 784 X(methanol)o = 0 D (mformate, air) == 1. 020 x 10 -5 m 2/s � (corrected from 0. 872 × 10 -5 m 2/s at C and 1 atm (Washburn, 1929, p. 62) using a popular empirical correlation (Reid et al. , (1987) The Properties of Gases and Liquids, 4 th Ed. Mc. Graw. Hill, New York, U. S. A. 1987, p. 587); c(L)= 16. 1 kgmol/ 3 (Dean, J. A. (1979) Lange's Handbook of Chemistry, 12 th ed. Mc. Graw-Hill, New York, U. S. A. pp. 7 271. 10 89), c=0. 0411 kg mol/m 3 (Estimated for air from Dean, 1979, p. 10 - 92)). The lower curve gives the position of the phase interface h (mm) as a function of t (s) for evaporation of methyl formate into air at T = 25. 4ºC and p = 1. 011 x 105 Pa. The upper curve is the same case derived by arbitrarily neglecting convection.