Diffusion Diffusion Diffusion is defined as a process

Diffusion

Diffusion • Diffusion is defined as a process of mass transfer of individual molecules of a substance brought about by random molecular motion and associated with a driving force such as a concentration gradient. • The passage of matter through a solid barrier occur by: 1. simple molecular permeation (Molecular diffusion) through nonporous media 2. movement through pores and channels.

• • simple molecular permeation (Molecular diffusion) through nonporous media depends on the solubility of the permeating molecules in the bulk membrane. The transport of a drug through a polymeric membrane involves dissolution of the drug in the matrix of the membrane

movement through pores and channels • involve passage of a substance through solventfilled pores of a membrane • influenced by the relative size of the penetrating molecules and the diameter and shape of the pores. drug and solvent transport across the skin. through hair follicles, sebum ducts, and sweat pores in the epidermis

Diffusion • The mass transfer of a solvent (e. g. , water) or a solute (e. g. , a drug) forms the basis for many important phenomena in the pharmaceutical sciences, for example: 1. Diffusion of a drug across a biologic membrane is required for a drug to be absorbed into and eliminated from the body, and even for it to get to the site of action within a particular cell. 2. On the negative side, the shelf life of a drug product could be significantly reduced if a container or closure does not prevent solvent or drug loss or if it does not prevent the absorption of water vapor into the container. 6

Pharmaceutically important diffusion-based processes • Drug Absorption and Elimination • Diffusion through biologic membranes is an essential step for drugs entering (i. e. , absorption) or leaving (i. e. , elimination) the body. • It is also an important component along with convection for efficient drug distribution throughout the body and into tissues and organs. • Diffusion can occur through the lipoidal bilayer of cells. This is termed transcellular diffusion. On the other hand, paracellular diffusion occurs through the spaces between adjacent cells. • In addition to diffusion, drugs and nutrients also traverse biologic membranes using membrane transporters and, to a lesser extent, cell surface receptors. 7

Pharmaceutically important diffusion-based processes • Elementary Drug Release • Elementary drug release is an important process that literally affects nearly every person in everyday life. • Drug release is a multistep process that includes diffusion, disintegration, deaggregation, and dissolution. 8

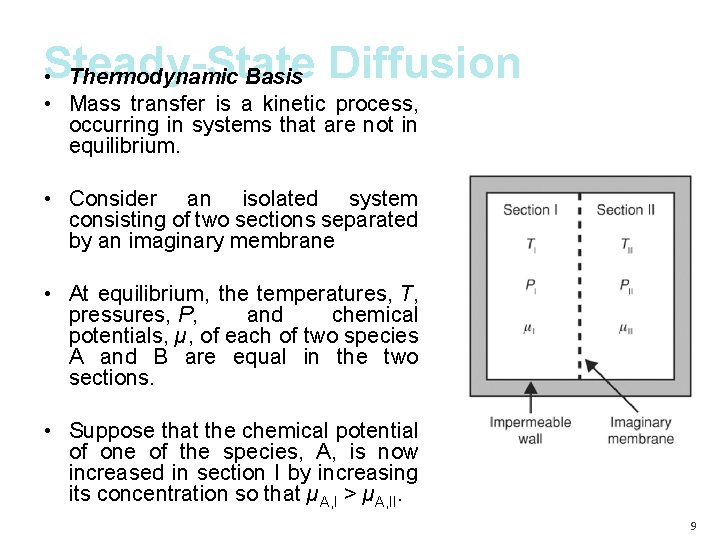
Steady-State • Thermodynamic Basis Diffusion • Mass transfer is a kinetic process, occurring in systems that are not in equilibrium. • Consider an isolated system consisting of two sections separated by an imaginary membrane • At equilibrium, the temperatures, T, pressures, P, and chemical potentials, µ, of each of two species A and B are equal in the two sections. • Suppose that the chemical potential of one of the species, A, is now increased in section I by increasing its concentration so that µA, I > µA, II. 9

• Thermodynamic Basis • The system will respond to this perturbation by establishing a new thermodynamic equilibrium. • If the membrane separating the two sections will allow for the passage of species A, then equilibrium will be reestablished by the movement of species A from section I to section II until the chemical potentials of section I and II are once again equal. • The movement of mass in response to a spatial gradient in chemical potential as a result of random molecular motion (i. e. , Brownian motion) is called diffusion. 10

Fick's Laws of Diffusion Fick’s first law • The amount, M, of material flowing through a unit area, S, of a barrier in unit time, t, is known as the flux, J: • The flux, in turn, is proportional to the concentration gradient, d. C/dx: Fick's first law • D is the diffusion coefficient of a penetrant (diffusant) in cm 2/sec, • C is its concentration in g/cm 3, • x is the distance in centimeter of movement perpendicular to the surface of the barrier. 11

Fick's Laws of Diffusion Fick’s first law • The negative sign of equation signifies that diffusion occurs in a direction opposite to that of increasing concentration. • That is, diffusion occurs in the direction of decreasing concentration of diffusant; thus, the flux is always a positive quantity. • Diffusion will stop when the concentration gradient no longer exists (i. e. , when d. C/dx = 0). 12

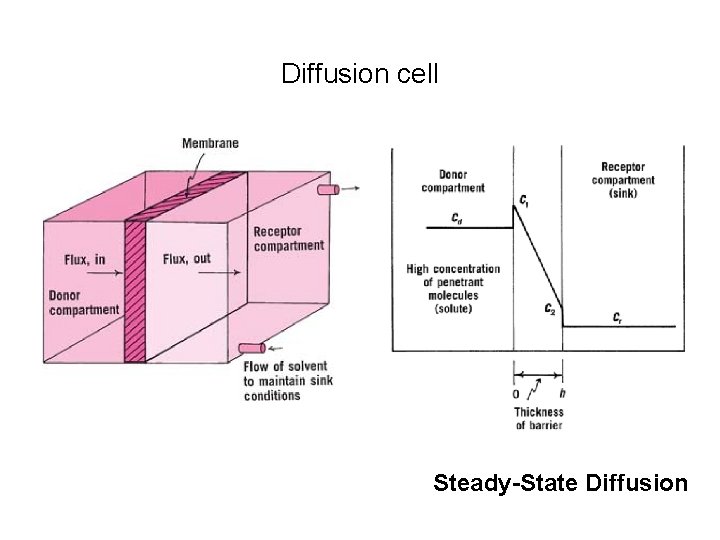
Diffusion cell Steady-State Diffusion

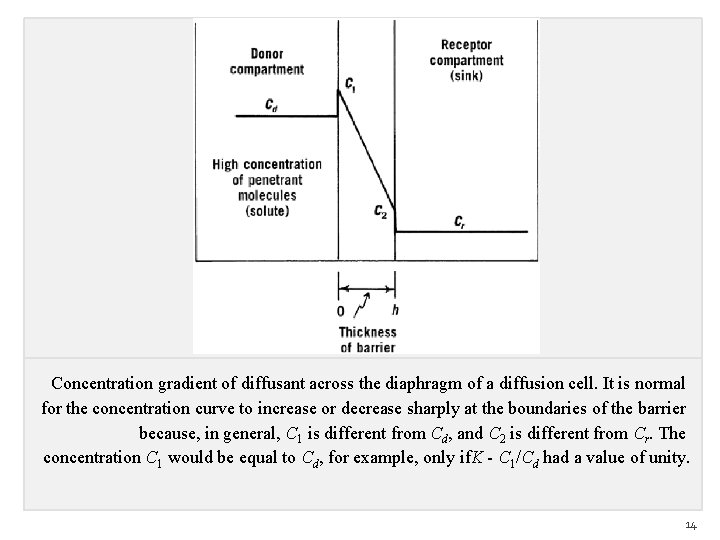
Concentration gradient of diffusant across the diaphragm of a diffusion cell. It is normal for the concentration curve to increase or decrease sharply at the boundaries of the barrier because, in general, C 1 is different from Cd, and C 2 is different from Cr. The concentration C 1 would be equal to Cd, for example, only if. K - C 1/Cd had a value of unity. 14

Steady State • Consider the diffusant ( drug) originally dissolved in a solvent in the donor compartment Cd of the chamber. • Solvent alone is placed on the receptor Cr. • the solute or penetrant diffuses through the central barrier from solution to solvent side (donor to receptor compartment).

• In diffusion experiments, the solution in the receptor compartment is constantly removed and replaced with fresh solvent to keep the concentration at a low level in receptor compartment. • This is referred to as “sink conditions, ” the donor compartment being the source and the receptor compartment the sink. • When the system has been in existence a sufficient time, the concentration of diffusant in the solutions at the left and right of the barrier becomes constant with respect to time but obviously not the same in the two compartments. “Steady State conditions, ”

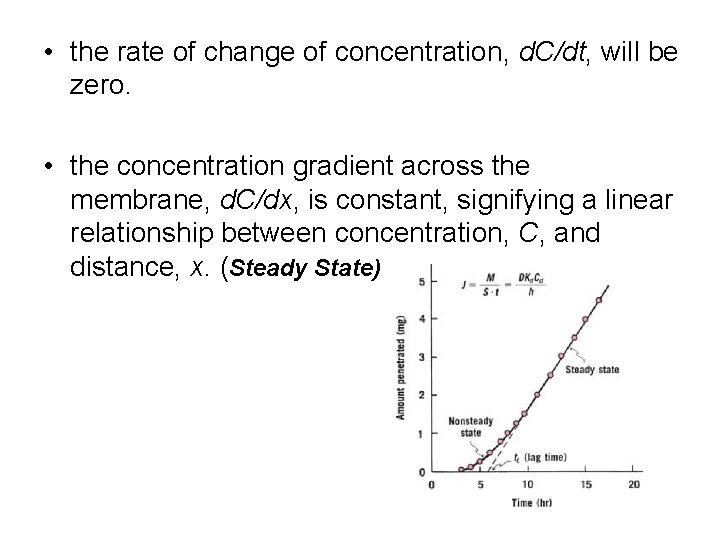
• the rate of change of concentration, d. C/dt, will be zero. • the concentration gradient across the membrane, d. C/dx, is constant, signifying a linear relationship between concentration, C, and distance, x. (Steady State)

Fick's Laws of Diffusion Fick’s second law • An equation for mass transport that emphasizes the change in concentration with time at a definite location (rather than unit area of barrier) in unit time is known as Fick's second law. D is the diffusion coefficient of a penetrant (diffusant) in cm 2/sec, C is its concentration in g/cm 3, x is the distance in centimeter of movement perpendicular to the surface of the barrier. the mass, M, is usually given in grams or moles, the barrier surface area, S, in cm 2, the time, t, in seconds. The units of J are g/cm 2 sec. 18

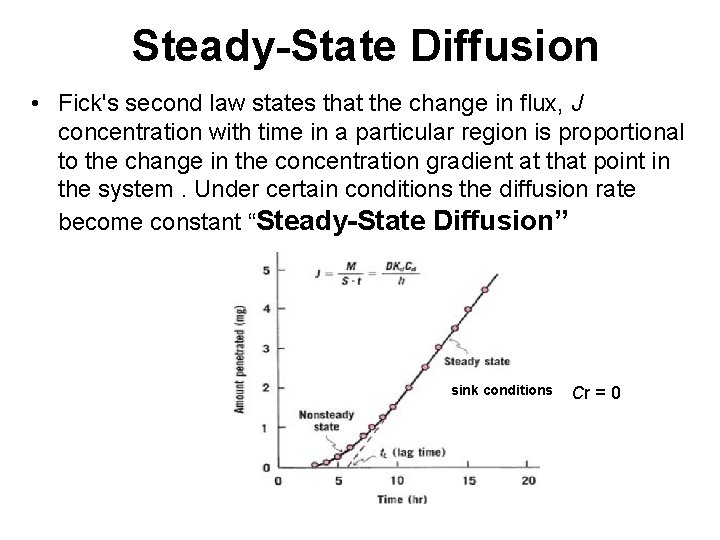
Steady-State Diffusion • Fick's second law states that the change in flux, J concentration with time in a particular region is proportional to the change in the concentration gradient at that point in the system. Under certain conditions the diffusion rate become constant “Steady-State Diffusion” sink conditions Cr = 0

• if sink conditions hold in the receptor compartment, Cr [congruent] 0,

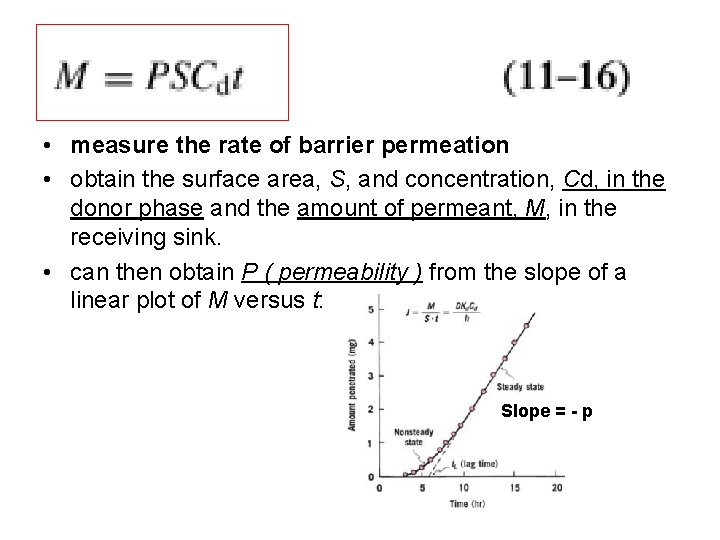
• measure the rate of barrier permeation • obtain the surface area, S, and concentration, Cd, in the donor phase and the amount of permeant, M, in the receiving sink. • can then obtain P ( permeability ) from the slope of a linear plot of M versus t: Slope = - p

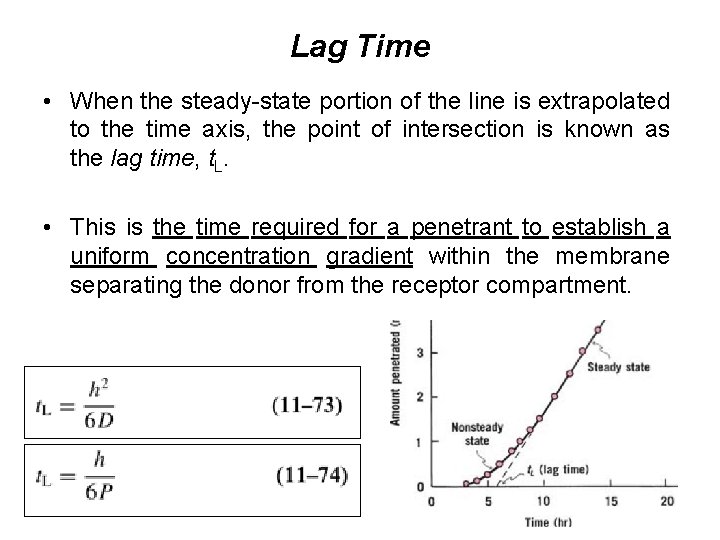
Lag Time • When the steady-state portion of the line is extrapolated to the time axis, the point of intersection is known as the lag time, t. L. • This is the time required for a penetrant to establish a uniform concentration gradient within the membrane separating the donor from the receptor compartment.

Home work A drug is allowed to pass through a semiperamble membrane having a cross –section area , S, of 10. 36 cm 2 and a thickness , h, of 0. 085 cm in a diffusion cell at 25°C , From the horizontal intersecept of a plot of amount of drug diffuses , M , versus time , t, , the Lag time , t. L , is found to be 47. 5 min. the original concentration C 0 is 0. 003 mmol/cm 3, the permeability is 6. 1 x 10 -4. – Calculate the Diffusion coefficent , D, using lag time ? – Calculate the Partion coefficent , K ?