Diffuse Reflection Imaging Earthshine and other Faint Signals

Diffuse Reflection Imaging: Earthshine and other Faint Signals Sam Hasinoff MIT CSAIL, TTIC, Google[x] Samuel W. Hasinoff, Anat Levin, Philip R. Goode, and William T. Freeman, Diffuse Reflectance Imaging with Astronomical Applications, Proc. 13 th IEEE International Conference on Computer Vision, ICCV 2011 http: //people. csail. mit. edu/hasinoff/diffuse/

2 Joint work with: Bill Freeman MIT CSAIL Anat Levin Weizmann Institute Special thanks to: Philip Goode Big Bear Solar Observatory Bernhard Schölkopf, Frédo Durand, Livia Illie, David Chen

Indirect Imaging with Reflective Objects specular reflectance glossy reflectance diffuse reflectance virtual camera bad camera? really bad camera? 3

Resolution of a Diffuse Reflector Diffuse surfaces blur together incident lighting from many directions 1 0 -180° 0° +180° Lambertian reflectance How much detail can we resolve? 4

5 Single-Bounce Light Transport reflected radiance surface incoming visibility albedo radiance BRDF clipped cosine 1 reflectance = (albedo. lighting) 0 -180° BRDF * for convex objects, distant illumination 0° +180°

6 Linear Light Transport Usual matrix formulation observed pixels transfer distant matrix lighting transfer matrix encodes geometry, BRDF, surface albedo noise

Resolution of a Diffuse Reflector about 9 pixels? images of a convex Lambertian objects with distant lighting lie in a 9 D subspace (<2% average error) [Basri and Jacobs, 2001] [Ramamoorthi and Hanrahan, 2001] … e. g. lighting-insensitive recognition with 9 basis images 7

Key: Occlusion Geometry Codes Illumination convex about 9 pixels? self-occlusion potentially much better 8

Key: Occlusion Geometry Codes Illumination What 3 D shape lets us best resolve the lighting? convex about 9 pixels? self-occlusion potentially much better 9

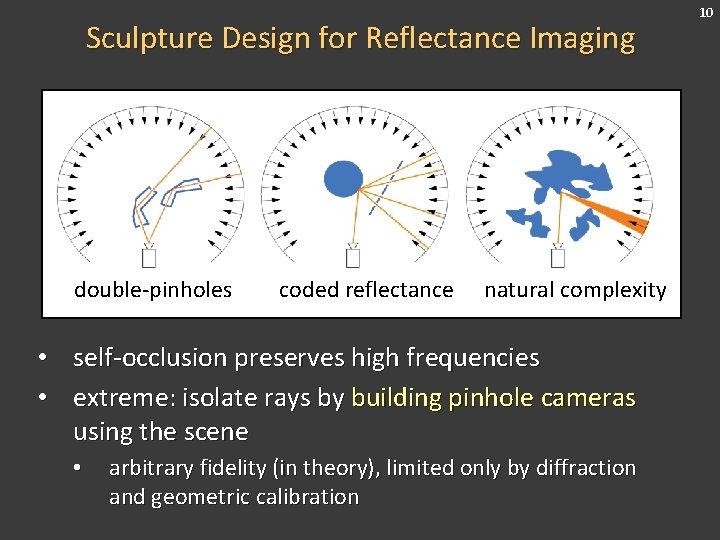
Sculpture Design for Reflectance Imaging double-pinholes coded reflectance natural complexity • self-occlusion preserves high frequencies • extreme: isolate rays by building pinhole cameras using the scene • arbitrary fidelity (in theory), limited only by diffraction and geometric calibration 10

Bayesian Reconstruction Method Standard MAP estimation • Gaussian prior [Wiener 1949] • Sparse derivative prior [Levin et al. 2007] 11

Reconstructing a Changing Target For time-varying lighting, reconstruct stable part • marginalize out temporal variations temporal binning with Gaussian prior temporal variations as correlated noise 12

Approach #1: Rim Reflectance Imaging Exploit visibility changes near occlusion boundary • works for compact lighting, e. g. object lit head on • multiple orientations = tomography + single shot enough - need high resolution - need accurate geometry not previously used in astronomy or computer vision 13

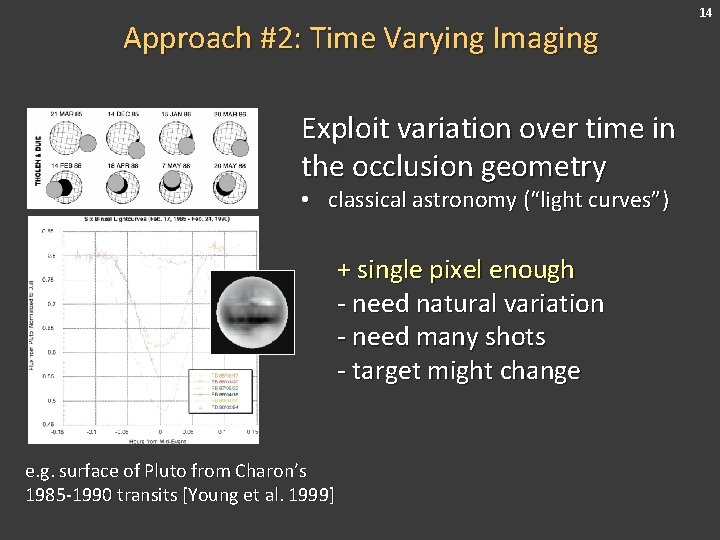
Approach #2: Time Varying Imaging Exploit variation over time in the occlusion geometry • classical astronomy (“light curves”) + single pixel enough - need natural variation - need many shots - target might change e. g. surface of Pluto from Charon’s 1985 -1990 transits [Young et al. 1999] 14

Earth from Space from Earth - Feasibility Study Earth from Apollo 17, 1972 (NASA) 15

Low-Resolution Expectations NASA’s “Blue Planet” reconstruction we’d be happy with 16

Moon as Earth Reflector (“Earthshine”) Leonardo Da Vinci’s Codex Leicester (ca. 1510) 17

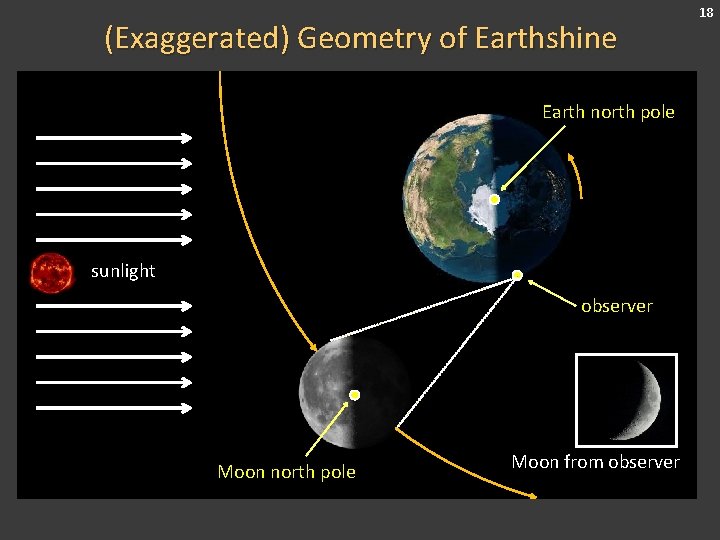
(Exaggerated) Geometry of Earthshine Earth north pole sunlight observer Moon north pole Moon from observer 18

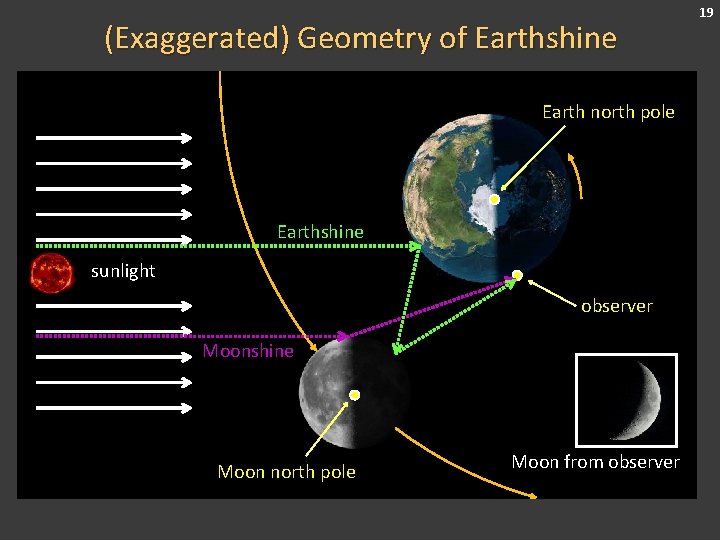
(Exaggerated) Geometry of Earthshine Earth north pole Earthshine sunlight observer Moonshine Moon north pole Moon from observer 19

Integrating over Earth from the Moon albedo of “unknown” Earth patch cos(incoming) cos(outgoing) Earth phase (≈ 180° - Moon phase) Earth integrand, from point on the Moon (simulation) Aug 8, 2010, 5 am Feb 24, 2010, 1 am 20

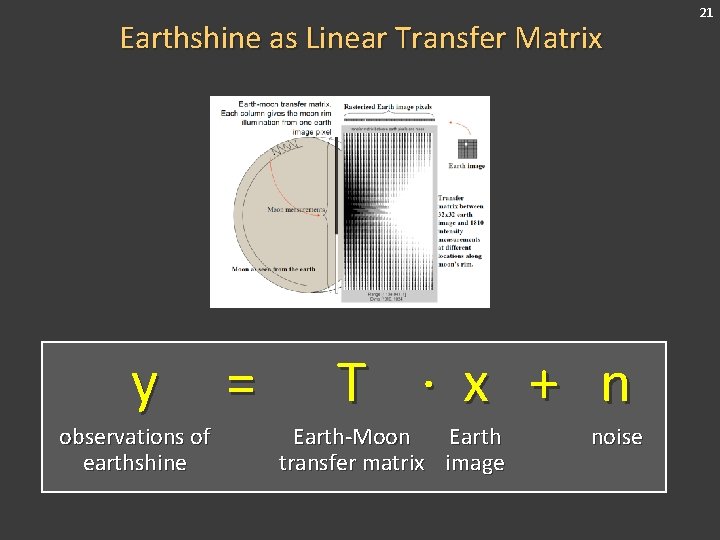
Earthshine as Linear Transfer Matrix y observations of earthshine = T ∙ x + n Earth-Moon Earth transfer matrix image noise 21

Recipe for Earthshine Imaging feasible observing times: • moon >2° above horizon • moon <85% full • sun >8° below horizon • clear skies (air mass) (moonshine) (twilight) track moon - multi-minute exposures > -2. 5 app. mag. (V) block moonshine glare with occluder BBSO [Qiu et al. 2003] 22

Approach #1: Visibility at Moon Rim • From rim of Moon, different Earth regions visible • Special challenges: • need very high resolution, SNR • need detailed moon topography • BRDF at grazing angles? Earthrise, as seen from Apollo 8 (NASA) 23

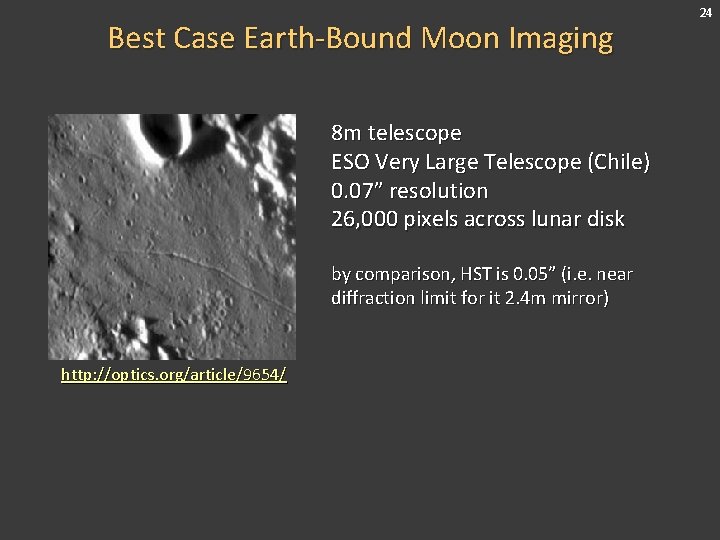
Best Case Earth-Bound Moon Imaging 8 m telescope ESO Very Large Telescope (Chile) 0. 07” resolution 26, 000 pixels across lunar disk by comparison, HST is 0. 05” (i. e. near diffraction limit for it 2. 4 m mirror) http: //optics. org/article/9654/ 24

Sampling the Earth and Moon Surface moon simulation, 2475 samples (55 per radial line) ground truth earth model (75 x 30 pixels) relative contribution, Lambertian Earth 25

sparse prior reconstruction 80 d. B 60 d. B 40 d. B Simulated Reconstruction for Single Shot std. optics (0. 4”) adaptive optics (0. 07”) 26

Approach #2: Scanning over Time • Over time, Earth region visible to Moon & Sun changes • Single pixel observations is fine • Special challenges: • 1 D set of viewpoints per day • time varying cloud cover, snow, etc. 1 am, Feb 24, 2010 5 am, Feb 24, 2010 2 am, Aug 14, 2010 region of Earth visible from Moon’s disk, i. e. contributing to earthshine 27

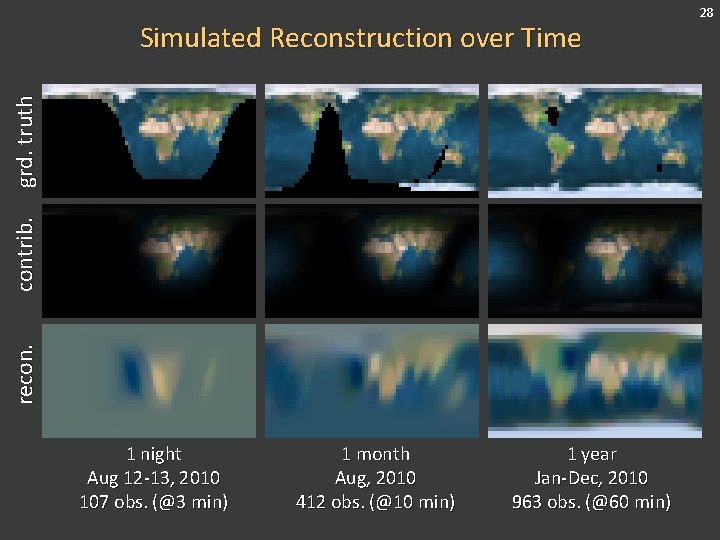
recon. contrib. grd. truth Simulated Reconstruction over Time 1 night Aug 12 -13, 2010 107 obs. (@3 min) 1 month Aug, 2010 412 obs. (@10 min) 1 year Jan-Dec, 2010 963 obs. (@60 min) 28

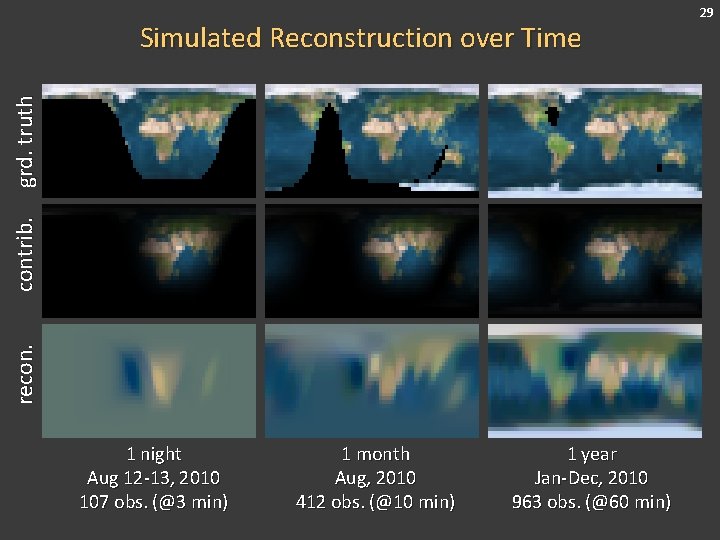
recon. contrib. grd. truth Simulated Reconstruction over Time 1 night Aug 12 -13, 2010 107 obs. (@3 min) 1 month Aug, 2010 412 obs. (@10 min) 1 year Jan-Dec, 2010 963 obs. (@60 min) 29

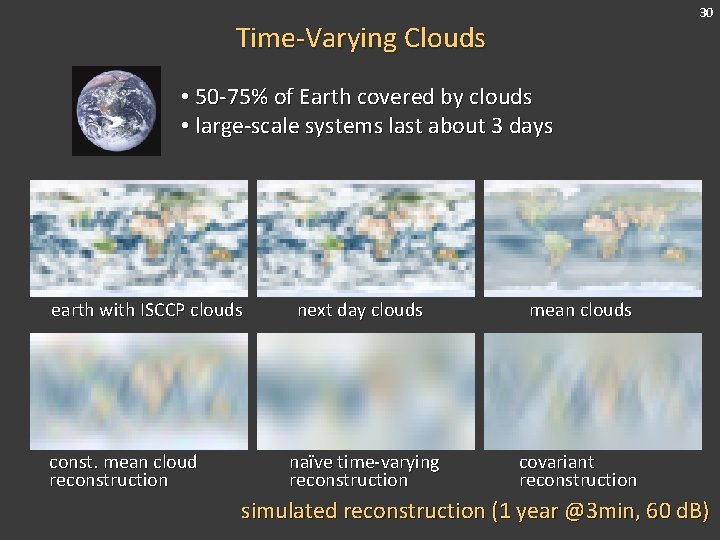
30 Time-Varying Clouds • 50 -75% of Earth covered by clouds • large-scale systems last about 3 days earth with ISCCP clouds const. mean cloud reconstruction next day clouds mean clouds naïve time-varying reconstruction covariant reconstruction simulated reconstruction (1 year @3 min, 60 d. B)

Reconstructing Mars from Light Curves • direct observation • outer planet, so less phase change (>85% disk lit) • much less active weather than earth • axial tilt of 25° (2 D directions) • more Lambertian? Martian surface 31

Martian Reconstruction from Historical Spectra ground truth + visibility recon. from simulation (scaled) relative contribution recon. from real data (h. VB), 47 d. B 234 spectra (single-pixel images) observed at 2 sites, from 1963 -1965 [Irivine et al. 1968 ab] 32

Simulation: Limits of Single-Pixel Mars Reconstruction 200 samples 400 samples 800 samples 1600 samples 3200 samples 23731 samples 1 Martian year (= 2 years) single-pixel images, 60 d. B, no temporal variation 33

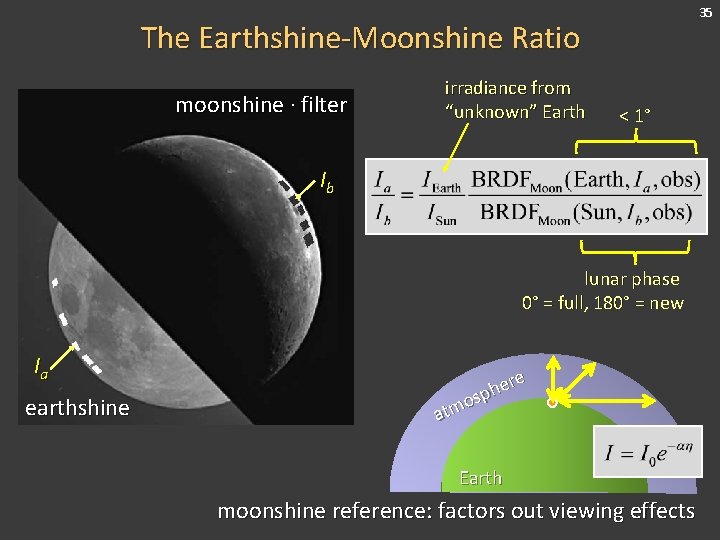
10 Years of Moon Photos moonshine ∙ filter Ib Ia earthshine Moon from BBSO [Qiu et al. 2003] • 10 years • 40 k+ photos • photos every 5 min • Big Bear Solar Observatory (BBSO), near LA • single CCD (grayscale) 34

35 The Earthshine-Moonshine Ratio moonshine ∙ filter irradiance from “unknown” Earth < 1° Ib lunar phase 0° = full, 180° = new Ia earthshine re e h sp o m at Earth moonshine reference: factors out viewing effects

Coda: Optimizing Capture Strategies • imaging tradeoffs, e. g. blur vs. noise • sensor characteristics vs. 2. 8 d. B 14. 6 d. B http: //people. csail. mit. edu/hasinoff/ 36