Diffraction Monday Nov 18 2002 1 Diffraction theory

Diffraction Monday Nov. 18, 2002 1

Diffraction theory (10. 4 Hecht) n We will first develop a formalism that will describe the propagation of a wave – that is develop a mathematical description of Huygen’s principle Wavefront U What is U here? We know this 2

Diffraction theory n n Consider two well behaved functions U 1’, U 2’ that are solutions of the wave equation. Let U 1’ = U 1 e-i t ; U 2’ = U 2 e-i t Thus U 1 , U 2 are the spatial part of the functions and since, we have, 3

Green’s theorem n Consider the product U 1 grad U 2 = U 1 U 2 Using Gauss’ Theorem n Where S = surface enclosing V n Thus, n 4

Green’s Theorem n Now expand left hand side, n Do the same for U 2 U 1 and subtract from (2), gives Green’s theorem 5

Green’s theorem n Now for functions satisfying the wave equation (1), i. e. n Consequently, n since the LHS of (3) = 0 6

Green’s theorem applied to spherical wave propagation n Let the disturbance at t=0 be, where r is measured from point P in V and U 1 = “Green’s function” Since there is a singularity at the point P, draw a small sphere P, of radius , around P (with P at centre) Then integrate over + P, and take limit as 0 7

Spherical Wave propagation P Thus (4) can be written, 8

Spherical Wave propagation n In (5), an element of area on P is defined in terms of solid angle n and we have used n Now consider first term on RHS of (5) 9

Kirchoff’s Integral Theorem n Now U 2 = continuous function and thus the derivative is bounded (assume) Its maximum value in V = C Then since eik 1 as 0 we have, n The second term on the RHS of (5) n n 10

Kirchoff’s Integral Theorem Now as 0 U 2(r) UP (its value at P) and, Now designate the disturbance U as an electric field E 11

Kirchoff integral theorem This gives the value of disturbance at P in terms of values on surface enclosing P. It represents the basic equation of scalar diffraction theory 12

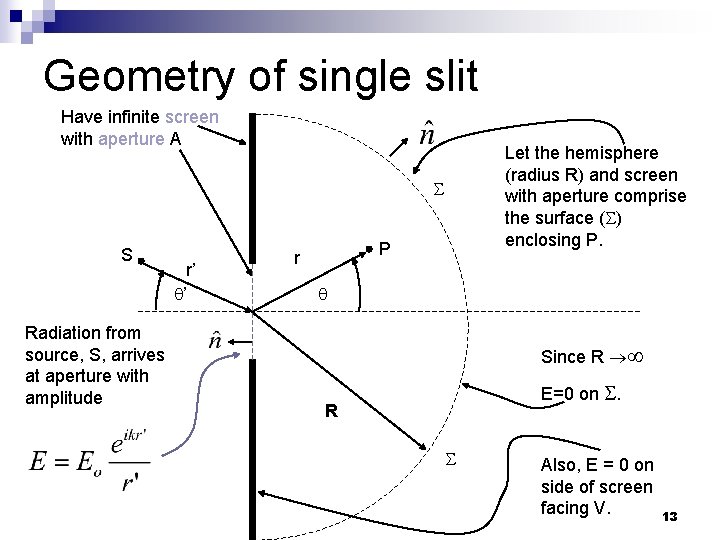
Geometry of single slit Have infinite screen with aperture A Let the hemisphere (radius R) and screen with aperture comprise the surface ( ) enclosing P. S Radiation from source, S, arrives at aperture with amplitude r’ ’ P r Since R E=0 on . R Also, E = 0 on side of screen facing V. 13

Fresnel-Kirchoff Formula n Thus E=0 everywhere on surface except the portion that is the aperture. Thus from (6) 14

Fresnel-Kirchoff Formula n n Now assume r, r’ >> ; then k/r >> 1/r 2 Then the second term in (7) drops out and we are left with, Fresnel Kirchoff diffraction formula 15

Obliquity factor Since we usually have ’ = - or n. r’=-1, the obliquity factor F( ) = ½ [1+cos ] n Also in most applications we will also assume that cos 1 ; and F( ) = 1 n For now however, keep F( ) n 16

Huygen’s principle n Amplitude at aperture due to source S is, n Now suppose each element of area d. A gives rise to a spherical wavelet with amplitude d. E = EAd. A n Then at P, n Then equation (6) says that the total disturbance at P is just proportional to the sum of all the wavelets weighted by the obliquity factor F( ) n This is just a mathematical statement of Huygen’s principle. 17

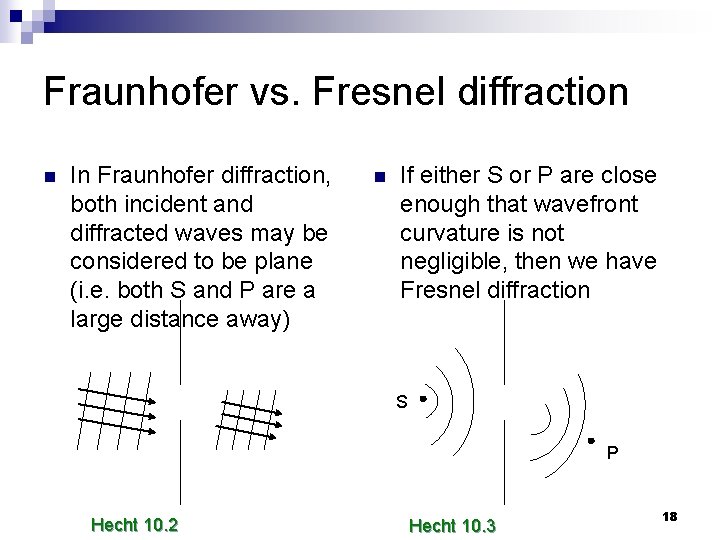
Fraunhofer vs. Fresnel diffraction n In Fraunhofer diffraction, both incident and diffracted waves may be considered to be plane (i. e. both S and P are a large distance away) n If either S or P are close enough that wavefront curvature is not negligible, then we have Fresnel diffraction S P Hecht 10. 2 Hecht 10. 3 18

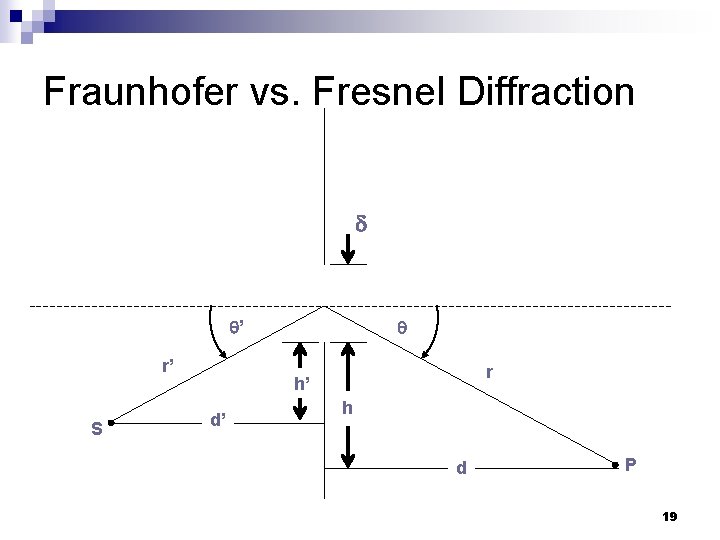
Fraunhofer vs. Fresnel Diffraction ’ r’ S r h’ d’ h d P 19

Fraunhofer Vs. Fresnel Diffraction Now calculate variation in (r+r’) in going from one side of aperture to the other. Call it 20

Fraunhofer diffraction limit n Now, first term = path difference for plane waves sin ’≈ h’/d’ sin ≈ h/d sin ’ + sin = ( h’/d + h/d ) Second term = measure of curvature of wavefront Fraunhofer Diffraction 21

Fraunhofer diffraction limit n n n If aperture is a square - X The same relation holds in azimuthal plane and 2 ~ measure of the area of the aperture Then we have the Fraunhofer diffraction if, Fraunhofer or far field limit 22

Fraunhofer, Fresnel limits n The near field, or Fresnel, limit is n See 10. 1. 2 of text 23

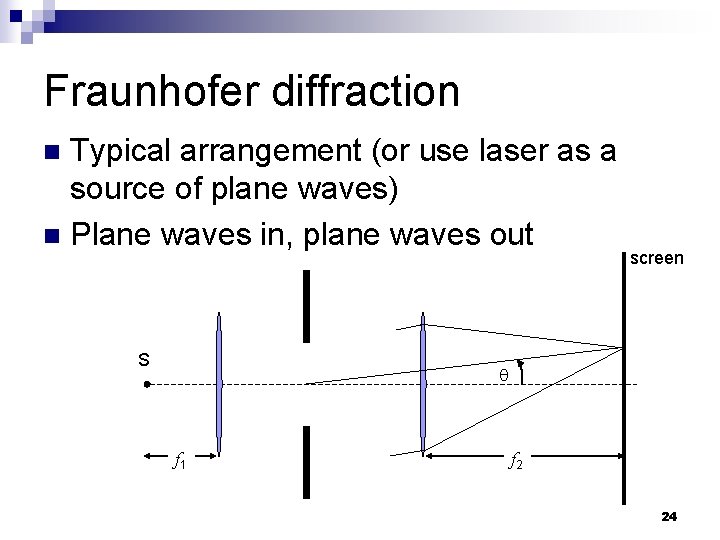
Fraunhofer diffraction Typical arrangement (or use laser as a source of plane waves) n Plane waves in, plane waves out n S screen f 1 f 2 24

Fraunhofer diffraction 1. 2. Obliquity factor Assume S on axis, so Assume small ( < 30 o), so Assume uniform illumination over aperture r’ >> so 3. is constant over the aperture Dimensions of aperture << r r will not vary much in denominator for calculation of amplitude at any point P consider r = constant in denominator 25

Fraunhofer diffraction n Then the magnitude of the electric field at P is, 26

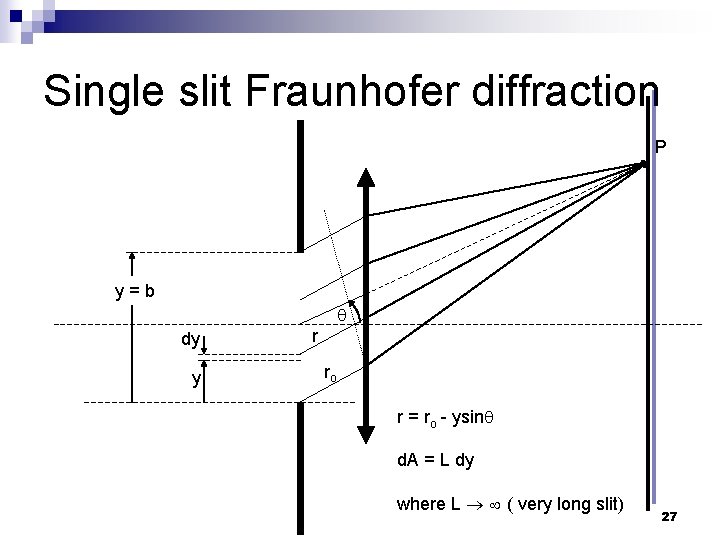
Single slit Fraunhofer diffraction P y=b dy y r ro r = ro - ysin d. A = L dy where L ( very long slit) 27

Single slit Fraunhofer diffraction Fraunhofer single slit diffraction pattern 28