Diffraction Grating The diffraction grating is working as

Diffraction Grating • The diffraction grating is working as yang's experiment. It is consist of thousand of lines (slits) in very small area the distance between those slits is the same width. The grating will for the bright and sharper diffraction pattern only. The ray of the diffraction grating is focused on the screen using a lens. The grating is a constrictive interference with first and second till forth order. Each order is less brightens than the higher and so on ( 1 st order > 2 nd order >3 rd >4 th ) • The condition formation the bright fringes in the diffraction is the same as young’s experiment. Therefore we can write the grating equation as. d sin qn = n l Where n = 1, 2, 3, 4, ……. The number of order not the fringes d = spacing of slits l = Wavelength of incident light qn = deviation angle for nth bright fringes 1 OPTO 356

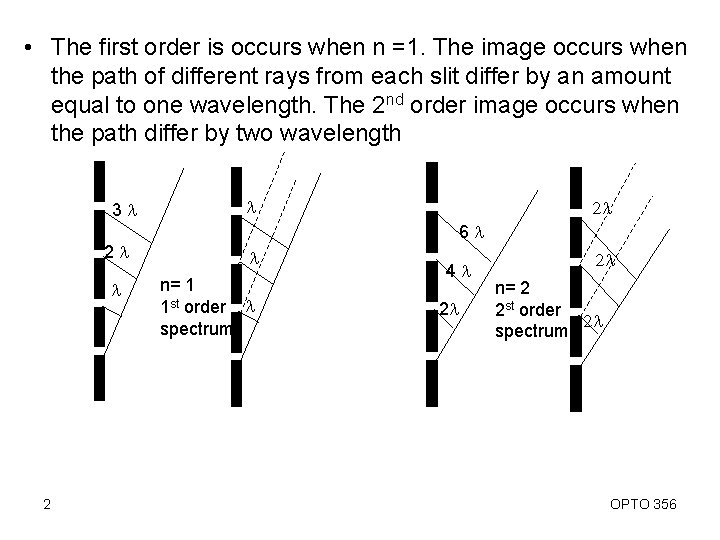
• The first order is occurs when n =1. The image occurs when the path of different rays from each slit differ by an amount equal to one wavelength. The 2 nd order image occurs when the path differ by two wavelength 3 l 2 l 1 l 2 l 2 l 6 l l n= 1 1 st order l spectrum 4 l 2 l 2 l n= 2 2 st order 2 l spectrum OPTO 356

Example • A diffraction grating having 20. 000 lines/in. is illuminated by parallel light of wavelength 589 nm. What are the angle at which the first order and second order bright fringes are formed? • Answer: • The slit spacing d that corresponds to 20, 000 lins/in is d = 2. 54 cm/in / 20, 000 lines/in = 1. 27 x 10 -4 cm The first order bright occurs at n =1 so sin q 1 = n l /d = 5. 89 x 10 -5 / 1. 27 x 10 -4 = 0. 464 q 1 = sin-1(0. 464) = 27. 6 o The Second order at n =2 sin q 2 = 2 x 0. 464 = 0. 928 q 2 = sin -1 (0. 928) = 68. 1 o The third order will not be formed because sin qn can not exceed 1 because the beam will not deviated by an angle greater than 90 o 3 OPTO 356

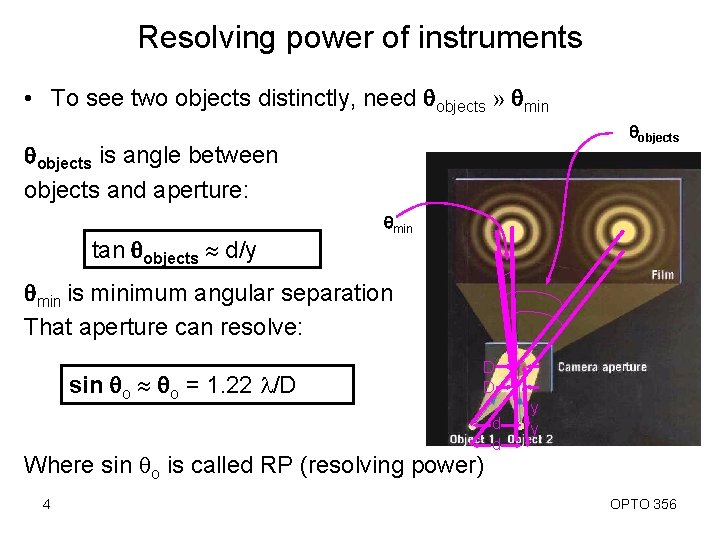
Resolving power of instruments • To see two objects distinctly, need qobjects » qmin qobjects is angle between objects and aperture: tan qobjects d/y qmin is minimum angular separation That aperture can resolve: sin qo = 1. 22 l/D D D Where sin qo is called RP (resolving power) 4 d d y y OPTO 356

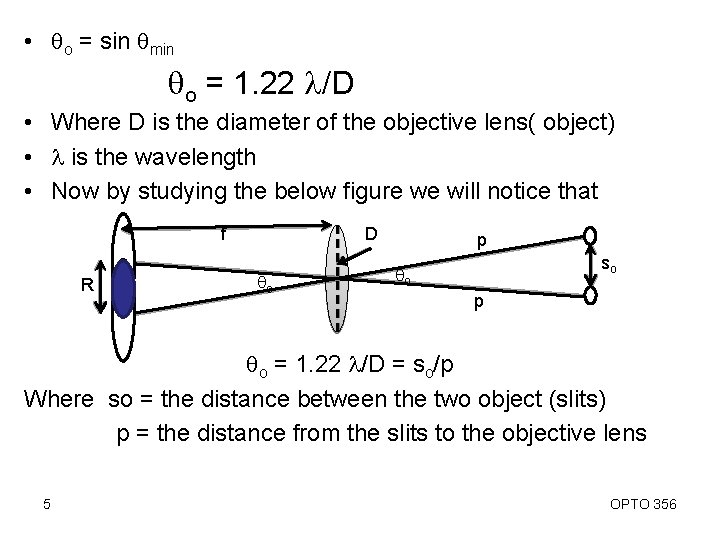
• qo = sin qmin qo = 1. 22 l/D • Where D is the diameter of the objective lens( object) • l is the wavelength • Now by studying the below figure we will notice that f R D qo p so qo p qo = 1. 22 l/D = so/p Where so = the distance between the two object (slits) p = the distance from the slits to the objective lens 5 OPTO 356

• To measured the radius of the center maximum in the diffraction pattern we use the focal point of the objective lens. R = f qo = f so/p Where f is the focal point • Notice • 1 - it should be have a distance between the two object to have resolving power • 2 - the distance between the two object will make an angle q between the interference of the two wave that coming from the two object • 3 - we have no distance between the two object we get a complete interference that make zero angle so we have no RP 6 OPTO 356

• One of the largest refracting telescope in the world is the 40 in diameter instrument at yerkes Observatory in Wisconsin; its objective lens has a focal length of 19. 8 m (65 ft). • a) What is the minimum separation of two features of the moon’s surface such that they are just resolved by this telescope? • b) What is the radius of the center maximum in the diffraction pattern set up by the objective lens? (For white light, the central wavelength of 500 nm can be used for computing the resolution. The moon is 3. 84 x 105 km from the earth • The solution p = 3. 84 x 105 km = 3. 84 x 108 m l = 500 nm = 500 x 10 -9 = 5 x 10 -7 m D = 40 in = 40 x 2. 54 x 10 -2 = 1. 02 m 7 OPTO 356

p = 3. 84 x 105 km = 3. 84 x 108 m l = 500 nm = 500 x 10 -9 = 5 x 10 -7 m D = 40 in = 40 x 2. 54 x 10 -2 = 1. 02 m This minimum separation distance so is determine by qo = 1. 22 l / D = so/p so = 1. 22 l p / D so = 1. 22 x 5 x 10 -7 x 3. 84 x 108/ 1. 02 so = 230 m R = f so/p R = 19. 8 x 230 / 3. 84 x 108 R = 1. 19 x 10 -5 m The 200 in reflecting telescope at Mt. Palomar in California can distinguish features on the moon 46. 3 m (or 152 ft) apart 8 OPTO 356

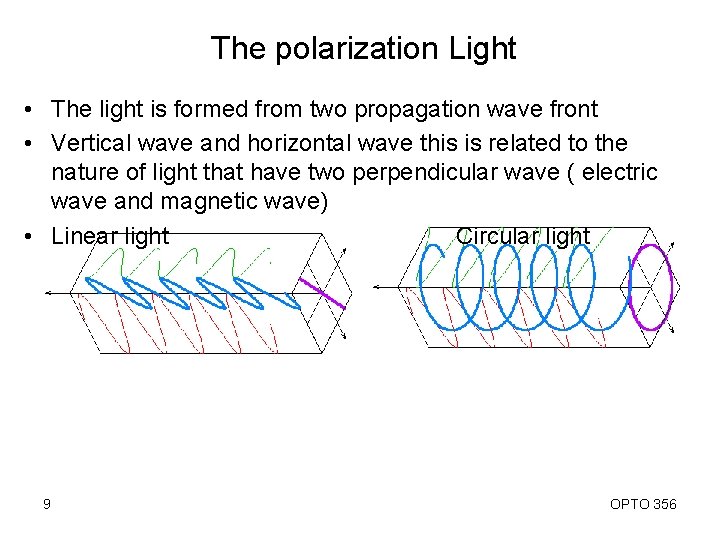
The polarization Light • The light is formed from two propagation wave front • Vertical wave and horizontal wave this is related to the nature of light that have two perpendicular wave ( electric wave and magnetic wave) • Linear light Circular light 9 OPTO 356

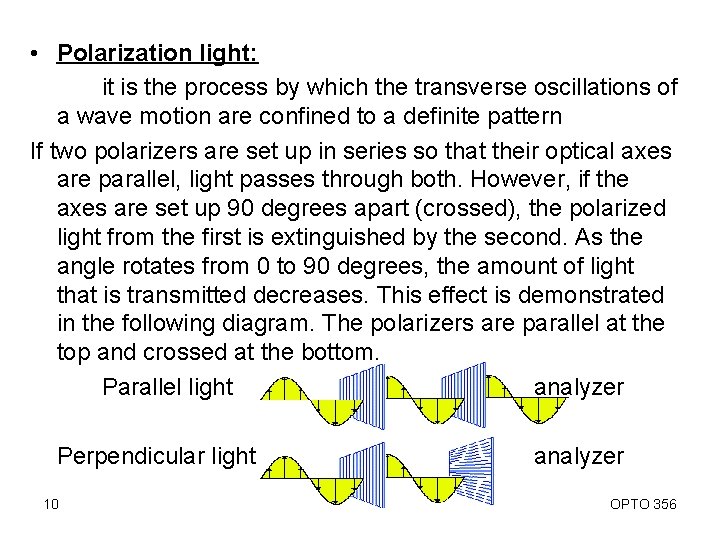
• Polarization light: it is the process by which the transverse oscillations of a wave motion are confined to a definite pattern If two polarizers are set up in series so that their optical axes are parallel, light passes through both. However, if the axes are set up 90 degrees apart (crossed), the polarized light from the first is extinguished by the second. As the angle rotates from 0 to 90 degrees, the amount of light that is transmitted decreases. This effect is demonstrated in the following diagram. The polarizers are parallel at the top and crossed at the bottom. Parallel light analyzer Perpendicular light 10 analyzer OPTO 356

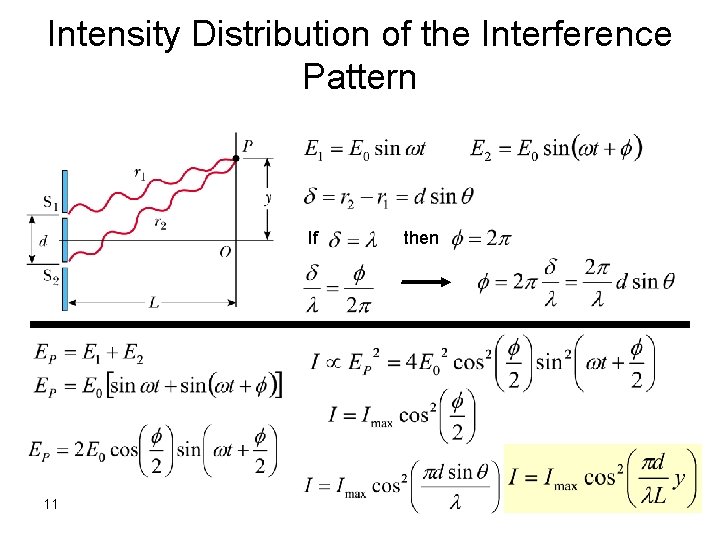
Intensity Distribution of the Interference Pattern If 11 then OPTO 356

• Interference depends on the relative phase of the two waves. • It also depends on the path difference between them. • The resultant intensity at a point is proportional to the square of the resultant electric field at that point. not 12 OPTO 356

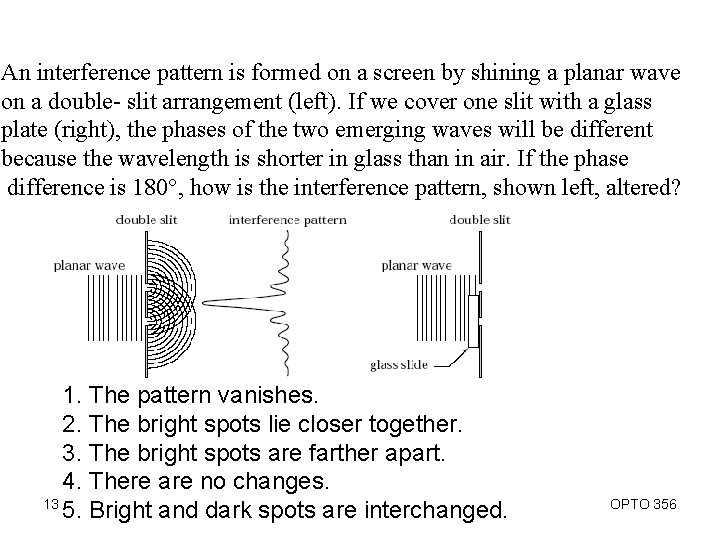
An interference pattern is formed on a screen by shining a planar wave on a double- slit arrangement (left). If we cover one slit with a glass plate (right), the phases of the two emerging waves will be different because the wavelength is shorter in glass than in air. If the phase difference is 180°, how is the interference pattern, shown left, altered? 1. The pattern vanishes. 2. The bright spots lie closer together. 3. The bright spots are farther apart. 4. There are no changes. 13 5. Bright and dark spots are interchanged. OPTO 356

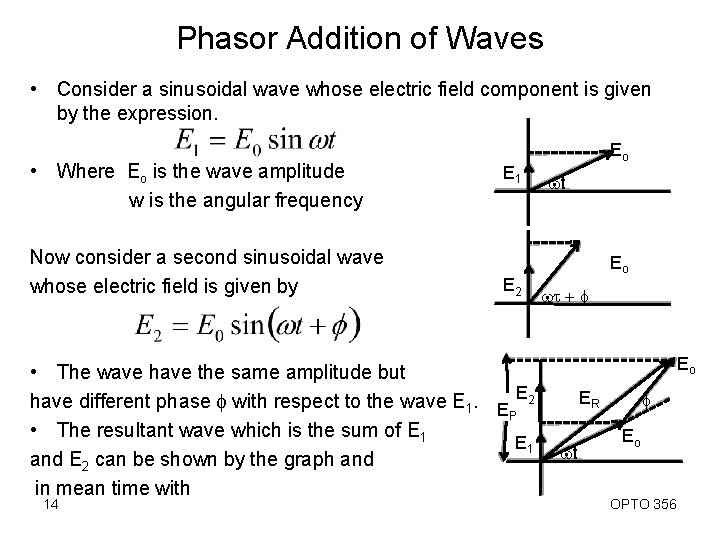
Phasor Addition of Waves • Consider a sinusoidal wave whose electric field component is given by the expression. • Where Eo is the wave amplitude w is the angular frequency Now consider a second sinusoidal wave whose electric field is given by E 1 E 2 • The wave have the same amplitude but have different phase f with respect to the wave E 1. E E 2 P • The resultant wave which is the sum of E 1 and E 2 can be shown by the graph and in mean time with 14 Eo wt + f Eo ER wt f Eo OPTO 356

Where sin A + sin B = 2 sin [(A+B)/2] So the final total electric field will be cos [(A-B)/2] The light intensity of light will be Since most light detecting instruments measure the time average light intensity and the time average value of over one cycle is ½ we can write the average intensity as Where Io is the maximum possible intensity but in your mind that From the last two equations We can determine the intensity as 15 OPTO 356

• Alternatively, since sin q = y /L for small values of q, we can write the intensity equation in the form • • Constrictive interference which produce intensity maxima, occurs when the quantity (pyd/l. L) is an integral multiple of p, corresponding to y = (l. L /d)m 16 OPTO 356

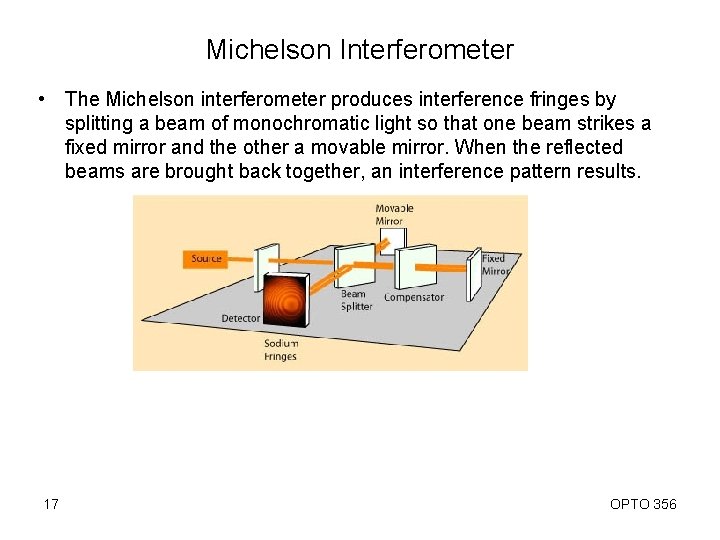
Michelson Interferometer • The Michelson interferometer produces interference fringes by splitting a beam of monochromatic light so that one beam strikes a fixed mirror and the other a movable mirror. When the reflected beams are brought back together, an interference pattern results. 17 OPTO 356

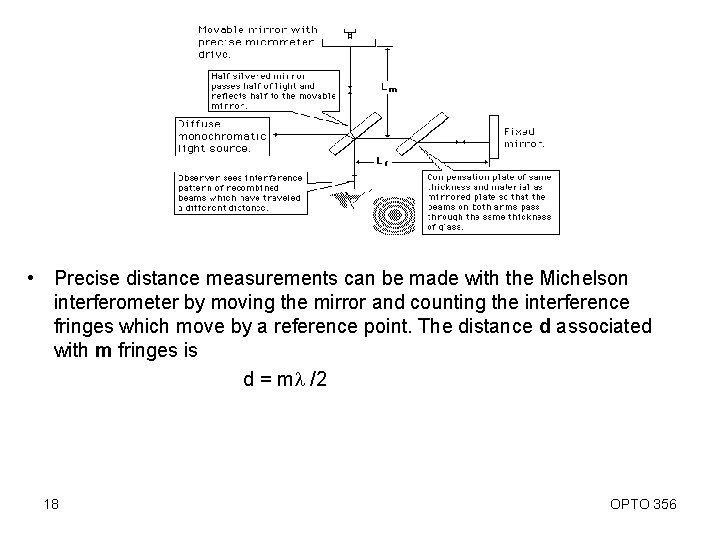
• Precise distance measurements can be made with the Michelson interferometer by moving the mirror and counting the interference fringes which move by a reference point. The distance d associated with m fringes is d = ml /2 18 OPTO 356