Diffraction Elliott Basics If we pass waves through

Diffraction Elliott

Basics If we pass waves through a single slit, we observe that the waves spread out due to diffraction. • If the slit is narrow, the diffraction is more marked. • The wavelength remains the same. • Diffraction does not need a slit. Waves can bend round a barrier by diffraction. Radio signals can be picked up behind hills for this reason. • The longer the wavelength, the more the waves will diffract. • All waves diffract.

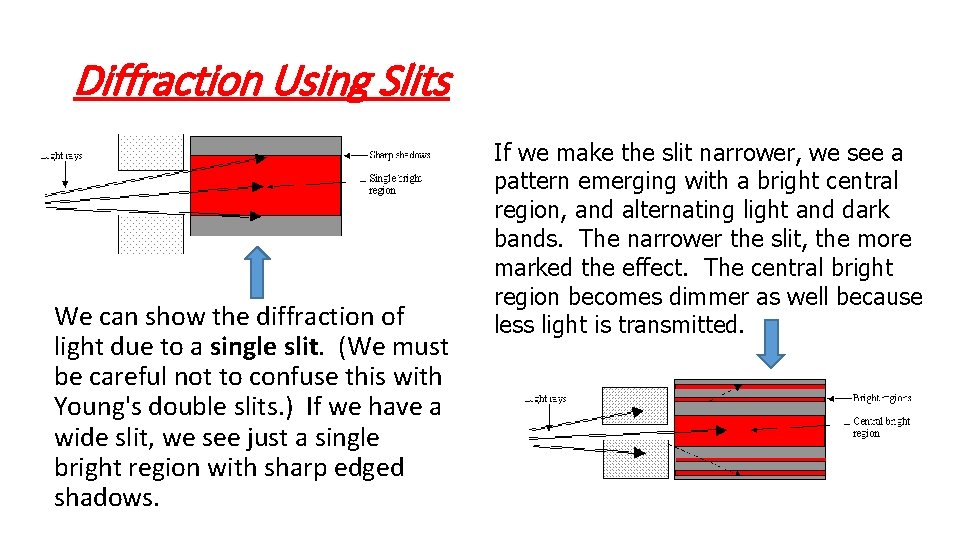
Diffraction Using Slits We can show the diffraction of light due to a single slit. (We must be careful not to confuse this with Young's double slits. ) If we have a wide slit, we see just a single bright region with sharp edged shadows. If we make the slit narrower, we see a pattern emerging with a bright central region, and alternating light and dark bands. The narrower the slit, the more marked the effect. The central bright region becomes dimmer as well because less light is transmitted.

Monochromatic Light Vs White light • If the light is monochromatic, the bands will be of the same colour. • Red light has a broader pattern than blue light, suggesting that the diffraction effect increases with wave length. If we use white light, the central band is white, with the fringes being overlapped with the spectrum of colours. This is called Fraunhoffer diffraction.

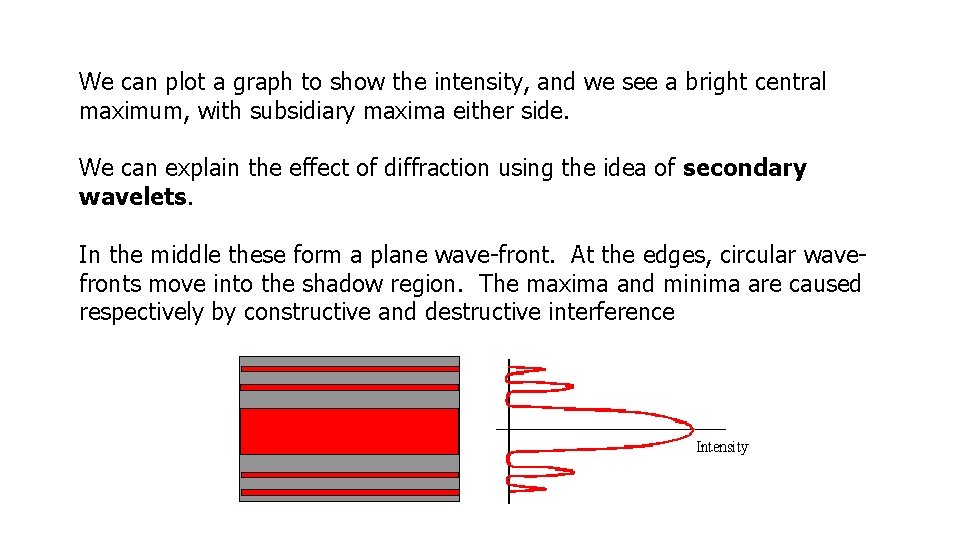
We can plot a graph to show the intensity, and we see a bright central maximum, with subsidiary maxima either side. We can explain the effect of diffraction using the idea of secondary wavelets. In the middle these form a plane wave-front. At the edges, circular wavefronts move into the shadow region. The maxima and minima are caused respectively by constructive and destructive interference

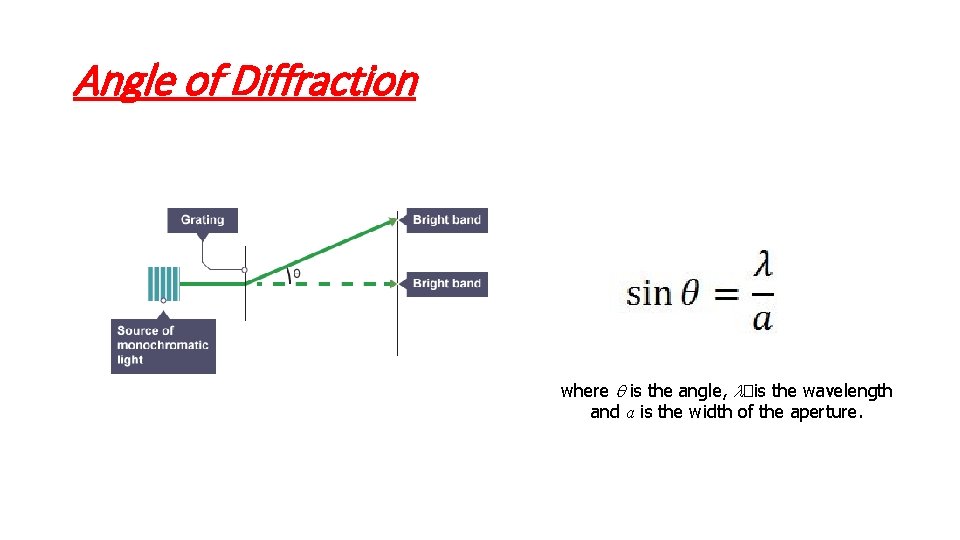
Angle of Diffraction where q is the angle, l�is the wavelength and a is the width of the aperture.

Worked Example A piano note of 256 Hz is played. It is heard through a door 200 cm wide. What is the maximum angle of diffraction that will occur if the speed of sound in air is 336 m/s? Answer We need to know the wavelength at first: l�= c/f Þ�l�= 336 m s-1 = 1. 31 m 256 Hz Now we can work out q: sin q = l�= 1. 31 m a 2. 0 m Þ sin q = 0. 655 Þ�q = 41 o If the door were less than 1. 31 m wide, diffraction could not occur because sin q would be greater than 1, which is impossible.

Check Your Progress The ASTRA satellite transmits radio waves (speed = 3 ´ 108 m/s) at a frequency of 12. 5 GHz. (1 GHz = 1 ´ 109 Hz) (a) What is the wavelength of the signal? (b) The transmitting dish is 1. 6 m in diameter. Find the angle of diffraction. (c) What is the radius of the circular patch that receives the signal? The height of the satellite is 3. 6 ´ 107 m above the earth. (Ignore the curvature of the Earth)

Answer (a) l = c/f = 3 ´ 108 m s-1 ¸� 12. 5 ´� 109 Hz = 0. 024 m (= 2. 4 cm) (b) sin q = l/a = 0. 024 m ÷ 1. 6 m = 0. 015 q = sin-1 0. 015 = 0. 86 o (c) Radius = 3. 6 ´ 107 m ´ tan 0. 86 = 3. 6 ´ 107 m ´� 0. 015 = 540 000 m (= 540 km)

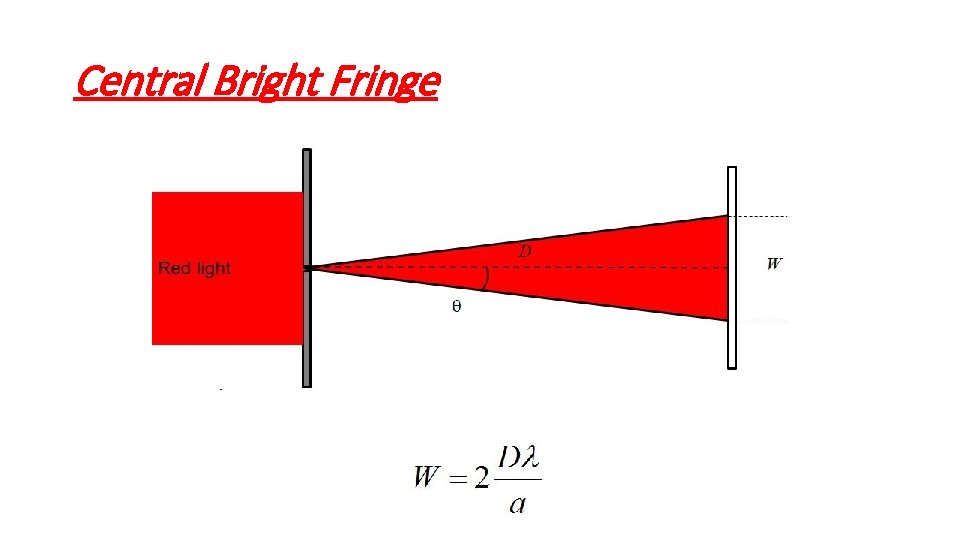
Central Bright Fringe

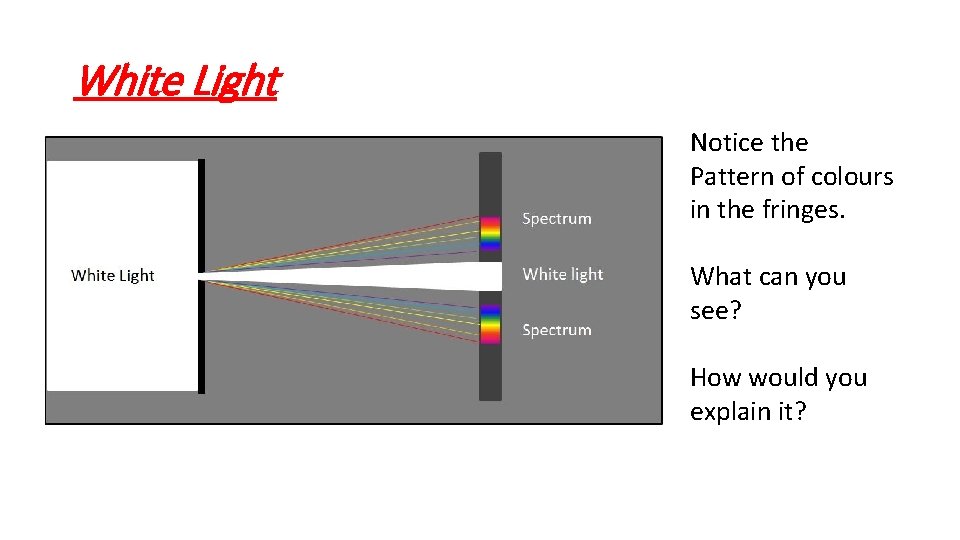
White Light Notice the Pattern of colours in the fringes. What can you see? How would you explain it?