Diffraction Analysis of crystal structure xrays neutrons and

Diffraction Analysis of crystal structure x-rays, neutrons and electrons 2/2 -10 MENA 3100

The reciprocal lattice • g is a vector normal to a set of planes, with length equal to the inverse spacing between them • Reciprocal lattice vectors a*, b* and c* • These vectors define the reciprocal lattice • All crystals have a real space lattice and a reciprocal lattice • Diffraction techniques map the reciprocal lattice 2/2 -10 MENA 3100

Radiation: x-rays, neutrons and electrons • Elastic scattering of radiation – No energy is lost • The wave length of the scattered wave remains unchanged • Regular arrays of atoms interact elastically with radiation of sufficient short wavelength – Cu. Kα x-ray radiation: λ=0. 154 nm • Scattered by electrons • ~from sub mm regions – Neutron radiation λ~0. 1 nm • Scattered by atomic nuclei • Several cm thick samples – Electron radiation (200 k. V): λ=0. 00251 nm • Scattered by atomic nuclei and electrons • Thickness less than ~200 nm 2/2 -10 MENA 3100

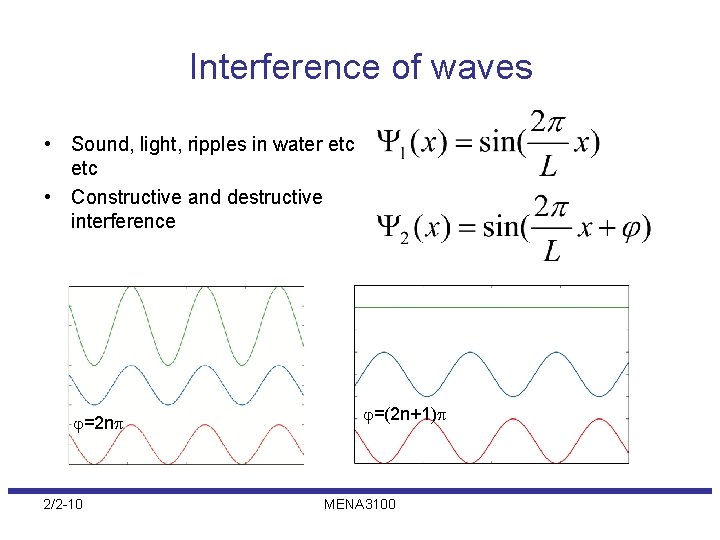
Interference of waves • Sound, light, ripples in water etc • Constructive and destructive interference =2 n 2/2 -10 =(2 n+1) MENA 3100

Nature of light • Newton: particles (corpuscles) • Huygens: waves • Thomas Young double slit experiment (1801) • Path difference phase difference • Light consists of waves ! • Wave-particle duality 2/2 -10 MENA 3100

Discovery of X-rays • • • Wilhelm Röntgen 1895/96 Nobel Prize in 1901 Particles or waves? Not affected by magnetic fields No refraction, reflection or intereference observed • If waves, λ 10 -9 m 2/2 -10 MENA 3100

Max von Laue • • • The periodicity and interatomic spacing of crystals had been deduced earlier (e. g. Auguste Bravais). von Laue realized that if X-rays were waves with short wavelength, interference phenomena should be observed like in Young’s double slit experiment. Experiment in 1912, Nobel Prize in 1914 2/2 -10 MENA 3100

Laue conditions Scattering from a periodic distribution of scatters along the a axis ko a k The scattered wave will be in phase and constructive interference will occur if the phase difference is 2π. Φ=2πa. (k-ko)=2πa. g= 2πh, similar for b and c 2/2 -10 MENA 3100

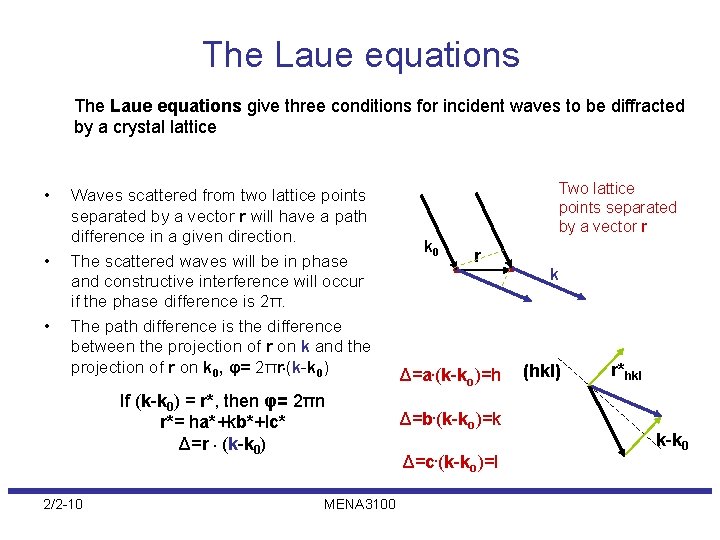
The Laue equations give three conditions for incident waves to be diffracted by a crystal lattice • • • Waves scattered from two lattice points separated by a vector r will have a path difference in a given direction. The scattered waves will be in phase and constructive interference will occur if the phase difference is 2π. The path difference is the difference between the projection of r on k and the projection of r on k 0, φ= 2πr. (k-k 0) If (k-k 0) = r*, then φ= 2πn r*= ha*+kb*+lc* Δ=r. (k-k 0) 2/2 -10 MENA 3100 Two lattice points separated by a vector r k 0 r Δ=a. (k-ko)=h Δ=b. (k-ko)=k Δ=c. (k-ko)=l k (hkl) r*hkl k-k 0

Bragg’s law • William Henry and William Lawrence Bragg (father and son) found a simple interpretation of von Laue’s experiment • Consider a crystal as a periodic arrangement of atoms, this gives crystal planes • Assume that each crystal plane reflects radiation as a mirror • Analyze this situation for cases of constructive and destructive interference • Nobel prize in 1915 2/2 -10 MENA 3100

Derivation of Bragg’s law θ dhkl x Path difference Δ= 2 x => phase shift Constructive interference if Δ=nλ This gives the criterion for constructive interference: Bragg’s law tells you at which angle θB to expect maximum diffracted intensity for a particular family of crystal planes. For large crystals, all other angles give zero intensity. 2/2 -10 MENA 3100

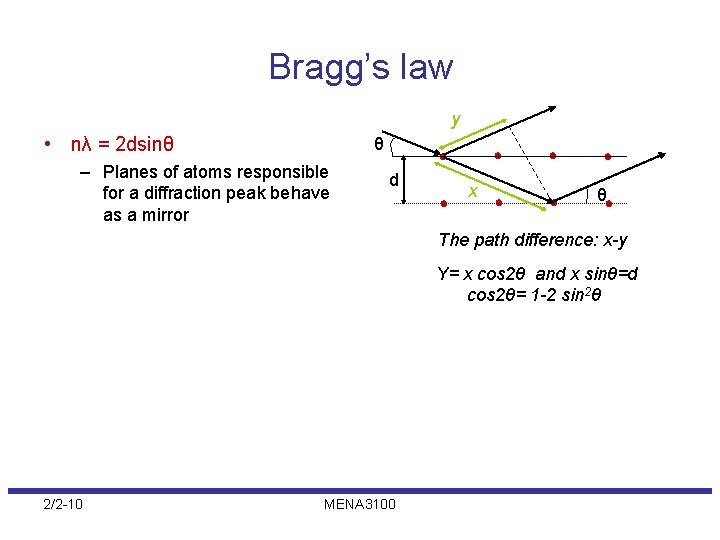
Bragg’s law y • nλ = 2 dsinθ θ – Planes of atoms responsible for a diffraction peak behave as a mirror d x θ The path difference: x-y Y= x cos 2θ and x sinθ=d cos 2θ= 1 -2 sin 2θ 2/2 -10 MENA 3100

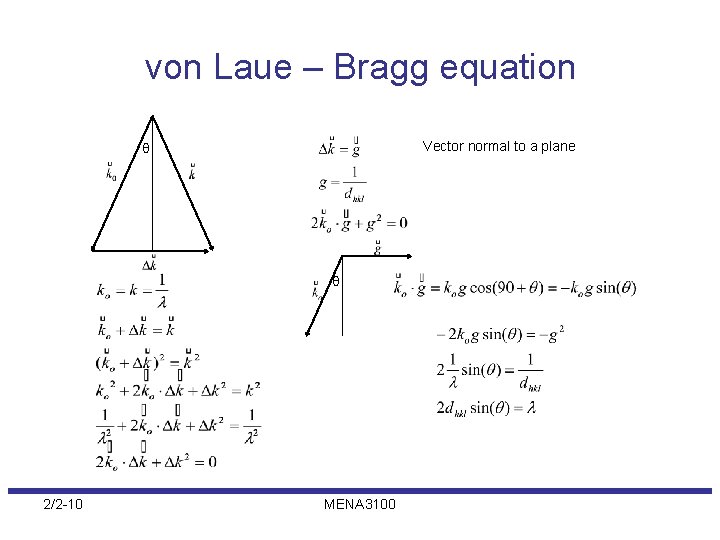
von Laue – Bragg equation Vector normal to a plane θ θ 2/2 -10 MENA 3100

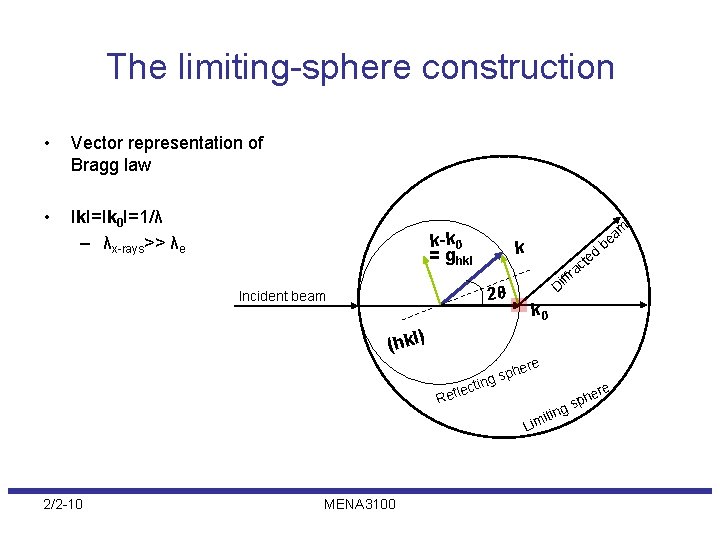
The limiting-sphere construction • Vector representation of Bragg law • Ik. I=Ik 0 I=1/λ – λx-rays>> λe k-k 0 = ghkl k r 2θ ff Di Incident beam ed t ac am e b k 0 (hkl) cti le Ref ere ph ng s re it Lim 2/2 -10 MENA 3100 ing e sph

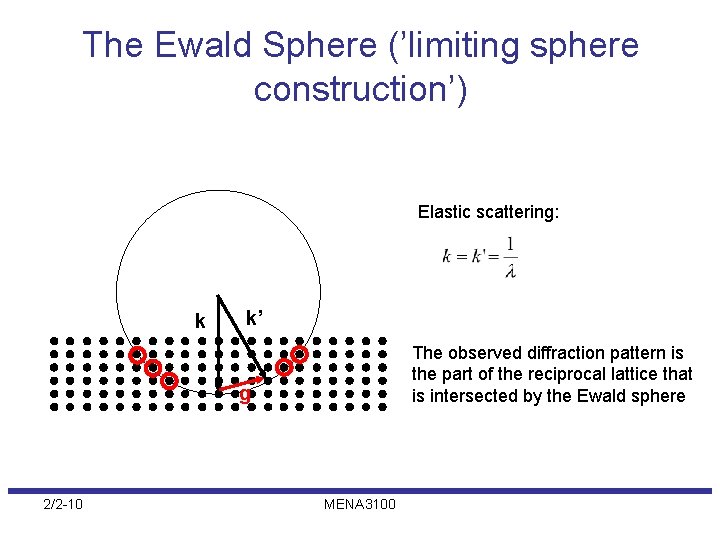
The Ewald Sphere (’limiting sphere construction’) Elastic scattering: k k’ The observed diffraction pattern is the part of the reciprocal lattice that is intersected by the Ewald sphere g 2/2 -10 MENA 3100

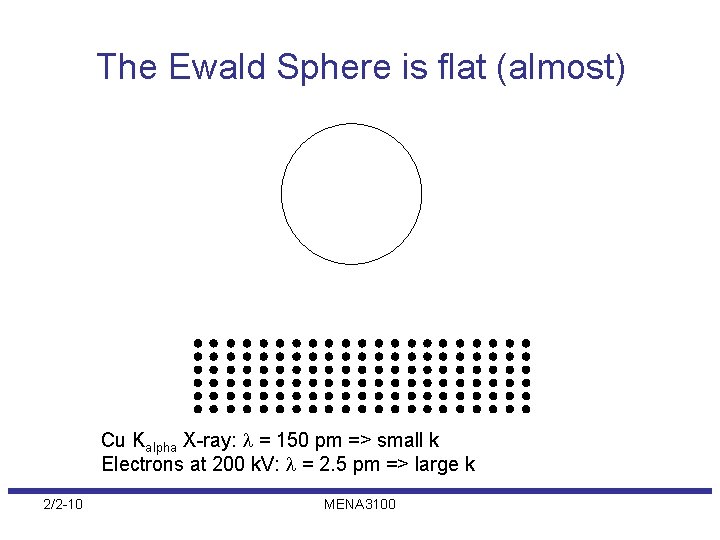
The Ewald Sphere is flat (almost) Cu Kalpha X-ray: = 150 pm => small k Electrons at 200 k. V: = 2. 5 pm => large k 2/2 -10 MENA 3100

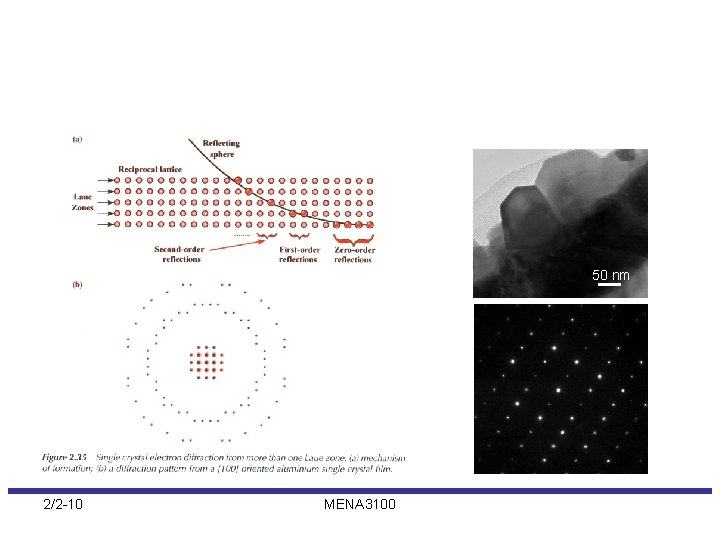
50 nm 2/2 -10 MENA 3100

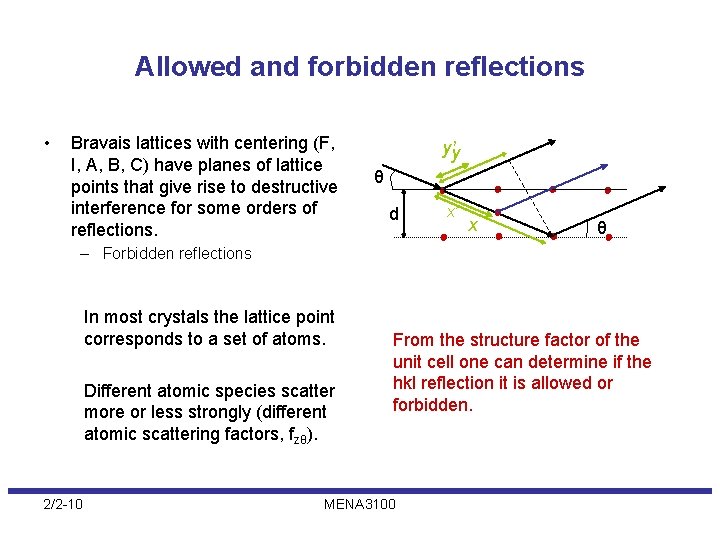
Allowed and forbidden reflections • Bravais lattices with centering (F, I, A, B, C) have planes of lattice points that give rise to destructive interference for some orders of reflections. y’y θ d x’ x θ – Forbidden reflections In most crystals the lattice point corresponds to a set of atoms. Different atomic species scatter more or less strongly (different atomic scattering factors, fzθ). 2/2 -10 From the structure factor of the unit cell one can determine if the hkl reflection it is allowed or forbidden. MENA 3100

Structure factors X-ray: The coordinate of atom j within the crystal unit cell is given rj=uja+vjb+wjc. h, k and l are the miller indices of the Bragg reflection g. N is the number of atoms within the crystal unit cell. fj(n) is the x-ray scattering factor, or x-ray scattering amplitude, for atom j. wj c The structure factors for x-ray, neutron and electron diffraction are similar. For neutrons and electrons we need only to replace by fj(n) or fj(e). z rj c a b vjb uj a y x 2/2 -10 The intensity of a reflection is proportional to: MENA 3100

Example: fcc • • • eiφ = cosφ + isinφ enπi = (-1)n eix + e-ix = 2 cosx Atomic positions in the unit cell: [000], [½ ½ 0], [½ 0 ½ ], [0 ½ ½ ] What is the general condition for reflections for fcc? What is the general condition for reflections for bcc? Fhkl= f (1+ eπi(h+k) + eπi(h+l) + eπi(k+l)) If h, k, l are all odd then: Fhkl= f(1+1+1+1)=4 f If h, k, l are mixed integers (exs 112) then Fhkl=f(1+1 -1 -1)=0 (forbidden) 2/2 -10 MENA 3100

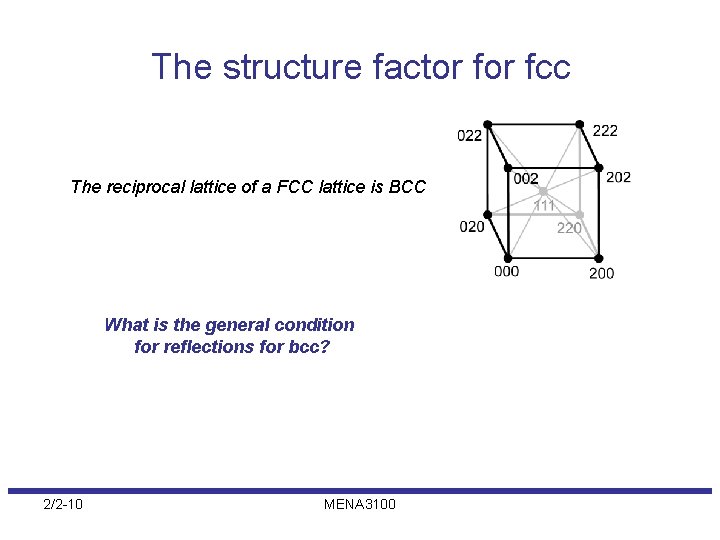
The structure factor fcc The reciprocal lattice of a FCC lattice is BCC What is the general condition for reflections for bcc? 2/2 -10 MENA 3100

The reciprocal lattice of bcc • Body centered cubic lattice • One atom per lattice point, [000] relative to the lattice point • What is the reciprocal lattice? 2/2 -10 MENA 3100