Diffraction Analysis of crystal structure xrays neutrons and

Diffraction Analysis of crystal structure x-rays, neutrons and electrons 29/1 -08 MENA 3100

Radiation: x-rays, neutrons and electrons • Elastic scattering of radiation – No energy is lost • The wave length of the scattered wave remains unchanged • Regular arrays of atoms interact elastically with radiation of sufficient short wavelength – Cu. Kα x-ray radiation: λ=0. 154 nm • Scattered by electrons • ~from sub mm regions – Electron radiation (200 k. V): λ=0. 00251 nm • Scattered by atomic nuclei and electrons • Thickness less than ~200 nm – Neutron radiation λ~0. 1 nm • Scattered by atomic nuclei • Several cm thick samples 29/1 -08 MENA 3100

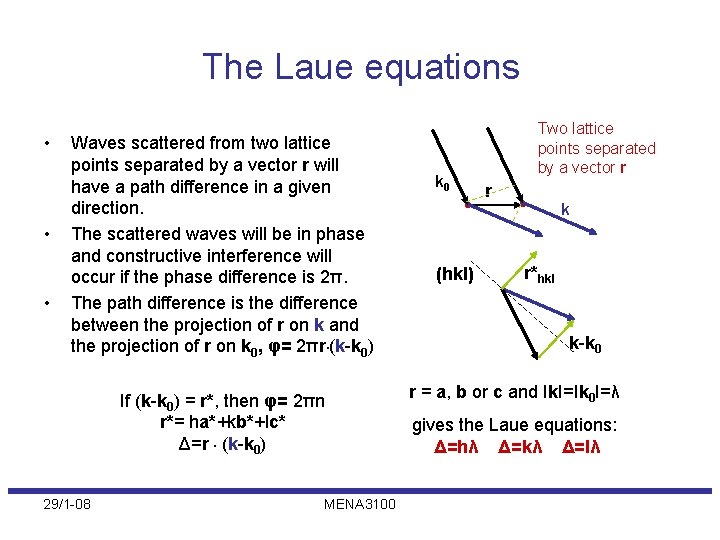
The Laue equations • • • Waves scattered from two lattice points separated by a vector r will have a path difference in a given direction. The scattered waves will be in phase and constructive interference will occur if the phase difference is 2π. The path difference is the difference between the projection of r on k and the projection of r on k 0, φ= 2πr. (k-k 0) If (k-k 0) = r*, then φ= 2πn r*= ha*+kb*+lc* Δ=r. (k-k 0) 29/1 -08 MENA 3100 k 0 (hkl) Two lattice points separated by a vector r r k r*hkl k-k 0 r = a, b or c and Ik. I=Ik 0 I=λ gives the Laue equations: Δ=hλ Δ=kλ Δ=lλ

Bragg’s law y • nλ = 2 dsinθ θ – Planes of atoms responsible for a diffraction peak behave as a mirror d x θ The path difference: x-y • 1/d 2=(h/a)2+(k/b)2+(l/c)2 Y= x cos 2θ and x sinθ=d cos 2θ= 1 -2 sin 2θ – Orthorhombic lattice (hkl) ghkl = r*hkl 29/1 -08 MENA 3100 r*hkl k-k 0

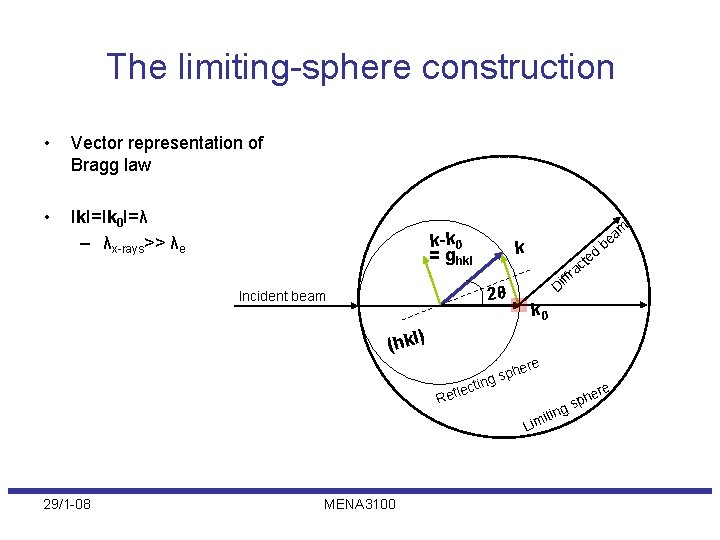
The limiting-sphere construction • Vector representation of Bragg law • Ik. I=Ik 0 I=λ – λx-rays>> λe k-k 0 = ghkl k r 2θ ff Di Incident beam ed t ac am e b k 0 (hkl) cti le Ref ere ph ng s re it Lim 29/1 -08 MENA 3100 ing e sph

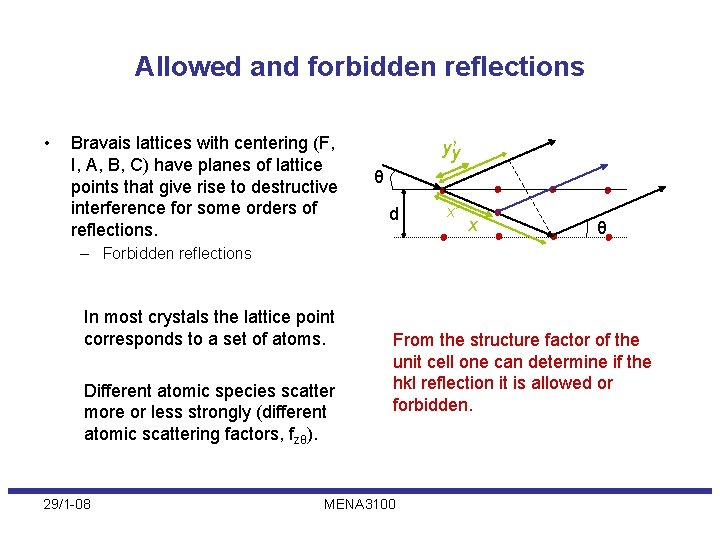
Allowed and forbidden reflections • Bravais lattices with centering (F, I, A, B, C) have planes of lattice points that give rise to destructive interference for some orders of reflections. y’y θ d x’ x θ – Forbidden reflections In most crystals the lattice point corresponds to a set of atoms. Different atomic species scatter more or less strongly (different atomic scattering factors, fzθ). 29/1 -08 From the structure factor of the unit cell one can determine if the hkl reflection it is allowed or forbidden. MENA 3100

Structure factors X-ray: The coordinate of atom j within the crystal unit cell is given rj=uja+vjb+wjc. h, k and l are the miller indices of the Bragg reflection g. N is the number of atoms within the crystal unit cell. fj(n) is the x-ray scattering factor, or x-ray scattering amplitude, for atom j. wj c The structure factors for x-ray, neutron and electron diffraction are similar. For neutrons and electrons we need only to replace by fj(n) or fj(e). z rj c a b vjb uj a y x 29/1 -08 The intensity of a reflection is proportional to: MENA 3100

Example: Cu, fcc • • • eiφ = cosφ + isinφ enπi = (-1)n eix + e-ix = 2 cosx Atomic positions in the unit cell: [000], [½ ½ 0], [½ 0 ½ ], [0 ½ ½ ] Fhkl= f (1+ eπi(h+k) + eπi(h+l) + eπi(k+l)) What is the general condition for reflections for fcc? What is the general condition for reflections for bcc? 29/1 -08 If h, k, l are all odd then: Fhkl= f(1+1+1+1)=4 f If h, k, l are mixed integers (exs 112) then Fhkl=f(1+1 -1 -1)=0 (forbidden) MENA 3100