Difflog Beyond Deductive Methods in Program Analysis Mukund

Difflog: Beyond Deductive Methods in Program Analysis Mukund Raghothaman · Sulekha Kulkarni · Richard Zhang Xujie Si · Kihong Heo · Woosuk Lee · Mayur Naik University of Pennsylvania

Static Analyzers • Automatic bug-finding tools • The ideal static analyzer: Astrée Microsoft Windows Device Drivers Airbus Avionics Software Synopsis Enterprise Applications Facebook Mobile Applications • Identifies the most serious bugs • Produces no false alarms • Scales to very large codebases MLP 2018 Beyond Deductive Methods in Program Analysis 2

• Heartbleed • Buffer over‑read bug in Open. SSL’s implementation Why. Heartbeat did static analysis tools not • Introduced in 2011, discovered in 2014 discover theto. Heartbleed bug? • Estimated affect nearly 66% of all web servers MLP 2018 Beyond Deductive Methods in Program Analysis 3

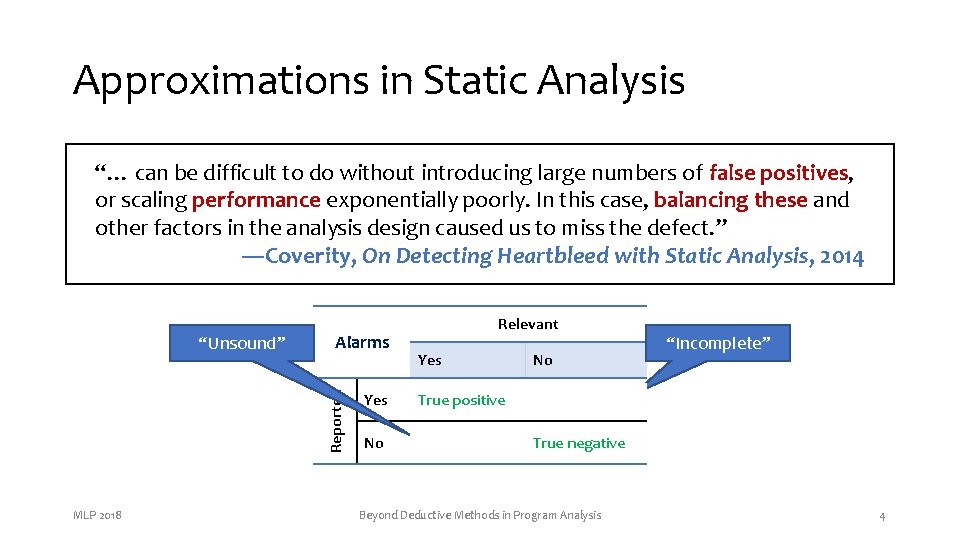
Approximations in Static Analysis • Challenge #1: Most analysis are undecidable “… can be difficult to do without questions introducing large numbers of false positives, So, analysis tools areexponentially only approximately correct or scaling performance poorly. In this case, balancing these and other factors#2: in the analysis design caused us toprograms miss the defect. ” • Challenge Tools must scale to large ―Coverity, make On Detecting Heartbleed with Static Analysis, 2014 So, analysis designers aggressive tradeoffs Alarms Reported “Unsound” MLP 2018 Relevant Yes No Yes True positive False positive No False negative True negative Beyond Deductive Methods in Program Analysis “Incomplete” 4

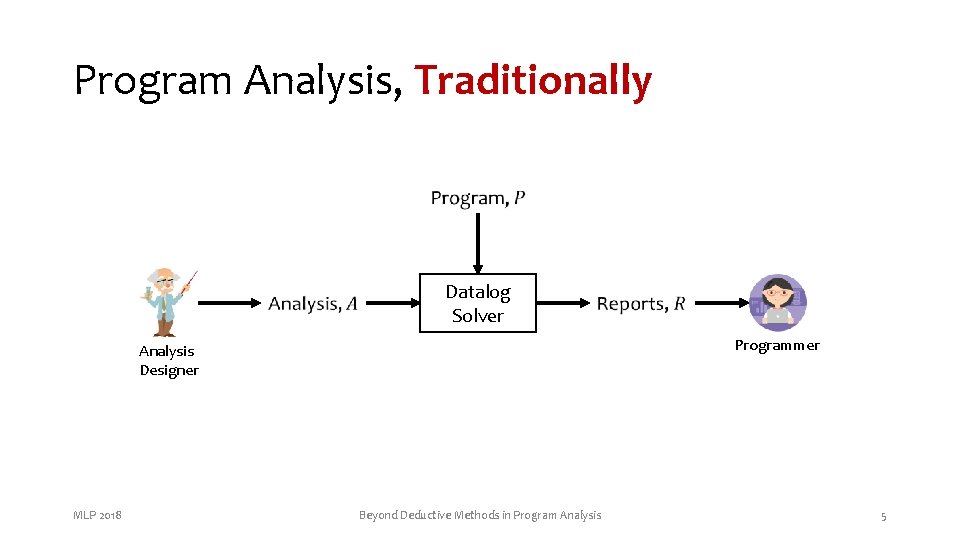
Program Analysis, Traditionally Datalog Solver Programmer Analysis Designer MLP 2018 Beyond Deductive Methods in Program Analysis 5

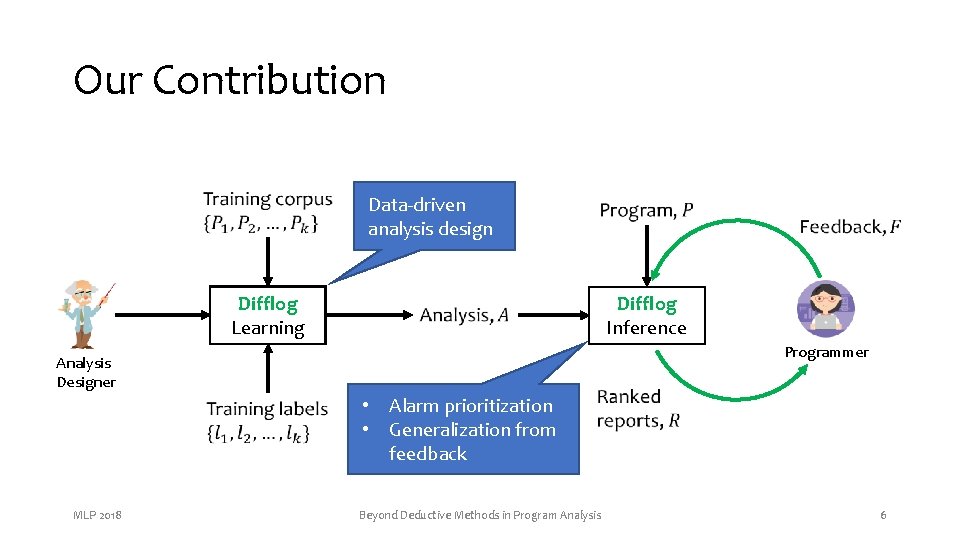
Our Contribution Data-driven analysis design Difflog Learning Difflog Inference Programmer Analysis Designer • Alarm prioritization • Generalization from feedback MLP 2018 Beyond Deductive Methods in Program Analysis 6

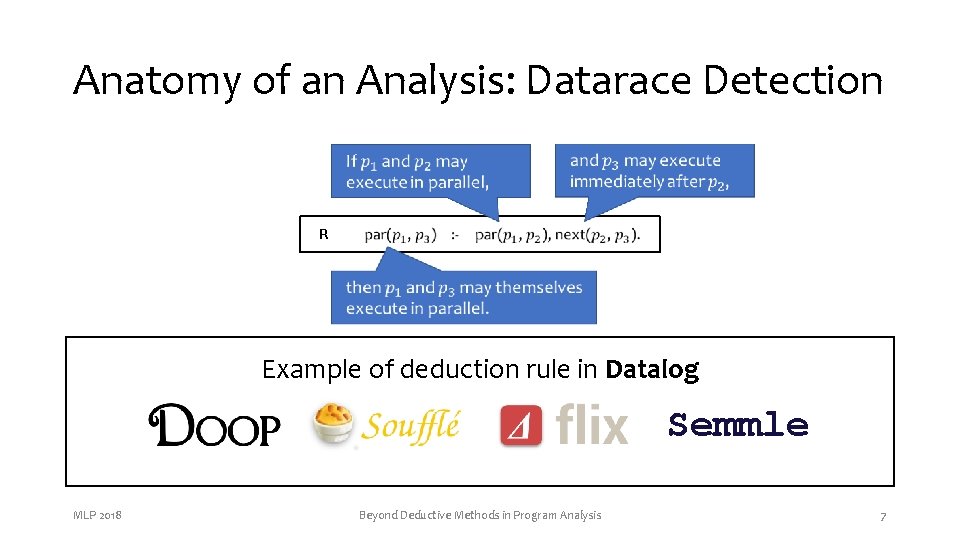
Anatomy of an Analysis: Datarace Detection R , L 2) next(L 2, L 3) Example of deduction rulepar(L in 1 Datalog ⋮ x = y + 1; // L 1 ⋮ MLP 2018 ⋮ z = y + 1; // L 2 z = z + 1; // L 3 ⋮ Beyond Deductive Methods in Program Analysis Semmle R par(L 1, L 3) 7

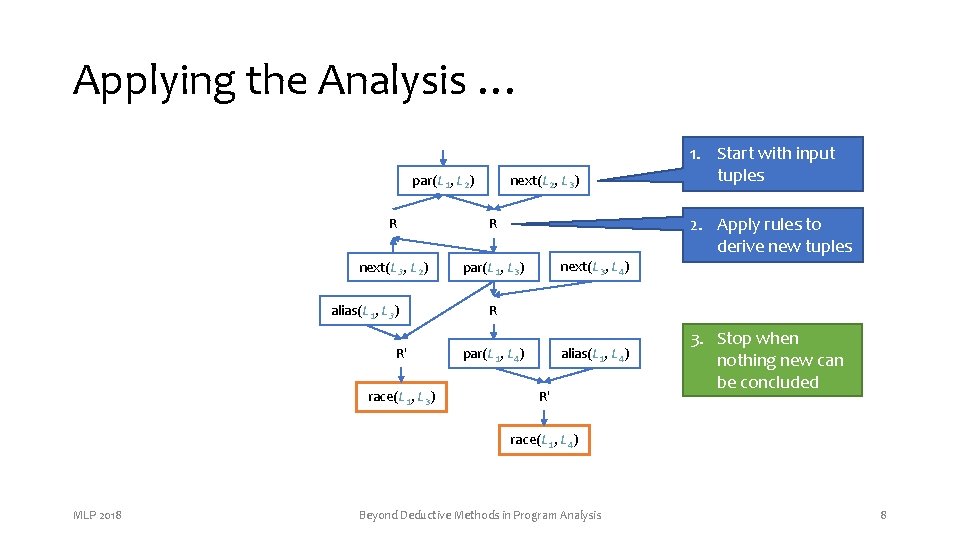
Applying the Analysis … par(L 1, L 2) next(L 2, L 3) 2. Apply rules to derive new tuples R R next(L 3, L 2) par(L 1, L 3) alias(L 1, L 3) R′ race(L 1, L 3) 1. Start with input tuples next(L 3, L 4) R alias(L 1, L 4) par(L 1, L 4) R′ 3. Stop when nothing new can be concluded race(L 1, L 4) MLP 2018 Beyond Deductive Methods in Program Analysis 8

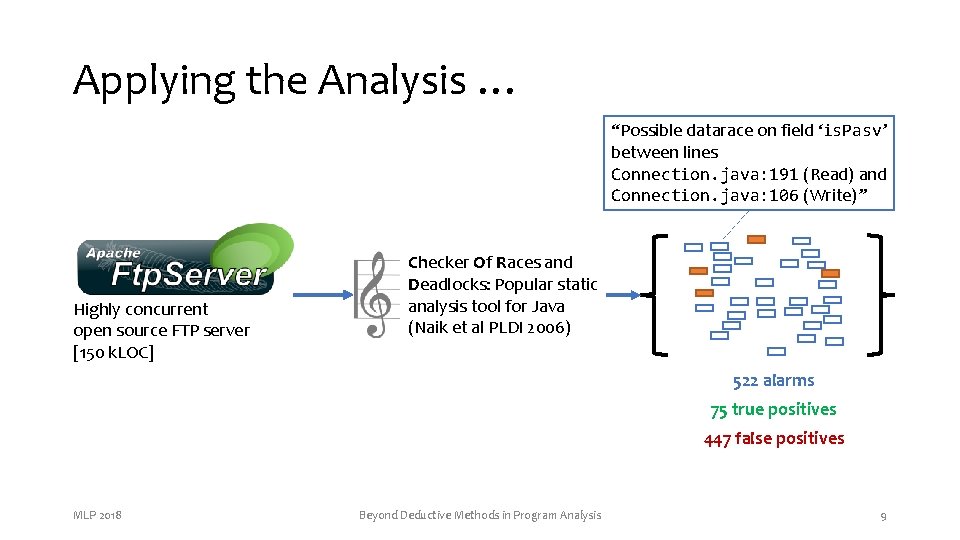
Applying the Analysis … “Possible datarace on field ‘is. Pasv’ between lines Connection. java: 191 (Read) and Connection. java: 106 (Write)” Highly concurrent open source FTP server [150 k. LOC] Checker Of Races and Deadlocks: Popular static analysis tool for Java (Naik et al PLDI 2006) 522 alarms 75 true positives 447 false positives MLP 2018 Beyond Deductive Methods in Program Analysis 9

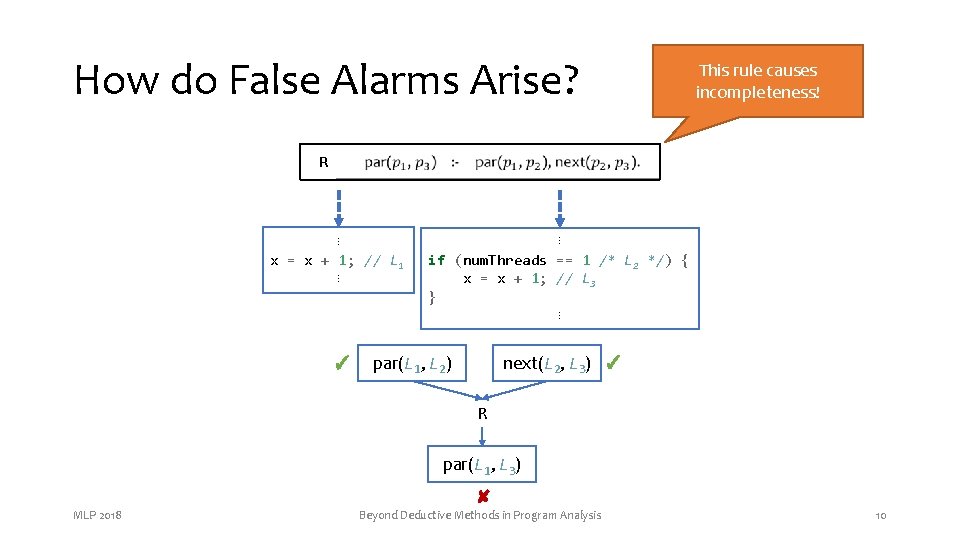
How do False Alarms Arise? This rule causes incompleteness! R ⋮ x = x + 1; // L 1 ⋮ ✓ ⋮ if (num. Threads == 1 /* L 2 */) { x = x + 1; // L 3 } ⋮ par(L 1, L 2) next(L 2, L 3) ✓ R par(L 1, L 3) ✘ MLP 2018 Beyond Deductive Methods in Program Analysis 10

How do False Alarms Arise? • Incorrect intermediate conclusions lead to false alarms downstream • Traditional solution: • • MLP 2018 Refine the analysis, use more elaborate rules Requires domain expertise Makes analysis computationally expensive Effectiveness depends on program and on coding idioms Beyond Deductive Methods in Program Analysis 11

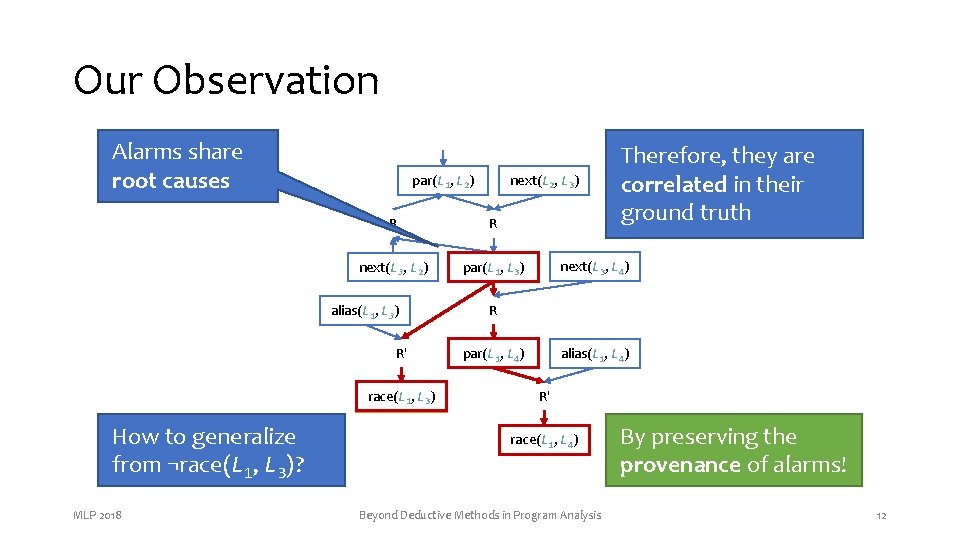
Our Observation Alarms share root causes par(L 1, L 2) R R next(L 3, L 2) par(L 1, L 3) alias(L 1, L 3) R′ race(L 1, L 3) How to generalize from ¬race(L 1, L 3)? MLP 2018 next(L 2, L 3) Therefore, they are correlated in their ground truth next(L 3, L 4) R par(L 1, L 4) alias(L 1, L 4) R′ race(L 1, L 4) Beyond Deductive Methods in Program Analysis By preserving the provenance of alarms! 12

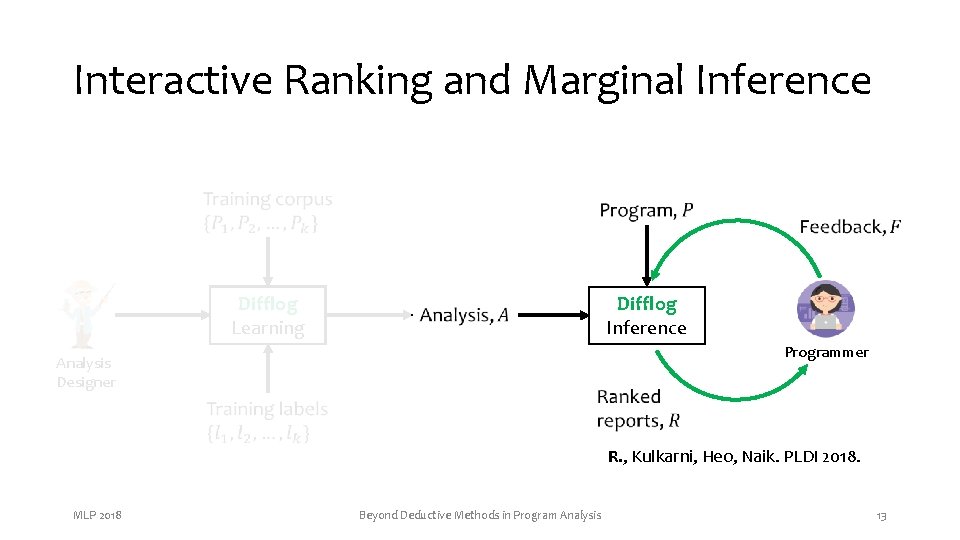
Interactive Ranking and Marginal Inference Difflog Learning Difflog Inference Programmer Analysis Designer R. , Kulkarni, Heo, Naik. PLDI 2018. MLP 2018 Beyond Deductive Methods in Program Analysis 13

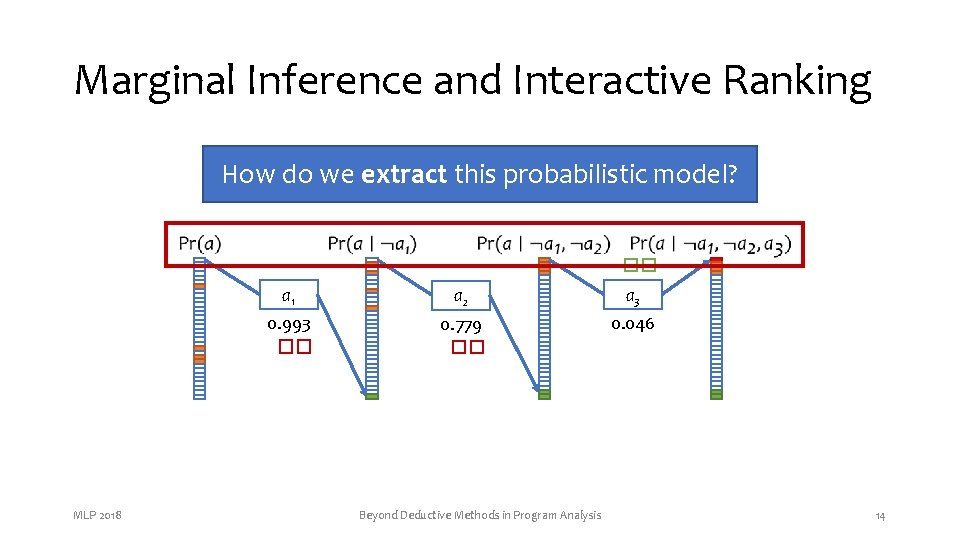
Marginal Inference and Interactive Ranking How do we extract this probabilistic model? �� MLP 2018 a 1 a 2 a 3 0. 993 �� 0. 779 �� 0. 046 Beyond Deductive Methods in Program Analysis 14

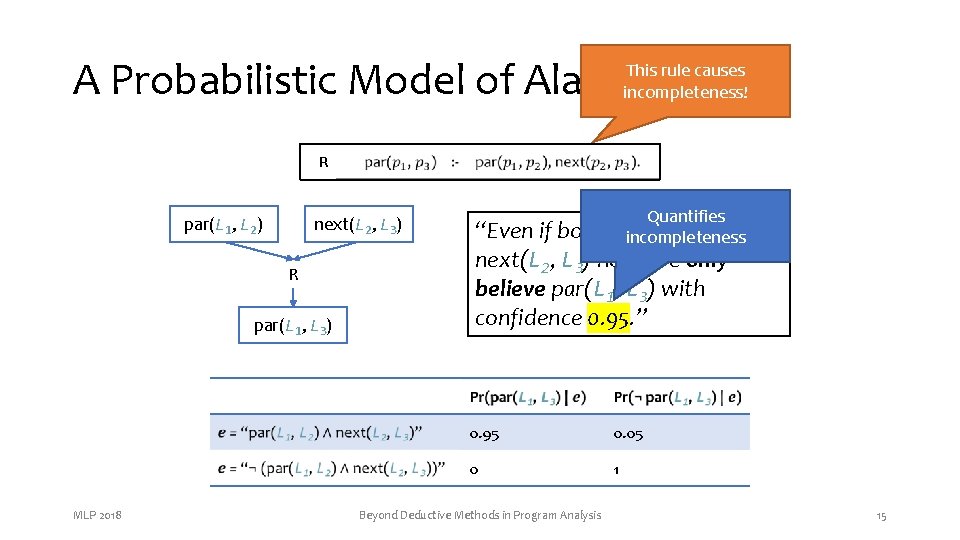
A Probabilistic Model of Alarms This rule causes incompleteness! R par(L 1, L 2) next(L 2, L 3) R par(L 1, L 3) MLP 2018 Quantifies “Even if both par(L L 22))and incompleteness 1, L next(L 2, LL 33))hold, we weonly believe par(L 1, LL 33))with confidence 0. 95. ” 0. 95 0. 05 0 1 Beyond Deductive Methods in Program Analysis 15

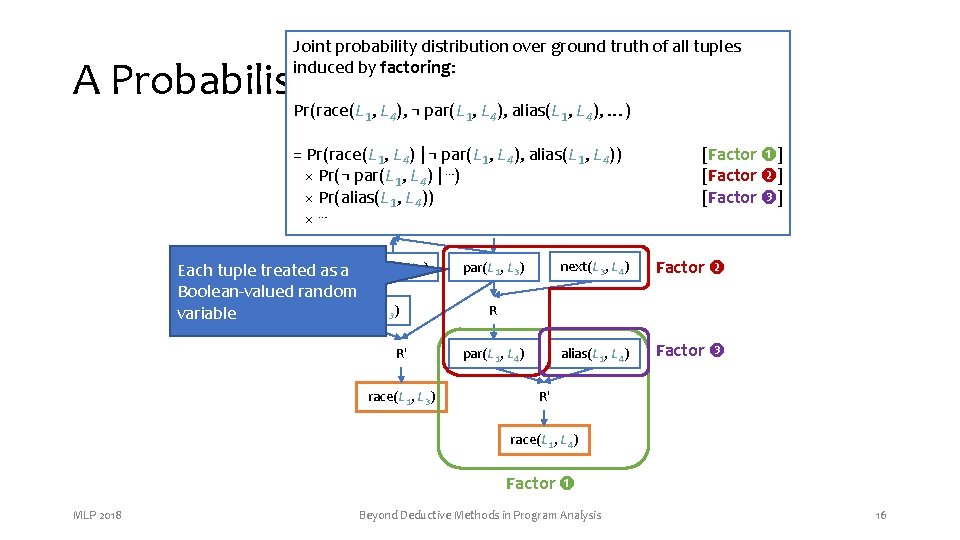
Joint probability distribution over ground truth of all tuples induced by factoring: A Probabilistic Model of Alarms Pr(race(L 1, L 4), ¬ par(L 1, L 4), alias(L 1, L 4), …) = Pr(race(L 1, L 4) | ¬ par(L 1, L 4), alias(L 1, L 4)) × Pr(¬ par(L 1, Lpar(L , L 2 ) next(L 2, L 3) 4) | 1⋯) × Pr(alias(L 1, L 4)) ×⋯ R R Each tuple treated as a next(L 3, L 2) Boolean-valued random alias(L 1, L 3) variable R′ race(L 1, L 3) par(L 1, L 3) [Factor ❶] [Factor ❷] [Factor ❸] next(L 3, L 4) Factor ❷ alias(L 1, L 4) Factor ❸ R par(L 1, L 4) R′ race(L 1, L 4) Factor ❶ MLP 2018 Beyond Deductive Methods in Program Analysis 16

Experimental Evaluation • Analysis 1: Datarace analysis for Java programs • Analysis 2: Taint analysis for Android apps • Suite of 16 benchmarks: Dacapo and Android malware • 40 K— 616 KLOC MLP 2018 Beyond Deductive Methods in Program Analysis 17

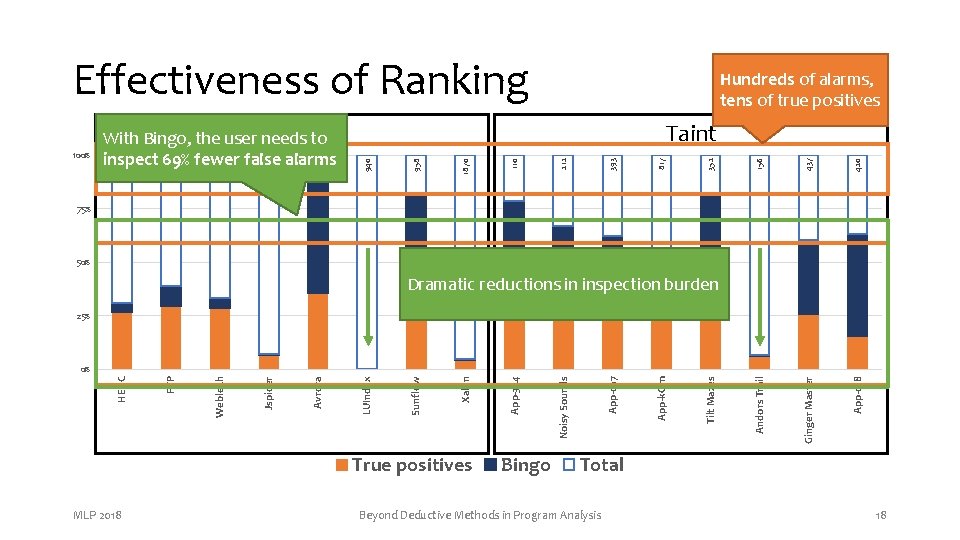
Effectiveness of Ranking 156 437 420 Andors Trail Ginger Master App-018 352 817 393 212 110 1870 958 Taint 940 978 257 30 522 152 100% Datarace With Bingo, the user needs to inspect 69% fewer false alarms Hundreds of alarms, tens of true positives 75% 50% Dramatic reductions in inspection burden 25% True positives MLP 2018 Bingo Tilt Mazes App-k. Qm App-ca 7 Noisy Sounds App-324 Xalan Sunflow LUIndex Avrora Jspider Weblech FTP HEDC 0% Total Beyond Deductive Methods in Program Analysis 18

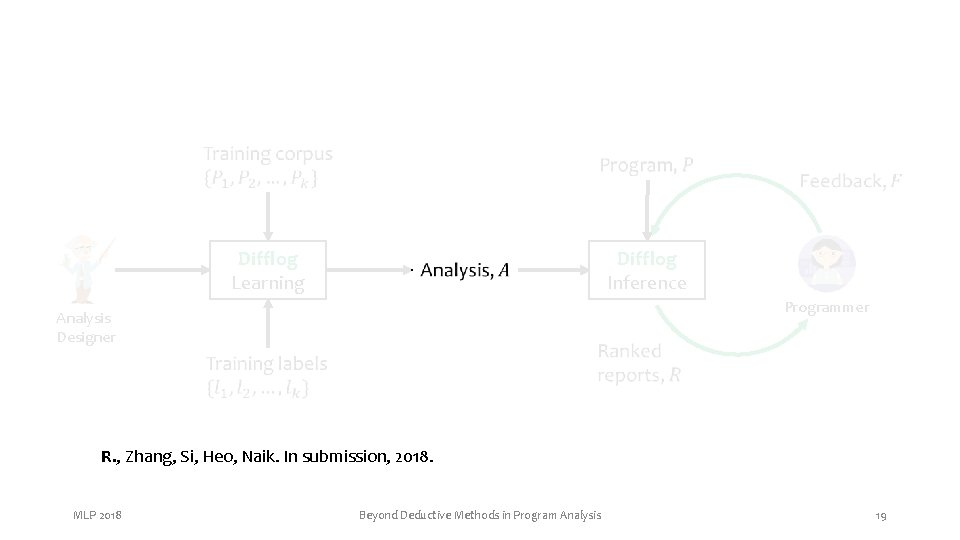
Difflog Learning Difflog Inference Programmer Analysis Designer R. , Zhang, Si, Heo, Naik. In submission, 2018. MLP 2018 Beyond Deductive Methods in Program Analysis 19

From the Discrete to the Continuous … Can we optimize for these values? MLP 2018 R 1 0. 90 R 2 0. 60 R 3 0. 80 R 4 0. 70 pt(b 1, c 1) pt(a, b 1) pt(b 1, c 2) pt(k, c 1) pt(k, c 2) 0. 90 0. 65 Beyond Deductive Methods in Program Analysis Rule weights induce numerical values for each conclusion Ideally, 1. 0 for true positives and 0. 0 for false alarms 20

From the Discrete to the Continuous … • Main challenge: Gradient descent would be very expensive • Because marginal inference is #P-complete • Because independence assumptions don’t always hold • Solution: Evaluate values using the Viterbi semiring instead MLP 2018 Beyond Deductive Methods in Program Analysis 21

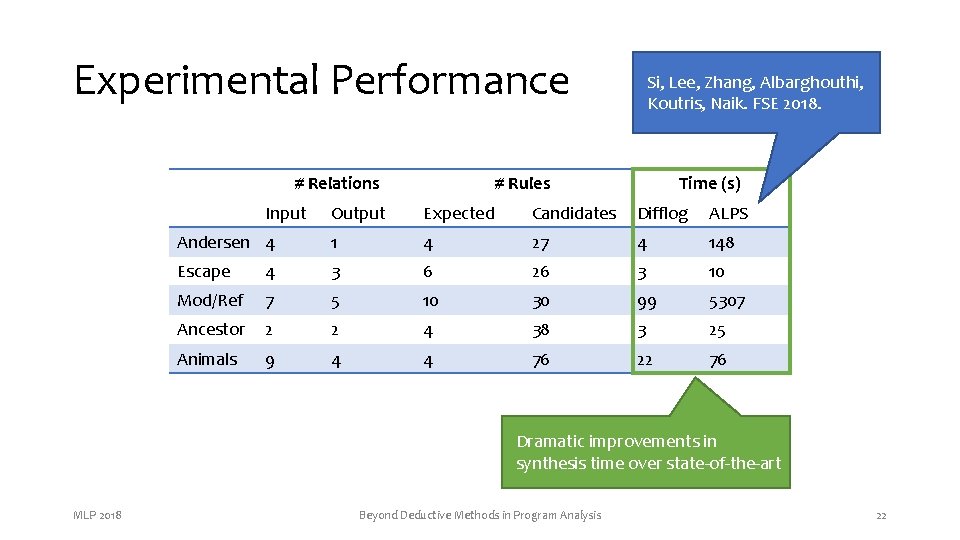
Experimental Performance # Relations Input Si, Lee, Zhang, Albarghouthi, Koutris, Naik. FSE 2018. # Rules Time (s) Output Expected Candidates Difflog ALPS Andersen 4 1 4 27 4 148 Escape 4 3 6 26 3 10 Mod/Ref 7 5 10 30 99 5307 Ancestor 2 2 4 38 3 25 Animals 9 4 4 76 22 76 Dramatic improvements in synthesis time over state-of-the-art MLP 2018 Beyond Deductive Methods in Program Analysis 22

Conclusion • Difflog: Framework to extend Datalog to continuous domains • Builds on theory of semiring provenance • Associates rules with tokens and computes provenance of alarms • Naturally captures alarm correlations • Enables data-driven analysis design • Interactive alarm prioritization MLP 2018 Beyond Deductive Methods in Program Analysis 23

Future Directions • Continuous integration and incremental analyses • Fault localization in complex systems • Combining numerical optimization and CDCL MLP 2018 Beyond Deductive Methods in Program Analysis 24