DifferentiationDiscrete Functions Mechanical Engineering Majors Authors Autar Kaw

Differentiation-Discrete Functions Mechanical Engineering Majors Authors: Autar Kaw, Sri Harsha Garapati http: //numericalmethods. eng. usf. edu Transforming Numerical Methods Education for STEM Undergraduates 11/9/2020 http: //numericalmethods. eng. usf. edu 1

Differentiation – Continuous. Discrete Functions http: //numericalmethods. eng. usf. edu

Forward Difference Approximation For a finite 3 lmethods. eng. usf. edu http: //numerica

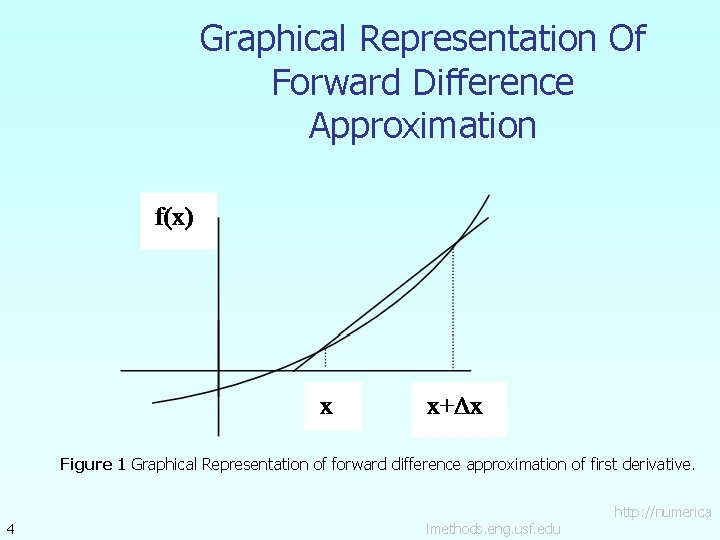
Graphical Representation Of Forward Difference Approximation Figure 1 Graphical Representation of forward difference approximation of first derivative. 4 lmethods. eng. usf. edu http: //numerica

Example 1 To find contraction of a steel cylinder immersed in a bath of liquid nitrogen, one needs to know thermal expansion coefficient data as a function of temperature. This data is given for steel in Table 1. a) Is the rate of change of coefficient of thermal expansion with respect to temperature more at than at ? b) The data given in Table 1 can be regressed to to get. . Compare the results with part (a) if you used the regression curve to find the rate of change of the coefficient of thermal expansion with respect to temperature at. and at. 5 lmethods. eng. usf. edu http: //numerica

Example 1 Cont. Table 1 Coefficient of thermal expansion as a function of temperature. Temperature, T (o. F) 6 Coefficient of thermal expansion, α (in/in/o. F) 80 6. 47 40 6. 24 − 40 − 120 − 200 − 280 − 340 5. 72 5. 09 4. 30 3. 33 2. 45 lmethods. eng. usf. edu http: //numerica

Example 1 Cont. Solution a) Using the forward divided difference approximation method at 7 lmethods. eng. usf. edu , http: //numerica

Example 1 Cont. Using backwards divided difference approximation method at 8 lmethods. eng. usf. edu , http: //numerica

Example 1 Cont. From the above two results it is clear that the rate of change of coefficient of thermal expansion is more at than at. b) Given 9 lmethods. eng. usf. edu http: //numerica

Example 1 Cont. Table 2 Summary of change in coefficient of thermal expansion using different approximations. Change in Coefficient of Thermal Expansion, Temperature, 10 Divided Difference Approximation 2 nd Order Polynomial Regression lmethods. eng. usf. edu http: //numerica

Direct Fit Polynomials In this method, given one can fit a data points order polynomial given by To find the first derivative, Similarly other derivatives can be found. 11 lmethods. eng. usf. edu http: //numerica

Example 2 -Direct Fit Polynomials To find contraction of a steel cylinder immersed in a bath of liquid nitrogen, one needs to know thermal expansion coefficient data as a function of temperature. This data is given for steel in Table 3. a) Using the third order polynomial interpolant, find the change in coefficient of thermal expansion at and. b) The data given in Table 3 can be regressed to to get. . Compare the results with part (a) if you used the regression curve to find the rate of change of the coefficient of thermal expansion with respect to temperature at and. 12 lmethods. eng. usf. edu http: //numerica

Example 2 Cont. Table 3 Coefficient of thermal expansion as a function of temperature. Temperature, T (o. F) 13 Coefficient of thermal expansion, α (in/in/o. F) 80 6. 47 40 6. 24 − 40 − 120 − 200 − 280 − 340 5. 72 5. 09 4. 30 3. 33 2. 45 lmethods. eng. usf. edu http: //numerica

Example 2 -Direct Fit Polynomials cont. Solution For the third order polynomial interpolation (also called cubic interpolation), we choose the coefficient of thermal expansion given by a) Change in Thermal Expansion Coefficient at : Since we want to find the rate of change in thermal expansion coefficient at , and we are using a third order polynomial, we need to choose the four points closest to that also bracket to evaluate it. The four points are 14 lmethods. eng. usf. edu http: //numerica

Example 2 -Direct Fit Polynomials cont. such that Writing the four equations in matrix form, we have 15 lmethods. eng. usf. edu http: //numerica

Example 2 -Direct Fit Polynomials cont. Solving the above four equations gives Hence 16 lmethods. eng. usf. edu http: //numerica

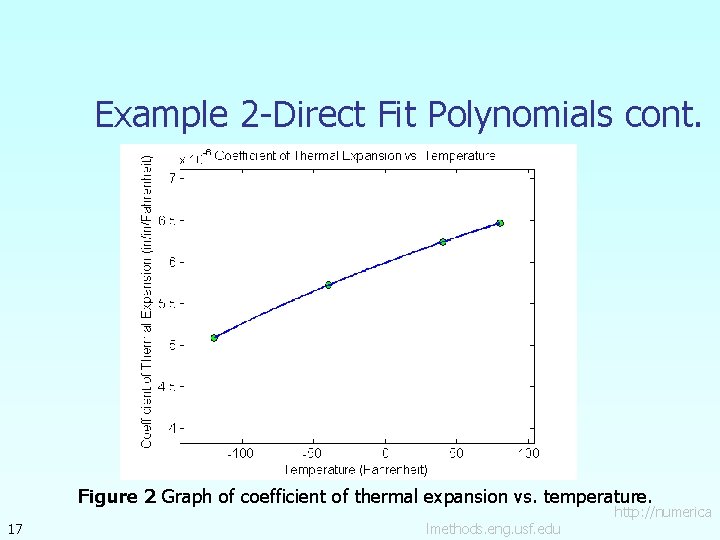
Example 2 -Direct Fit Polynomials cont. Figure 2 Graph of coefficient of thermal expansion vs. temperature. 17 lmethods. eng. usf. edu http: //numerica

Example 2 -Direct Fit Polynomials cont. The change in coefficient of thermal expansion at is given by Given that 18 lmethods. eng. usf. edu http: //numerica

Example 2 -Direct Fit Polynomials cont. b) Change in Thermal Expansion Coefficient at : Since we want to find the rate of change in thermal expansion coefficient at , and we are using a third order polynomial, we need to choose the four points closest to that also bracket to evaluate it. The four points are 19 lmethods. eng. usf. edu http: //numerica

Example 2 -Direct Fit Polynomials cont. Such that Writing the four equations in matrix form, we have 20 lmethods. eng. usf. edu http: //numerica

Example 2 -Direct Fit Polynomials cont. Solving the above four equations gives Hence 21 lmethods. eng. usf. edu http: //numerica

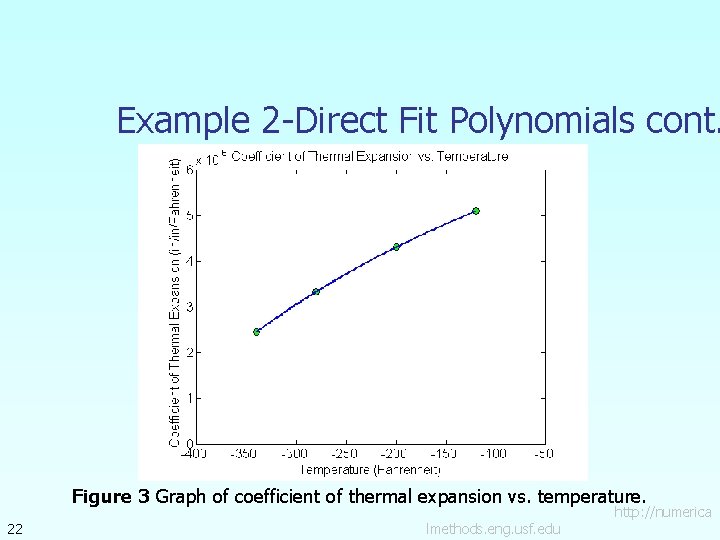
Example 2 -Direct Fit Polynomials cont. Figure 3 Graph of coefficient of thermal expansion vs. temperature. 22 lmethods. eng. usf. edu http: //numerica

Example 2 -Direct Fit Polynomials cont. The change in coefficient of thermal expansion at given by is Given that 23 lmethods. eng. usf. edu http: //numerica

Example 2 -Direct Fit Polynomials cont. Table 4 Summary of change in coefficient of thermal expansion using different approximations. Temperature, Change in Coefficient of Thermal Expansion, 3 rd Order Interpolation 24 2 nd Order Polynomial Regression lmethods. eng. usf. edu http: //numerica

Lagrange Polynomial In this method, given by where ‘ ’ in given at , one can fit a stands for the order Lagrangian polynomial order polynomial that approximates the function data points as , and a weighting function that includes a product of terms with terms of omitted. 25 lmethods. eng. usf. edu http: //numerica

Lagrange Polynomial Cont. Then to find the first derivative, one can differentiate once, and so on for other derivatives. For example, the second order Lagrange polynomial passing through is Differentiating equation (2) gives 26 lmethods. eng. usf. edu http: //numerica

Lagrange Polynomial Cont. Differentiating again would give the second derivative as 27 lmethods. eng. usf. edu http: //numerica

Example 3 To find contraction of a steel cylinder immersed in a bath of liquid nitrogen, one needs to know thermal expansion coefficient data as a function of temperature. This data is given for steel in Table 5. a) Using the second order Lagrange polynomial interpolant, find the change in coefficient of thermal expansion at and. b) The data given in Table 5 can be regressed to to get. . Compare the results with part (a) if you used the regression curve to find the rate of change of the coefficient of thermal expansion with respect to temperature at and. 28 lmethods. eng. usf. edu http: //numerica

Example 3 Cont. Table 5 Coefficient of thermal expansion as a function of temperature. Temperature, T (o. F) 29 Coefficient of thermal expansion, α (in/in/o. F) 80 6. 47 40 6. 24 − 40 − 120 − 200 − 280 − 340 5. 72 5. 09 4. 30 3. 33 2. 45 lmethods. eng. usf. edu http: //numerica

Example 3 Cont. Solution For second order Lagrangian interpolation, we choose the coefficient of thermal expansion given by a) Change in thermal expansion coefficient at : Since we want to find the rate of change in thermal expansion coefficient at and we are using second order Lagrangian interpolation, we need to choose three points closest to also bracket to evaluate it. that The three points are 30 lmethods. eng. usf. edu http: //numerica

Example 3 Cont. The change in the coefficient of thermal expansion at given by is Hence 31 lmethods. eng. usf. edu http: //numerica

Example 3 Cont. b) Change in thermal expansion coefficient at : Since we want to find the rate of change in thermal expansion coefficient at and we are using second order Lagrangian interpolation, we need to choose three points closest to that also bracket to evaluate it. The three points are The change in the coefficient of thermal expansion at given by 32 lmethods. eng. usf. edu is http: //numerica

Example 3 Cont. Hence 33 lmethods. eng. usf. edu http: //numerica

Example 3 Cont. Table 6 Summary of change in coefficient of thermal expansion using different approximations. Temperature, 34 Change in Coefficient of Thermal Expansion, 2 nd Order Lagrange Interpolation 2 nd Order Polynomial Regression lmethods. eng. usf. edu http: //numerica

Additional Resources For all resources on this topic such as digital audiovisual lectures, primers, textbook chapters, multiple-choice tests, worksheets in MATLAB, MATHEMATICA, Math. Cad and MAPLE, blogs, related physical problems, please visit http: //numericalmethods. eng. usf. edu/topics/discrete_02 dif. html

THE END http: //numericalmethods. eng. usf. edu