Differentiation Summary SUMMARY The gradient at a point


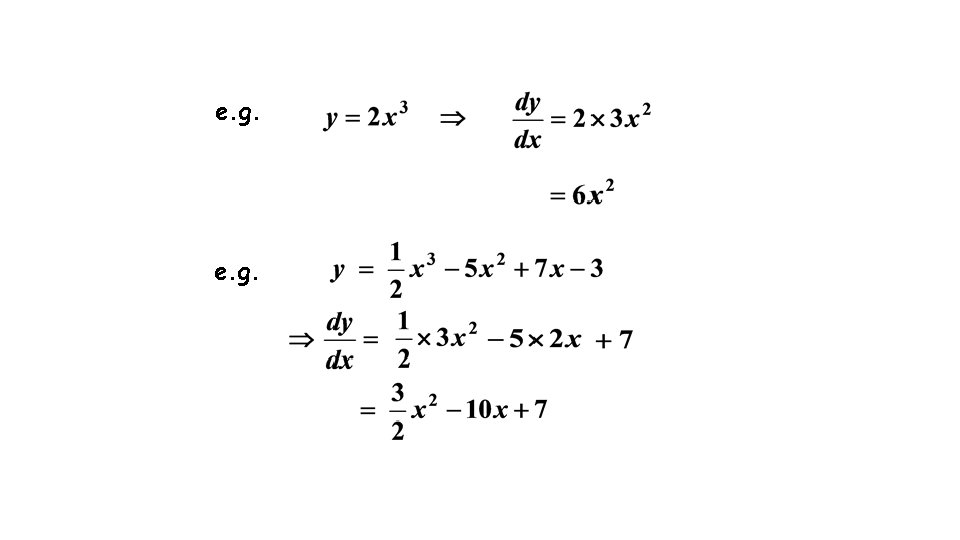






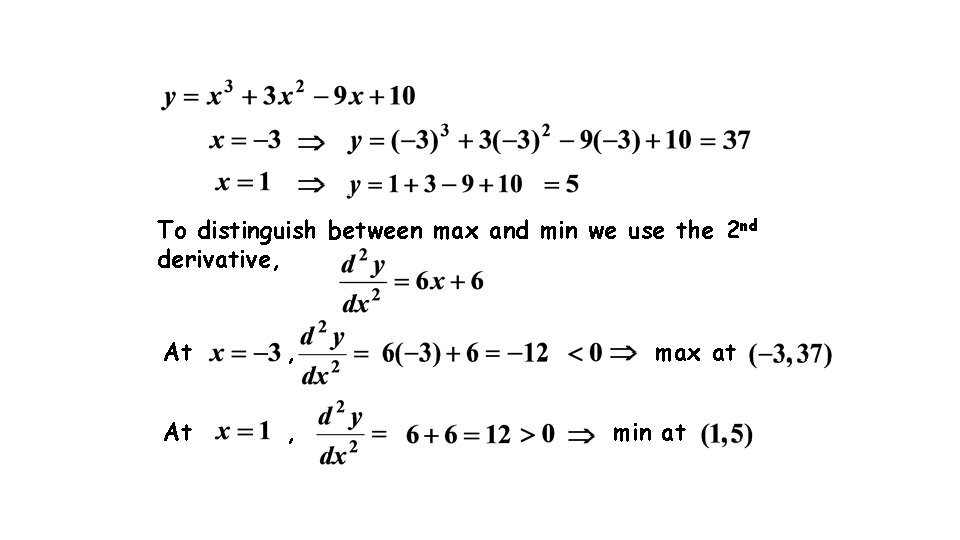



- Slides: 18

Differentiation Summary

SUMMARY Ø The gradient at a point on a curve is defined as the gradient of the tangent at that point Ø The function that gives the gradient of a curve at any point is called the gradient function Ø The process of finding the gradient function is called differentiating Ø The rule for differentiating terms of the form is • • “power to the front and multiply” “subtract 1 from the power”
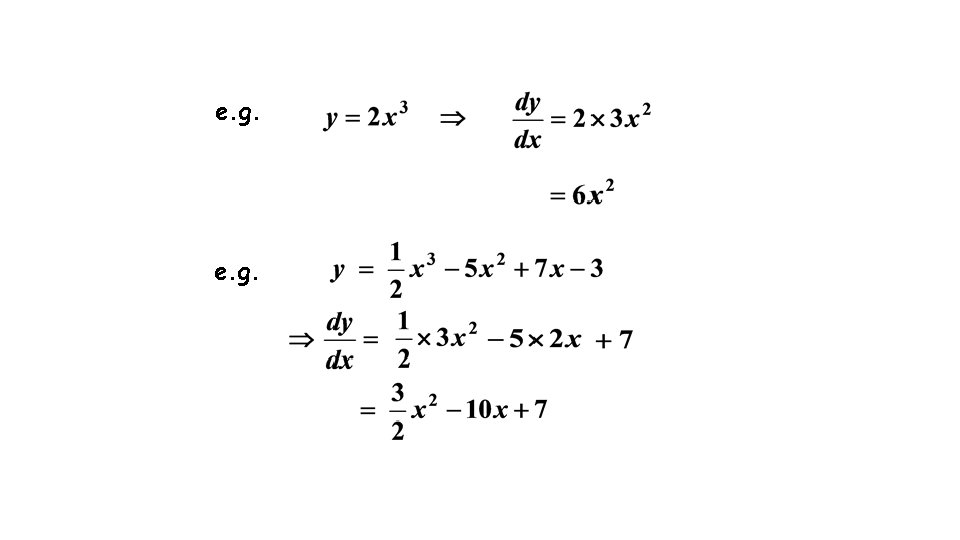
e. g.

Using Gradient Functions e. g. Find the gradient at the point where x = 1 on the curve Solution: Differentiating to find the gradient function: When x = 1, gradient m =

Exercises Find the gradients at the given points on the following curves: at the point 1. When 2. at the point When 3. at the point When

SUMMARY Ø To find the point(s) on a curve gradient: • find the gradient function • let • solve the resulting equation equal the given gradient with a given

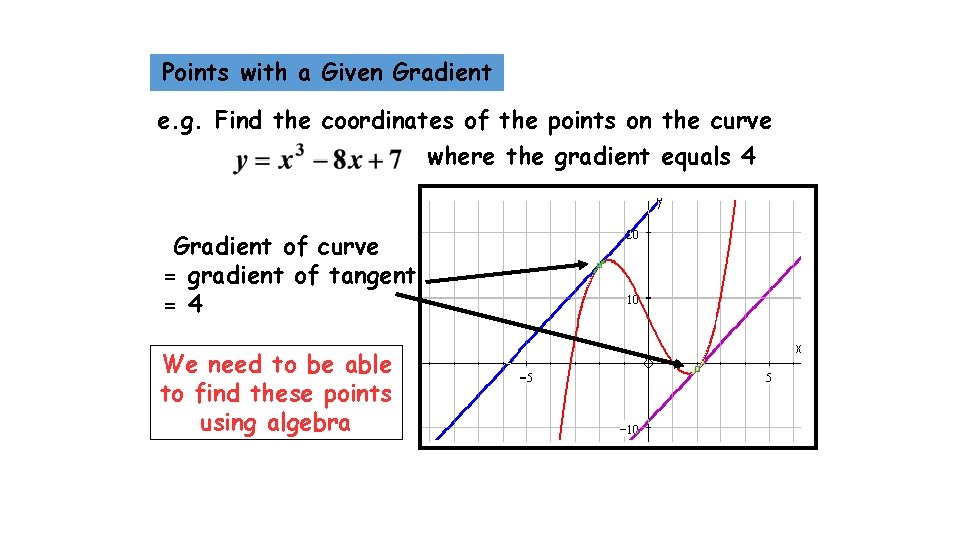
Points with a Given Gradient e. g. Find the coordinates of the points on the curve where the gradient equals 4 Gradient of curve = gradient of tangent = 4 We need to be able to find these points using algebra

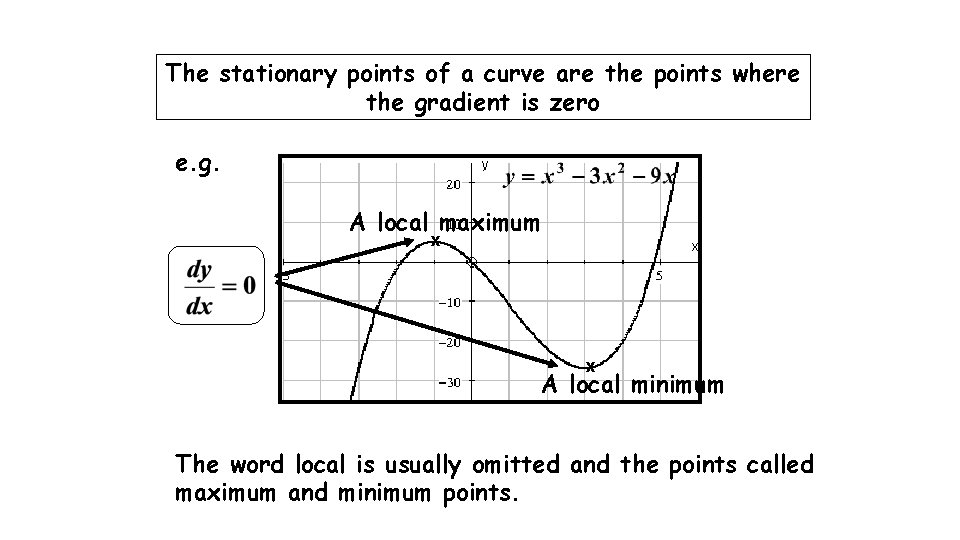
The stationary points of a curve are the points where the gradient is zero e. g. A local maximum x x A local minimum The word local is usually omitted and the points called maximum and minimum points.

e. g. 1 Find the coordinates of the stationary points on the curve Solution: or The stationary points are (3, -27) and ( -1, 5)

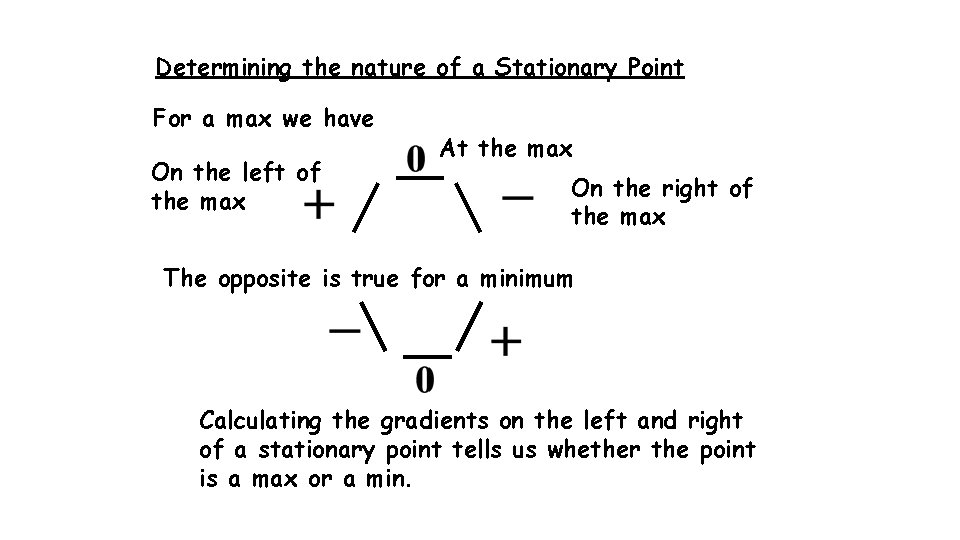
Determining the nature of a Stationary Point For a max we have On the left of the max At the max On the right of the max The opposite is true for a minimum Calculating the gradients on the left and right of a stationary point tells us whether the point is a max or a min.

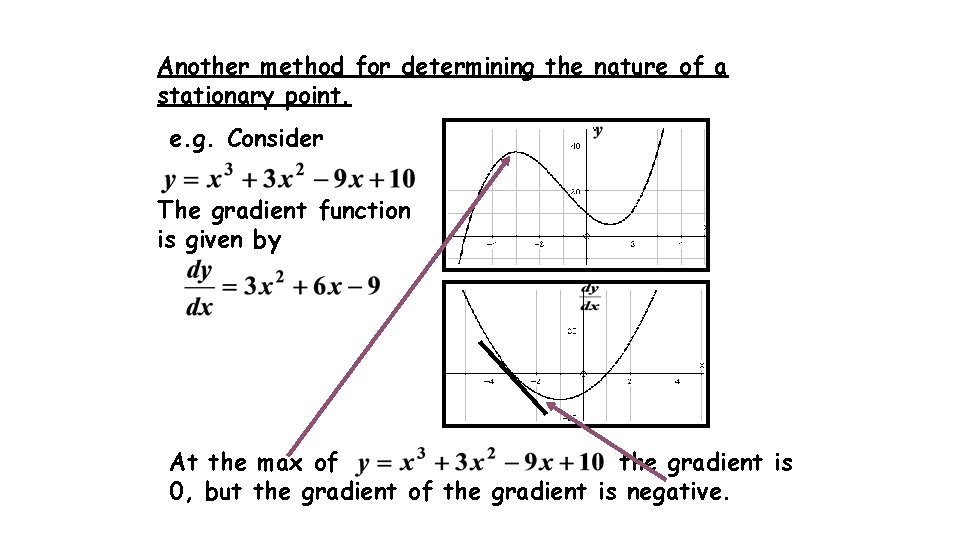
Another method for determining the nature of a stationary point. e. g. Consider The gradient function is given by At the max of the gradient is 0, but the gradient of the gradient is negative.

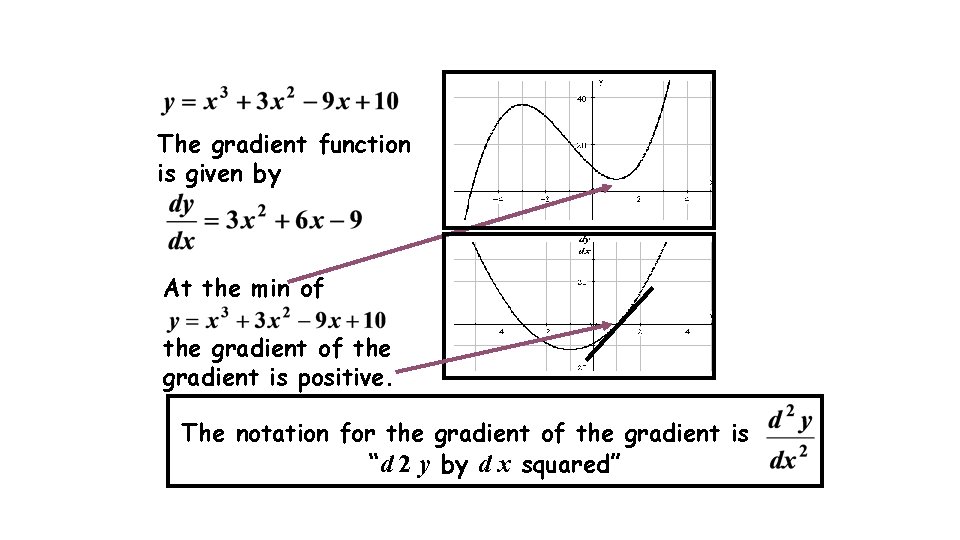
The gradient function is given by At the min of the gradient is positive. The notation for the gradient of the gradient is “d 2 y by d x squared”

The gradient of the gradient is called the 2 nd derivative and is written as

e. g. Find the stationary points on the curve and distinguish between the max and the min. Solution: Stationary points: or We now need to find the y-coordinates of the st. pts.
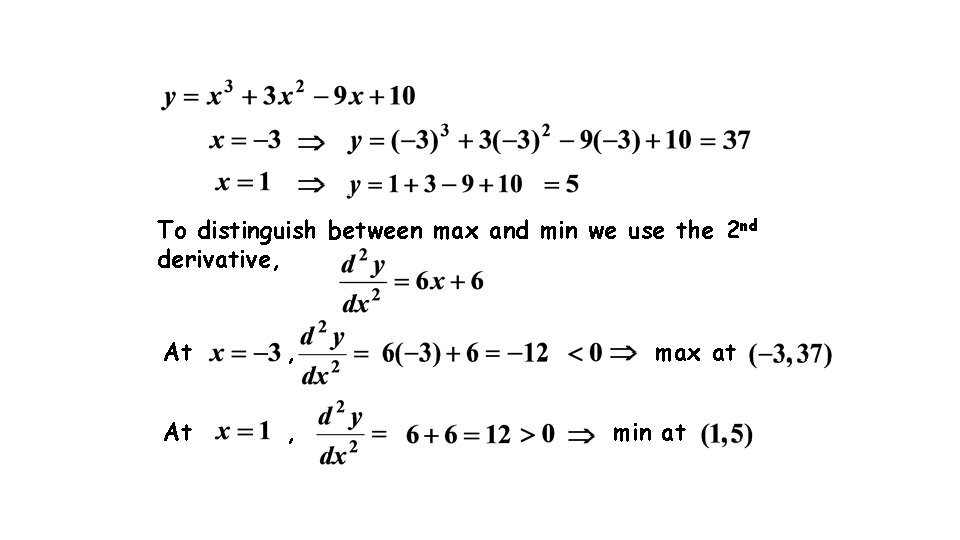
To distinguish between max and min we use the 2 nd derivative, At , max at min at

SUMMARY Ø To find stationary points, solve the equation Ø Determine the nature of the stationary points • either by finding the gradients on the left and right of the stationary points minimum • maximum or by finding the value of the 2 nd derivative at the stationary points

SUMMARY Ø COULD ALSO BE A POINT OF INFLECTION! • gradients on the left and right of the stationary points
