Differentiation Note 1 Gradients of Curves The gradient

Differentiation

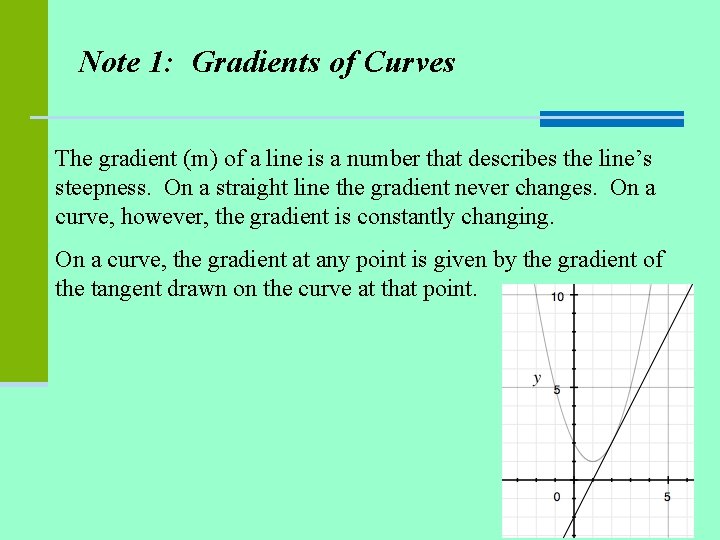
Note 1: Gradients of Curves The gradient (m) of a line is a number that describes the line’s steepness. On a straight line the gradient never changes. On a curve, however, the gradient is constantly changing. On a curve, the gradient at any point is given by the gradient of the tangent drawn on the curve at that point.

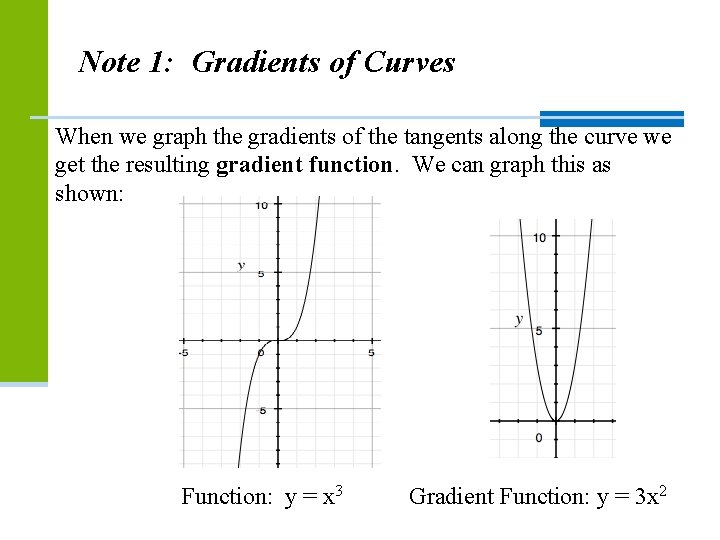
Note 1: Gradients of Curves When we graph the gradients of the tangents along the curve we get the resulting gradient function. We can graph this as shown: Function: y = x 3 Gradient Function: y = 3 x 2

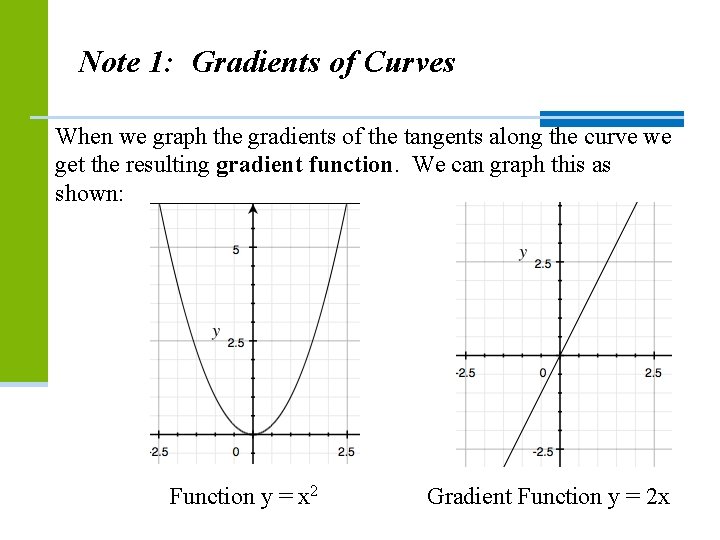
Note 1: Gradients of Curves When we graph the gradients of the tangents along the curve we get the resulting gradient function. We can graph this as shown: Function y = x 2 Gradient Function y = 2 x

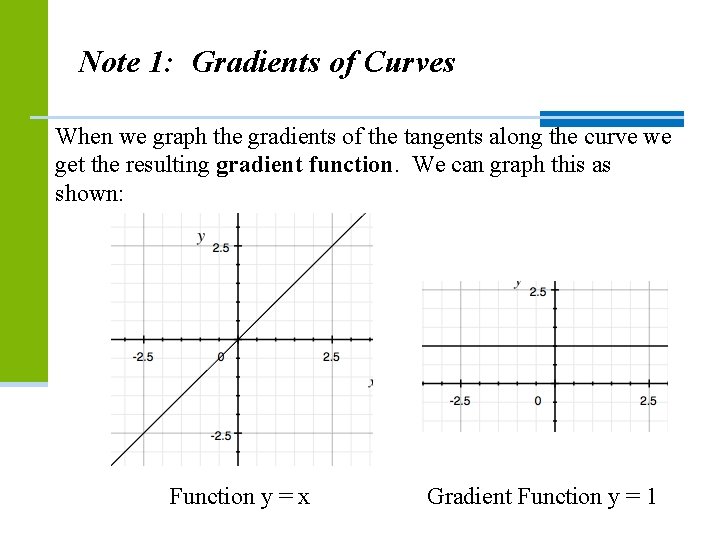
Note 1: Gradients of Curves When we graph the gradients of the tangents along the curve we get the resulting gradient function. We can graph this as shown: Function y = x Gradient Function y = 1

Note 1: Gradients of Curves The gradient function is also called the: • Derivative • Derived function Differentiating, or finding the derivative, means finding the instantaneous rate of change i. e. gradient of the tangent of a function y = f(x). Then the derivative If the Original is shown as…. . function is called…. . y y’ or f(x) f ’ or f ’ (x)

Note 2: Finding derivatives by differentiation When the curve is not given, we need another means of finding f’(x). We can do this using the function: If x is the variable; whereas a and n are constants then Examples: Find the derivatives of the following f(x) = x 4 f’(x) = 4 x 3 y = 5 x 3 + 7 x 2

Note 2: Finding derivatives by differentiation • When there is no number in front of x, a = 1 • When there is no power, n = 1, the derivative is just the number in front of x So 3 x becomes 3; – 2 x becomes – 2 etc… • When there is no x, n = 0, the derivative = 0 Constants (numbers on their own) always just become 0.

Examples: Find the derivatives of the following 1. f(x) = 3 x f’(x) = 3 There is no power, the derivative is the number in front of x 1. f(x) = 6 f’(x) = 0 There is no x, so the derivative = 0 1. f(x) = 5 x 3 – 2 x f’(x) = 15 x 2 – 2 1. f(x) = 4(x 2 + 12) = 4 x 2 + 48 f’(x) = 8 x Expand first, then differentiate

Other examples to try 1 2 3 4 15 x 4 Note the 3 and 5 are multiplied, and the original power (5) is lowered by 1 to give 4 2 x – 5 4 x – 3 If y = 3 x 2 – ½ x 4 – x , find y’. Ans: y’ = 6 x – 2 x 3 – 1 Note x 2 is treated as 1 x 2 so it becomes 2 x 1 i. e. 2 x, and 5 x just becomes 5. Note the 3 x becomes 3, and the – 7 disappears because it’s a constant. Note – the alternative phrasing of this question. y’ merely means

Note 3: Differentiating Roots and Fractional Powers • When asked to differentiate a root, first put into index form and differentiate as usual • When given a fraction where x is on the bottom, bring it to the top and make the power negative Examples: Differentiate the following

Examples: Differentiate the following 1. f(x) = = x½ f’(x) = 2. f(x) f’(x)

Examples: Differentiate the following

Note 3: Substituting into the derived function • The derivative is the gradient at any point along a curve • By substituting into the derivative the x value of the point, we can find the gradient at that point Example: Find the gradient on the curve f(x) = x 3 – 4 x 2 + 5 x – 6 at the point where x = 2 f’(x) = 3 x 2 – 8 x + 5 f’(2) = 3(2)2 – 8(2) + 5 = 12 – 16 + 5 =1 Therefore the gradient is 1 when x = 2

Note 3: Substituting into the derived function Example: The gradient at the point on the curve f(x) = x 2 – 4 x + 7 is 6. Find the co-ordinate of that point f’(x) = 2 x - 4 6 = 2 x - 4 x=5 The x co-ordinate is 5. The y co-ordinate is found by substituting this back into the original equation. f(5) = 52 – 4(5) + 7 = 12 Co-ordinate where gradient is 6 is (5, 12) Textbook: Page 535 Exercise 21. D