Differentiation Learning Objectives Understand how to differentiate ex

Differentiation Learning Objectives: §Understand how to differentiate ex §Understand how to differentiate ln ax

Differentiation Review § Differentiation means…… § Finding the gradient function. § The gradient function is used to calculate the gradient of a curve for any given value of x, so at any point.

The Key Bit The general rule (very important) is : - n x If y = dy = nxn-1 dx E. g. if y = x 2 dy = 2 x dx E. g. if y = x 3 dy = 3 x 2 dx E. g. if y = 5 x 4 dy = 5 x 4 x 3 dx dy 3 = 20 x dx

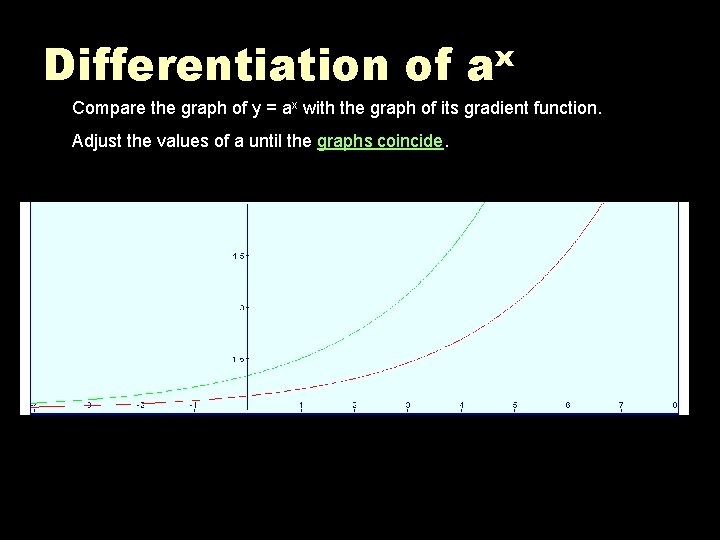
Differentiation of ax Compare the graph of y = ax with the graph of its gradient function. Adjust the values of a until the graphs coincide.

Differentiation of ax Summary The curve y = ax and its gradient function coincide when a = 2. 718 The number 2. 718…. . is called e, and is a very important number in calculus

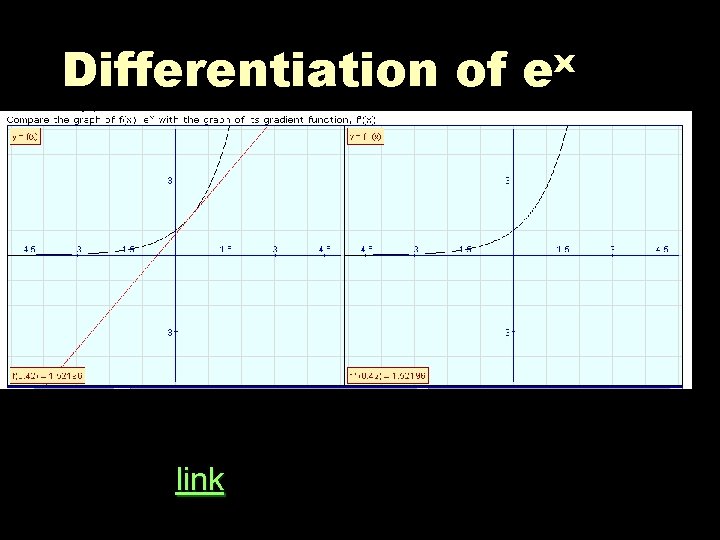
Differentiation of link x e

Differentiation of ex § The gradient function f’(x )and the original function f(x) are identical, therefore § The gradient function of ex is ex § i. e. the derivative of ex is ex If f(x) = ex Also, if f(x) = aex f ΄(x) = x e f ΄(x) = x ae

Derivative of ln x § ln x is the inverse of ex § The graph of y=ln x is a reflection of y = ex in the line y = x § This helps us to differentiate ln x § If y = ln x then x = ey so 1 = So Derivative of ln x is

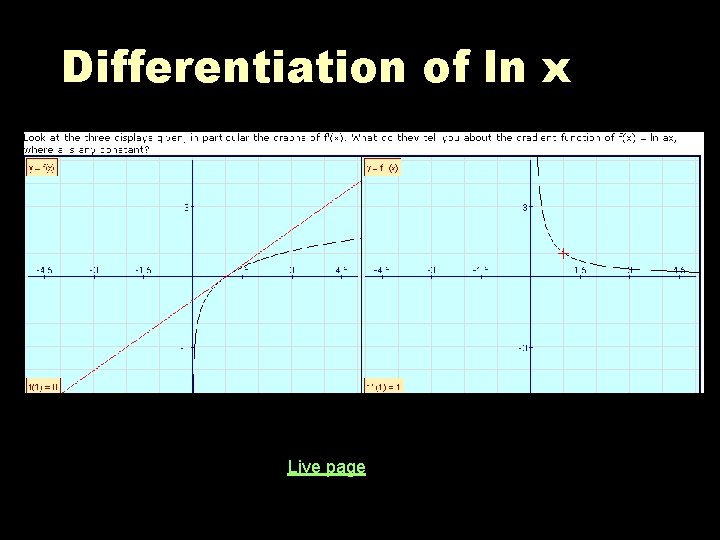
Differentiation of ln x Live page

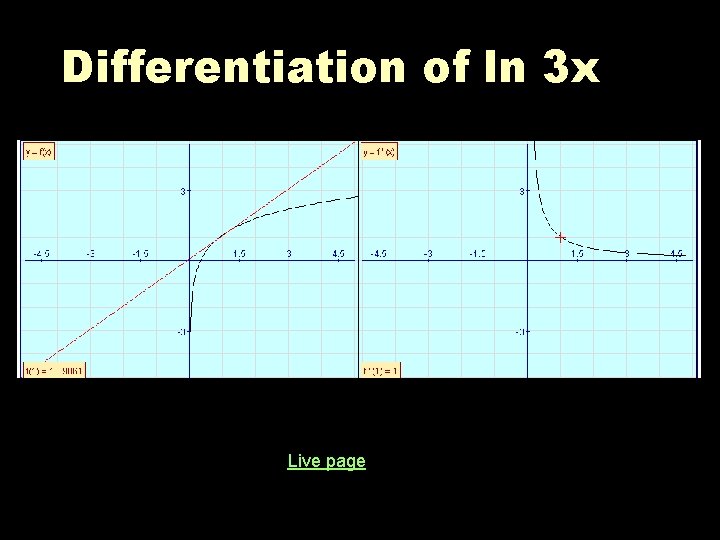
Differentiation of ln 3 x Live page

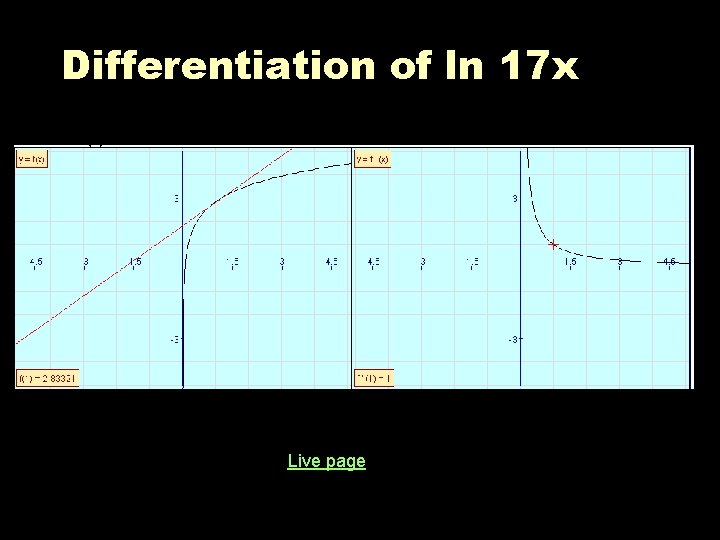
Differentiation of ln 17 x Live page

Summary - ln ax (1) f(x) = ln x f ΄(1) = 1 the gradient at x=1 is 1 f ΄(4) = 0. 25 the gradient at x=4 is 0. 25 f(x) = ln 3 x f ΄(1) = 1 the gradient at x=1 is 1 f ΄(4) = 0. 25 the gradient at x=4 is 0. 25 f(x) = ln 17 x f ΄(1) = 1 the gradient at x=1 is 1 f ΄(4) = 0. 25 the gradient at x=4 is 0. 25

Summary - ln ax (2) For f(x) = ln ax Whatever value a takes…… the gradient function is the same f ΄(1) = 1 the gradient at x=1 is 1 f ΄(4) = 0. 25 the gradient at x=4 is 0. 25 f ΄(100) = 0. 01 the gradient at x=100 is 0. 01 f ΄(0. 2) = 5 the gradient at x=0. 2 is 5 The gradient is always the reciprocal of x For f(x) = ln ax f `(x) = 1/x

Examples If f(x) = ln 7 x f `(x) = 1/x If f(x) = ln 11 x 3 Don’t know about ln ax 3 f(x) = ln 11 + ln x 3 f(x) = ln 11 + 3 ln x f ΄(x) = 3 (1/x) f ΄(x) = 3/x Constants go in differentiation

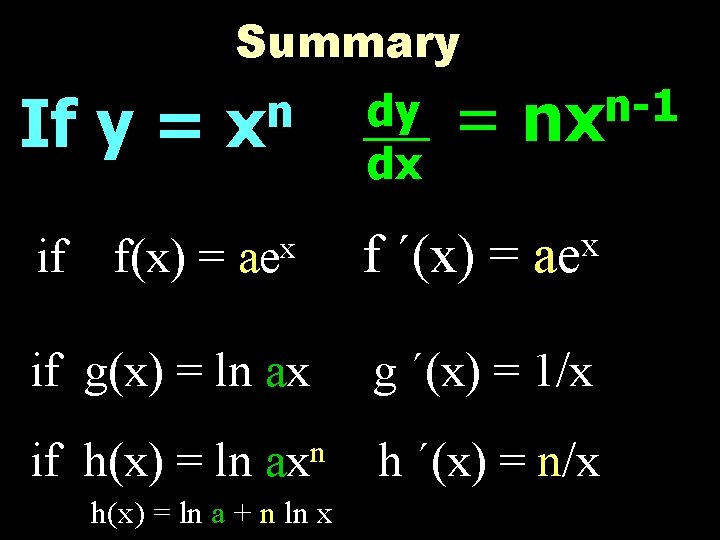
Summary If y = if f(x) = n x aex dy dx = f ΄(x) = n-1 nx x ae if g(x) = ln ax g ΄(x) = 1/x if h(x) = ln axn h ΄(x) = n/x h(x) = ln a + n ln x