Differentiation and the Derivative A derivative is obtained

Differentiation and the Derivative • A derivative is obtained through the process of differentiation, and the study of all forms of differentiation is referred to as differential calculus (likewise “integral calculus”). 1

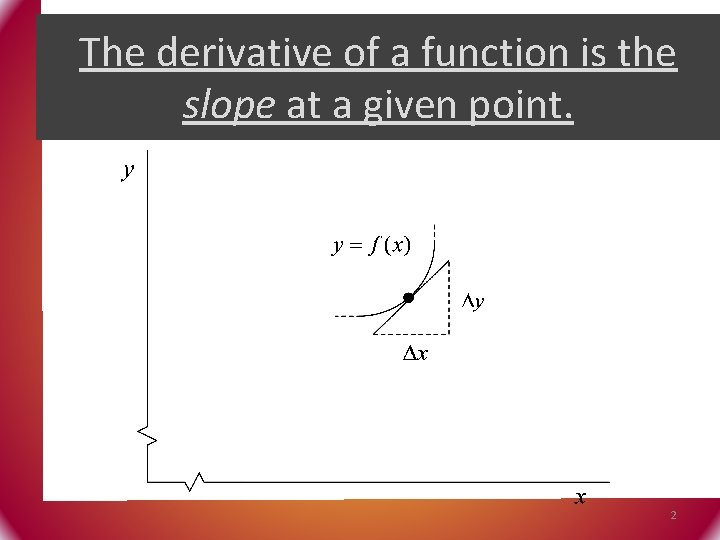
The derivative of a function is the slope at a given point. 2

Various Symbols for the Derivative 3

First Part Basic Rules of Differentiation 1. Derivative of a Constant 2. The Power Rule 3. Derivative of a Constant Multiple Function 4. The Sum Rule

Four Basic Rules • We’ve learned that to find the rule for the derivative f ′of a function f, we first find the difference quotient • But this method is tedious and time consuming, even for relatively simple functions. • Now we will develop rules that will simplify the process of finding the derivative of a function.

Derivative of a Constant • We will use the notation • To mean “the derivative of f with respect to x at x. ” • The derivative of a constant function is equal to zero.

Rule: Derivative of a Constant • We can see geometrically why the derivative of a constant must be zero. • The graph of a constant function is a straight line parallel to the x axis. • Thus, the derivative of a constant must be zero as well. y f(x) = c x

Rule: The Power Rule • If n is any real number, then

Rule: Derivative of a Constant Multiple Function • If c is any constant real number, then

Rule: The Sum Rule

Second Part Basic Rules of Differentiation 1. Product and Quotient Rules 2. Chain Rule 3. Higher Order Derivatives

The Chain Rule Simply: Differentiate the outside and then the inside

Deriving Composite Functions • Consider the function • To compute h′(x) , we can first expand h(x) and then derive the resulting polynomial • But how should we derive a function like H(x)?

Deriving Composite Functions Note that function: is a composite • H(x) is composed of two simpler functions • So that we can use this to find the derivative of H(x).

Deriving Composite Functions To find the derivative of the composite function H(x): • We let u = f(x) = x 2 + x + 1 and y = g(u) = u 100. • Then we find the derivatives of each of these functions • The ratios of these derivatives suggest that • Substituting x 2 + x + 1 for u we get

Higher Order Derivatives

Higher-Order Derivatives • The derivative f ′ of a function f is also a function. • As such, f ′ may also be differentiated. • Thus, the function f ′ has a derivative f ″ at a point x in the domain of f if the limit of the quotient exists as h approaches zero. • The function f ″ obtained in this manner is called the second derivative of the function f, just as the derivative f ′ of f is often called the first derivative of f. • By the same token, you may consider the third, fourth, fifth, etc. derivatives of a function f.

Higher-Order Derivatives Example: • Find the third derivative of the function f(x) = x 2/3 and determine its domain. Solution • We have and • So the required derivative is • The domain of the third derivative is the set of all real numbers except x = 0.

Higher-Order Derivatives Example: • Find the second derivative of the function f(x) = (2 x 2 +3)3/2 Solution • Using the general power rule we get the first derivative: