Differentiation After completing this chapter you should be

Differentiation

After completing this chapter you should be able to: • Find the gradient of a curve whose equation is expressed in a parametric form • Differentiate implicit relationships • Differentiate power functions such as ax • Use the chain rule to connect the rates of change of two variables • Set up simple differential equations from information given in context

4. 1 You can find the gradient of a curve given in parametric coordinates

1. Find the gradient of the curve with parametric equations x = t², y = 2 t³

so Exercise 4 A page 38

4. 2 You can differentiate relations which are implicit, such as x² + y² = 8 x, and cos(x + y) = siny The basic skill is to differentiate each term in turn using the chain rule and the product rule as appropriate:

Differentiating term by term gives us This gives us

Differentiating term by term From ① This gives us From ②

4. 3 You can differentiate the general power function ax, where a is constant

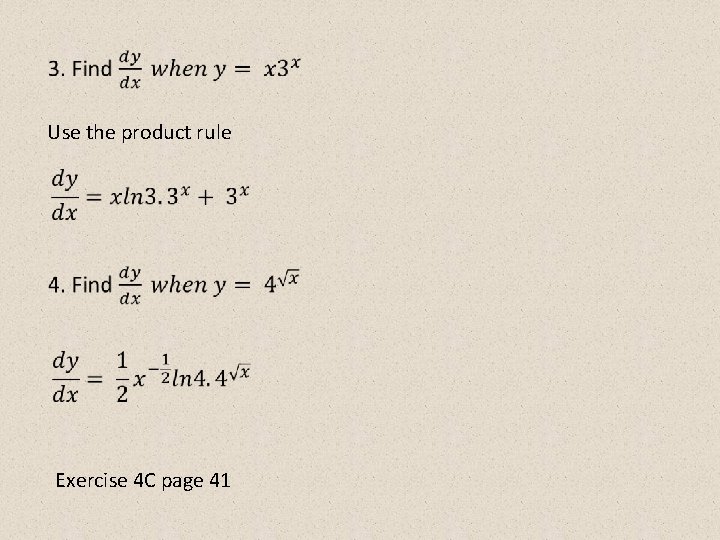
Use the product rule Exercise 4 C page 41

4. 4 You can relate one rate of change to another If a question involves two or more variables you can connect the rates of change by using the chain rule.

4. 5 You can set up a differential equation from information given in context In Core 4 we are only going to look at first order differential equations , which only involves the first derivative

A curve C has equation y = f(x) and it’s gradient at each point on the curve is directly proportional to the square of it’s y coordinate at that point. At the point (0, 3) on the curve the gradient is 1. Write down a differential equation, which could be solved to give the equation of the curve. State the value of any constant of proportionality which you use. At (0, 3) the gradient is 1

all done Exercise 4 E page 45