Differentiating Tasks Math 468 50 Sept 19 20

Differentiating Tasks Math 468. 50 Sept. 19 -20, 2008

Differentiating Instruction • “…differentiating instruction means … that students have multiple options for taking in information, making sense of ideas, and expressing what they learn. In other words, a differentiated classroom provides different avenues to acquiring content, to processing or making sense of ideas, and to developing products so that each student can learn effectively. ” Tomlinson 2001

Differentiating Instruction Some ways to differentiate instruction in mathematics class: – Open-ended Questions – Common Task with Multiple Variations – Differentiation Using Multiple Entry Points

Open-ended Questions • Open-ended questions have more than one acceptable answer and/ or can be approached by more than one way of thinking.

Open-ended Questions • Well designed open-ended problems provide most students with an obtainable yet challenging task. • Open-ended tasks allow for differentiation of product. • Products vary in quantity and complexity depending on the student’s understanding.

Open-ended Questions • An Open-Ended Question: – should elicit a range of responses – requires the student not just to give an answer, but to explain why the answer makes sense – may allow students to communicate their understanding of connections across mathematical topics – should be accessible to most students and offer students an opportunity to engage in the problem-solving process – should draw students to think deeply about a concept and to select strategies or procedures that make sense to them – can create an open invitation for interest-based student work

Open-ended Questions Method 1: Working Backward 1. Identify a topic. 2. Think of a closed question and write down the answer. 3. Make up an open question that includes (or addresses) the answer. Example: 1. Multiplication 2. 40 x 9 = 360 3. Two whole numbers multiply to make 360. What might the two numbers be?

Open-ended Questions Method 2: Adjusting an Existing Question 1. 2. 3. Identify a topic. Think of a typical question. Adjust it to make an open question. Example: 1. Money 2. How much change would you get back if you used a toonie to buy Caesar salad and juice? 3. I bought lunch at the cafeteria and got 35¢ change back. How much did I start with and what did I buy? Identify a topic. Today’s Specials Green Salad Caesar Salad Veggies and Dip Fruit Plate Macaroni Muffin Milk Juice Water $1. 15 $1. 20 $1. 15 $1. 35 65¢ 45¢ 55¢

An Open Task: Decimals • Model each decimal with base ten blocks. Make a sketch to record your work. a) O. 46 b) 3. 04 c) 1. 9 d) 1. 09 e) 3. 35 From Math Makes Sense 5, page 118 • Opening it up… • If the flat represents 1, use flats, rods and little cubes to build a robot model. Record a picture of your model and the value as a decimal number. • Repeat two more times. Share with a partner. Share with the group.

Common Task with Multiple Variations • A common problem-solving task, and adjust it for different levels • Students tend to select the numbers that are challenging enough for them while giving them the chance to be successful in finding a solution.

An Example of a Common Task with Multiple Variations • Marian has a new job. The distance she travels to work each day is {5, 94, or 114} kilometers. How many kilometers does she travel to work in {6, 7, or 9} days?

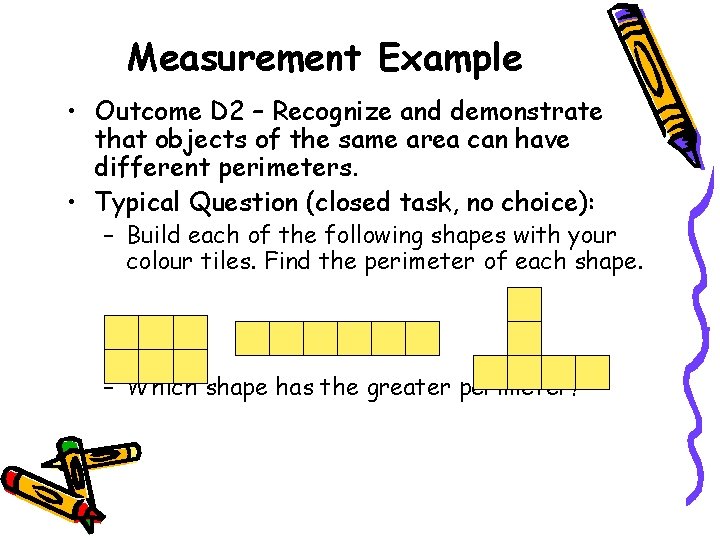
Measurement Example • Outcome D 2 – Recognize and demonstrate that objects of the same area can have different perimeters. • Typical Question (closed task, no choice): – Build each of the following shapes with your colour tiles. Find the perimeter of each shape. – Which shape has the greater perimeter?

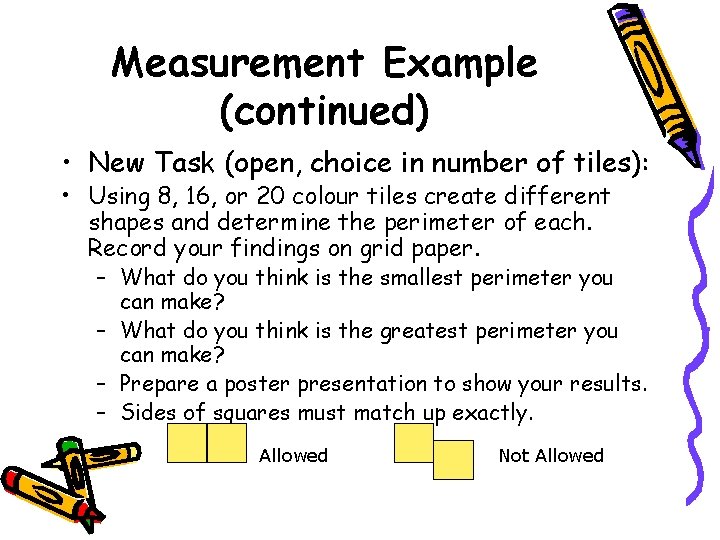
Measurement Example (continued) • New Task (open, choice in number of tiles): • Using 8, 16, or 20 colour tiles create different shapes and determine the perimeter of each. Record your findings on grid paper. – What do you think is the smallest perimeter you can make? – What do you think is the greatest perimeter you can make? – Prepare a poster presentation to show your results. – Sides of squares must match up exactly. Allowed Not Allowed

Example Spaces: Subtraction • Think of a subtraction question where the solution is a two or three digit number. • Think of another. • Think of one that is really different than the first two.

Example Spaces: Area • Think of a shape with an area of 24 cm 2. • Think of another. • Think of one that is really different than the first two.

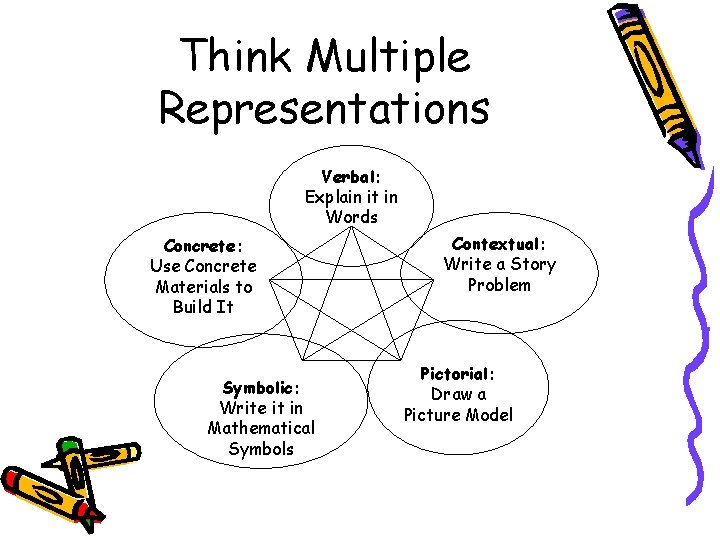
Think Multiple Representations Verbal: Explain it in Words Concrete: Use Concrete Materials to Build It Symbolic: Write it in Mathematical Symbols Contextual: Write a Story Problem Pictorial: Draw a Picture Model

Multiple Entry Points Based on Five Representations: - Concrete Real world (context) Pictures Oral and written Symbols Based on Learning Modalities: - Verbal - Auditory - Kinesthetic Based on Multiple Intelligences: - Logical-mathematical Bodily kinesthetic Linguistic Spatial Musical Naturalist Interpersonal Intrapersonal

Sample – 3 D Geometry p. 11