Differentiating ex lnx and the chain rule Objectives

Differentiating : ex, lnx and the chain rule Objectives To understand why the differentials of lnx and ex are what they are! To be able to differentiate more complex functions that are composite functions © Christine Crisp

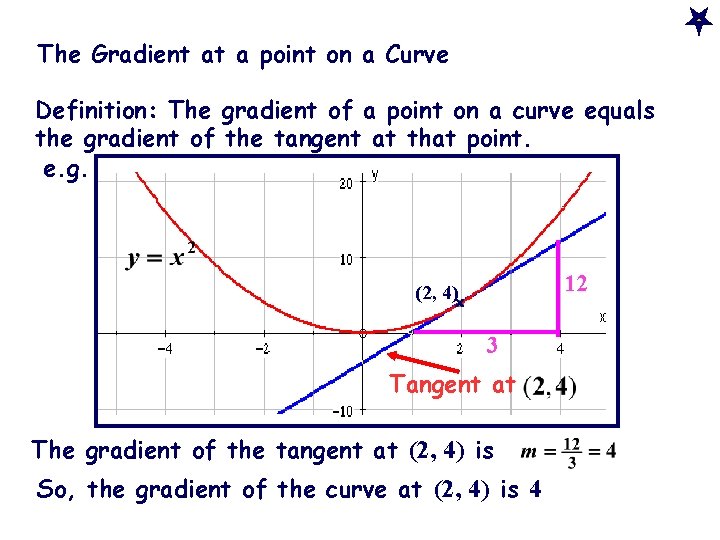
The Gradient at a point on a Curve Definition: The gradient of a point on a curve equals the gradient of the tangent at that point. e. g. 12 (2, 4)x 3 Tangent at The gradient of the tangent at (2, 4) is So, the gradient of the curve at (2, 4) is 4

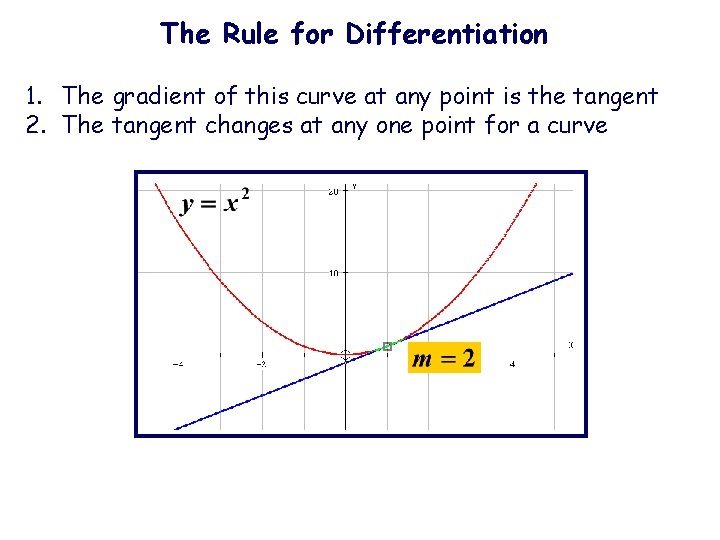
The Rule for Differentiation 1. The gradient of this curve at any point is the tangent 2. The tangent changes at any one point for a curve

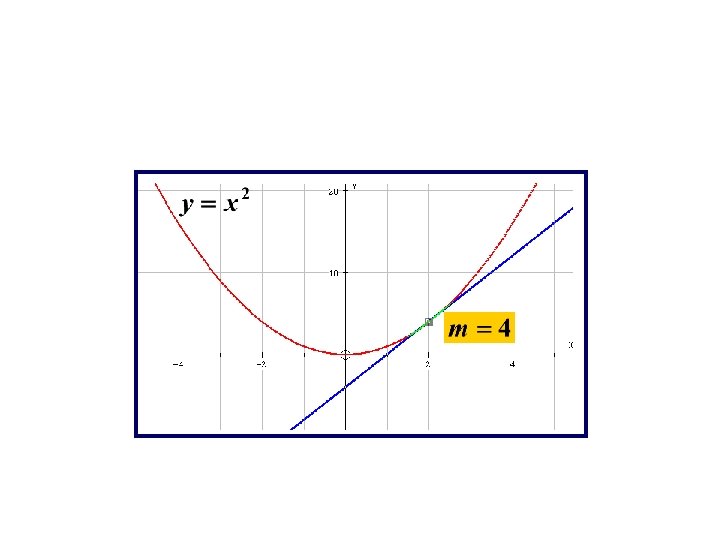
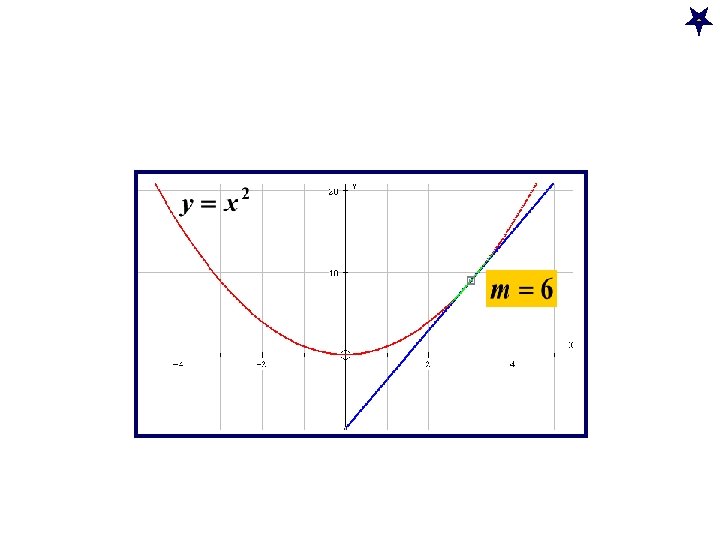
The gradient Dee-Y by Dee-X The gradient for a function is defined as Use this to show that the gradient of y=x 2 is 2 x 2 minutes for this !

Solution Like this. .

Differentiate ex and ln x From first principles This means use the definition of gradient as a limit 1 minute to think about this

Let’s consider the derivative of the exponential function. Going back to our limit definition of the derivative: First rewrite the exponential using exponent rules. Next, factor out ex. Since ex does not contain h, we can move it outside the limit.

Substituting h=0 in the limit expression results in the indeterminate form , thus we will need to determine it. We can look at the graph of and observe what happens as x gets close to 0. We can also create a table of values close to either side of 0 and see what number we are closing in on. X≠ 0 of course Graph Table x -. 1 -. 001 y. 95. 999 At x = 0, f(0) appears to be 1. As x approaches 0, y approaches 1. . 001. 01 1. 0005 1

We can safely say that from the last slide that Thus Rule 1: Derivative of the Exponential Function The derivative of the exponential function is the exponential function.

What about ln x Method 1 – Using previous result Method 2 – Consider Limits

What about ln x Method 1 – Using previous result y = ln x Method 2 – Consider Limits y = ln x f(x) = ln x therefore ey = x ( raise both sides to f(x+h) = ln (x+h) e) dx/dy = ey. (Oh yes it does!!) f'(x) = lim(h->0) [ln (x+h) - ln x] / h Since dx/dy * dy/dx = 1 = lim(h->0) ln (x+h/x) / h 1/(dx/dy) = dy/dx. = lim(h->0) 1/h * ln(1+h/x) Since lim(h->0) ln(1+h/x) -> h/x where h ≠ 0, = 1/ey f'(x) = 1/x. (as ey=x) f'(x) = 1/h * h/x = 1/x

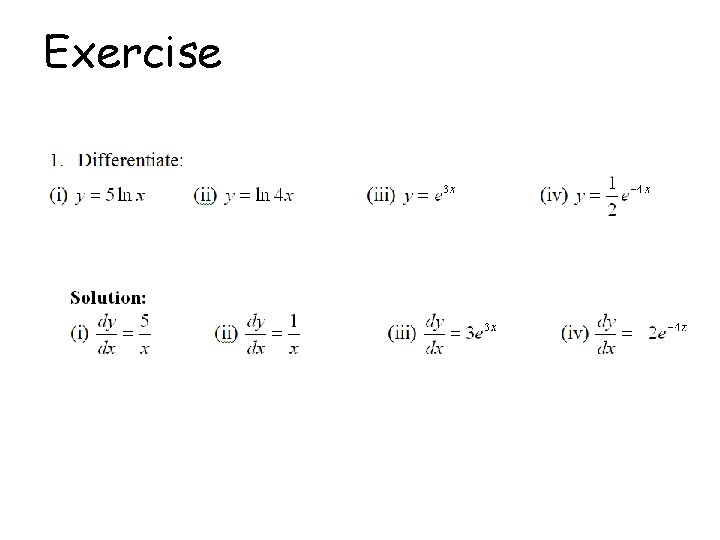
Exercise

The Chain Rule A reminder of the differentiation done so far! Ø The gradient at a point on a curve is defined as the gradient of the tangent at that point. Ø The function that gives the gradient of a curve at any point is called the gradient function. Ø The process of finding the gradient function is called differentiating. Ø The rules we have developed for differentiating are:

The Chain Rule Differentiating a function of a function Suppose . and Let We can find by multiplying out the brackets: However, the chain rule will get us to the answer without needing to do this ( essential if we had, for example, . )

The Chain Rule Consider again and 3 2 (x 4) Let . Then, Differentiating both these expressions: We must get the letters right.

The Chain Rule Consider again and 3 2 (x 4) Let . Then, Differentiating both these expressions: Now we can substitute for u

The Chain Rule Consider again and 3 2 (x 4) Let . Then, Differentiating both these expressions: Can you see how to get to the answer which we know is We need to multiply by

So, we have and to get The Chain Rule we need to multiply by So, This expression is behaving like fractions with the on the r, h, s, cancelling. ‘s

So, we have and to get The Chain Rule we need to multiply by So, This expression is behaving like fractions with the on the r, h, s, cancelling. Although these are not fractions, they come from taking the limit of the gradient, which is a fraction. s

The Chain Rule e. g. 1 Find if Solution: We need to recognise the function as and identify the inner function ( which is u ).

The Chain Rule e. g. 1 Find if Solution: We need to recognise the function as and identify the inner function ( which is u ). Let Then Differentiating: Substitute for u Tidy up by writing the constant first We don’t multiply out the brackets

The Chain Rule e. g. 2 Find if Solution: We can start in 2 ways. Can you spot them? Either write so and then let Always use fractions for indices, not decimals. Or, if you don’t notice this, start with Then

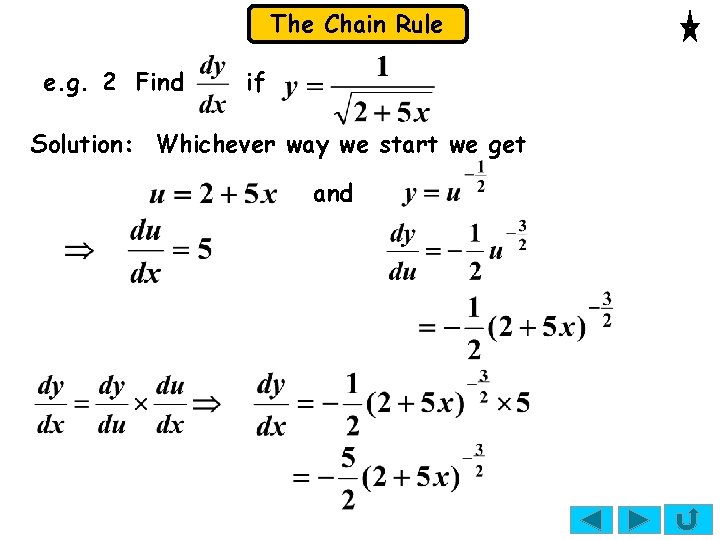
The Chain Rule e. g. 2 Find if Solution: Whichever way we start we get and

The Chain Rule SUMMARY Ø The chain rule is used for differentiating functions of a function. If where , the inner function.

The Chain Rule Exercise Use the chain rule to find 1. for the following: 2. 4. Solutions: 1. 3. 5.

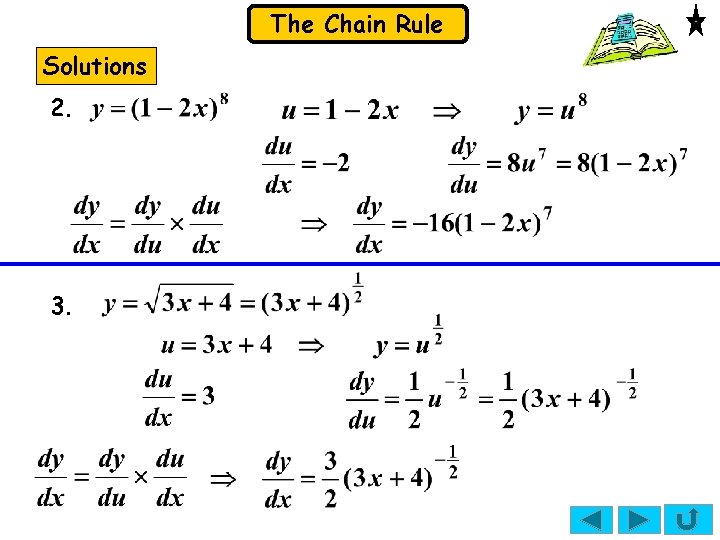
The Chain Rule Solutions 2. 3.

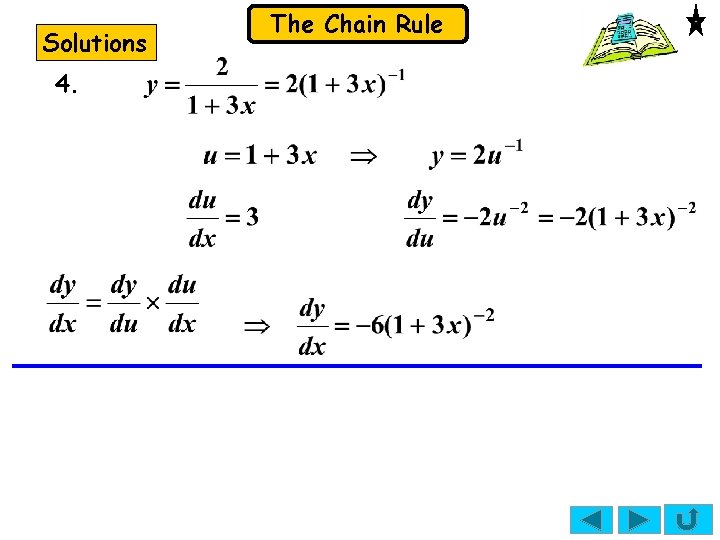
Solutions 4. The Chain Rule

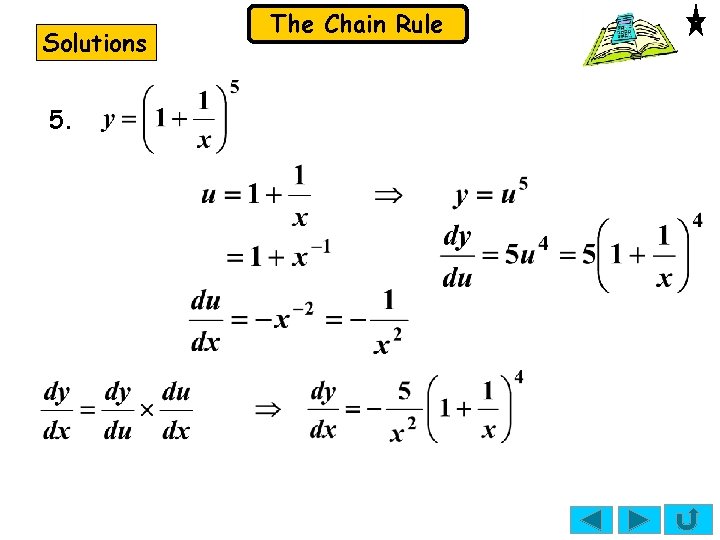
Solutions 5. The Chain Rule

The Chain Rule The chain rule can also be used to differentiate functions involving e. e. g. 3. Differentiate Solution: The inner function is the 1 st operation on x, so u = -2 x. Let

The Chain Rule Exercise Use the chain rule to differentiate the following: 1. 2. Solutions: 1. 3.

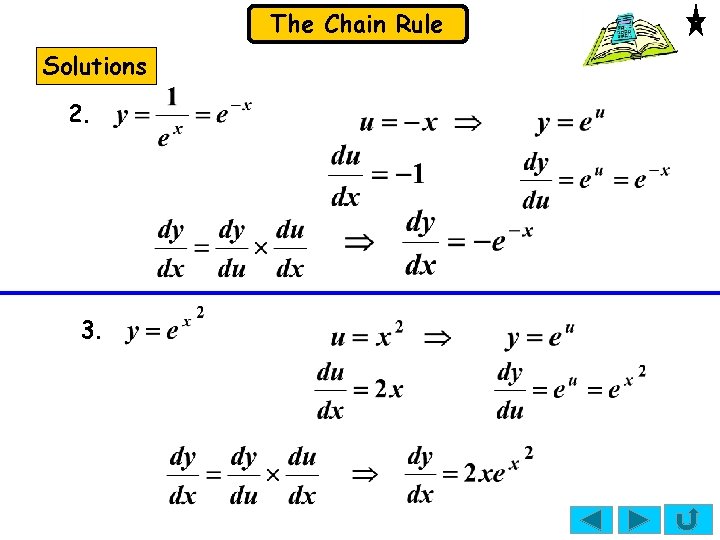
The Chain Rule Solutions 2. 3.

The Chain Rule Later we will want to reverse the chain rule to integrate some functions of a function. To prepare for this, we need to be able to use the chain rule without writing out all the steps. e. g. For we know that The derivative of the inner function which is has been multiplied by the derivative of the which is outer function ( I’ve put dashes here because we want to ignore the inner function at this stage. We must not differentiate it again. )

The Chain Rule So, the chain rule says Ø differentiate the inner function Ø multiply by the derivative of the outer function e. g.

The Chain Rule So, the chain rule says Ø differentiate the inner function Ø multiply by the derivative of the outer function e. g. ( The inner function is )

The Chain Rule So, the chain rule says Ø differentiate the inner function Ø multiply by the derivative of the outer function e. g. ( The inner function is ( The outer function is ) )

The Chain Rule Below are the exercises you have already done using the chain rule with exponential functions. See if you can get the answers directly. 1. 2. 3. Answers: 1. 2. 3. Notice how the indices never change.

The Chain Rule TIP: When you are practising the chain rule, try to write down the answer before writing out the rule in full. With some functions you will find you can do this easily. However, be very careful. With some functions it’s easy to make a mistake, so in an exam don’t take chances. It’s probably worth writing out the rule.

The Chain Rule SUMMARY Ø The chain rule is used for differentiating functions of a function. If where , the inner function.