Differential Geometric Control Theory and Applications Space and

Differential Geometric Control Theory and Applications Space and Communication Engineering Zewail City of Science and Technology Aug 16, 2016 Haithem E Taha Mechanical and Aerospace Engineering University of California, Irvine

Outline 1. What is Geometric Control? 2. Why Geometric Control? Engineering Control Payoffs from the Geometric Control Theory wak e 2

1. What is Geometric Control? - A mathematical control theory. - Concerned with dynamical systems evolving on nonlinear curvy spaces: All systems having rotational degrees of freedom. • θ 0 ≡ 2π 3

1. What is Geometric Control? - Mathematical tool to perform calculus on curvy spaces? Differential Geometry Geometric Control = Differential Geometry + Control Theory “Mechanics is the paradise of mathematical sciences, because by means of it one comes to the fruits of mathematics. ” Leonardo da Vinci 4

1. What is Geometric Control? Basic Differential Geometry • 5

2. Why Geometric Control? Engineering Control Payoffs from the Geometric Control Theory 1. Global Intrinsic Assessment of the System Behavior 2. Nonlinear Controllability and Motion Generation in Un-actuated Directions 3. Time-Varying Vector Fields and Vibrational Stabilization 6

2. Why Geometric Control? 1. Global Intrinsic Assessment of the System Behavior Attitude Control Example Task: Achieve global asymptotic stability. Feedback Control Law: Closed Loop Dynamics: But ! Bhat and Bernstein, Systems & Control Letters, 2000. There cannot exist a continuous vector field on a compact manifold that has a globally asymptotically stable equilibrium point. 7

2. Why Geometric Control? 1. Global Intrinsic Assessment of the System Behavior • 8

2. Why Geometric Control? 1. Global Intrinsic Assessment of the System Behavior • But 9

2. Why Geometric Control? 2. Nonlinear Controllability and Motion Generation in Unactuated Directions • 10

2. Why Geometric Control? 2. Nonlinear Controllability and Motion Generation in Unactuated Directions • 11

2. Why Geometric Control? 2. Nonlinear Controllability and Motion Generation in Unactuated Directions • But ! 12

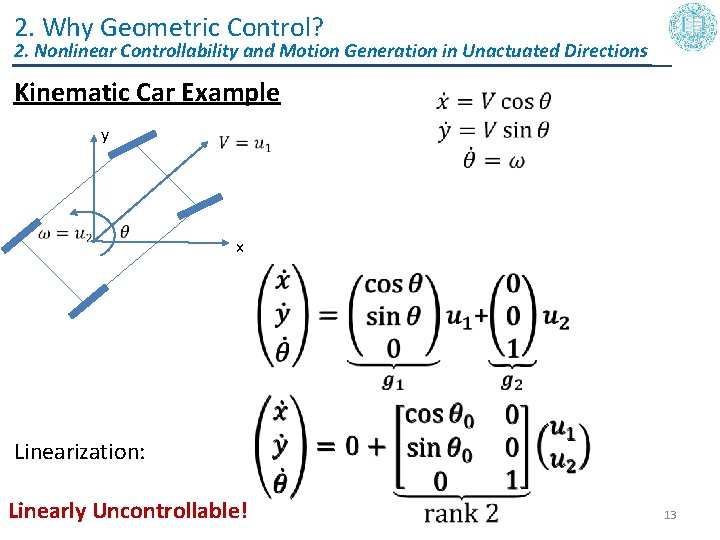
2. Why Geometric Control? 2. Nonlinear Controllability and Motion Generation in Unactuated Directions Kinematic Car Example y x Linearization: Linearly Uncontrollable! 13

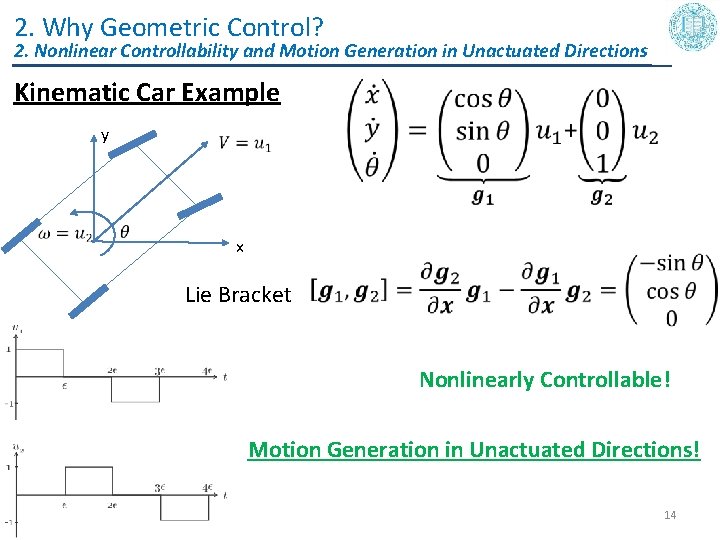
2. Why Geometric Control? 2. Nonlinear Controllability and Motion Generation in Unactuated Directions Kinematic Car Example y x Lie Bracket Nonlinearly Controllable! Motion Generation in Unactuated Directions! 14

2. Why Geometric Control? 2. Nonlinear Controllability and Motion Generation in Unactuated Directions Spacecraft Attitude Control - Three pairs of gas jets Linearly Controllable. - Two pairs of gas jets Linearly Uncontrollable. - One pair of gas jets Linearly Uncontrollable. - Geometric Nonlinear Analysis: Crouch, IEEE Transactions on Automatic Control, 1984. The system is still controllable with only one pair of gas jets. What about Airplane Controllability in case of “loss-of -control”? Hassan and Taha, AIAA GNC 2016. 15

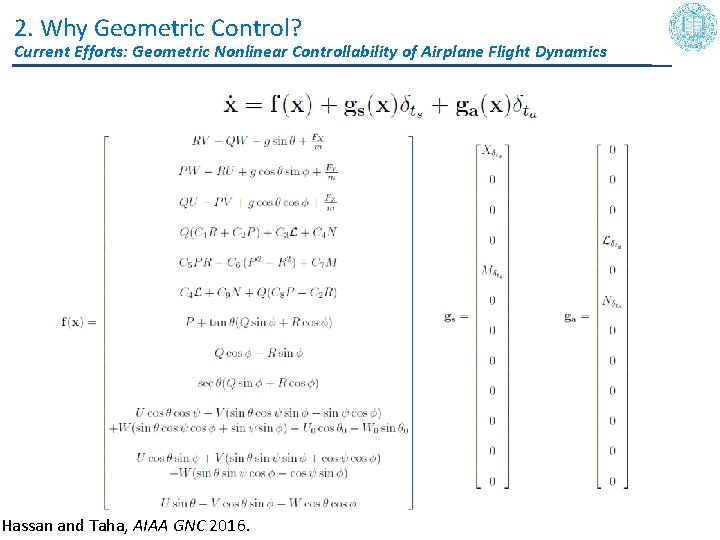
2. Why Geometric Control? Current Efforts: Geometric Nonlinear Controllability of Airplane Flight Dynamics Loss of Hydraulics Turkish Airlines 1974 United Airlines 1989 DHL 2003 16

2. Why Geometric Control? Current Efforts: Geometric Nonlinear Controllability of Airplane Flight Dynamics Hassan and Taha, AIAA GNC 2016.

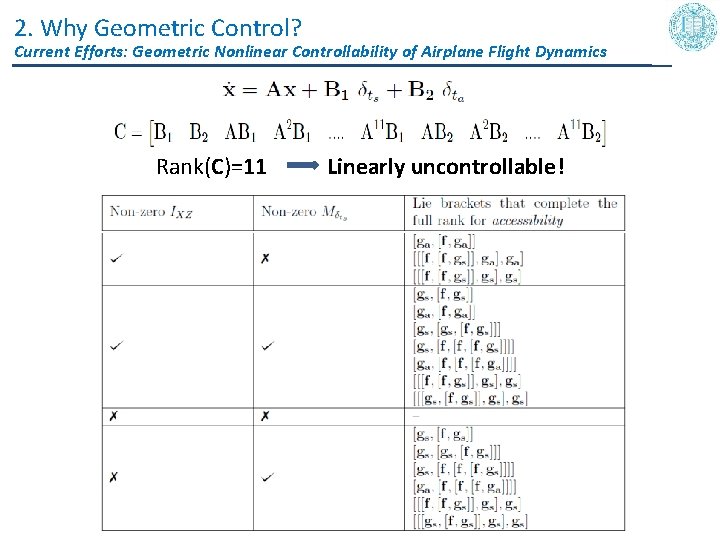
2. Why Geometric Control? Current Efforts: Geometric Nonlinear Controllability of Airplane Flight Dynamics Rank(C)=11 Linearly uncontrollable!

2. Why Geometric Control? Current Efforts: Geometric Nonlinear Controllability of Airplane Flight Dynamics Hassan and Taha, AIAA GNC 2016.

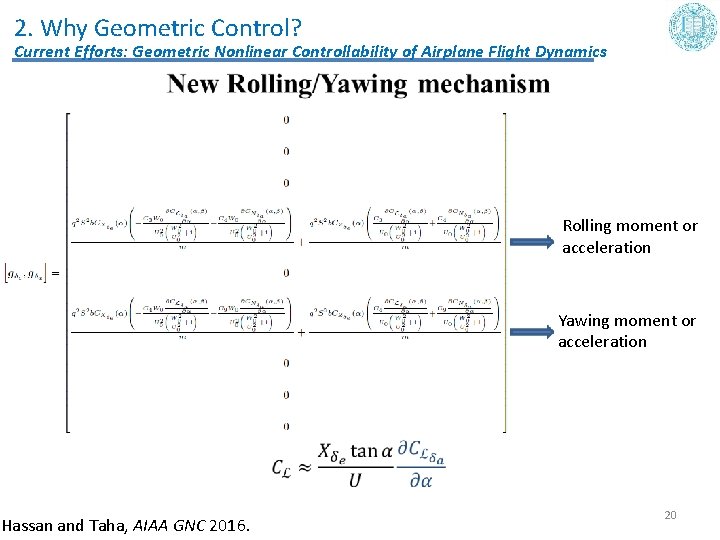
2. Why Geometric Control? Current Efforts: Geometric Nonlinear Controllability of Airplane Flight Dynamics • Rolling moment or acceleration Yawing moment or acceleration Hassan and Taha, AIAA GNC 2016. 20

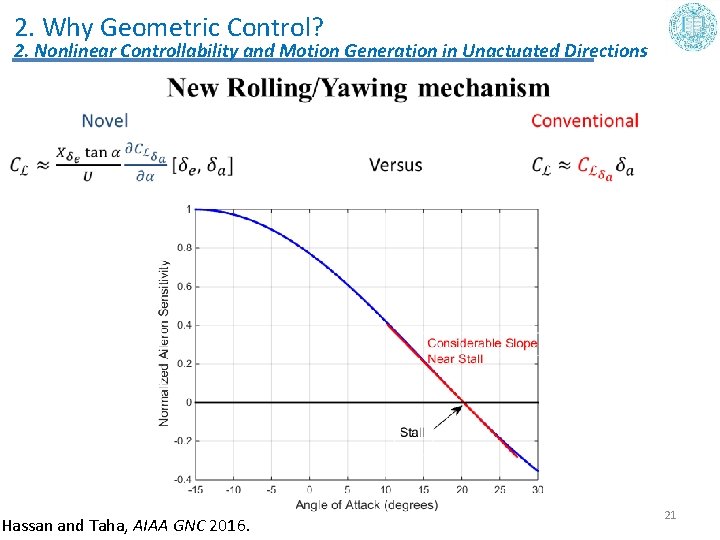
2. Why Geometric Control? 2. Nonlinear Controllability and Motion Generation in Unactuated Directions • Hassan and Taha, AIAA GNC 2016. 21

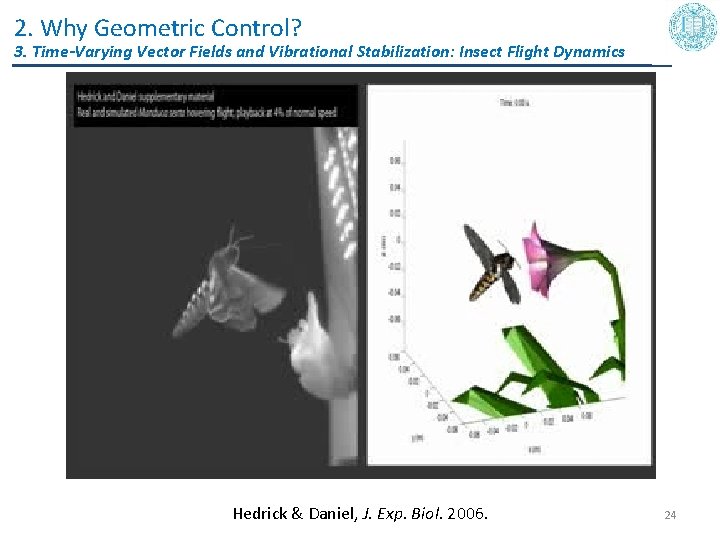
2. Why Geometric Control? 3. Time-Varying Vector Fields and Vibrational Stabilization: Insect Flight Dynamics wak e Hedrick & Daniel, J. Exp. Biol. 2006. 24

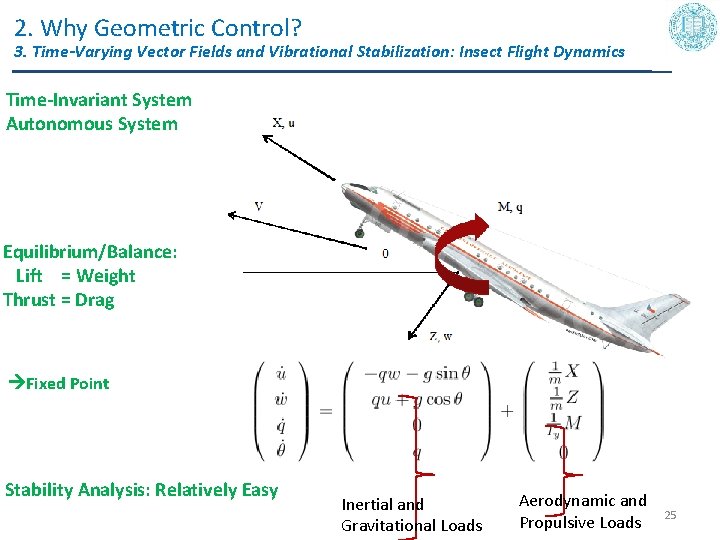
2. Why Geometric Control? 3. Time-Varying Vector Fields and Vibrational Stabilization: Insect Flight Dynamics Time-Invariant System Autonomous System Equilibrium/Balance: Lift = Weight Thrust = Drag wak e Fixed Point Stability Analysis: Relatively Easy Inertial and Gravitational Loads Aerodynamic and Propulsive Loads 25

2. Why Geometric Control? 3. Time-Varying Vector Fields and Vibrational Stabilization: Insect Flight Dynamics - Neglect Wing flexibility. Neglect Wing Inertia. But ! Essentially Time-Periodic Aerodynamic Loads Time-Varying System Non-autonomous System Equilibrium/Balance: No Fixed Point can be achieved for all times. Rather a periodic orbit. Stability Analysis? ? 26

2. Why Geometric Control? 3. Time-Varying Vector Fields and Vibrational Stabilization: Insect Flight Dynamics Taha et al. , JGCD 2013. 27

2. Why Geometric Control? 3. Time-Varying Vector Fields and Vibrational Stabilization: Insect Flight Dynamics Time-Invariant System Autonomous System Equilibrium/Balance: Average Lift = Weight Fixed point at the origin: Hovering Stability Analysis: Taylor et al. 1999 -2006 Sun et al. 2005 -2008 Cheng and Deng 2011 Insects are unstable at hover. Taha et al. , JGCD 2013. 28

2. Why Geometric Control? 3. Time-Varying Vector Fields and Vibrational Stabilization: Insect Flight Dynamics But ! Taha et al. , JGCD 2013. How small is small enough? ! 29

2. Why Geometric Control? 3. Time-Varying Vector Fields and Vibrational Stabilization “To many physicists and astronomers averaging seems to be such a natural procedure that they do not even bother to justify the process. However it is important to have a rigorous approximation theory, since it is precisely the fact that averaging seems so natural that obscures the pitfalls and restrictions of the method” Sanders and Verhulst wak e 30

2. Why Geometric Control? 3. Vibrational Stabilization First-order averaging (direct): Second-order averaging: Agrachev & Gamkrelidze, Mathematics of the USSR 1979: Exponential Representation of Flows and Chronological calculus Sarychev, 2001 and Vela, 2003: Complete Averaging 31

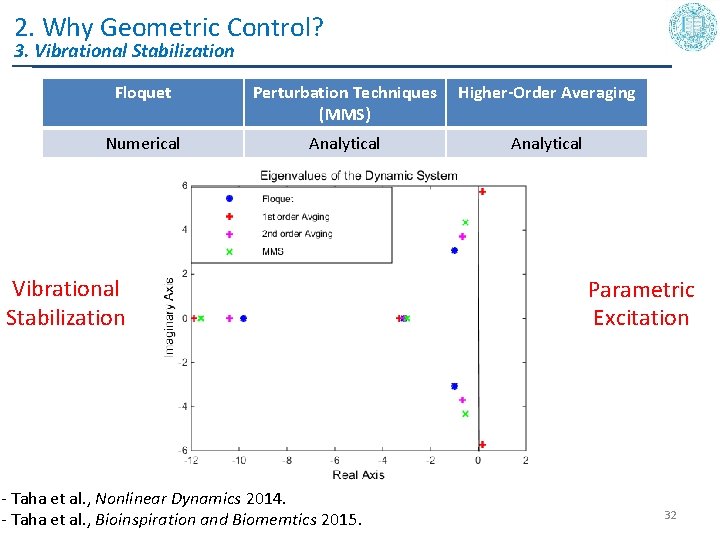
2. Why Geometric Control? 3. Vibrational Stabilization Floquet Perturbation Techniques (MMS) Higher-Order Averaging Numerical Analytical Vibrational Stabilization - Taha et al. , Nonlinear Dynamics 2014. - Taha et al. , Bioinspiration and Biomemtics 2015. Parametric Excitation 32

2. Why Geometric Control? 3. Vibrational Stabilization First-order averaging (direct): Second-order averaging: Taha et al. , Bioinspiration and Biomemtics 2015. 33

2. Why Geometric Control? 3. Vibrational Stabilization Similar Spring Action 34

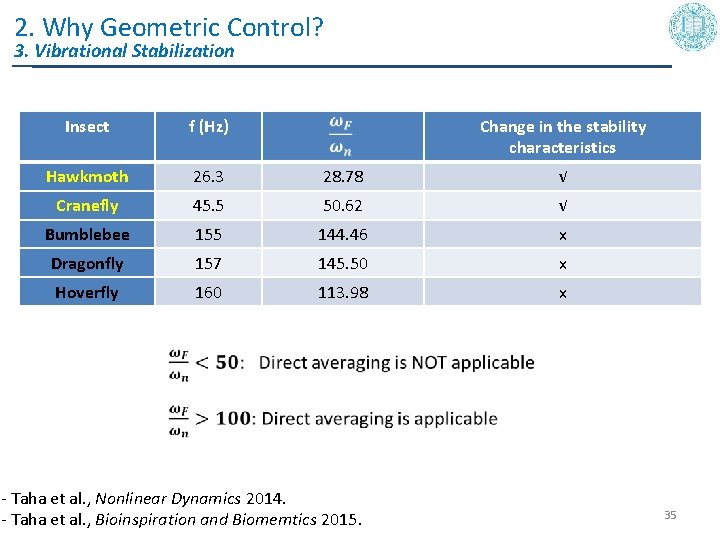
2. Why Geometric Control? 3. Vibrational Stabilization Insect f (Hz) Change in the stability characteristics Hawkmoth 26. 3 28. 78 √ Cranefly 45. 5 50. 62 √ Bumblebee 155 144. 46 x Dragonfly 157 145. 50 x Hoverfly 160 113. 98 x - Taha et al. , Nonlinear Dynamics 2014. - Taha et al. , Bioinspiration and Biomemtics 2015. 35

Conclusion - Geometric Control = Differential Geometry + Control Theory - Engineering Control Payoffs from the Geometric Control Theory 1. Global Intrinsic Assessment of the System Behavior 2. Generation of Motion in Unactuated Directions 3. Time-Varying Vector Fields and Vibrational Stabilization 36

Differential Geometric Control Theory and Applications Thank You! Haithem E Taha Mechanical and Aerospace Engineering University of California, Irvine