Differential Evolution DE and its Variant Enhanced DE

Differential Evolution (DE) and its Variant Enhanced DE (EDE) Presented By: Ayesha Zafar Student of MS(CS) Research Domain: Energy Management in Smart Grid Supervised By: Dr. Nadeem Javaid

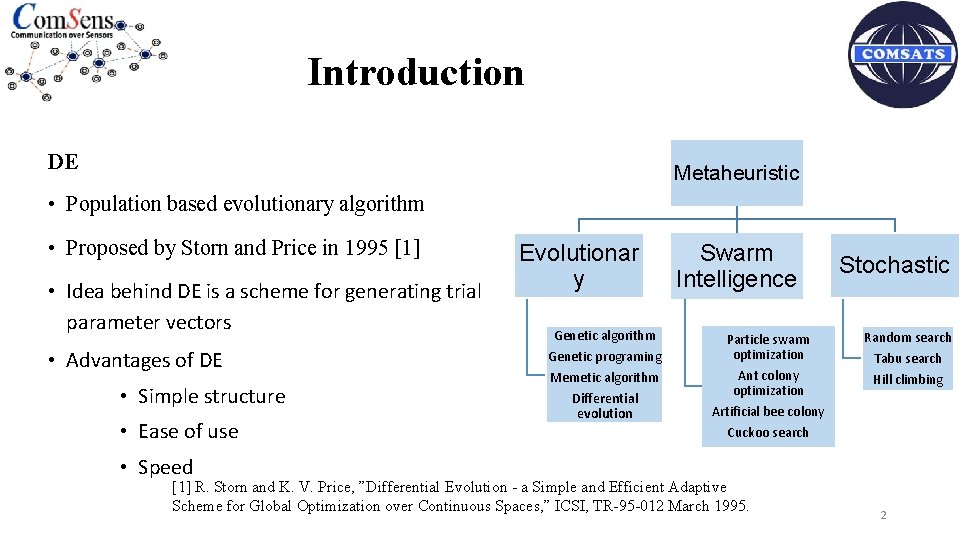
Introduction DE Metaheuristic • Population based evolutionary algorithm • Proposed by Storn and Price in 1995 [1] • Idea behind DE is a scheme for generating trial parameter vectors • Advantages of DE • Simple structure • Ease of use Evolutionar y Genetic algorithm Genetic programing Memetic algorithm Differential evolution Swarm Intelligence Stochastic Particle swarm optimization Random search Tabu search Ant colony optimization Artificial bee colony Cuckoo search Hill climbing • Speed [1] R. Storn and K. V. Price, ”Differential Evolution - a Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces, ” ICSI, TR-95 -012 March 1995. 2

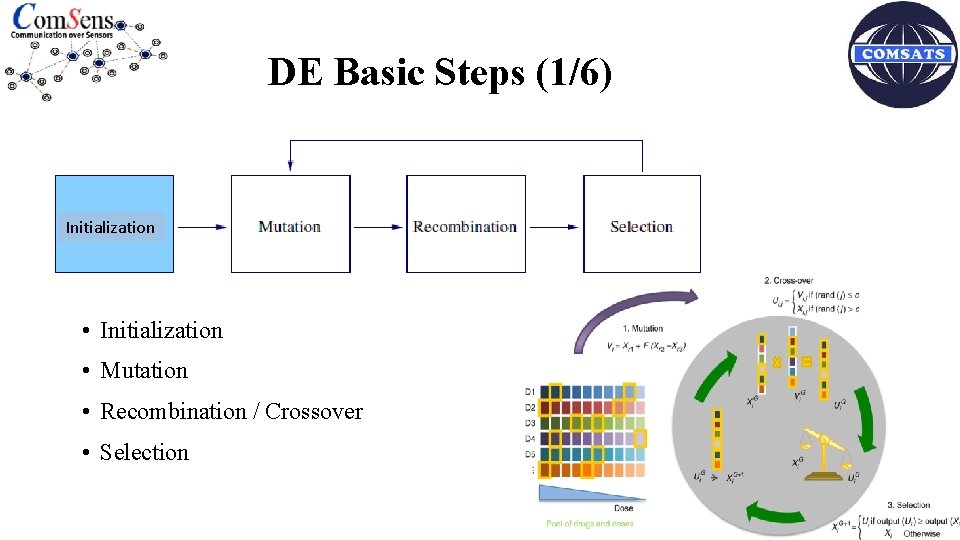
DE Basic Steps (1/6) Initialization • Initialization • Mutation • Recombination / Crossover • Selection 3

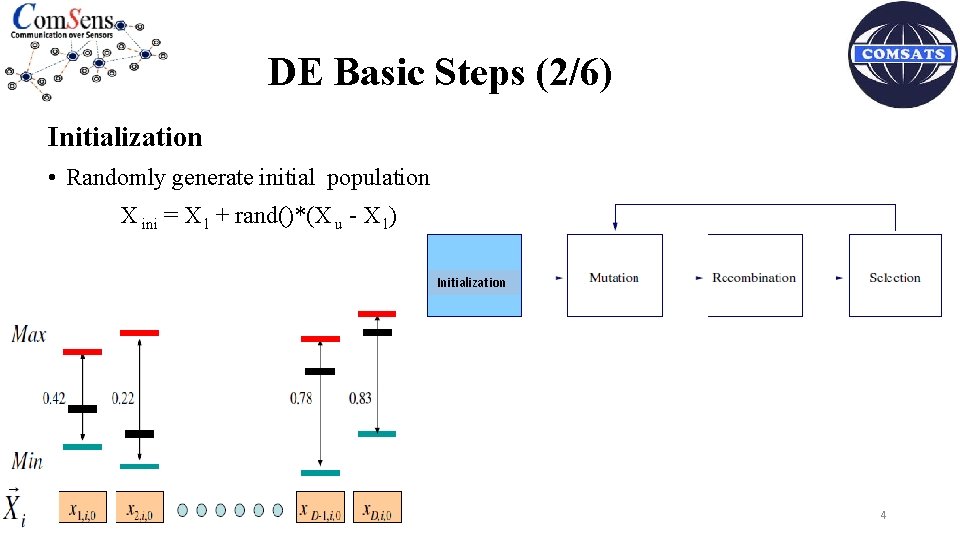
DE Basic Steps (2/6) Initialization • Randomly generate initial population X ini = X l + rand()*(X u - X l) Initialization 4

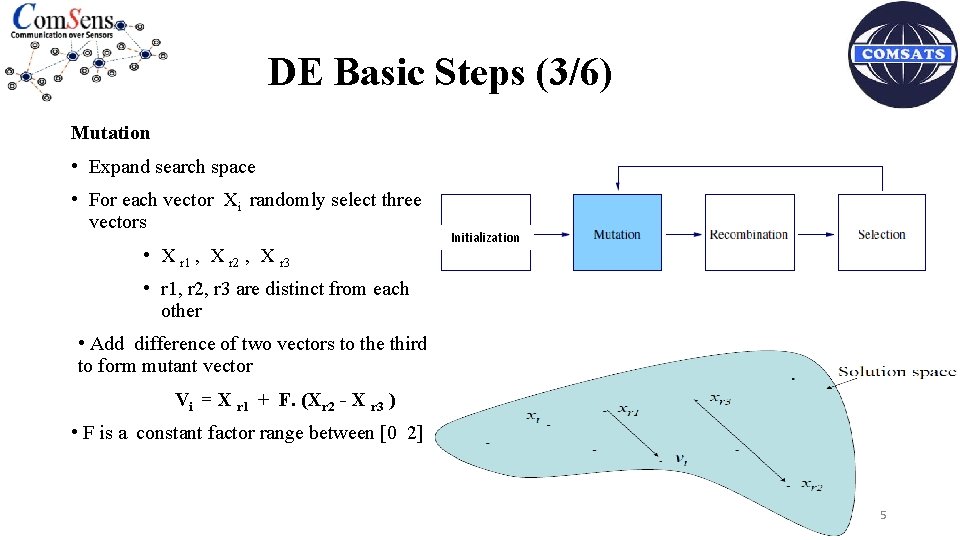
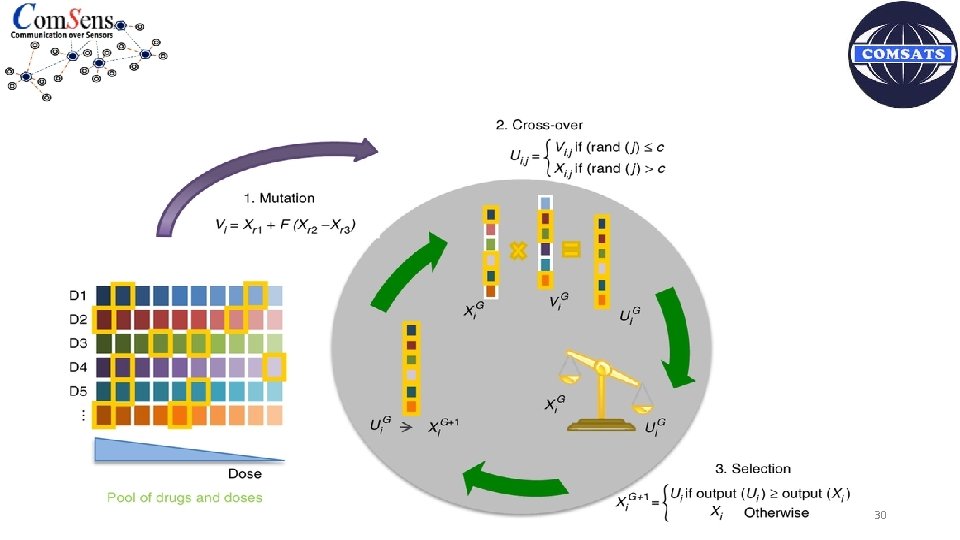
DE Basic Steps (3/6) Mutation • Expand search space • For each vector Xi randomly select three vectors • X r 1 , X r 2 , X r 3 Initialization • r 1, r 2, r 3 are distinct from each other • Add difference of two vectors to the third to form mutant vector Vi = X r 1 + F. (Xr 2 - X r 3 ) • F is a constant factor range between [0 2] 5

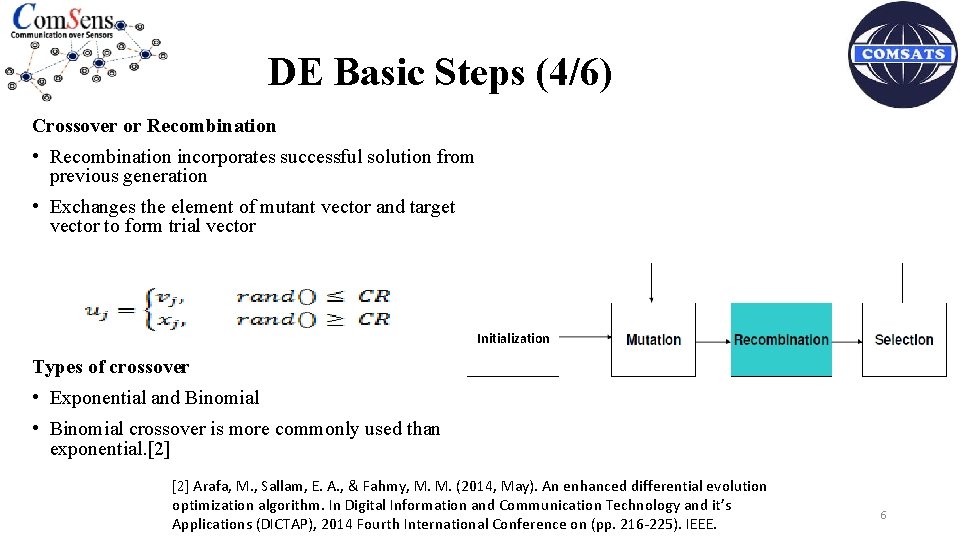
DE Basic Steps (4/6) Crossover or Recombination • Recombination incorporates successful solution from previous generation • Exchanges the element of mutant vector and target vector to form trial vector Initialization Types of crossover • Exponential and Binomial • Binomial crossover is more commonly used than exponential. [2] Arafa, M. , Sallam, E. A. , & Fahmy, M. M. (2014, May). An enhanced differential evolution optimization algorithm. In Digital Information and Communication Technology and it’s Applications (DICTAP), 2014 Fourth International Conference on (pp. 216 -225). IEEE. 6

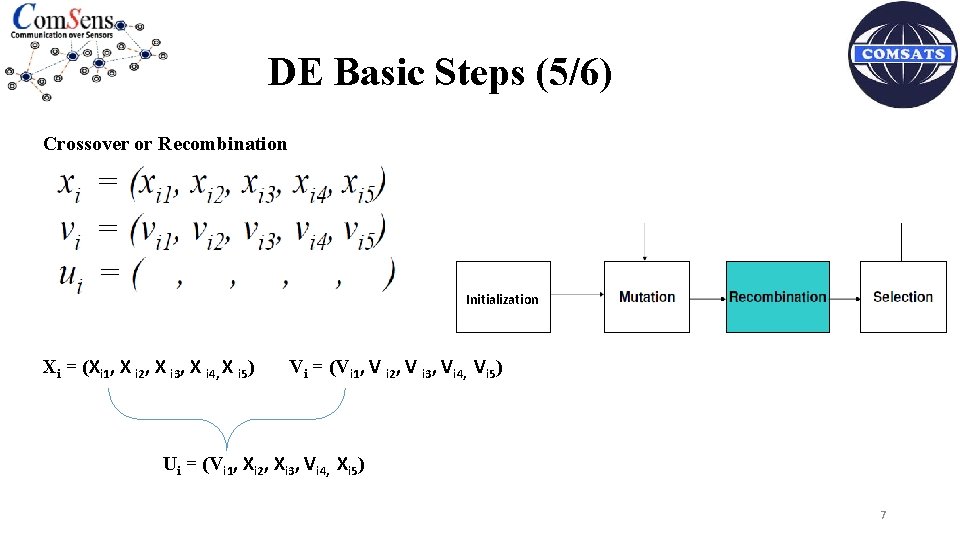
DE Basic Steps (5/6) Crossover or Recombination Initialization Xi = (Xi 1, X i 2, X i 3, X i 4, X i 5) Vi = (Vi 1, V i 2, V i 3, Vi 4, Vi 5) Ui = (Vi 1, Xi 2, Xi 3, Vi 4, Xi 5) 7

DE Basic Steps (6/6) Selection • Survival of the fittest solution • Compare target vector with trial vector, one with the better fitness admitted to the next generation • Mutation, crossover and selection continue until some stopping criteria reaches 8

Example DE (1/5) • Consider following two dimensional function f (x, y) = x 2 + y 2 • Start with a population of 5 candidates randomly initiated in the range [-10, 10] Initial population X 1, 0 (2, -1) X 2, 0 (6, 1) X 3, 0 (-3, 5) X 4, 0 (-2, 6) X 5, 0 (6, -7) 9

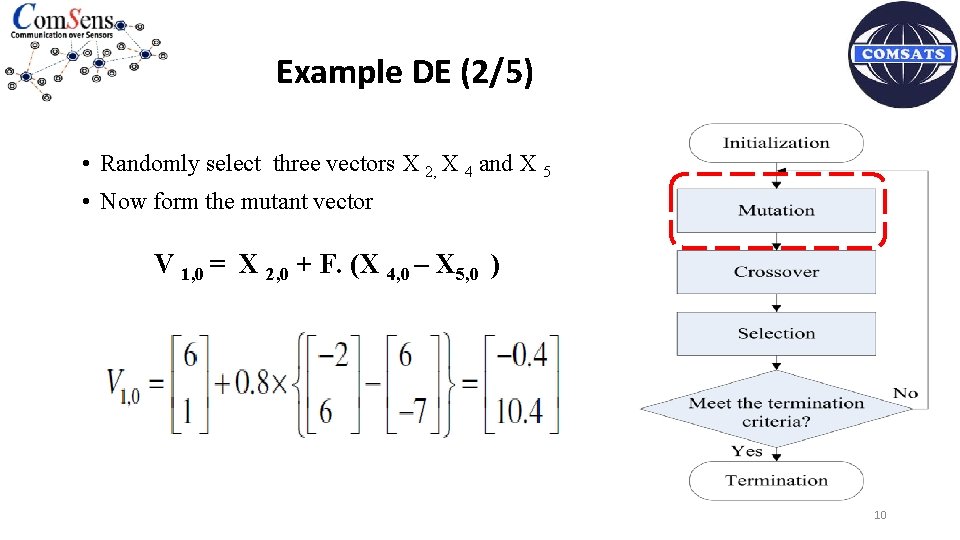
Example DE (2/5) • Randomly select three vectors X 2, X 4 and X 5 • Now form the mutant vector V 1, 0 = X 2, 0 + F. (X 4, 0 – X 5, 0 ) 10

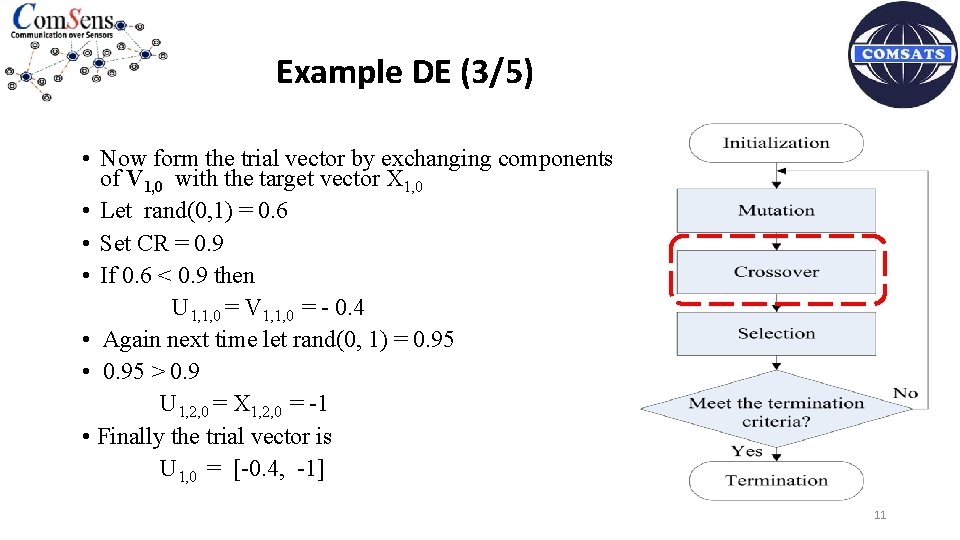
Example DE (3/5) • Now form the trial vector by exchanging components of V 1, 0 with the target vector X 1, 0 • Let rand(0, 1) = 0. 6 • Set CR = 0. 9 • If 0. 6 < 0. 9 then U 1, 1, 0 = V 1, 1, 0 = - 0. 4 • Again next time let rand(0, 1) = 0. 95 • 0. 95 > 0. 9 U 1, 2, 0 = X 1, 2, 0 = -1 • Finally the trial vector is U 1, 0 = [-0. 4, -1] 11

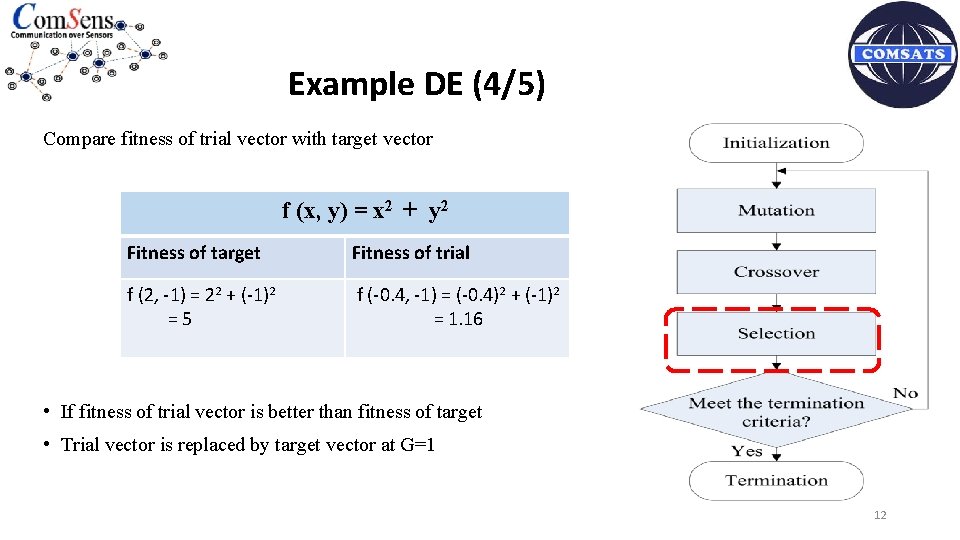
Example DE (4/5) Compare fitness of trial vector with target vector f (x, y) = x 2 + y 2 Fitness of target Fitness of trial f (2, -1) = 22 + (-1)2 =5 f (-0. 4, -1) = (-0. 4)2 + (-1)2 = 1. 16 • If fitness of trial vector is better than fitness of target • Trial vector is replaced by target vector at G=1 12

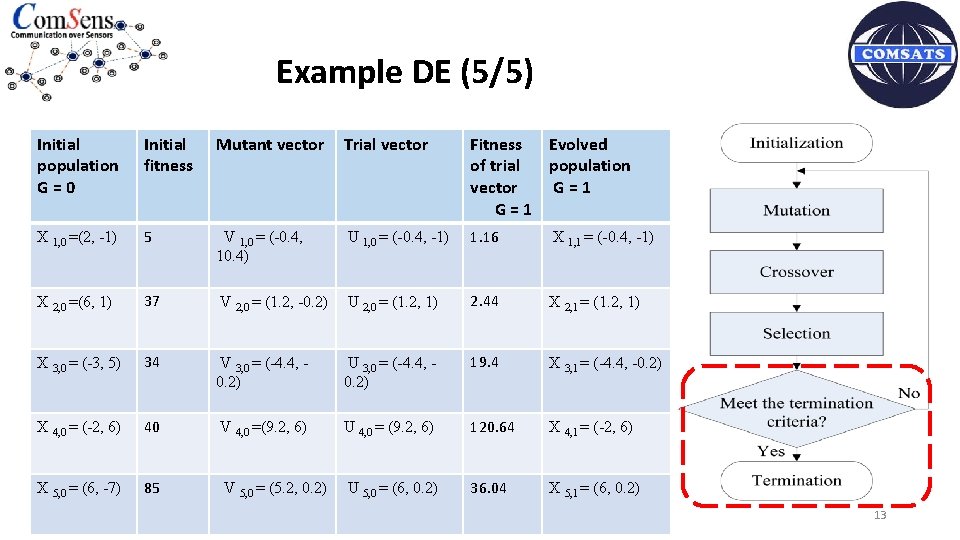
Example DE (5/5) Initial population G=0 Initial fitness Mutant vector Trial vector Fitness Evolved of trial population vector G=1 X 1, 0 =(2, -1) 5 V 1, 0 = (-0. 4, 10. 4) U 1, 0 = (-0. 4, -1) 1. 16 X 1, 1 = (-0. 4, -1) X 2, 0 =(6, 1) 37 V 2, 0 = (1. 2, -0. 2) U 2, 0 = (1. 2, 1) 2. 44 X 2, 1 = (1. 2, 1) X 3, 0 = (-3, 5) 34 V 3, 0 = (-4. 4, 0. 2) U 3, 0 = (-4. 4, 0. 2) 19. 4 X 3, 1 = (-4. 4, -0. 2) X 4, 0 = (-2, 6) 40 V 4, 0 =(9. 2, 6) U 4, 0 = (9. 2, 6) 120. 64 X 4, 1 = (-2, 6) X 5, 0 = (6, -7) 85 V 5, 0 = (5. 2, 0. 2) U 5, 0 = (6, 0. 2) 36. 04 X 5, 1 = (6, 0. 2) 13

Enhanced DE (EDE) Introduction • Developed in 2014 [2] • Improve trial vector strategy • Increase accuracy • Create five different trial vectors • First three trail vectors are obtained by taking three different crossover rates • 0. 3, 0. 6 and 0. 9 instead of one in case of DE • Fourth trial vector increase its convergence speed • Last trial vector increases diversity of search space [2] Arafa, M. , Sallam, E. A. , & Fahmy, M. M. (2014, May). An enhanced differential evolution optimization algorithm. In Digital Information and Communication Technology and it’s Applications (DICTAP), 2014 Fourth International Conference on (pp. 216 -225). IEEE. 14

Enhanced DE (EDE) • 15

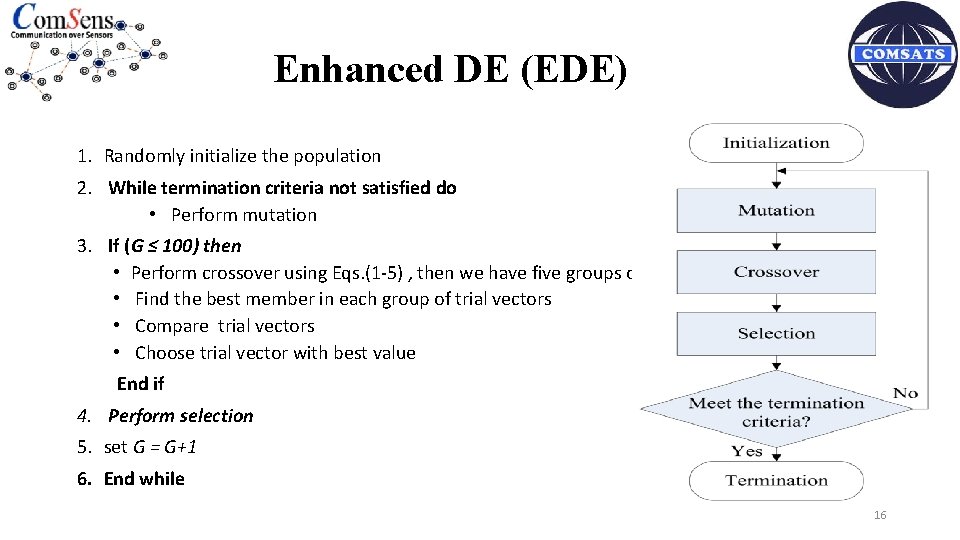
Enhanced DE (EDE) 1. Randomly initialize the population 2. While termination criteria not satisfied do • Perform mutation 3. If (G ≤ 100) then • Perform crossover using Eqs. (1 -5) , then we have five groups of trial vectors • Find the best member in each group of trial vectors • Compare trial vectors • Choose trial vector with best value End if 4. Perform selection 5. set G = G+1 6. End while 16

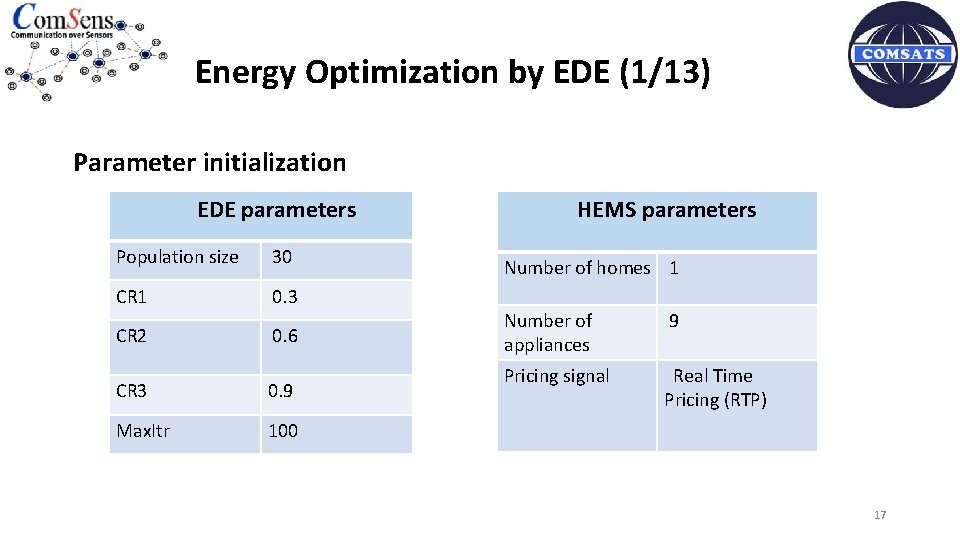
Energy Optimization by EDE (1/13) Parameter initialization EDE parameters Population size 30 CR 1 0. 3 CR 2 0. 6 CR 3 0. 9 Max. Itr 100 HEMS parameters Number of homes 1 Number of appliances 9 Pricing signal Real Time Pricing (RTP) 17

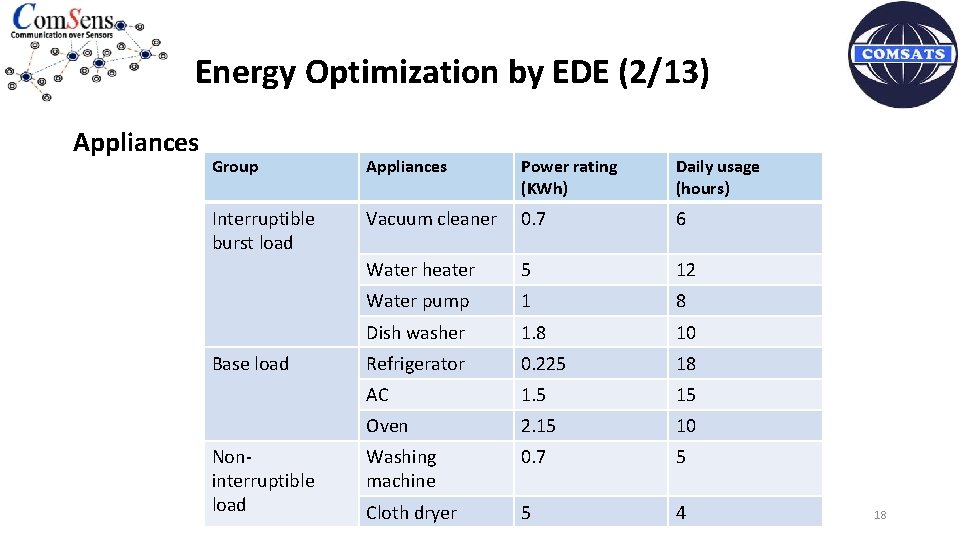
Energy Optimization by EDE (2/13) Appliances Group Appliances Power rating (KWh) Daily usage (hours) Interruptible burst load Vacuum cleaner 0. 7 6 Water heater 5 12 Water pump 1 8 Dish washer 1. 8 10 Refrigerator 0. 225 18 AC 1. 5 15 Oven 2. 15 10 Washing machine 0. 7 5 Cloth dryer 5 4 Base load Noninterruptible load 18

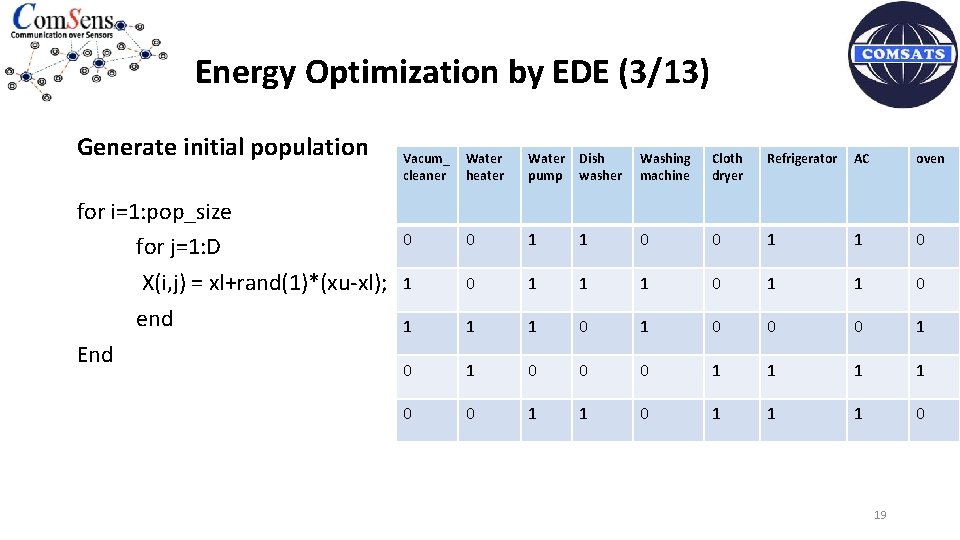
Energy Optimization by EDE (3/13) Generate initial population for i=1: pop_size for j=1: D X(i, j) = xl+rand(1)*(xu-xl); end End Vacum_ cleaner Water heater Water pump Dish washer Washing machine Cloth dryer Refrigerator AC oven 0 0 1 1 1 0 1 1 1 0 1 0 0 0 1 1 1 0 19

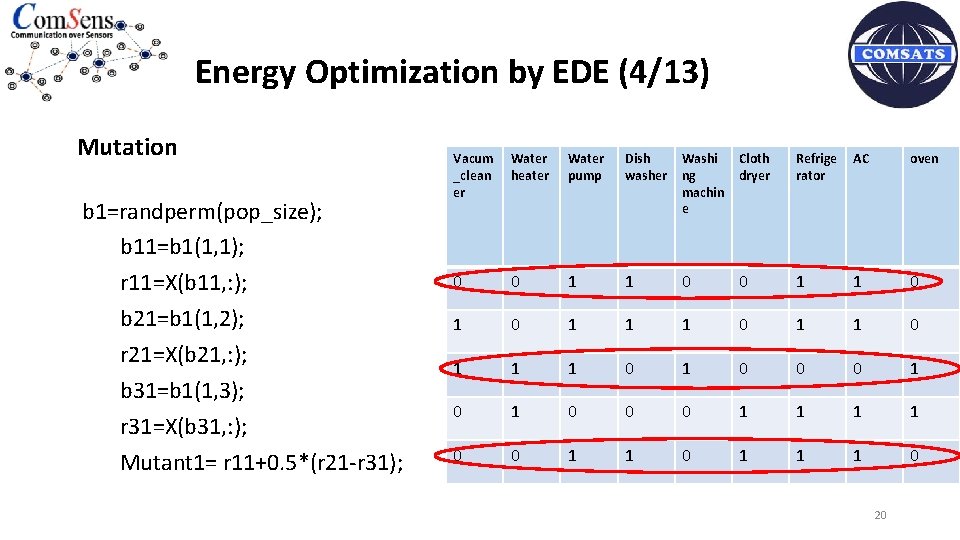
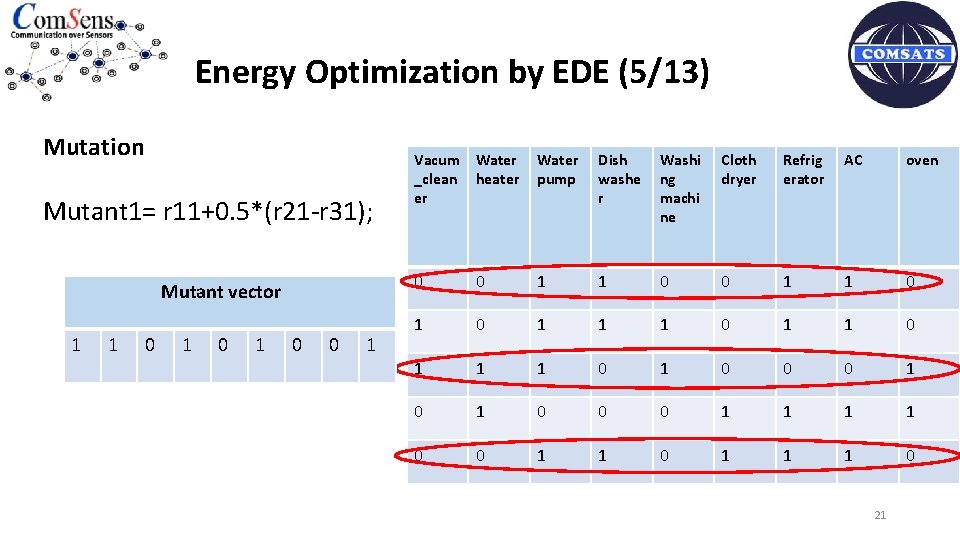
Energy Optimization by EDE (4/13) Mutation b 1=randperm(pop_size); b 11=b 1(1, 1); r 11=X(b 11, : ); b 21=b 1(1, 2); r 21=X(b 21, : ); b 31=b 1(1, 3); r 31=X(b 31, : ); Mutant 1= r 11+0. 5*(r 21 -r 31); Vacum _clean er Water heater Water pump Dish washer Washi ng machin e Cloth dryer Refrige rator AC oven 0 0 1 1 1 0 1 1 1 0 1 0 0 0 1 1 1 0 20

Energy Optimization by EDE (5/13) Mutation Mutant 1= r 11+0. 5*(r 21 -r 31); Mutant vector 1 1 0 1 0 0 1 Vacum Water _clean heater er Water pump Dish washe r Washi ng machi ne Cloth dryer Refrig erator AC oven 0 0 1 1 1 0 1 1 1 0 1 0 0 0 1 1 1 0 21

Energy Optimization by EDE (6/13) Crossover for i=1: D if rand(1)>=0. 3 Y 11(1, i)=r 11(1, D); else Y 11(1, i)=Mutant 1(1, D); end Target vector Mutant vector 0 0 1 1 0 1 0 0 1 First trial vector 1 0 0 1 0 1 1 22

Energy Optimization by EDE (7/13) Crossover for i=1: D if rand(1)>=0. 6 Y 21(1, i)=r 11(1, i); else Y 21(1, i)=Mutant 1(1, i); end Target vector Mutant vector 0 0 1 1 0 1 0 0 1 Second trial vector 0 1 1 1 0 0 1 23

Energy Optimization by EDE (8/13) Crossover for i=1: D if rand(1)>=0. 9 Y 31(1, i)=r 11(1, i); else Y 31(1, i)=Mutant 1(1, i); end Target vector Mutant vector 0 0 1 1 0 1 0 0 1 third trial vector 1 1 0 0 1 1 0 24

Energy Optimization by EDE (9/13) Crossover for i=1: D Y 41(1, i) = rand(1)*r 11(1, i); end Target vector Mutant vector 0 0 1 1 0 1 0 0 1 Fourth trial vector 0 for i=1: D Y 51(1, i) = rand(1)*Mutant 1(1, i)+(1 rand(1))*r 11(1, i); end 0 1 0 0 0 1 1 0 0 Fifth trial vector 1 0 0 1 1 0 25

Energy Optimization by EDE (10/13) Crossover F 11=Electricity_cost*Y 1_1'; F 21=Electricity_cost*Y 2_1'; F 31=Electricity_cost*Y 3_1'; F 41=Electricity_cost*Y 4_1'; F 51=Electricity_cost*Y 5_1'; F=[F 11 F 21 F 31 F 41 F 51 ]; Trial vectors 1 0 0 1 0 1 1 14. 5 0 1 1 1 0 1 0 0 1 1 0 16 0 1 0 0 0 1 1 0 17. 5 0 0 1 1 0 0 19 if min(F)==F 11 0 T=Y 1_1; 1 elseif min(F)==F 21 T=Y 2_1; elseif min(F)==F 31 T=Y 3_1; elseif min(F)==F 41 T=Y 4_1; else min(F)==F 51 T=Y 5_1; end Cost Final trial vector 0 1 1 1 0 0 1 26

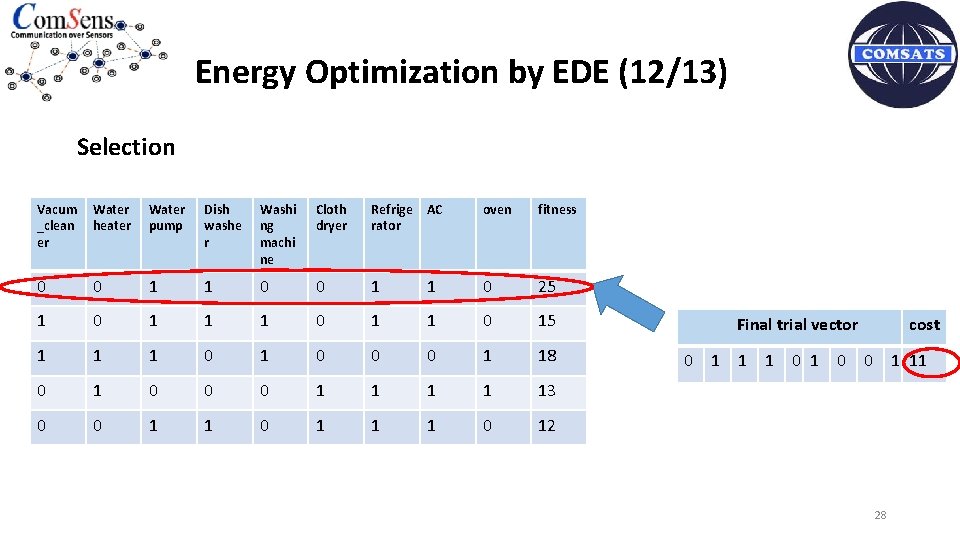
Energy Optimization by EDE (11/13) Selection T 11=Electricity_cost*T'; T 12=Electricity_cost*r 11_1'; if T 12 < T 11 X(b 11, : )=r 11_1; else X(b 11, : )=T; end Target vector 0 0 1 1 Cost 0 0 1 1 0 Final trial vector 0 1 1 1 0 25 Cost 1 0 0 1 11 27

Energy Optimization by EDE (12/13) Selection Vacum _clean er Water heater Water pump Dish washe r Washi ng machi ne Cloth dryer Refrige rator AC oven fitness 0 0 1 1 0 25 1 0 15 1 1 1 0 0 0 1 18 0 1 0 0 0 1 1 13 0 0 1 1 1 0 12 Final trial vector cost 0 1 1 1 0 0 1 11 28

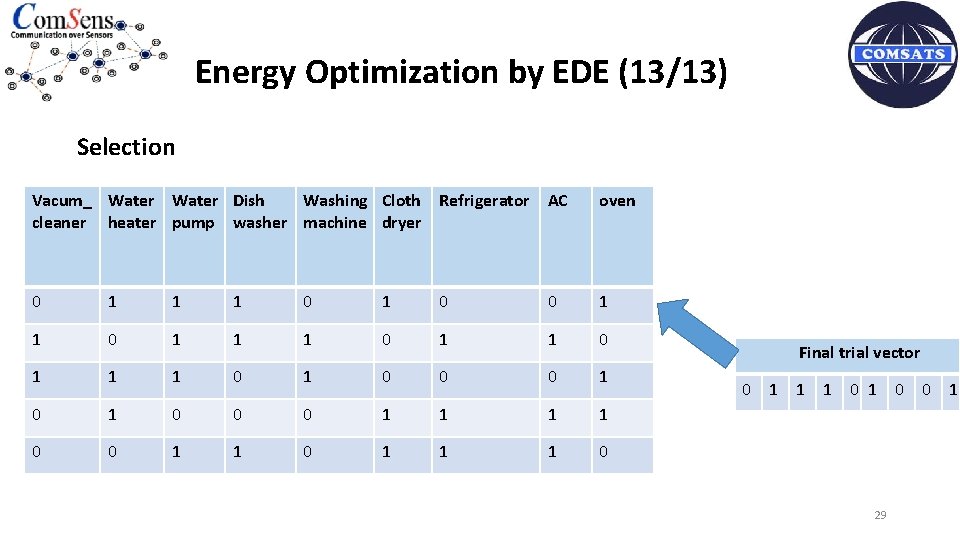
Energy Optimization by EDE (13/13) Selection Vacum_ Water Dish Washing Cloth Refrigerator AC cleaner heater pump washer machine dryer oven 0 1 1 1 0 0 1 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 Final trial vector 0 1 1 1 0 0 1 29

30

Thank You Any Question 31