Differential Equations Slope Fields 1 Slope Fields Recall





- Slides: 9

Differential Equations: Slope Fields 1

Slope Fields � Recall that indefinite integration, or antidifferentiation, is the process of reverting a function from its derivative. In other words, if we have a derivative, the antiderivative allows us to regain the function before it was differentiated – except for the constant , of course. � If we are given the derivative dy/dx = f ‘ (x) and we solve for y (or f (x)), we are said to have found the general solution of a differential equation. � For example: Let And we can easily solve this: This is the general solution:

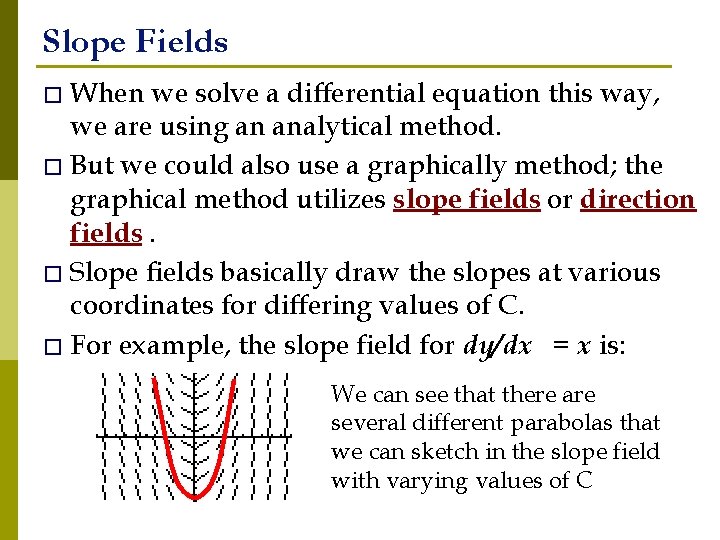
Slope Fields � When we solve a differential equation this way, we are using an analytical method. � But we could also use a graphically method; the graphical method utilizes slope fields or direction fields. � Slope fields basically draw the slopes at various coordinates for differing values of C. � For example, the slope field for dy/dx = x is: We can see that there are several different parabolas that we can sketch in the slope field with varying values of C

Slope Fields � Let’s examine how we create a slope field. � For example, create the slope field for the differential equation (DE): Since dy/dx gives us the slope at any point, we just need to input the coordinate: At (-2, 2), dy/dx = -2/2 = -1 At (-2, 1), dy/dx = -2/1 = -2 At (-2, 0), dy/dx = -2/0 = undefined And so on…. This gives us an outline of a hyperbola

Slope Fields � Let’s examine how we create a slope field. � For example, create the slope field for the differential equation (DE): Of course, we can also solve this differential equation analytically:

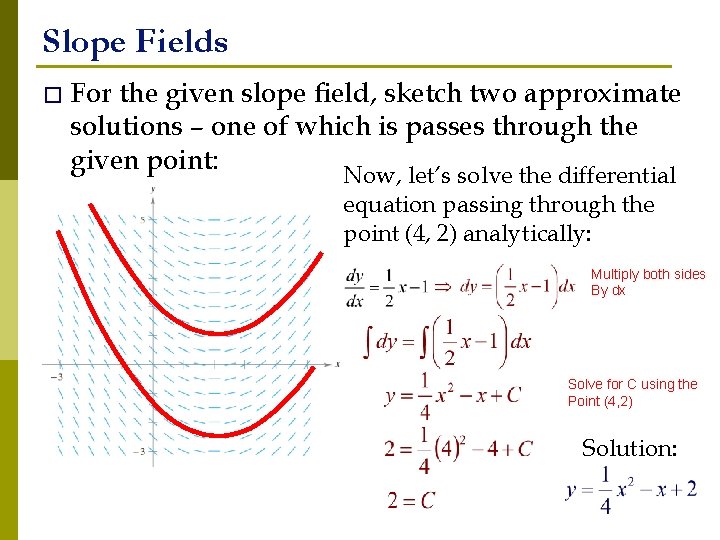
Slope Fields � For the given slope field, sketch two approximate solutions – one of which is passes through the given point: Now, let’s solve the differential equation passing through the point (4, 2) analytically: Multiply both sides By dx Solve for C using the Point (4, 2) Solution:

Slope Fields Match the correct DE with its graph: A B H 1. _____ In order to determine a slope field from a differential equation, we should consider the following: F 2. _____ i) If isoclines (points with the same slope) are along horizontal lines, then DE depends only on y ii) Do you know a slope at a particular point? iii) If we have the same slope along vertical lines, then DE depends only on x iv) Is the slope field sinusoidal? v) What x and y values make the slope 0, 1, or undefined? vi) dy/dx = a(x ± y) has similar slopes along a diagonal. vii) Can you solve the separable DE? 3. _____ D C 4. _____ A 5. _____ E F G 6. _____ E 7. _____ B 8. _____ G H

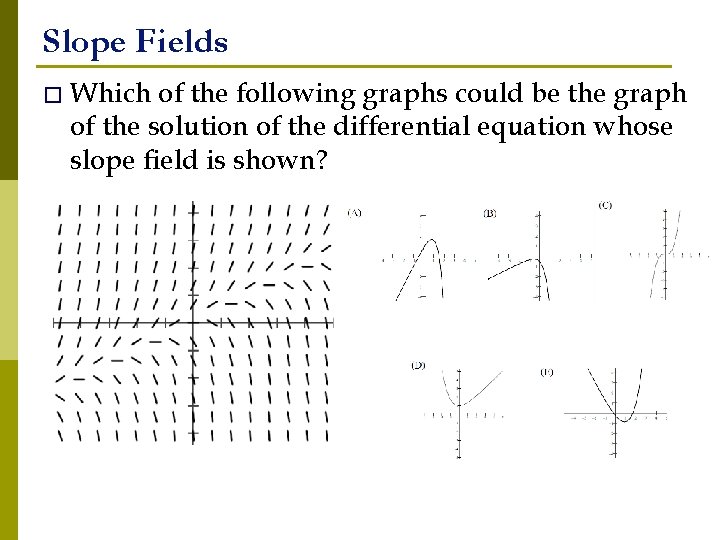
Slope Fields � Which of the following graphs could be the graph of the solution of the differential equation whose slope field is shown?

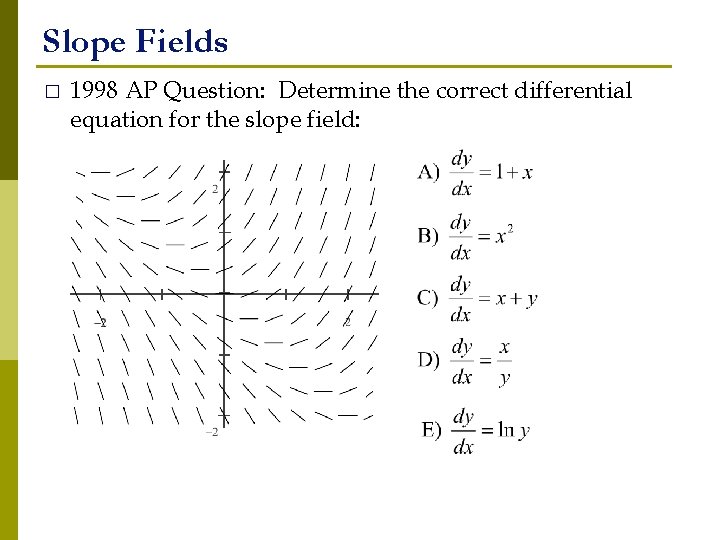
Slope Fields � 1998 AP Question: Determine the correct differential equation for the slope field: