Differential Equations Lecture 7 System of Linear Differential

Differential Equations Lecture 7 System of Linear Differential Equations fall semester Instructor: A. S. Brwa / MSc. In Structural Engineering College of Engineering / Ishik University

Ishik University Systems of First Order Linear ODE In this lecture you will learn how to solve systems of simultaneous homogeneous first order linear differential equations. The solutions of such systems require good knowledge of linear algebra. Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 2

Ishik University Systems of First Order Linear ODE A system of n linear first order differential equations in n unknowns (an n × n system of linear equations) has the general form: Where the coefficients aij’s, and gi’s are arbitrary functions of t. If every term gi is constant zero, then the system is said to be homogeneous. Otherwise, it is a nonhomogeneous system if even one of the g’s is nonzero. Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 3

Ishik University Systems of First Order Linear ODE The system (*) is most often given in a shorthand format as a matrixvector equation, in the form: Where the matrix of coefficients, A, is called the coefficient matrix of the system. Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 4

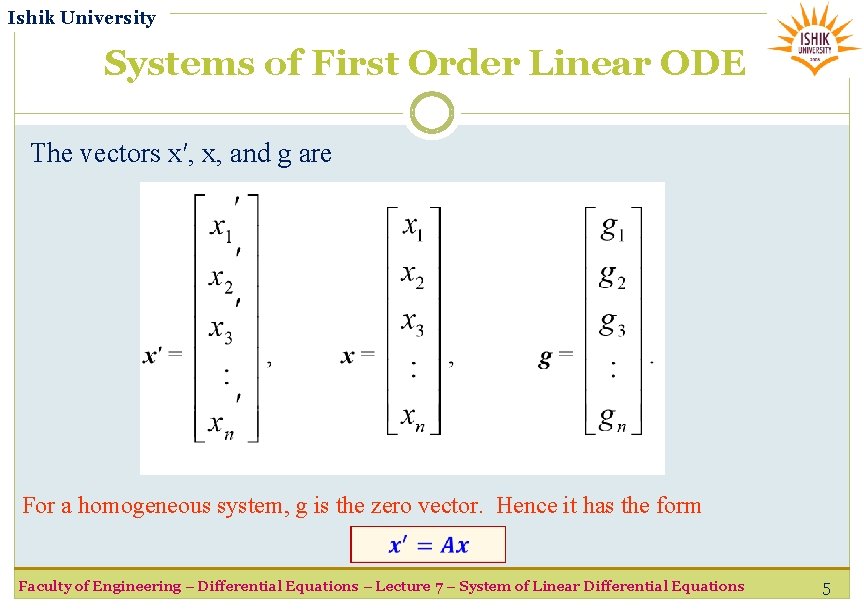
Ishik University Systems of First Order Linear ODE The vectors x′, x, and g are For a homogeneous system, g is the zero vector. Hence it has the form Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 5

Ishik University Systems of First Order Linear ODE Fact: Every n-th order linear equation is equivalent to a system of n first order linear equations. (This relation is not one-to-one. There are multiple systems thus associated with each linear equation, for n > 1. ) Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 6

Ishik University Systems of First Order Linear ODE � Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 7

Ishik University Systems of First Order Linear ODE � Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 8

Ishik University Systems of First Order Linear ODE � Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 9

Ishik University Systems of First Order Linear ODE � Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 10

Ishik University Systems of First Order Linear ODE � Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 11

Ishik University Systems of First Order Linear ODE Example-3: Convert the following linear differential equations into a system of first order equations Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 12

Ishik University Systems of First Order Linear ODE Example-3: Convert the following linear differential equations into a system of first order equations Solution: Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 13

Ishik University Systems of First Order Linear ODE Example-3: Convert the following linear differential equations into a system of first order equations Solution: Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 14

Ishik University Systems of First Order Linear ODE Example-3: Convert the following linear differential equations into a system of first order equations Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 15

Ishik University Systems of First Order Linear ODE Example-3: Convert the following linear differential equations into a system of first order equations Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 16

Ishik University Systems of First Order Linear ODE Example-3: Convert the following linear differential equations into a system of first order equations Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 17

Ishik University Systems of First Order Linear ODE Example-4: Rewrite the system you found in (a) Example 3. 1, (b) Example 3. 2, (c) Example 3. 3, into a matrix-vector equation. Answer: Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 18

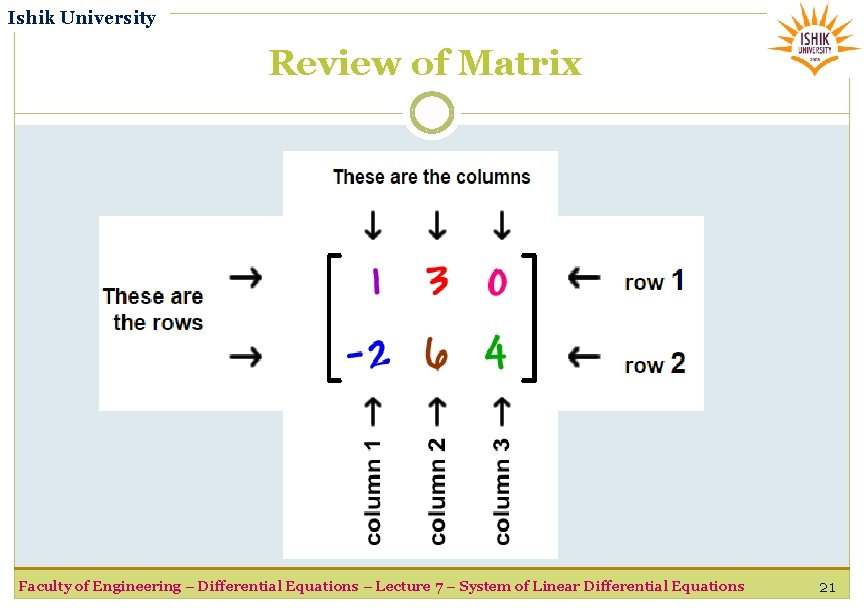
Ishik University Review of Matrix Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 19

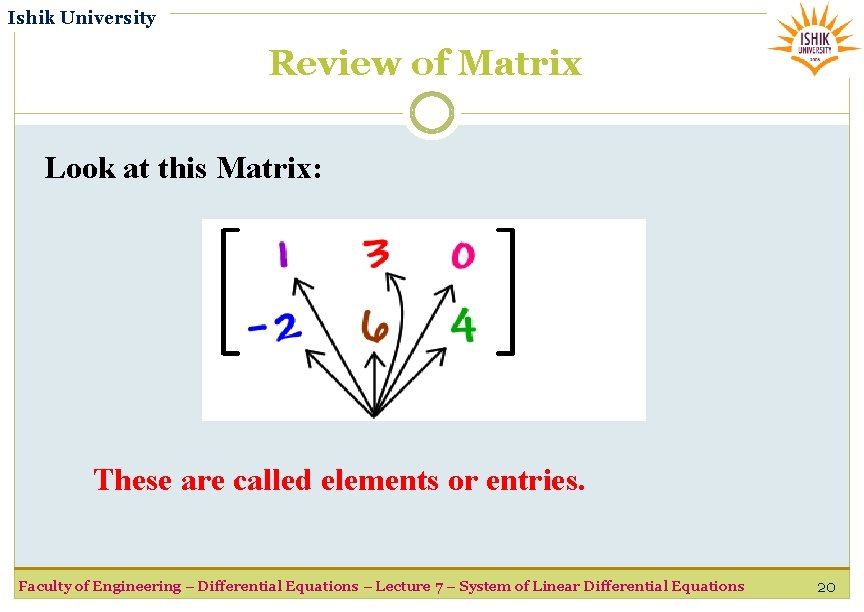
Ishik University Review of Matrix Look at this Matrix: These are called elements or entries. Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 20

Ishik University Review of Matrix Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 21

Ishik University Review of Matrix What's the size of this matrix? 3 rows and 2 columns. This is a 3 by 2 matrix (3 x 2). Note: A 2 x 3 matrix and a 3 x 2 matrix are definitely different sizes! Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 22

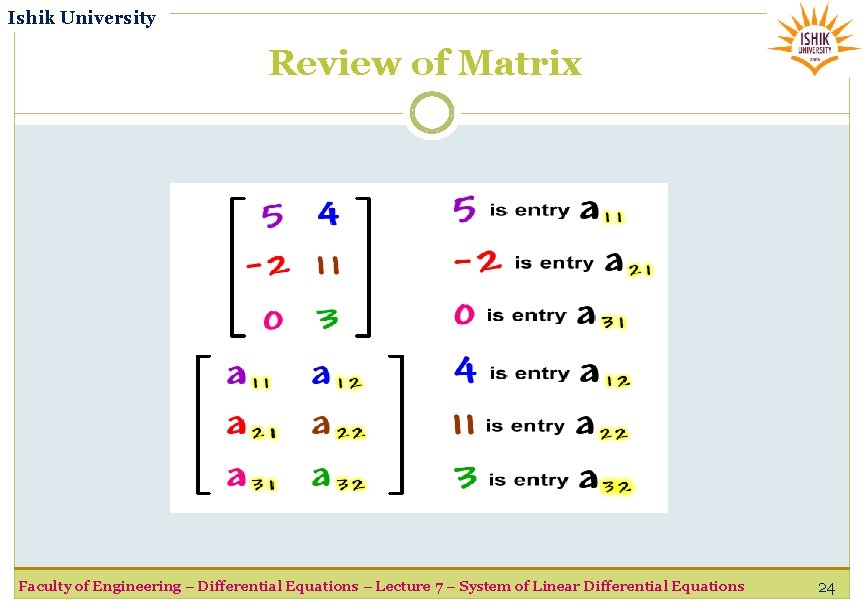
Ishik University Review of Matrix Sometimes, we'll need to refer to a specific entry, so we have a special "tagging" system. It's based on rows and columns: This element is located in the column row and in the Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 23

Ishik University Review of Matrix Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 24

Ishik University Review of Matrix A vector: is a special type of matrix that has only one row (called a row vector) or one column (called a column vector). Below, a is a column vector while b is a row vector. Vectors are denoted by bold, lower case letters (e. g. , x). Row vector Column vector A scalar: is a matrix with only one row and one column. It is customary to denote scalars by italicized, lower case letters (e. g. , x) Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 25

Ishik University Review of Matrix Square Matrices: A square matrix A has the same number of rows and columns. That is, A is n x n. In this case, A is said to have order n. Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 26

Ishik University Review of Matrix The Zero Matrix: The zero matrix is defined to be 0 = (0), whose dimensions depend on the context. For example, Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 27

Ishik University Review of Matrix Identity matrix: is a diagonal matrix with 1’s and only 1’s on the diagonal and zeros everywhere else. The identity matrix is almost always denoted as I. Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 28

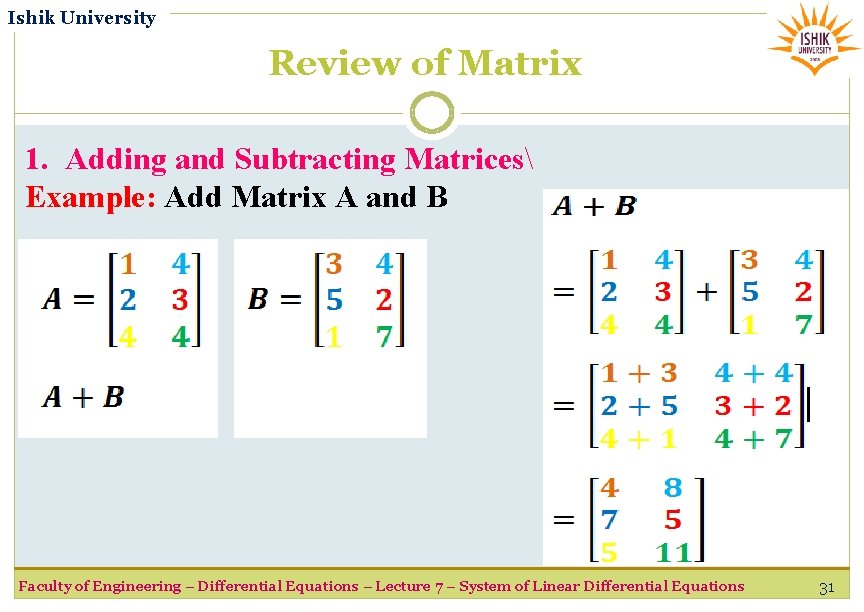
Ishik University Review of Matrix 1. Adding and Subtracting Matrices Adding and subtracting matrix is really easy, but THE SIZES MUST BE THE SAME! Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 29

Ishik University Review of Matrix 1. Adding and Subtracting Matrices Adding and subtracting matrix is really easy, but THE SIZES MUST BE THE SAME! Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 30

Ishik University Review of Matrix 1. Adding and Subtracting Matrices Example: Add Matrix A and B Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 31

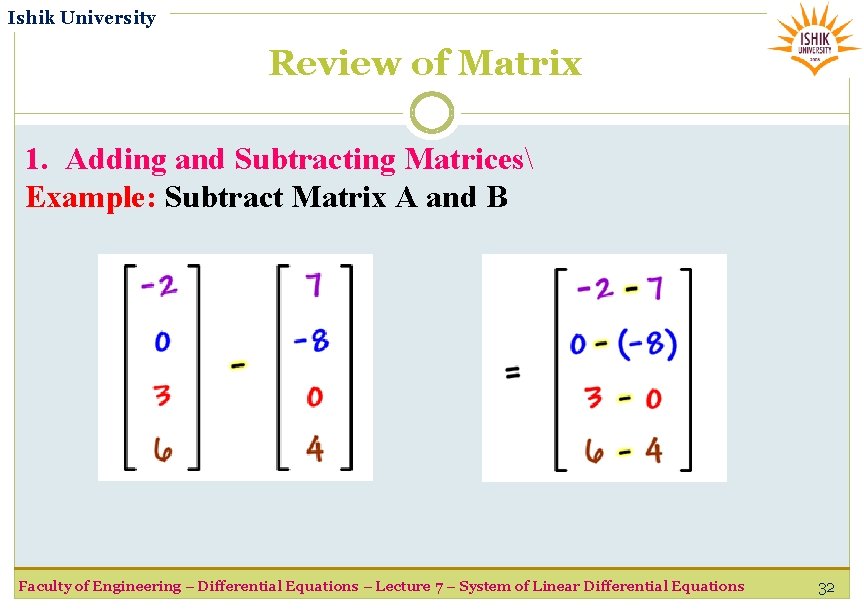
Ishik University Review of Matrix 1. Adding and Subtracting Matrices Example: Subtract Matrix A and B Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 32

Ishik University Review of Matrix Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 33

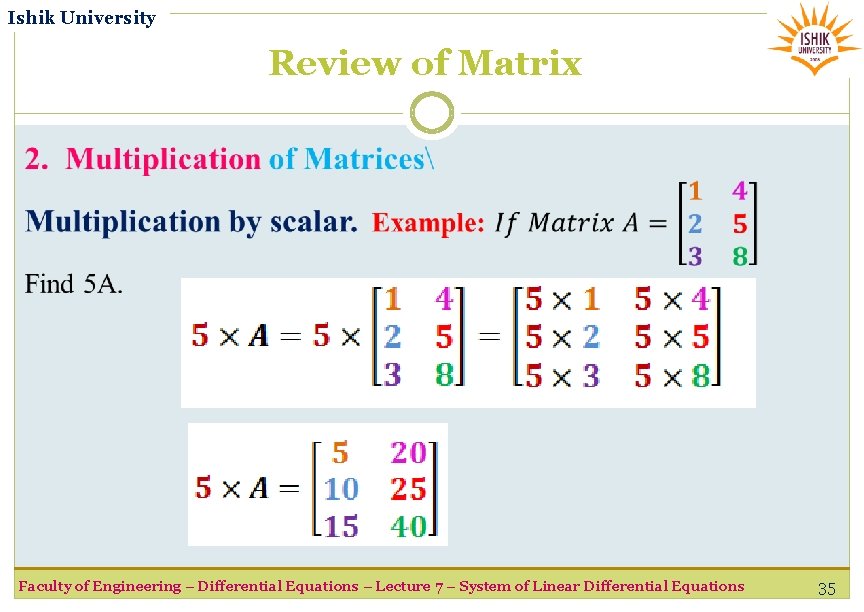
Ishik University Review of Matrix 2. Multiplication of Matrices Multiplication by scalar. Example: If Matrix Find 2 A. . . (2 times A) Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 34

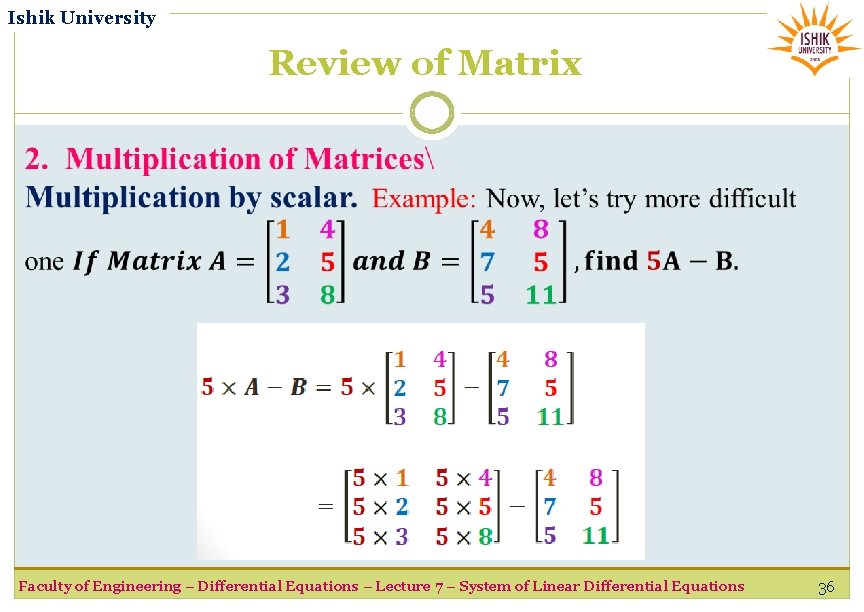
Ishik University Review of Matrix Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 35

Ishik University Review of Matrix Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 36

Ishik University Review of Matrix Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 37

Ishik University Review of Matrix 2. Multiplication of Matrices Multiplication of two matrices. To multiply two matrices together is a bit more difficult. First of all, the size of the two matrices you are multiplying is super important! If the size of matrix A is 3 x 4 and the size of matrix B is 4 x 1 And the answer will be a 3 x 1 matrix Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 38

Ishik University Review of Matrix Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 39

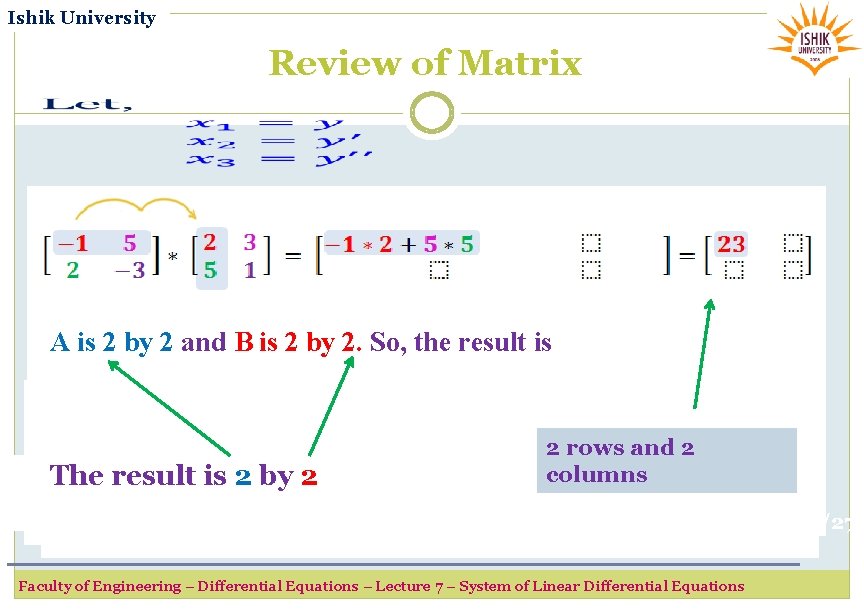
Ishik University Review of Matrix A is 2 by 2 and B is 2 by 2. So, the result is The result is 2 by 2 40/27 Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations

Ishik University Review of Matrix A is 2 by 2 and B is 2 by 2. So, the result is The result is 2 by 2 2 rows and 2 columns 41/27 Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations

Ishik University Review of Matrix Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 42

Ishik University Review of Matrix 43/27 Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations

Ishik University Review of Matrix 44/27 Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations

Ishik University Review of Matrix 3. Inverse matrix (of a square matrix) Given an n × n square matrix A, if there exists a matrix B (necessarily of the same size) such that Faculty of Engineering – Differential Equations – Lecture 7 – System of Linear Differential Equations 45