Differential Cryptanalysis quite similar to linear cryptanalysis exploits

Differential Cryptanalysis - quite similar to linear cryptanalysis - exploits the relationship between the difference of two inputs and the difference of the corresponding two outputs. - the difference MZ of two strings of bits Z′ and Z′′ is the bitwise XOR of the strings, i. e, MZ = Z′ © Z′′ - why look at the difference? because in an SPN, the key does not influence the value of the difference!

Differential Cryptanalysis In a perfectly randomized cipher, the probability of a given output difference MY, given an input difference MX, is (½)m, where m is the number of bits. The pair (MX, MY) is a differential. We will look for cases where this probability is much larger than (½)m. We will look at pairs of plaintexts that have a certain input difference. This is why differential cryptanalysis is a chosen-plaintext attack. As in the case of linear cryptanalysis, we will first look at the S-boxes.

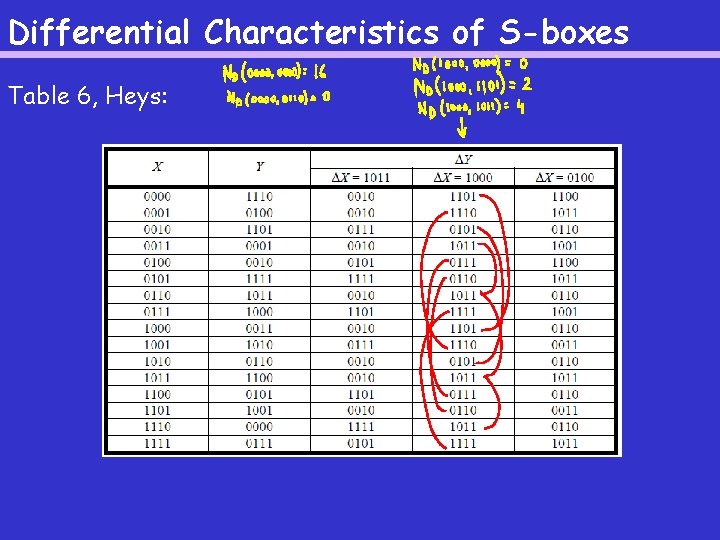
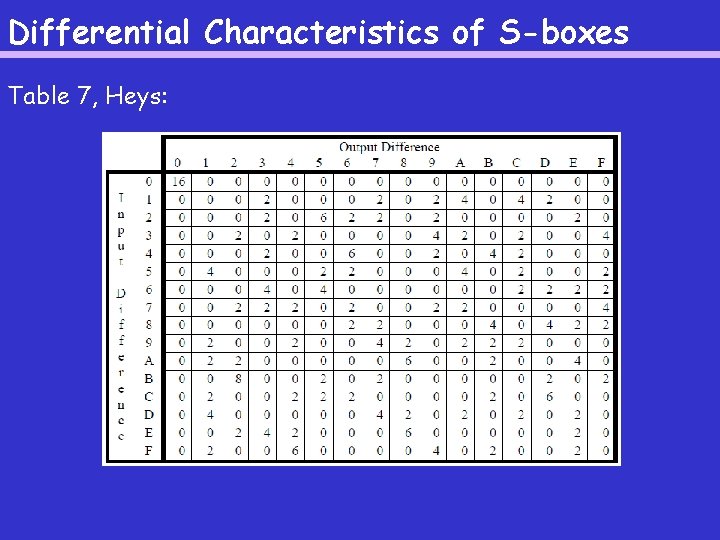
Differential Characteristics of S-boxes The S-box from the linear cryptanalysis slides (πS): 0 1 2 3 4 5 6 7 8 9 A B C D E F E 4 D 1 2 F B 8 3 A 6 C 5 9 0 7 For MX an input difference and MY an output difference, we will compute ND(MX, MY): the number of pairs with input difference equal to MX and output difference equal to MY. For example, ND(1011, 0010) = 8 (see Table 6). You can find all values in Table 7. In an ideal S-box, ND(MX, MY) = 1. Such an S-box is not mathematically possible.

Differential Characteristics of S-boxes Table 6, Heys:

Differential Characteristics of S-boxes Table 7, Heys:

Propagation Ratio From ND(MX, MY) we can compute the propagation ratio: Rp(MX, MY) = ND(MX, MY) / 2 m Notice: Rp(MX, MY) = Pr[ output-difference = MY | input-difference = MX ] For example, in our S-box, RP(1011, 0010) = 1/2.

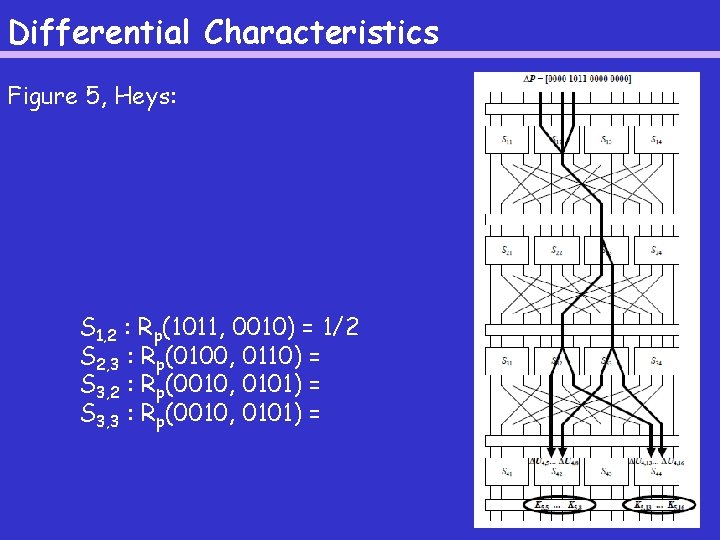
Differential Characteristics We will combine the differential characteristics of the -boxes to obtain a differential characteristic of the whole cipher. S We will look at the same example SPN as for linear cryptanalysis (Figure 1). We will look at the following S-boxes and difference pairs (Figure 5). S 1, 2 : Rp(1011, 0010) = 1/2 S 2, 3 : Rp(0100, 0110) = S 3, 2 : Rp(0010, 0101) = S 3, 3 : Rp(0010, 0101) = We assume that these propagation ratios are independent. This assumption works well in practice.

Differential Characteristics Figure 5, Heys: S 1, 2 : Rp(1011, 0010) = 1/2 S 2, 3 : Rp(0100, 0110) = S 3, 2 : Rp(0010, 0101) = S 3, 3 : Rp(0010, 0101) =

Differential Characteristics All other S-boxes will have all 0 s as input difference, and thus all 0 s as output difference. Combining the S-boxes, we obtain the following propagation ratio for the first three rounds of the SPN: Rp(0000 1011 0000, 0000 0101) = 1/2(3/8)3 = 27/1024. This implies that the propagation ratio “from the plaintext to U 4” is given by Rp(0000 1011 0000, 0000 0101) = 27/1024.

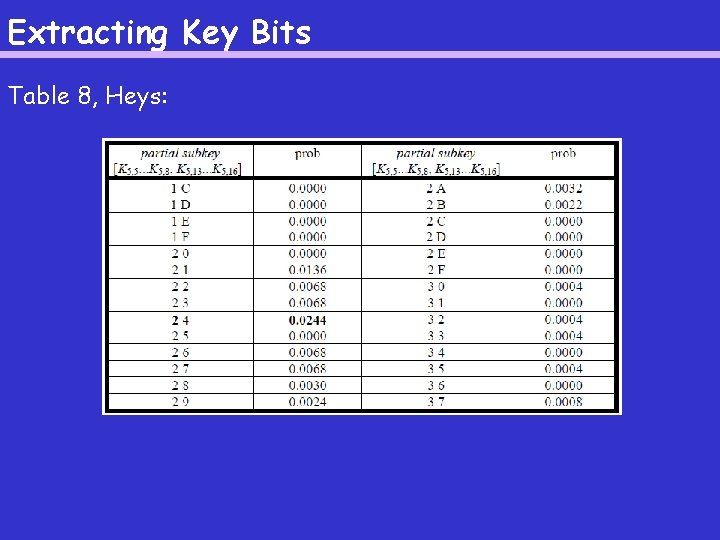
Extracting Key Bits We will use the above propagation ratio to determine part of subkey K 5. Suppose we have a large number of plaintext pairs (X′, X′′) such that MX = X′ © X′′ = 0000 1011 0000. Let (Y′, Y′′) be the corresponding ciphertexts. We will partially decrypt each pair of ciphertexts and see if the resulting decryptions have difference equal to 0000 0101. As in the linear case, we have to go through all (2 8) possibilities for the subkey bits K 5, 5, K 5, 6, K 5, 7, K 5, 8, K 5, 13, K 5, 14, K 5, 15, K 5, 16.

Extracting Key Bits For each candidate subkey, partially decrypt each pair of ciphertexts (by XOR-ing with the candidate subkey and running the data backwards through the S-boxes), and compute the probability that the difference of the decryptions = 0000 0101. The idea is that this fraction is largest for the correct 8 key bits. See Table 8. Note: Often, it is not necessary to partially decrypt Y′ and Y′′ to see that they don’t fulfill the required differential. Why not? This observation is useful in speeding up the algorithm.

Extracting Key Bits Table 8, Heys:

Extracting Key Bits How many plaintext pairs do we need ? As a rule-of-thumb, if the propagation ratio is equal to ², the number of pairs of plaintexts with the chosen difference value and corresponding ciphertexts needed is c²− 1 for some “small” constant c.

Advanced Issues To strengthen the attacks you could • Combine different linear approximations for the cipher. • Combine differential characteristics for the cipher. • Combine linear and differential cryptanalysis. • Look at something other than XOR in differential cryptanalysis. • … We have not discussed how to determine the best linear and differential attack.