Differentiability for Functions of Two or more Variables

Differentiability for Functions of Two (or more!) Variables Local Linearity

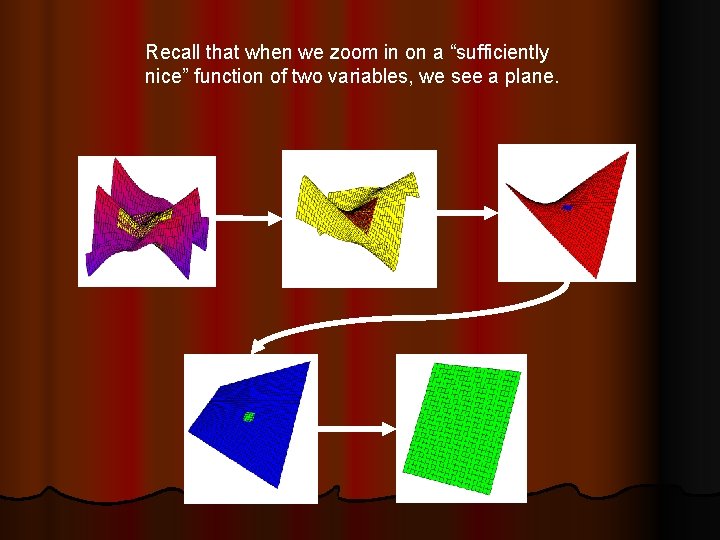
Recall that when we zoom in on a “sufficiently nice” function of two variables, we see a plane.

Differentiability: A precise definition A function f(x, y) is said to be differentiable at the point (a, b) provided that there exist real numbers m and n and a function E(x, y) such that for all x and y and

What is meant by “sufficiently nice”? Suppose we zoom in on the function z=f(x, y) centering our zoom on the point (a, b) and we see a plane. What can we say about the plane? l The partial derivatives for the plane at the point must be the same as the partial derivatives for the function--In particular, the partial derivatives must all exist! l The equation for the tangent plane is

Partial Derivatives Exist Suppose we have a function Notice several things: • The function is not continuous at x=0. • The function is not locally planar at x=0. • Both partial derivatives exist at x=0.

Directional Derivatives? It’s not even good enough for all of the directional derivatives to exist! Just take a function that is a bunch of straight lines through the origin with random slopes. (One for each direction in the plane. )

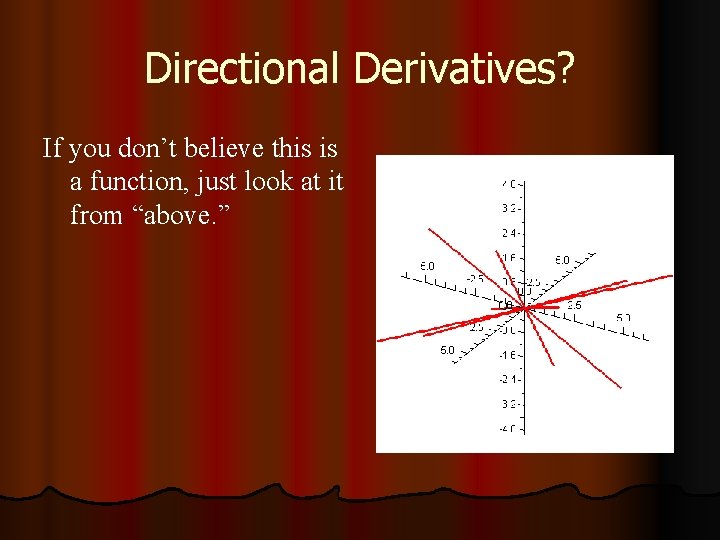
Directional Derivatives? If you don’t believe this is a function, just look at it from “above. ”

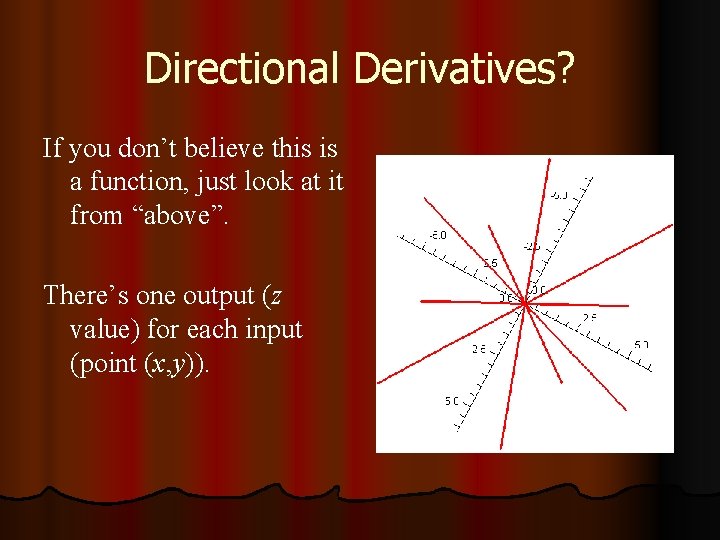
Directional Derivatives? If you don’t believe this is a function, just look at it from “above”. There’s one output (z value) for each input (point (x, y)).

Differentiability The function z = f(x, y) is differentiable (locally planar) at the point (a, b) if and only if the partial derivatives of f exist and are continuous in a small disk centered at (a, b).