Didactical Triangle Ididactical System Teaching Creating best possible
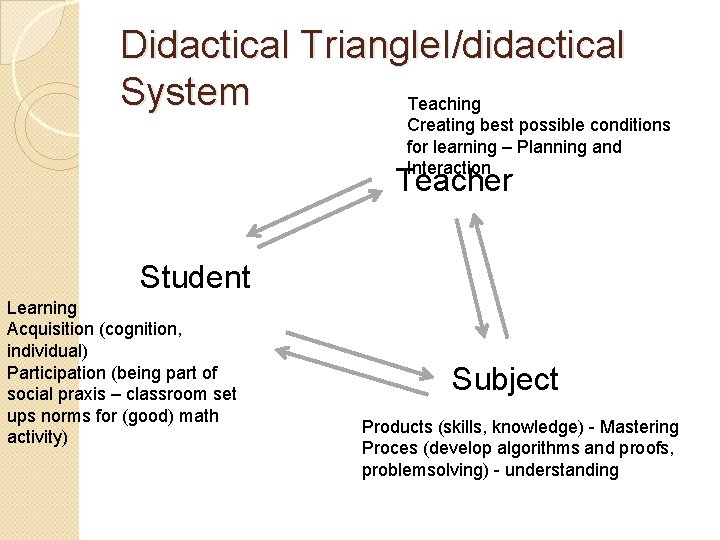
Didactical Triangle. I/didactical System Teaching Creating best possible conditions for learning – Planning and Interaction Teacher Student Learning Acquisition (cognition, individual) Participation (being part of social praxis – classroom set ups norms for (good) math activity) Subject Products (skills, knowledge) - Mastering Proces (develop algorithms and proofs, problemsolving) - understanding

The Theory of Didactical Situations - TDS Theory ? Knowledge

TDS – Guy Brousseau TDS is in this context presented more like a didactic approach than a theory

TDS – Guy Brousseau Knowledge is transformed/exchanged between 3 main groups of actors: Researchers Teachers Students For each group there is a distinction between two forms of subject knowledge – depending on the actor: • Personal knowledge (Implicit, contextual, explicit) • Shared/common/official knowledge (explicit, e. g. textbooks, articles) Learning means two processes: Shared knowledge Personal knowledge Shared

TDS – Guy Brousseau: • A teacher is normally asking questions of which he/she knows the answer – an artificial situation • Outside teaching-learning situations you ask questions in order to get an answer to what you did not know • Brousseau wants to overcome this paradox

TDS – Guy Brousseau: • Traditional teaching in Math and Science tend are in practice based on transfer • Student do not learn mathematics but they learn to decode teacher’s expectations • So students learn a certain perception of what mathematics is or what it is about
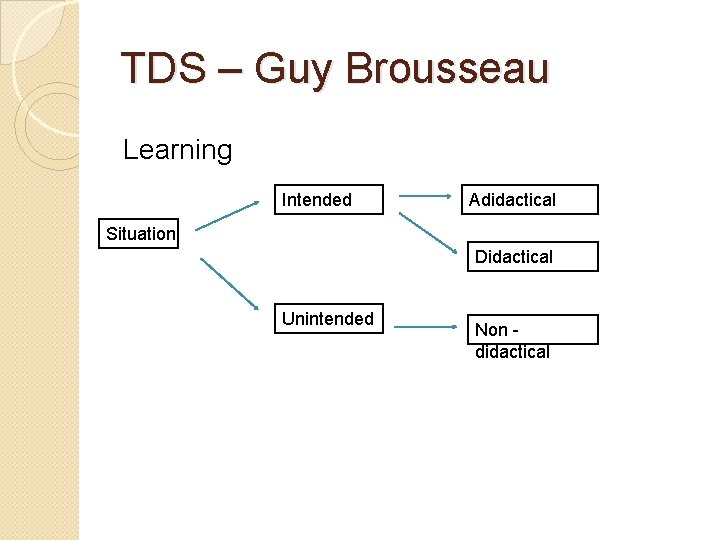
TDS – Guy Brousseau Learning Intended Adidactical Situation Didactical Unintended Non didactical
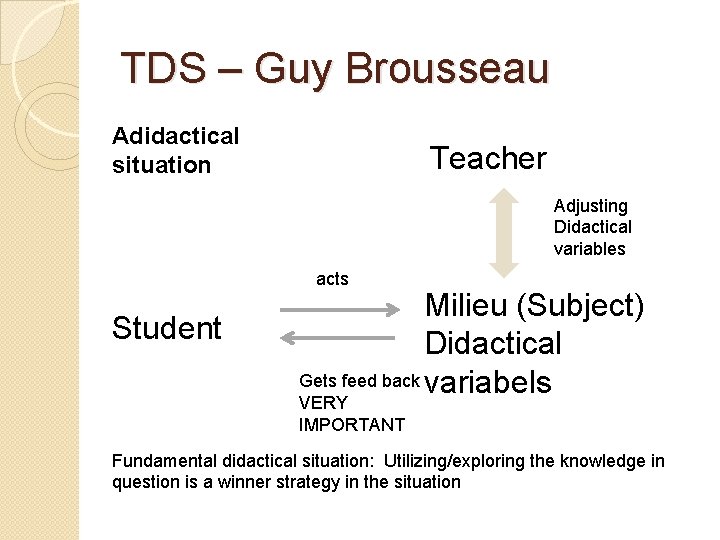
TDS – Guy Brousseau Adidactical situation Teacher Adjusting Didactical variables acts Student Milieu (Subject) Didactical Gets feed back variabels VERY IMPORTANT Fundamental didactical situation: Utilizing/exploring the knowledge in question is a winner strategy in the situation

TDS – Guy Brousseau Characteristics of a fundamental didactical situation: • Sufficient pre knowledge in order to understand the challenge and be able to suggest answers • Feed back incorporated so students’ strategies are validated without the teachers interference • Sufficient uncertainty (complexity) in order to avoid obvious beforehand judgements of suggested strategy • Possibility for trial and error – many attempts • The aimed knowledge must be a condition for reaching the new strategy

TDS – Guy Brousseau The puzzle example
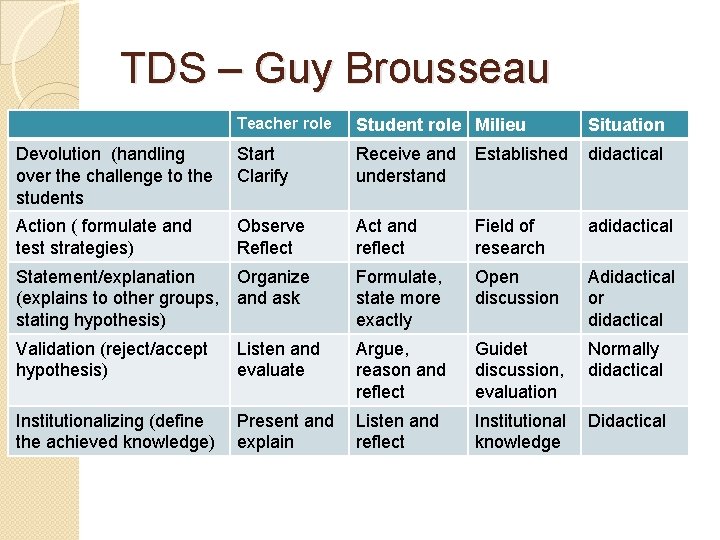
TDS – Guy Brousseau Teacher role Student role Milieu Situation Devolution (handling over the challenge to the students Start Clarify Receive and understand Established didactical Action ( formulate and test strategies) Observe Reflect Act and reflect Field of research adidactical Statement/explanation (explains to other groups, stating hypothesis) Organize and ask Formulate, state more exactly Open discussion Adidactical or didactical Validation (reject/accept hypothesis) Listen and evaluate Argue, reason and reflect Guidet discussion, evaluation Normally didactical Institutionalizing (define the achieved knowledge) Present and explain Listen and reflect Institutional knowledge Didactical

TDS – Guy Brousseau Do we know the Phases? Construct a didactical situation – state exactly the topic and the didactical variables.

TDS – Guy Brousseau Example: logistic growth

RME - Freudenthal Realistic Mathematics Education. Basic idea: Mathematics must be considered a special approach to solve problems related to the world outside

RME - Freudenthal Methods and concepts are there but the student’s understanding is to be developed through more informal work with problems related to the world outside Guided reinvention: students are supposed to reason, develop, generalize and systematize their informal work

RME - Freudenthal ”The learner should reinvent mathematising rather than mathematics, abtracting rather than abstractions, schematising rather than schemes, algorithmising rather than algorithms, verbalising rather than language” (Freudenthal)

RME - Freudenthal Model concept – emergent models • activity based on the given context • referential level – a model of the given context is developed – reflect on the context • general level – the model becomes a model for situations in outside world – it gets it’s own life - reflect on the model – thinking with • formal level – pure mathematical investigations can be possible – the significance of parameters…Thinking

RME - Freudenthal Example: Taxi functions

RME - Freudenthal ”By describing their own process students can use their reflections to develop flexible prototypes of experiences that can be drawn on in future problem solving” (Lesh & Zawojewski) ”A fresh view of problem solving needs to view the learning of mathematics and problem solving as integrated, as largely based on modelling activity, and as a construct that is itself continually in need of development” (Lesh & Zawojewski)
- Slides: 19