DIAMETER P Distance across the circle through its







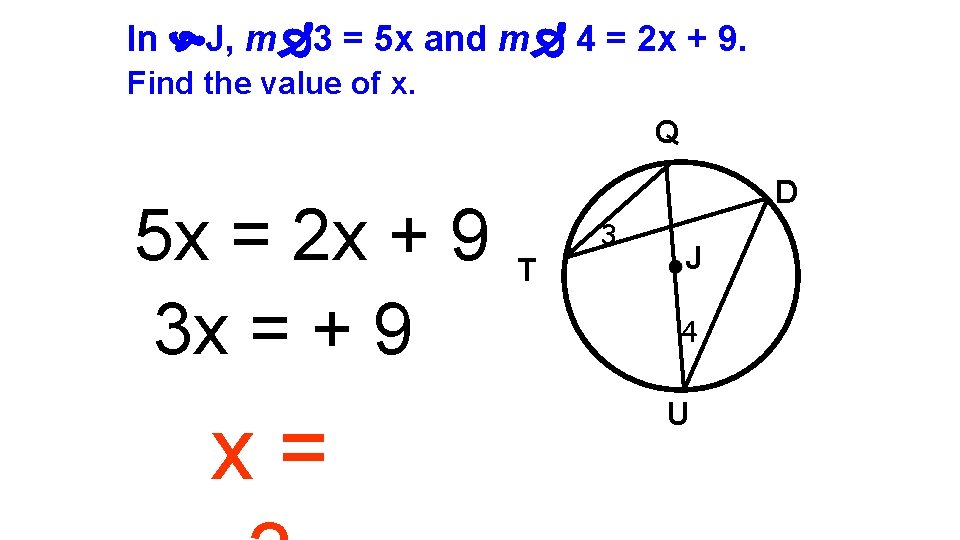

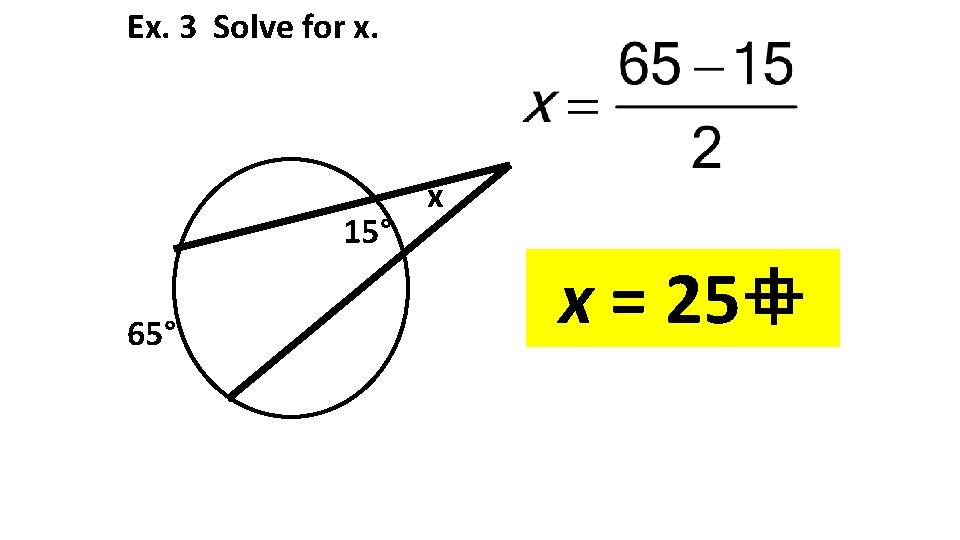






- Slides: 49

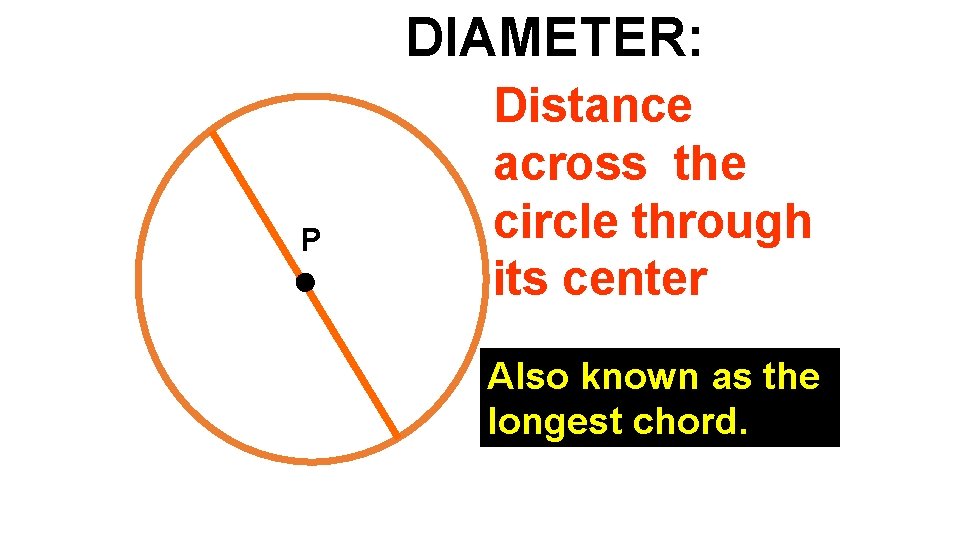
DIAMETER: P Distance across the circle through its center Also known as the longest chord.

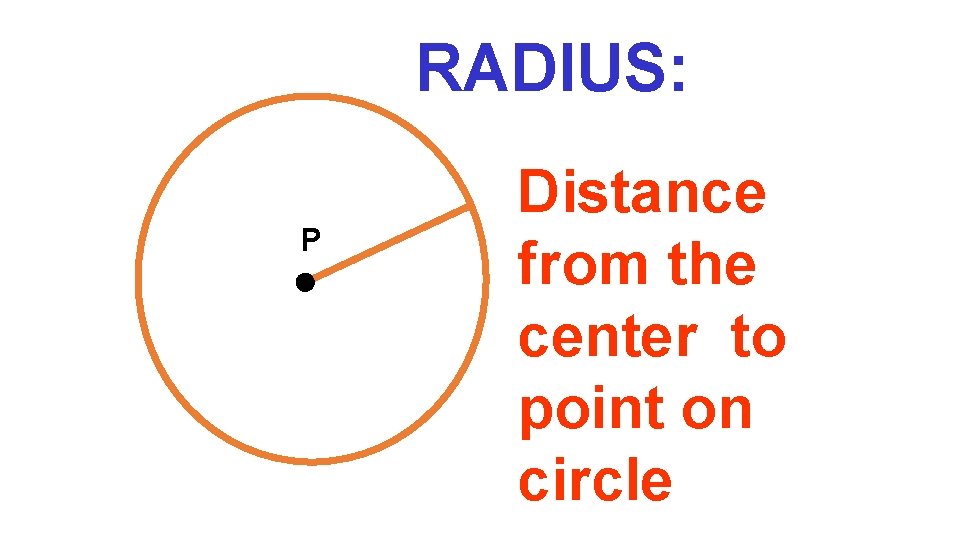
RADIUS: P Distance from the center to point on circle

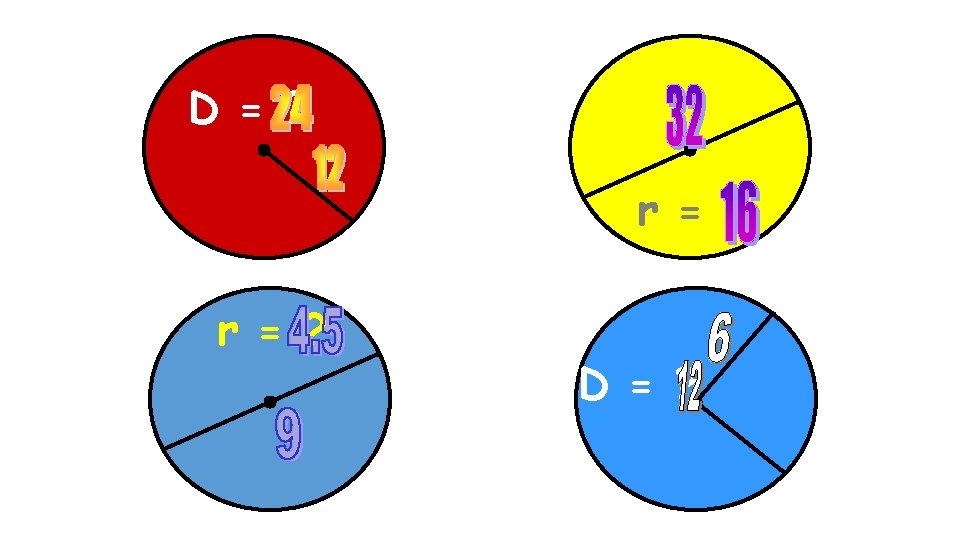
Formula Radius = ½ diameter or Diameter = 2 r


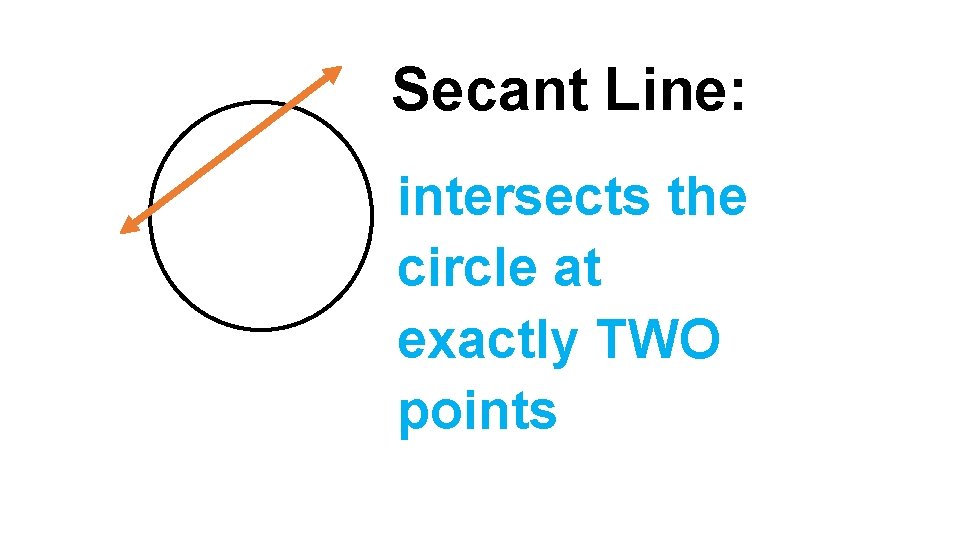
Secant Line: intersects the circle at exactly TWO points

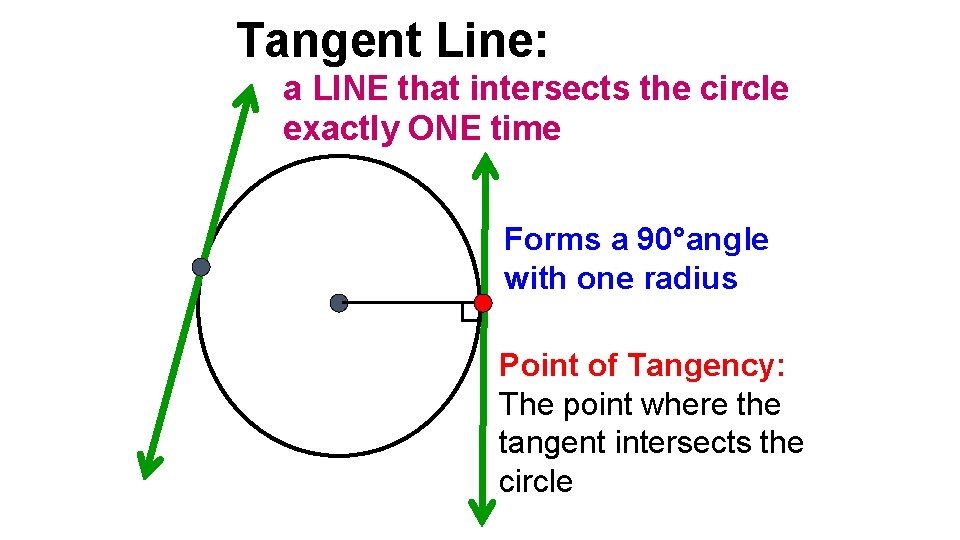
Tangent Line: a LINE that intersects the circle exactly ONE time Forms a 90°angle with one radius Point of Tangency: The point where the tangent intersects the circle

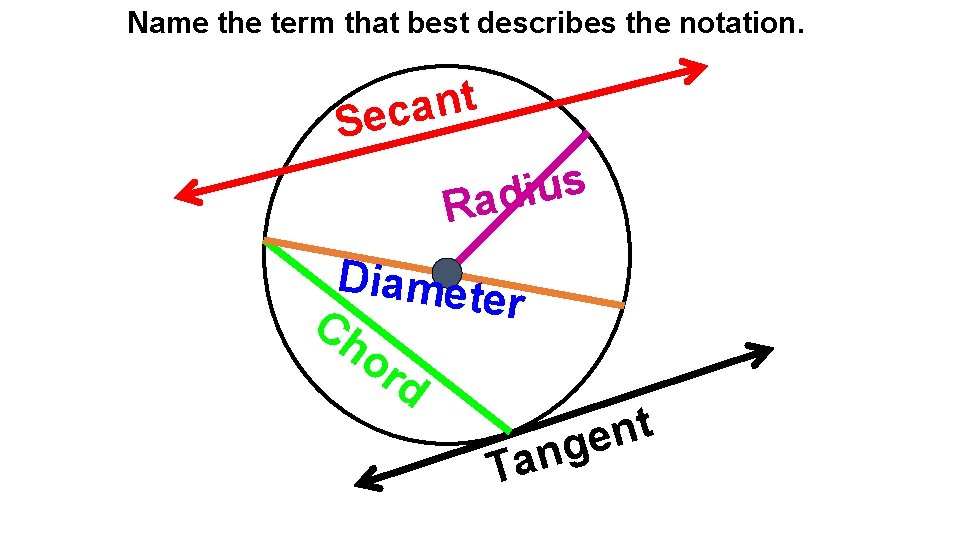
Name the term that best describes the notation. t n a Sec s u i d Ra Diamet e r Ch or d n a T t n ge

Central Angles An angle whose vertex is at the center of the circle

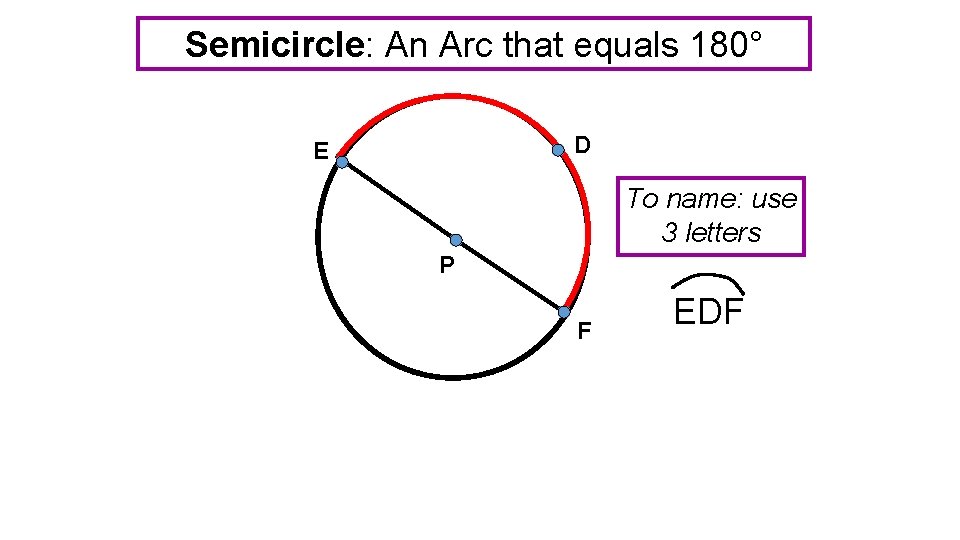
Semicircle: An Arc that equals 180° D E To name: use 3 letters P F EDF

THINGS TO KNOW AND REMEMBER ALWAYS A circle has 360 degrees A semicircle has 180 degrees Vertical Angles are CONGRUENT Linear Pairs are SUPPLEMENTARY

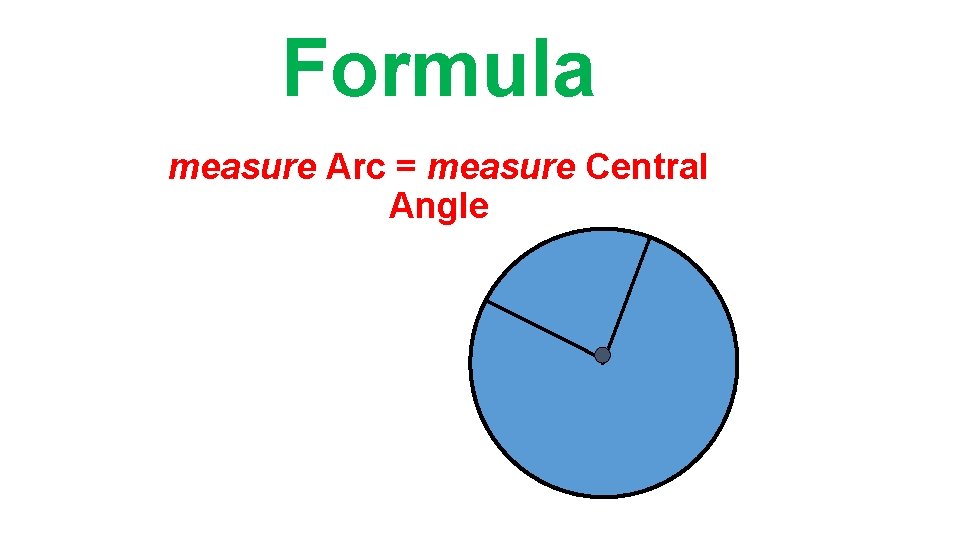
Formula measure Arc = measure Central Angle

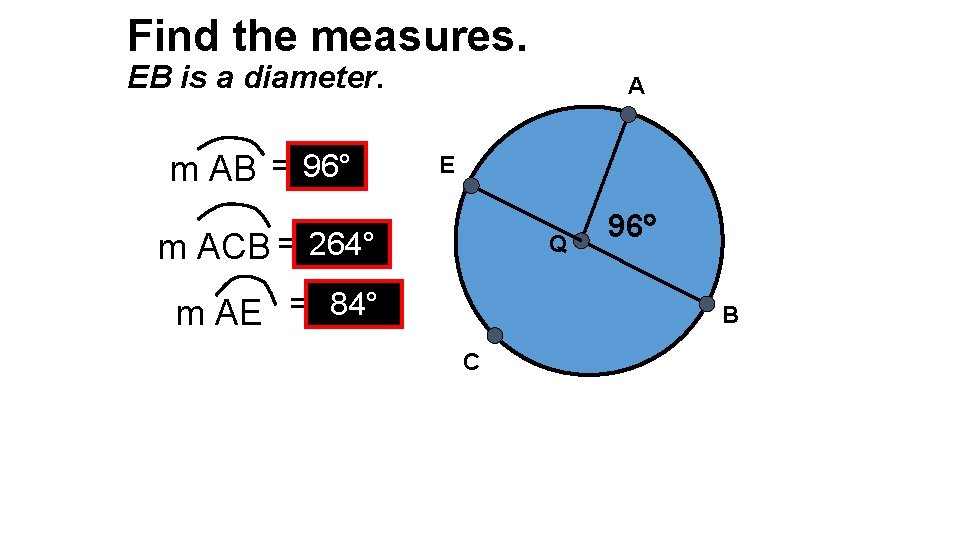
Find the measures. EB is a diameter. m AB = 96° A E m ACB = 264° Q m AE = 84° 96 B C

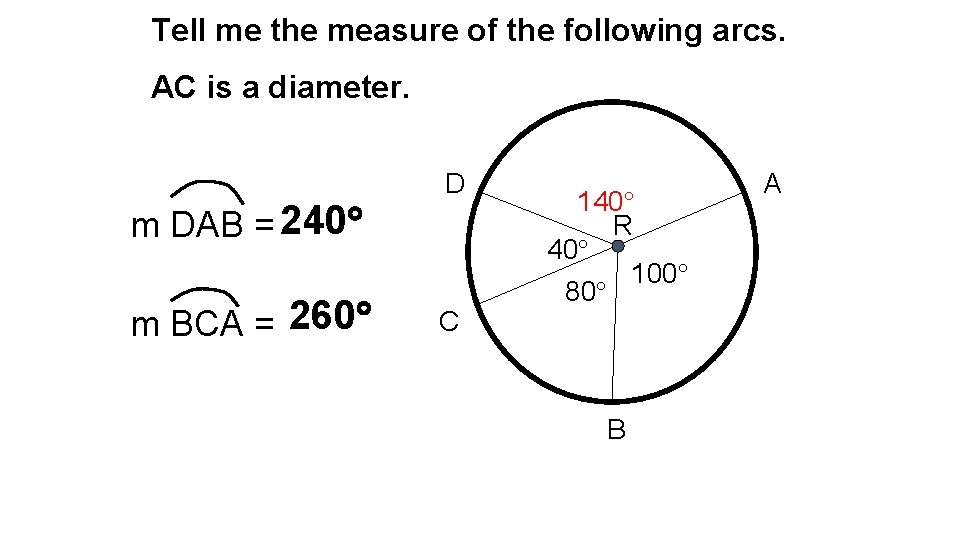
Tell me the measure of the following arcs. AC is a diameter. m DAB = 240 m BCA = 260 D C 140 R 40 100 80 B A

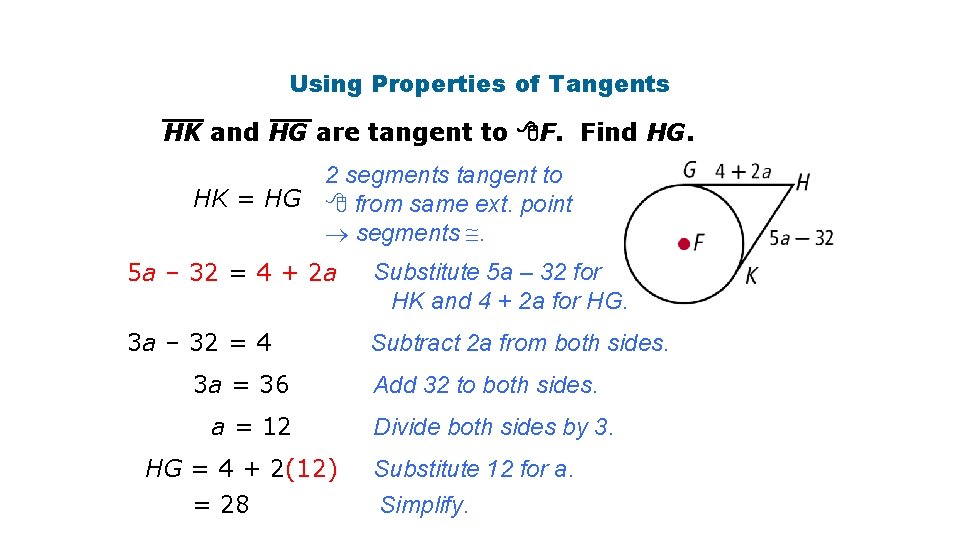
Using Properties of Tangents HK and HG are tangent to F. Find HG. HK = HG 2 segments tangent to from same ext. point segments . 5 a – 32 = 4 + 2 a Substitute 5 a – 32 for HK and 4 + 2 a for HG. 3 a – 32 = 4 Subtract 2 a from both sides. 3 a = 36 a = 12 HG = 4 + 2(12) = 28 Add 32 to both sides. Divide both sides by 3. Substitute 12 for a. Simplify.

Applying Congruent Angles, Arcs, and Chords TV WS. Find m. WS. TV WS m. TV = m. WS 9 n – 11 = 7 n + 11 chords have arcs. Def. of arcs Substitute the given measures. Subtract 7 n and add 11 to both sides. 2 n = 22 Divide both sides by 2. n = 11 m. WS = 7(11) + 11 Substitute 11 for n. Simplify. = 88°

Example 3 B: Applying Congruent Angles, Arcs, and Chords C J, and m GCD m NJM. Find NM. GD NM GCD NJM GD NM arcs have chords. GD = NM Def. of chords

Find QR to the nearest tenth. Step 1 Draw radius PQ. PQ = 20 Radii of a are . Step 2 Use the Pythagorean Theorem. TQ 2 + PT 2 = PQ 2 Substitute 10 for PT and 20 for PQ. TQ 2 + 102 = 202 Subtract 102 from both sides. TQ 2 = 300 Take the square root of both sides. TQ 17. 3 Step 3 Find QR. QR = 2(17. 3) = 34. 6 PS QR , so PS bisects QR.

The circle graph shows the types of cuisine available in a city. Find m. TRQ. 158. 4

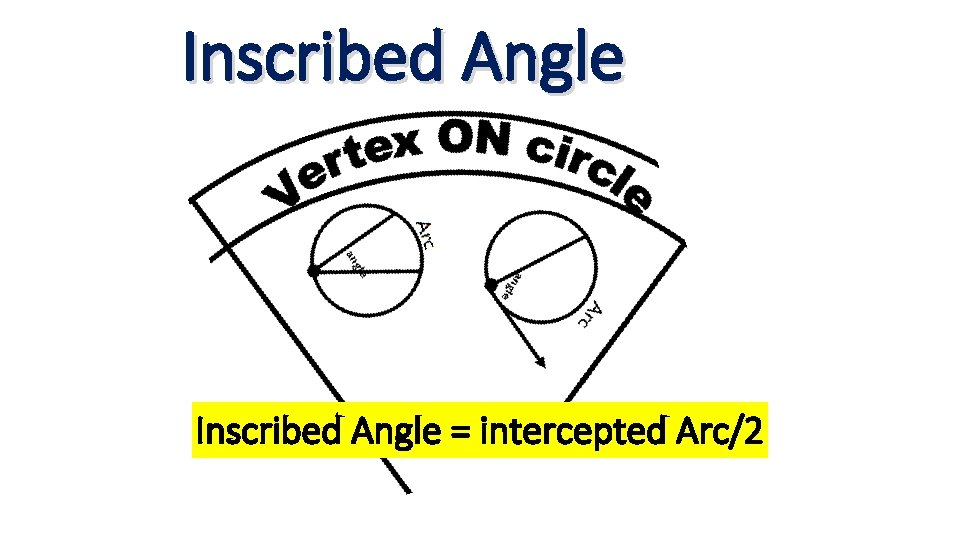
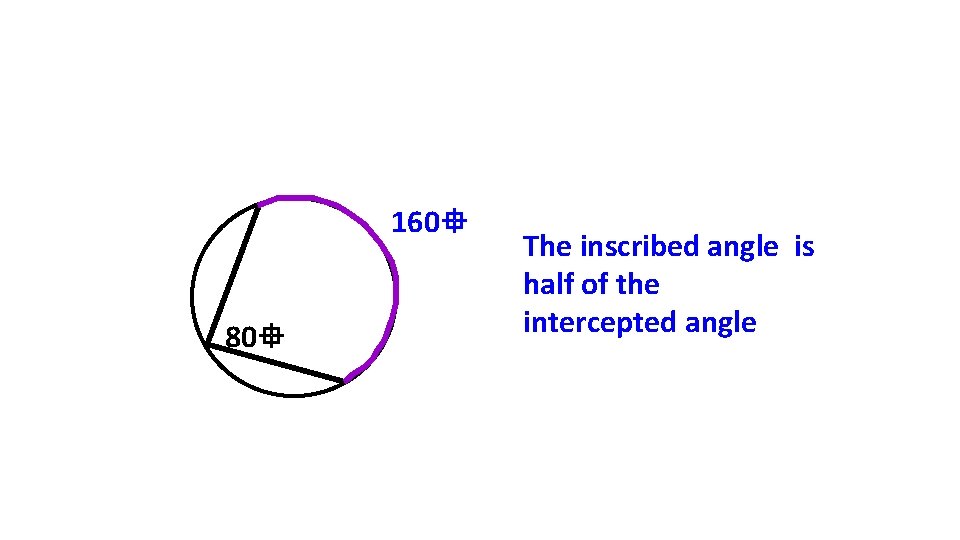
Inscribed Angle = intercepted Arc/2

160 80 The inscribed angle is half of the intercepted angle

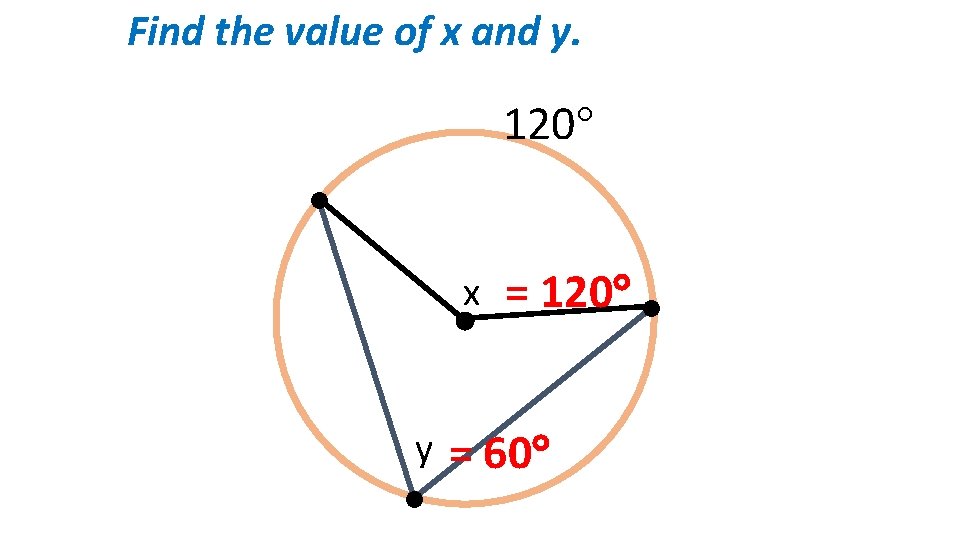
Find the value of x and y. 120 x y = 120 = 60
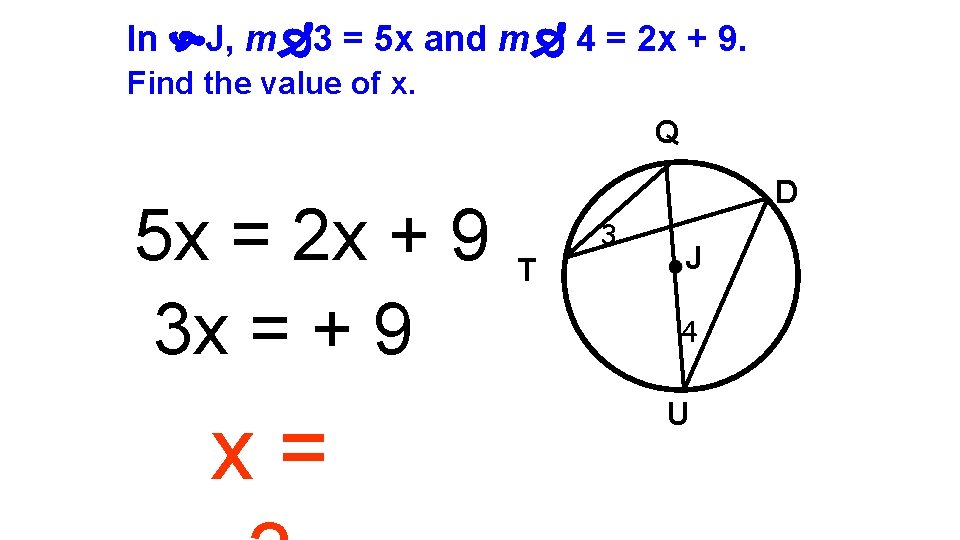
In J, m 3 = 5 x and m 4 = 2 x + 9. Find the value of x. Q 5 x = 2 x + 9 3 x = + 9 x= D T 3 J 4 U

Example 4 In K, GH is a diameter and m GNH = 4 x – 14. Find the value of x. 4 x – 14 = 90 4 x = 104 G x = 26 H K N

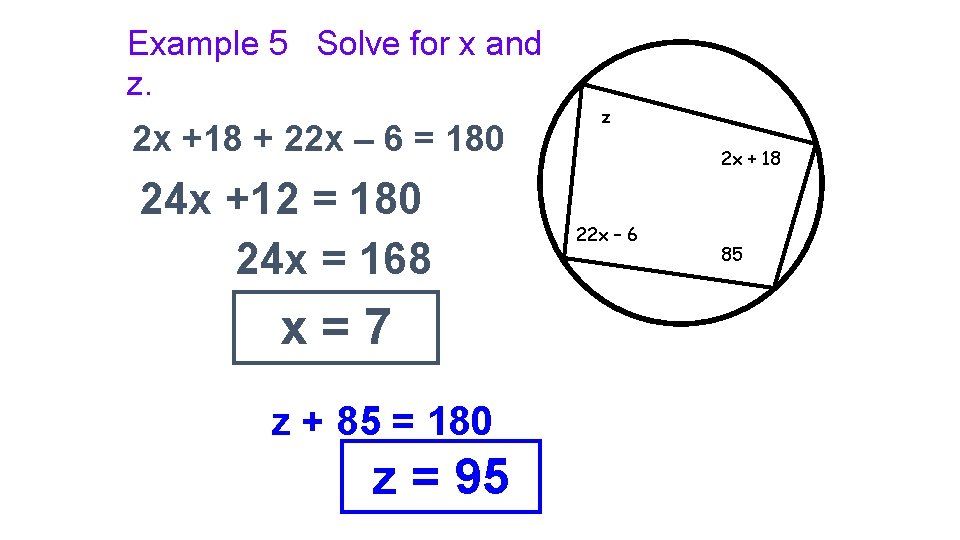
Example 5 Solve for x and z. 2 x +18 + 22 x – 6 = 180 24 x +12 = 180 24 x = 168 x=7 z + 85 = 180 z = 95 z 2 x + 18 22 x – 6 85

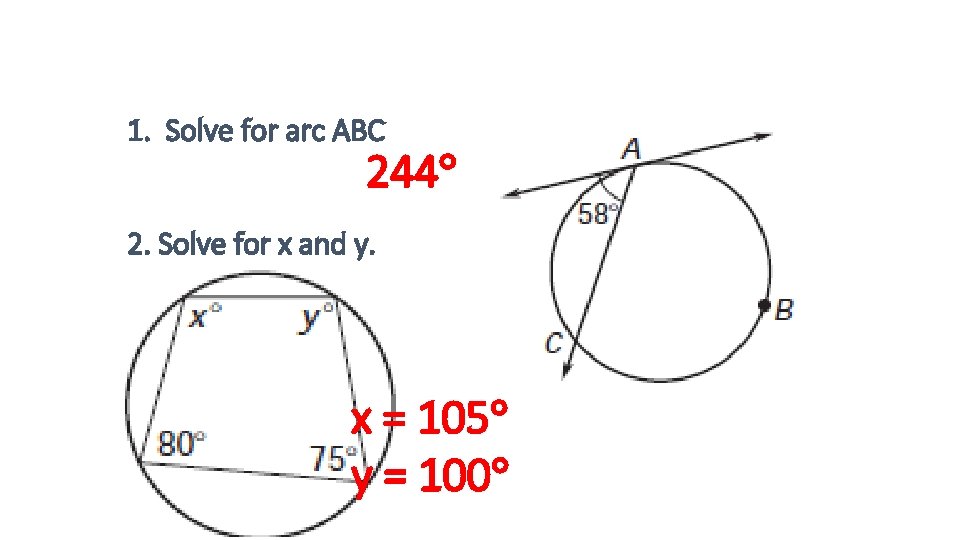
1. Solve for arc ABC 244 2. Solve for x and y. x = 105 y = 100

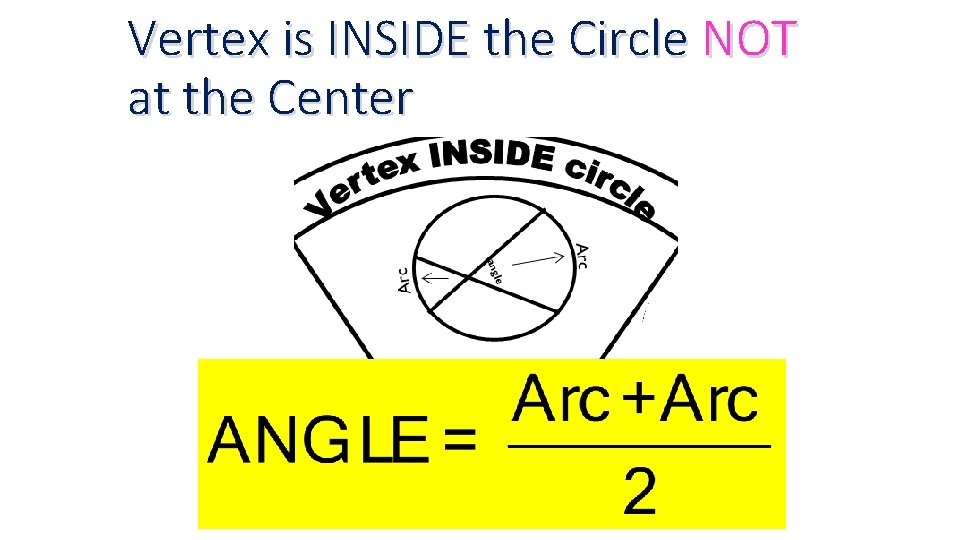
Vertex is INSIDE the Circle NOT at the Center

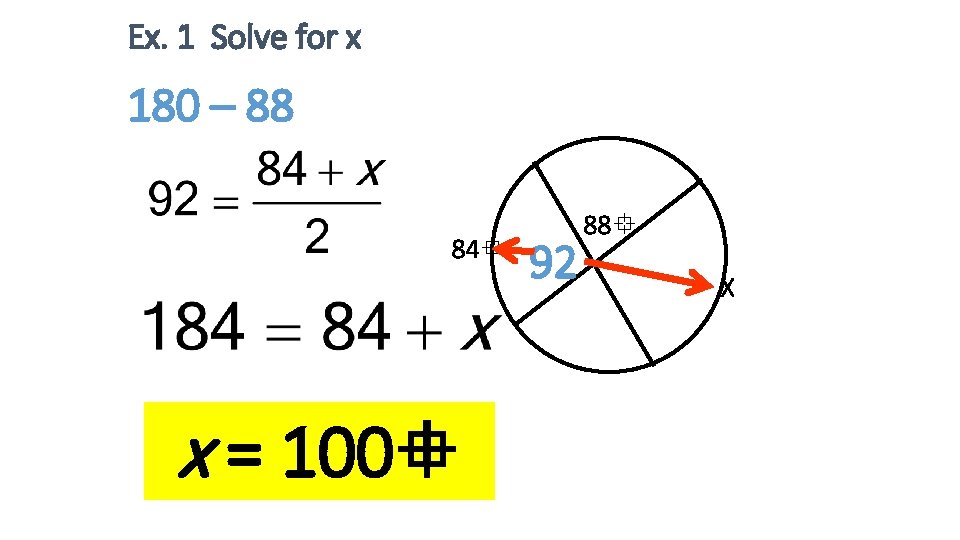
Ex. 1 Solve for x 180 – 88 84 x = 100 92 88 X

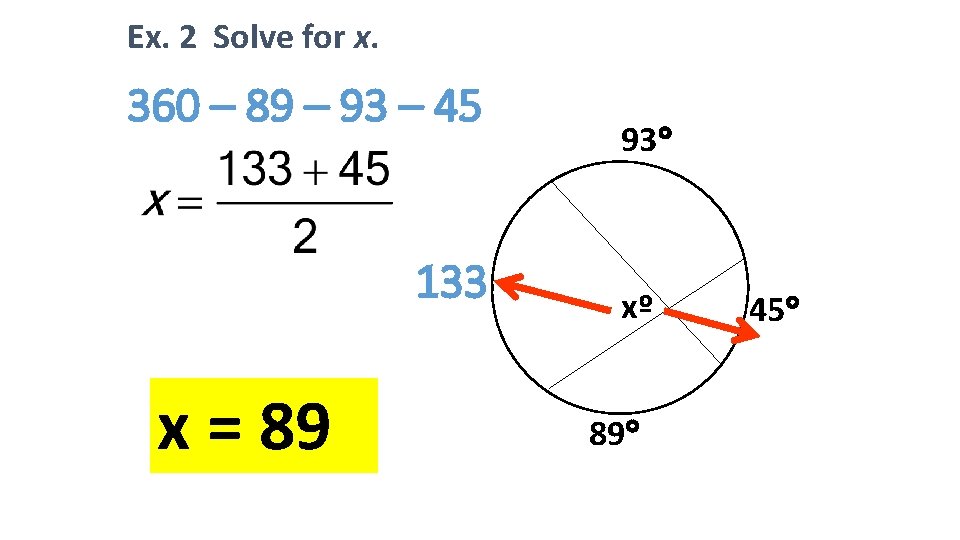
Ex. 2 Solve for x. 360 – 89 – 93 – 45 133 x = 89 93 xº 89 45

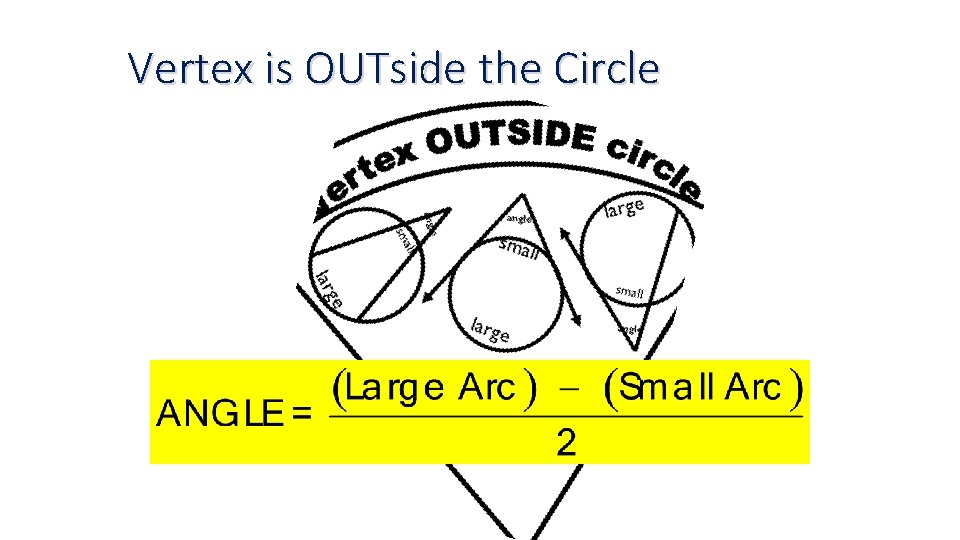
Vertex is OUTside the Circle
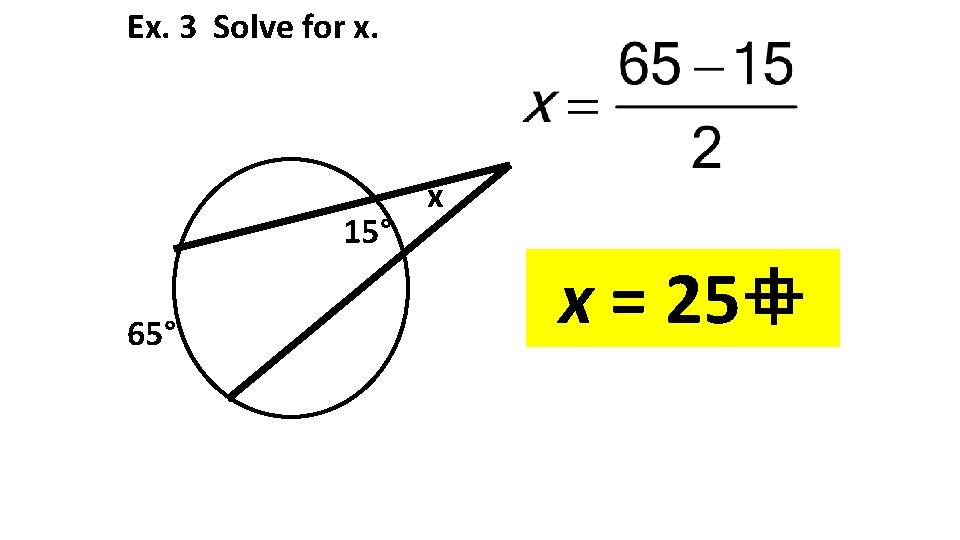
Ex. 3 Solve for x. 15° 65° x x = 25

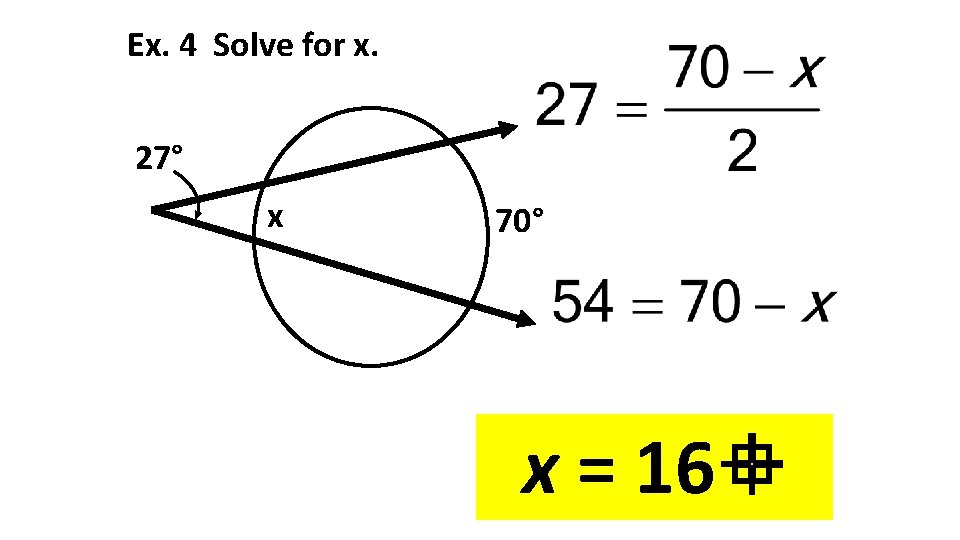
Ex. 4 Solve for x. 27° x 70° x = 16

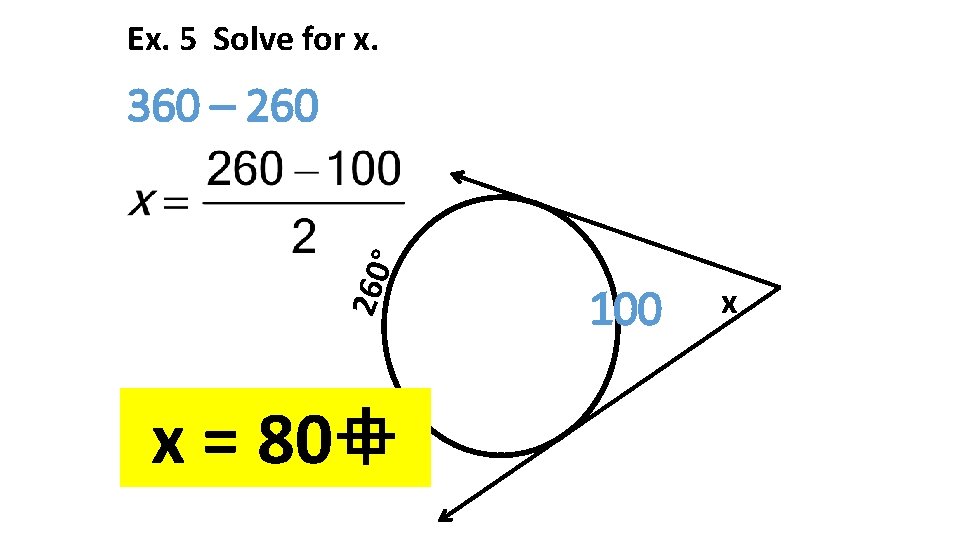
Ex. 5 Solve for x. 260 ° 360 – 260 x = 80 100 x

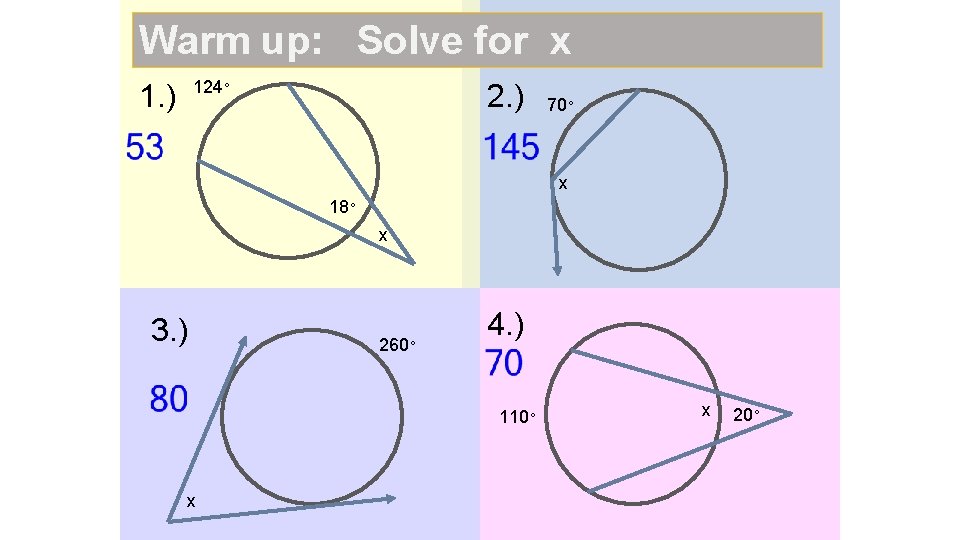
Warm up: Solve for x 124◦ 1. ) 2. ) 70◦ x 18◦ x 3. ) 260◦ 4. ) 110◦ x x 20◦

Circumference, Arc Length, Area, and Area of Sectors

Find the EXACT circumference. 1. r = 14 feet 2. d = 15 miles

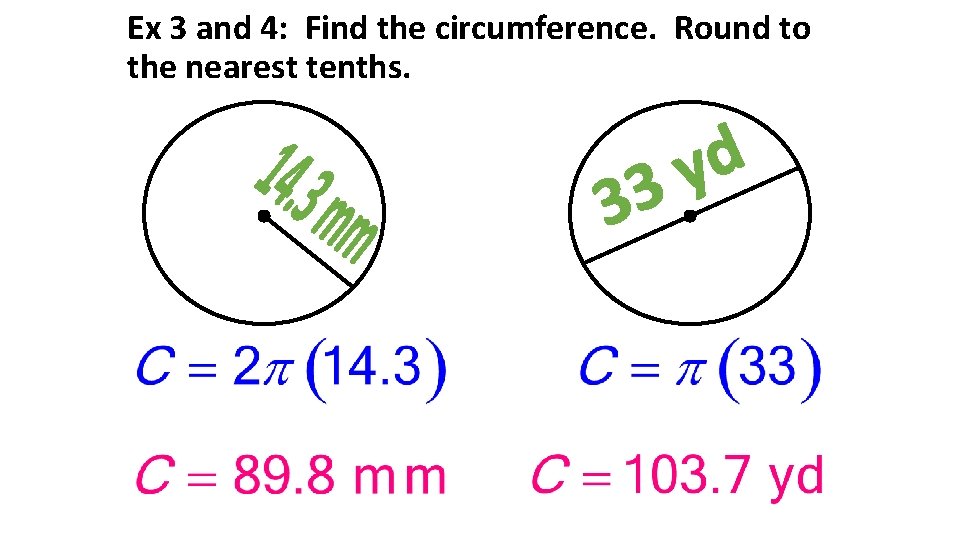
Ex 3 and 4: Find the circumference. Round to the nearest tenths.

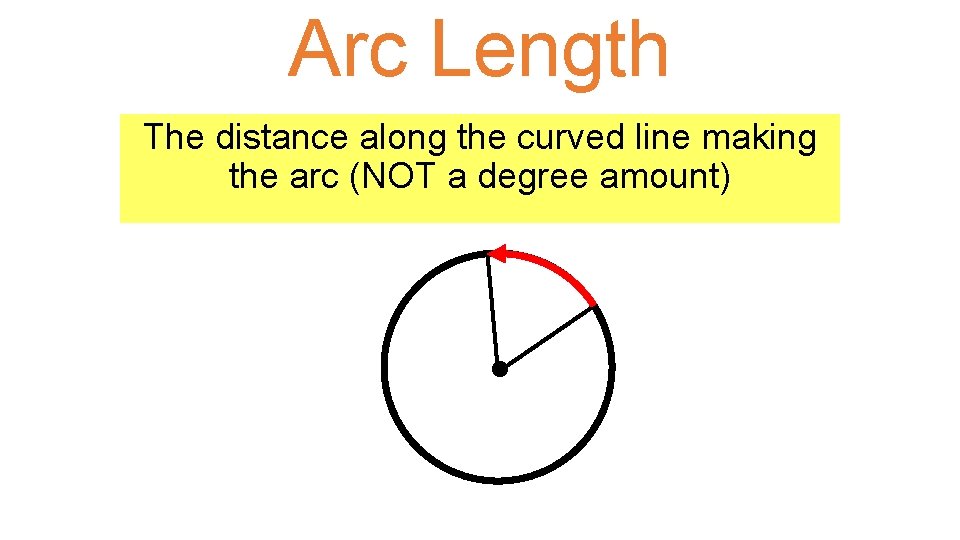
Arc Length The distance along the curved line making the arc (NOT a degree amount)

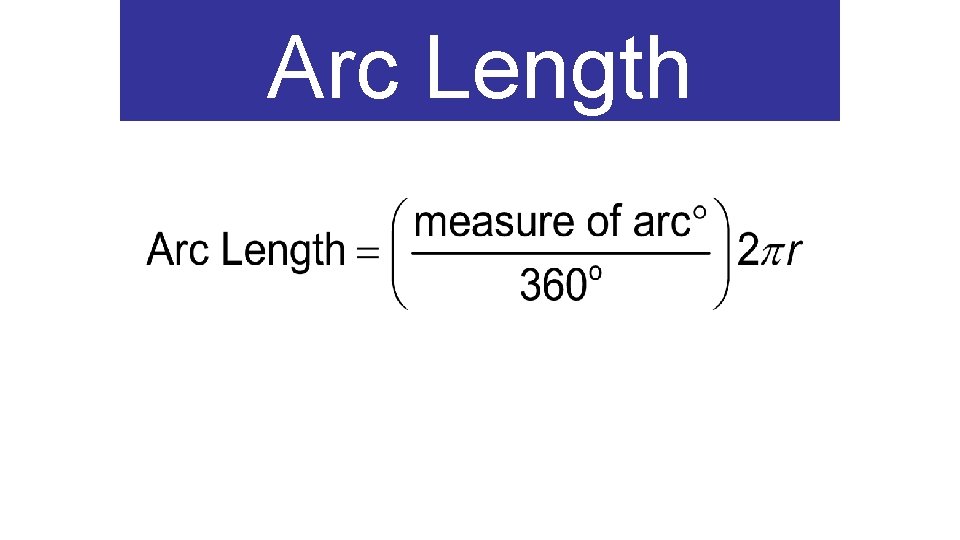
Arc Length

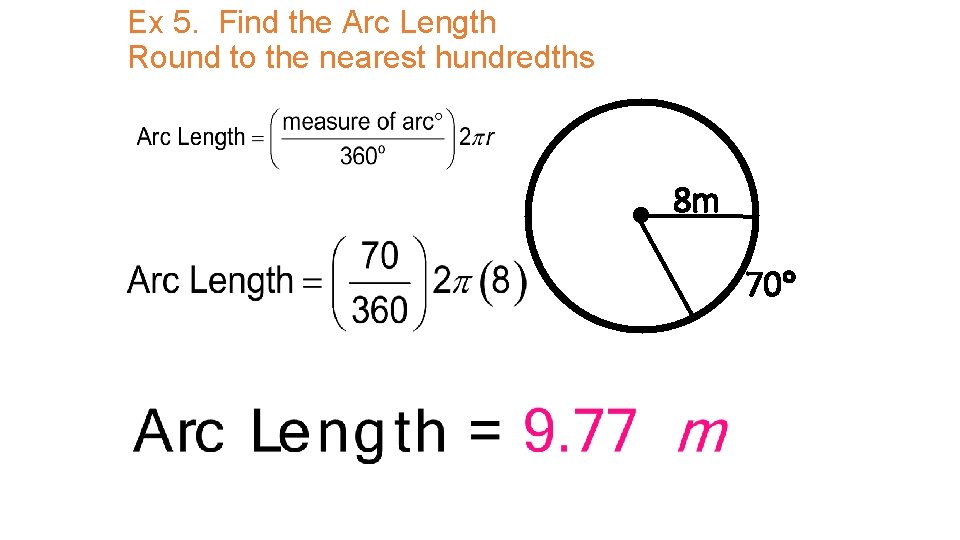
Ex 5. Find the Arc Length Round to the nearest hundredths 8 m 70

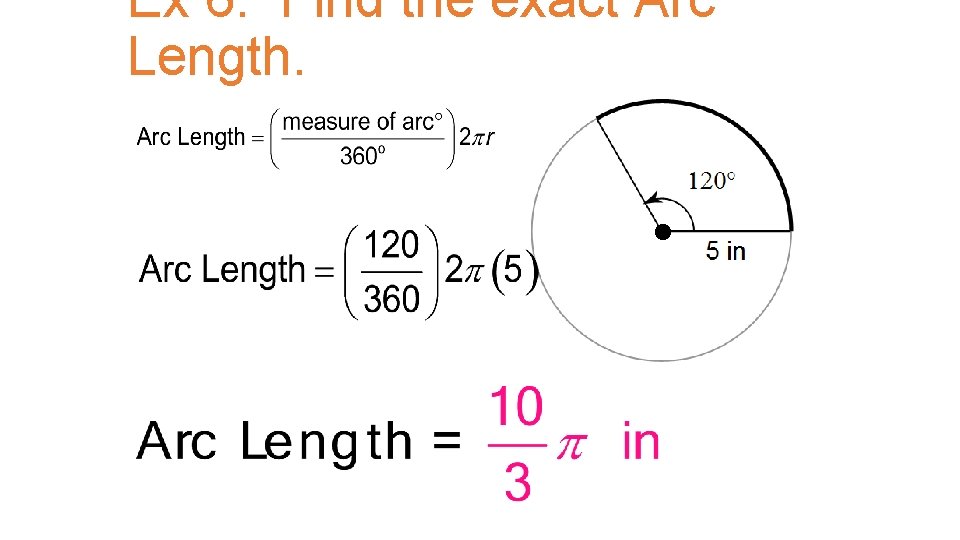
Ex 6. Find the exact Arc Length.

Ex 7. What happens to the arc length if the radius were to be doubled? Halved?

Area of Circles The amount of space occupied. r A= 2 pr

Find the EXACT area. 8. r = 29 feet 9. d = 44 miles

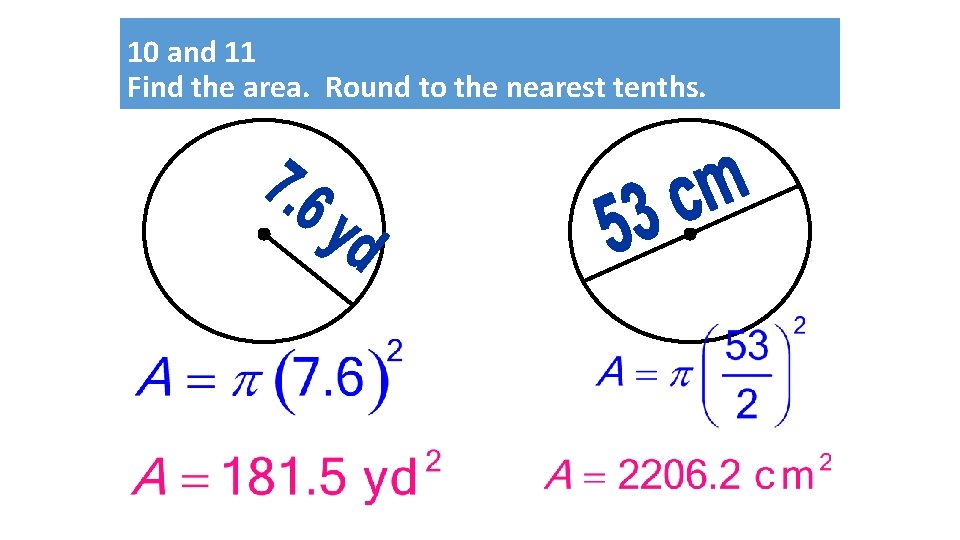
10 and 11 Find the area. Round to the nearest tenths.

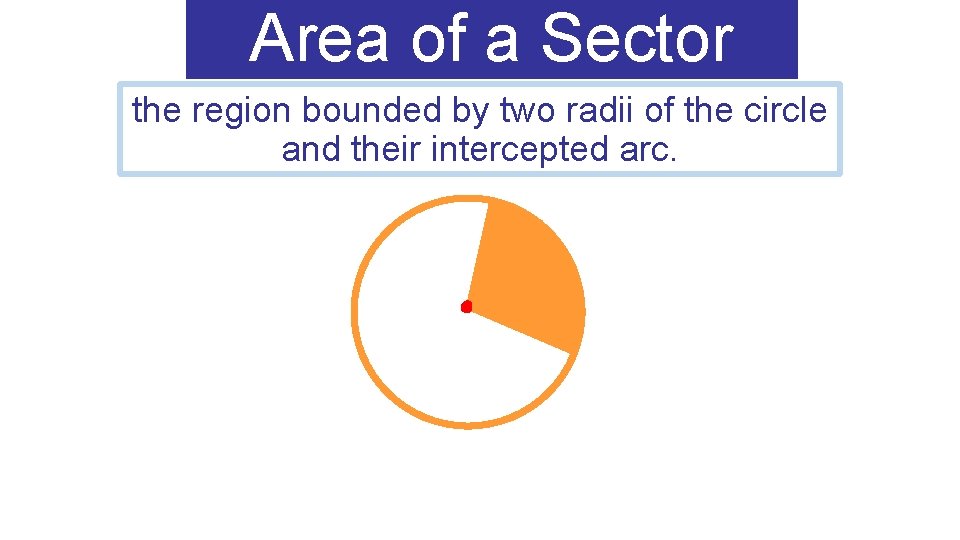
Area of a Sector the region bounded by two radii of the circle and their intercepted arc.

Area of a Sector

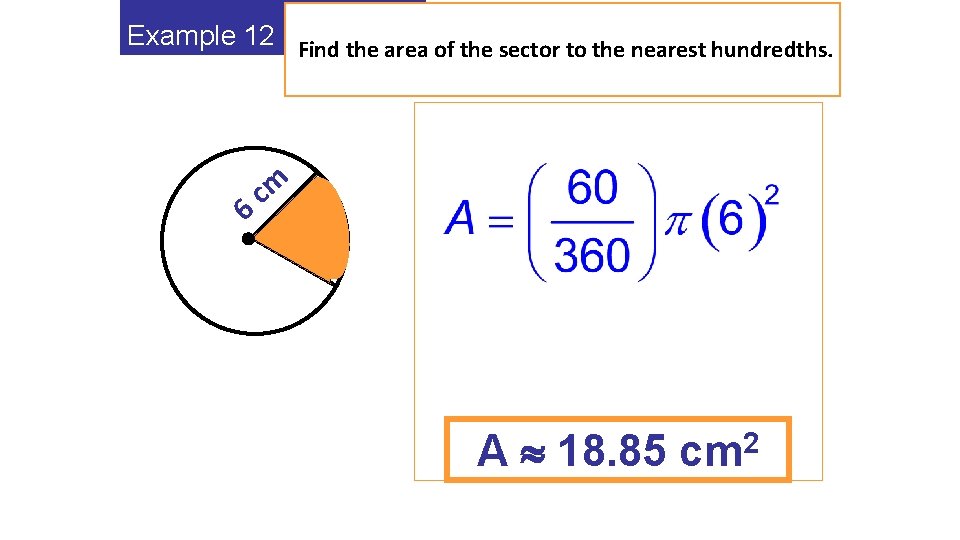
Example 12 Find the area of the sector to the nearest hundredths. 6 cm R 60 Q A 18. 85 cm 2

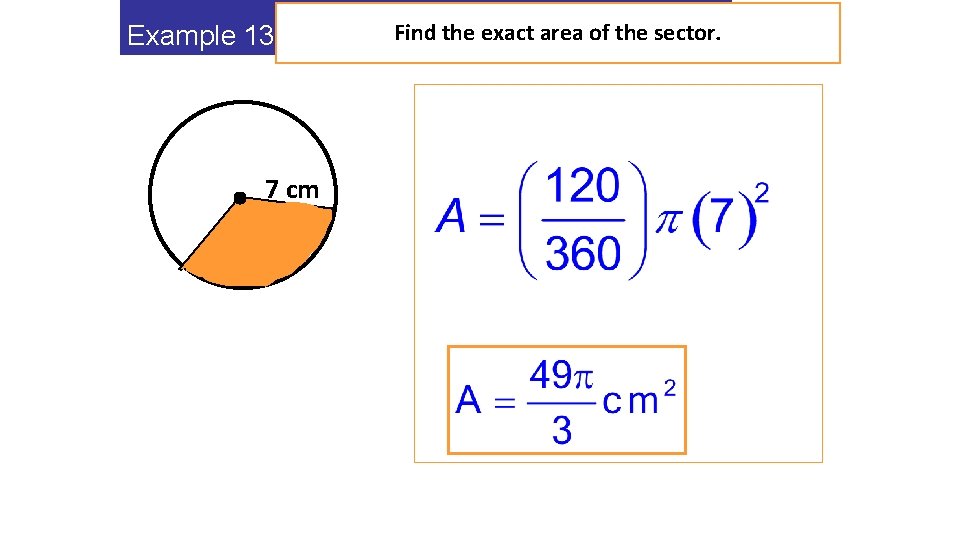
Find the exact area of the sector. Example 13 6 cm 7 cm Q 120 R

Area of minor segment = Example 14 (Area of sector) – (Area of triangle) R 12 yd Q