Diagnostics Checking Assumptions and Bad Data Questions What

Diagnostics Checking Assumptions and Bad Data

Questions • What is the linearity assumption? How can you tell if it seems met? • What is homoscedasticity (heteroscedasticity)? How can you tell if it’s a problem? • What is an outlier? • What is leverage? • What is a residual? • How can you use residuals in assuring that the regression model is a good representation of the data? • Why consider a standardized residual? • What is a studentized residual?

Linear Model • Linear relations b/t X and Y • Normal distribution of error of prediction • Homoscedasticity (homogeneity of error in Y across levels of X)

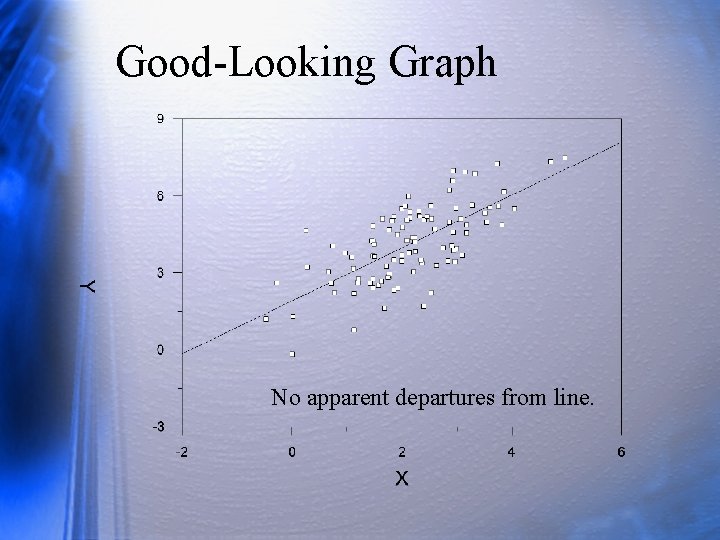
Good-Looking Graph No apparent departures from line.

Same Data, Different Graph No systematic relations between X and residuals.

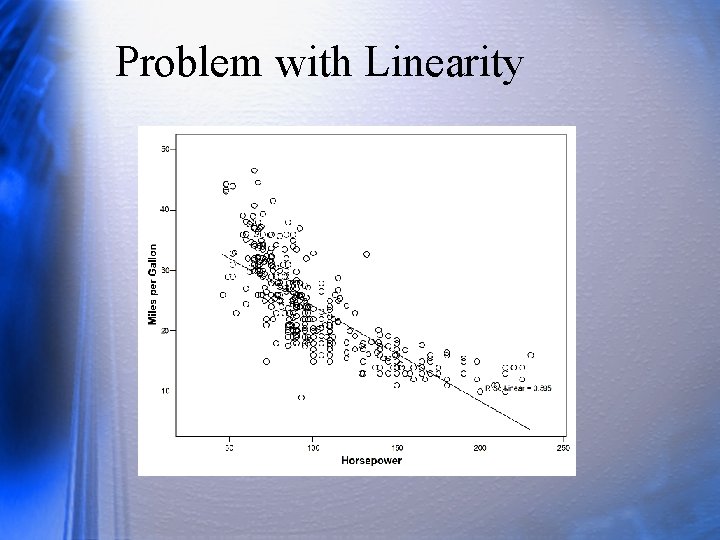
Problem with Linearity

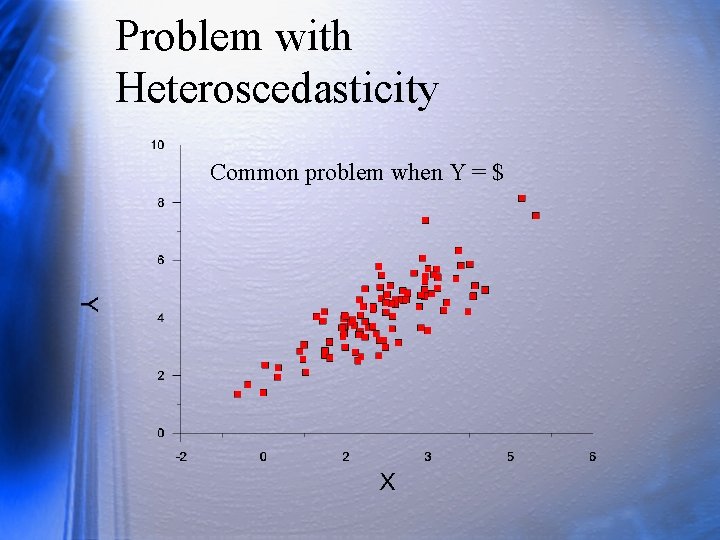
Problem with Heteroscedasticity Common problem when Y = $

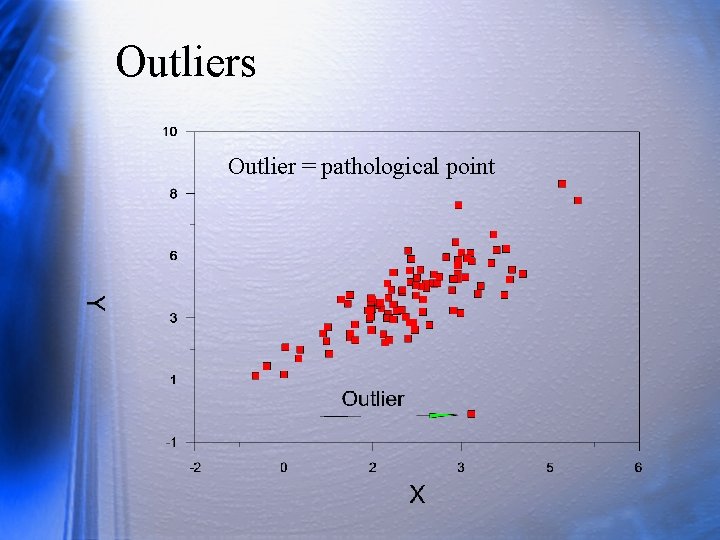
Outliers Outlier = pathological point

Review • What is the linearity assumption? How can you tell if it seems met? • What is homoscedasticity (heteroscedasticity)? How can you tell if it’s a problem? • What is an outlier?

Residuals • Zresid • Look for large values (some say |z|>2) • Studentized residual (Student Residual): The studentized residual considers the distance of the point from the mean. The farther X is from the mean, the smaller the standard error and the larger the residual. Look for large values. Also, studentized deleted residual (RStudent).

Influence Analysis • Leverage: • Leverage is an index of the importance of an observation to a regression analysis. – Function of X only – Large deviations from mean are influential – Maximum is 1; min is 1/N – Average value is (k+1)/N, where k is the number of IVs

Influence Analysis (2) • DFBETA and standardized DFBETA • Change in slope or intercept resulting when you delete the ith person. • Allow for influence of both X and Y

Example X M= Y 2 2 3 3 3 1 4 3 5 2 8 8 4. 14 2. 86 r =. 82; r 2 =. 67; p <. 05. SX = 1. 95, SY = 2. 41 b=1. 01, a=-1. 34

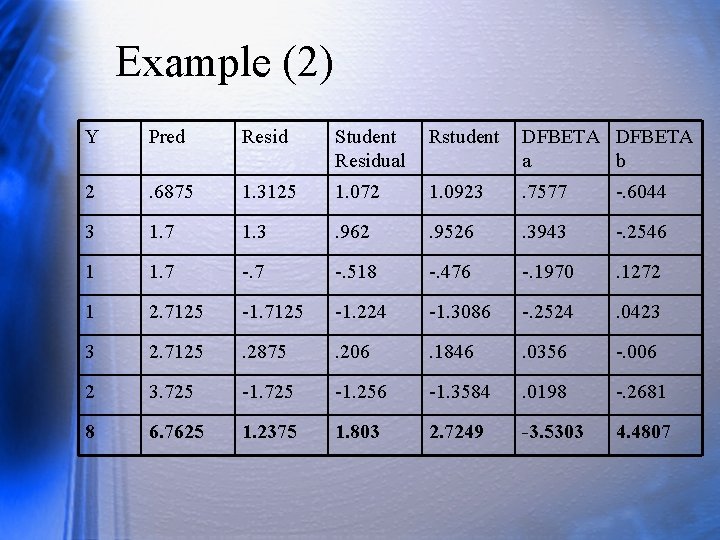
Example (2) Y Pred Resid Student Residual Rstudent DFBETA a b 2 . 6875 1. 3125 1. 072 1. 0923 . 7577 -. 6044 3 1. 7 1. 3 . 962 . 9526 . 3943 -. 2546 1 1. 7 -. 518 -. 476 -. 1970 . 1272 1 2. 7125 -1. 224 -1. 3086 -. 2524 . 0423 3 2. 7125 . 2875 . 206 . 1846 . 0356 -. 006 2 3. 725 -1. 256 -1. 3584 . 0198 -. 2681 8 6. 7625 1. 2375 1. 803 2. 7249 -3. 5303 4. 4807

Remedies • Fit Curves if needed. • Note heteroscedasticity for applied problems. • Investigate all outliers. May delete them or not, depending. Report your actions.

Review • What is leverage? • What is a residual? • How can you use residuals in assuring that the regression model is a good representation of the data? • Why consider a standardized residual? • What is a studentized residual?