Diagnostic and Detection Fault Collapsing for Multiple Output

Diagnostic and Detection Fault Collapsing for Multiple Output Circuits Raja K. K. R. Sandireddy and Vishwani D. Agrawal Dept. Of Electrical and Computer Engineering, Auburn University, Auburn, AL-36849 USA.

Outline v Introduction Ø Fault Equivalence and Fault Dominance Ø Functional collapsing v v Fault Equivalence and Dominance definitions Results of functional collapsing Hierarchical fault collapsing Conclusions and Future work. 2

Equivalence R Structural equivalence 1: Two faults f 1 and f 2 are said to be R structurally equivalent if they produce the same reduced circuit graph [netlist] when faulty values are implied and constant edges [signals] are removed. Functional equivalence 1: Two faults f 1 and f 2 are said to be functionally equivalent if they modify the Boolean function of the circuit in the same way, i. e. , they yield the same output functions. E. J. Mc. Cluskey and F. W. Clegg, “Fault Equivalence in Combinational Logic Networks, ” IEEE Trans. Computers, vol. C-20, no. 11, Nov. 1971, pp. 1286 -1293. 1 3

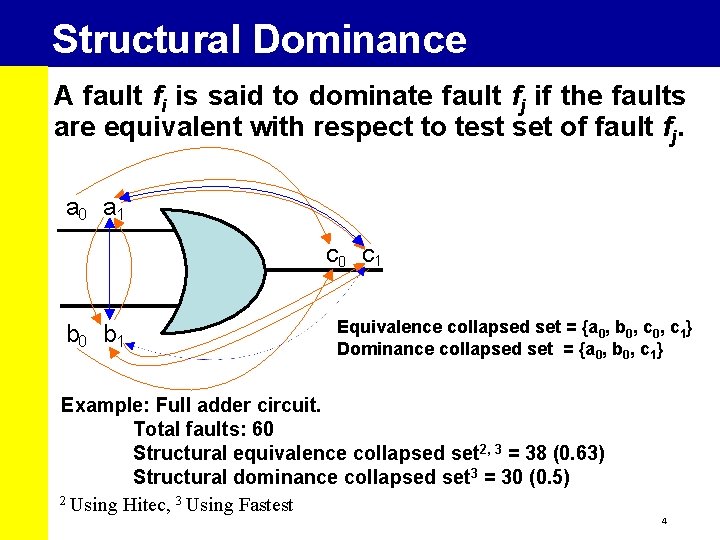
Structural Dominance A fault fi is said to dominate fault fj if the faults are equivalent with respect to test set of fault fj. a 0 a 1 c 0 c 1 b 0 b 1 Equivalence collapsed set = {a 0, b 0, c 1} Dominance collapsed set = {a 0, b 0, c 1} Example: Full adder circuit. Total faults: 60 Structural equivalence collapsed set 2, 3 = 38 (0. 63) Structural dominance collapsed set 3 = 30 (0. 5) 2 Using Hitec, 3 Using Fastest 4

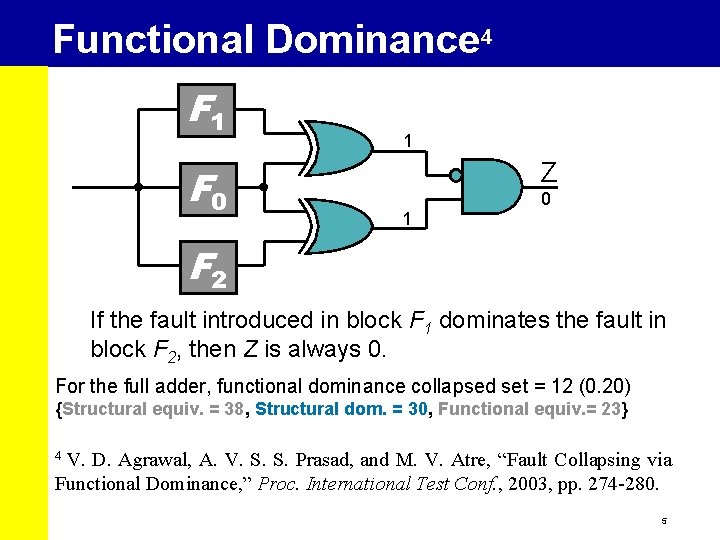
Functional Dominance 4 F 1 F 0 1 Z 1 0 F 2 If the fault introduced in block F 1 dominates the fault in block F 2, then Z is always 0. For the full adder, functional dominance collapsed set = 12 (0. 20) {Structural equiv. = 38, Structural dom. = 30, Functional equiv. = 23} V. D. Agrawal, A. V. S. S. Prasad, and M. V. Atre, “Fault Collapsing via Functional Dominance, ” Proc. International Test Conf. , 2003, pp. 274 -280. 4 5

Equivalence Definitions For multiple output circuits, v Diagnostic Equivalence - Two faults of a Boolean circuit are called diagnostically equivalent if and only if the functions of the two faulty circuits are identical at each output. v Detection Equivalence - Two faults are called detection equivalent if and only if all tests that detect one fault also detect the other fault, not necessarily at the same output. A B s-a-0 c Y Z s-a-0 The faults c 0 and Y 0 are detection equivalent faults, but not diagnostic equivalent. For the full adder, diagnostic equivalence collapsed set = 26 (0. 43), detection equivalence collapsed set = 23 (0. 38) {Structural equiv. = 38, Structural dom. = 30, Functional equiv. = 26, Functional dom. = 12} 6

Dominance Definitions v Fault Dominance 5 - A fault fi is said to dominate fault fj if (a) the set of all vectors that detects fault fj is a subset of all vectors that detects fault fi and (b) each vector that detects fj implies identical values at the corresponding outputs of faulty versions of the circuit. Conventionally dominance is defined as: v A fault fi is said to dominate fault fj if the faults are equivalent with respect to test set of fault fj. v If all tests of fault fj detect another fault fi, then fi is said to dominate fj. 5 J. F. Poage, “Derivation of Optimum Tests to Detect Faults in Combinational Circuits", Proc. Symposium on Mathematical Theory of Automata, 1962, pp. 483 -528. 7

Dominance Definitions contd. For multiple output circuits, the two possible interpretations of dominance: v Diagnostic dominance - If all tests of a fault f 1 detect another fault f 2 on the exact same outputs where f 1 was detected, then f 2 is said to diagnostically dominate f 1. v Detection dominance - If all tests of a fault f 1 detect another fault f 2, irrespective of the output where f 1 was detected, then f 2 is said to detection dominate f 1. Diagnostic dominance implies detection dominance. For the full adder, diagnostic dominance collapsed set = 12 (0. 2) detection dominance collapsed set = 6 (0. 1) {Structural equiv. = 38, Structural dom. = 30, Diagnostic equiv. = 26, Detection equiv. = 23} 8

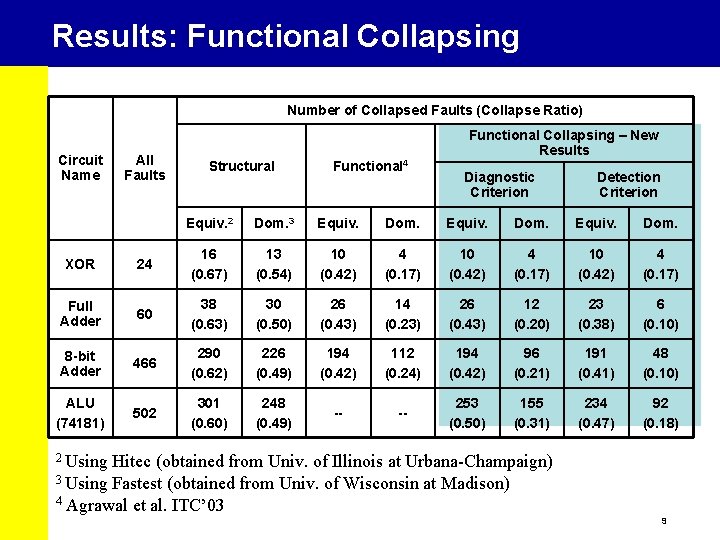
Results: Functional Collapsing Number of Collapsed Faults (Collapse Ratio) Circuit Name All Faults Structural Functional 4 Functional Collapsing – New Results Diagnostic Criterion Detection Criterion Equiv. 2 Dom. 3 Equiv. Dom. XOR 24 16 (0. 67) 13 (0. 54) 10 (0. 42) 4 (0. 17) Full Adder 60 38 (0. 63) 30 (0. 50) 26 (0. 43) 14 (0. 23) 26 (0. 43) 12 (0. 20) 23 (0. 38) 6 (0. 10) 8 -bit Adder 466 290 (0. 62) 226 (0. 49) 194 (0. 42) 112 (0. 24) 194 (0. 42) 96 (0. 21) 191 (0. 41) 48 (0. 10) ALU (74181) 502 301 (0. 60) 248 (0. 49) -- -- 253 (0. 50) 155 (0. 31) 234 (0. 47) 92 (0. 18) 2 Using Hitec (obtained from Univ. of Illinois at Urbana-Champaign) 3 Using Fastest (obtained from Univ. of Wisconsin at Madison) 4 Agrawal et al. ITC’ 03 9

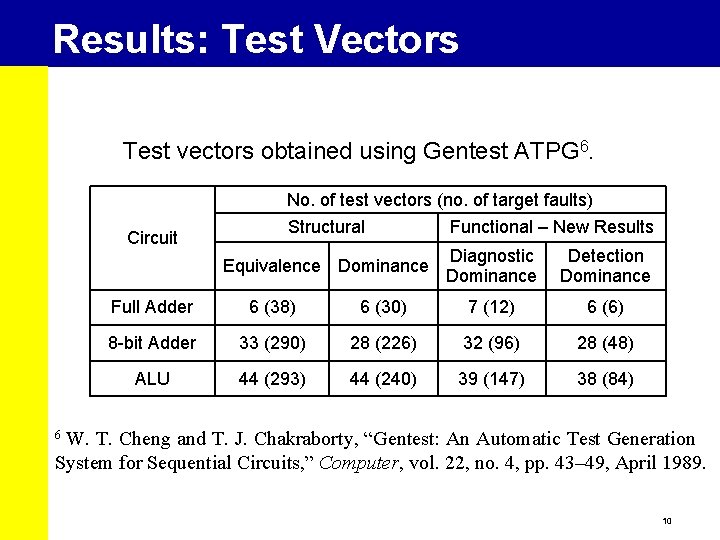
Results: Test Vectors Test vectors obtained using Gentest ATPG 6. No. of test vectors (no. of target faults) Circuit Structural Equivalence Dominance Functional – New Results Diagnostic Dominance Detection Dominance Full Adder 6 (38) 6 (30) 7 (12) 6 (6) 8 -bit Adder 33 (290) 28 (226) 32 (96) 28 (48) ALU 44 (293) 44 (240) 39 (147) 38 (84) W. T. Cheng and T. J. Chakraborty, “Gentest: An Automatic Test Generation System for Sequential Circuits, ” Computer, vol. 22, no. 4, pp. 43– 49, April 1989. 6 10

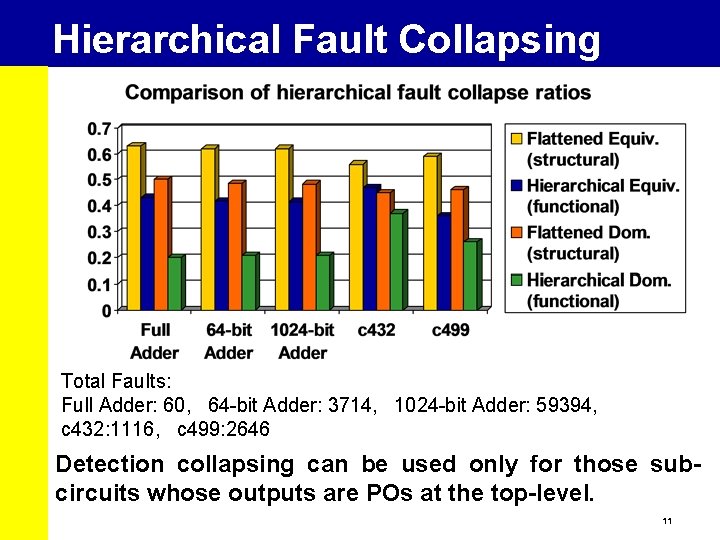
Hierarchical Fault Collapsing Total Faults: Full Adder: 60, 64 -bit Adder: 3714, 1024 -bit Adder: 59394, c 432: 1116, c 499: 2646 Detection collapsing can be used only for those subcircuits whose outputs are POs at the top-level. 11

CPU time (sec) for hierarchical collapsing c ite ed n tte la F ) (H m ra g ro P r u F d ne te t la ) (O l o w l) t l( a ic m H h rc e lev i- ch ar r ie l) e ev ic ( al ult a er i H 12

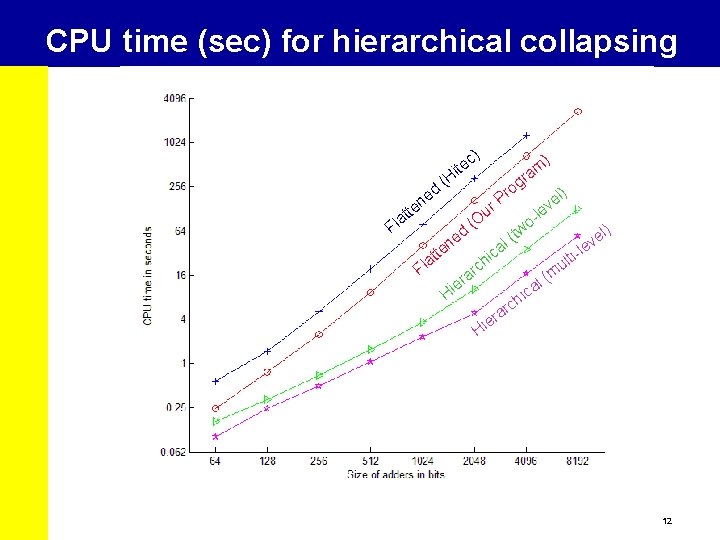
Conclusions v Diagnostic and detection collapsing should be used only with smaller circuits. v Collapse ratios using detection dominance collapsing is about 10 -20%. v Hierarchical fault collapsing: Ø Better (lower) collapse ratios due to functional collapsed library Ø Order of magnitude reduction in collapse time. v Smaller fault sets: Ø Fewer test vectors Ø Reduced fault simulation effort Ø Easier fault diagnosis. v Use caution when using dominance collapsing!! 13

Future Work v Generate fault collapsing library of standard cells (Mentor Graphics, etc. ). v Efficient redundancy detection program. v Customized ATPG to obtain minimal test vector set. 14