devin Konusu Matrisler Yararlanlan Kaynaklar Tmay Set 5






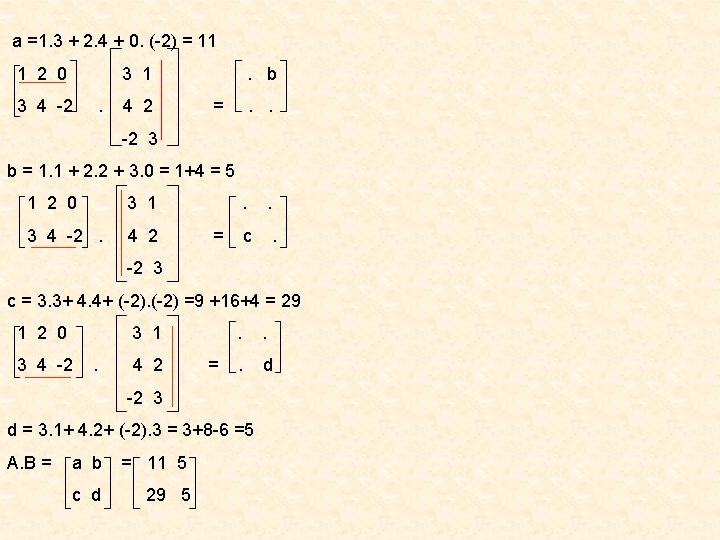
















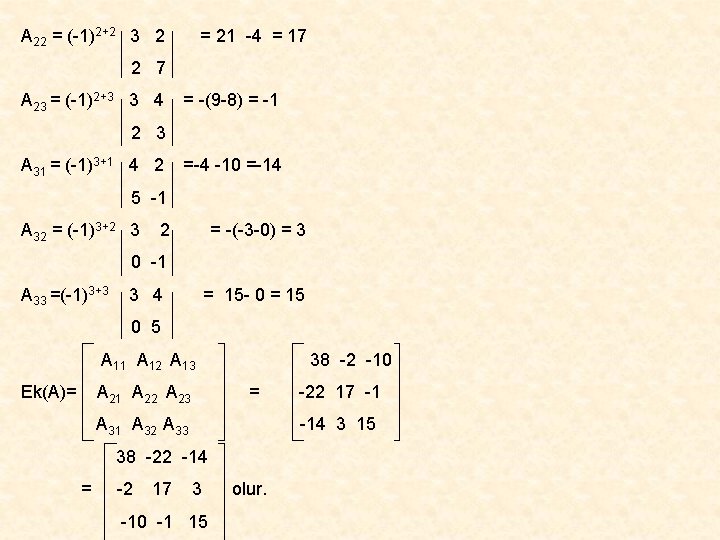








- Slides: 32

Ödevin Konusu : Matrisler Yararlanılan Kaynaklar : Tümay Set 5 Öysm Çözümlü Soru Bankası Öğretmenin Adı:

MATRİSLER • Tanım: a 11 a 12 …a 1 n a) A= A= a 21 a 22 …a 2 n ………………. am 1 am 2… amn Biçiminde bir cismin elemanlarının sıralı bir tablosuna mxn türünde bir matris denir. m sayısına matrisin satır sayısı n sayısına ise matrisin sütun sayısı denir. m satırlı ve n sütunlu bir matrise mxn boyutlu ya da mxn türünde bir matris adı verilir. 34 20 56 b) Yukarıdaki matriste 3 satır ve 2 sütun olduğundan A matrisi 3 x 2 türünden bir matristir. 2 1 x 1 , 3, 4, 7 1 x 3 , 0, -5 1 x 2 c) 6 1 x 1 , 2 7 2 x 1 birer sütun matrisidir. , 0 0 -3 3 x 1

ÖRNEK: A = a ij 3 x 2 bulunuz. matrisi aij = (-1)i+j. ij biçiminde tanımlanıyor. A matrisini ÇÖZÜM: a 11 a 12 A = a 21 a 22 a 31 a 32 a 11 = (-1)1+1 1. 1=1 a 12 =(-1)1+2. 1. 2 = -2 a 21 =(-1)2+1. 2. 1=-2 a 22 =(-1)2+2. 2. 2 = 4 A 31 =(-1)3+1. 3. 1=3 a 32 =(-1)3+2. 3. 2 = -6 1 -2 A= -2 4 3 -6 3 x 2 KARE MATRİS: Satır ve sütun sayıları eşit olan matrise kare matris denir. Örneğin,

3 4 matrisi 2 x 2 türünde bir matristir. 5 6 SIFIR MATRİSİ: Tüm elemanları 0 olan matristir. MATRİSLERİN EŞİTLİĞİ: A= aij mxn ve B = bij mxn olsun. İ ve j nin her değeri için aij = bij oluyorsa A ile B matrisleri eşittir. Yani ; aij = bij A=B’ dir. ÖRNEK: 2 x+1 6 y-2 7 = 9 6 olması için x+y+z=? 3 3 z -2 2 x+1= 9 x=4 y-2 =3 y=5 x+y+z =12 bulunur. 3 z- 2=7 z=3 BİR MATRİSİN BİR SAYI İLE ÇARPIMI: Bir matrisi bir sayı ile çarpmak demek onun her elemanını o sayı ile çarpmak demektir. A = 3 4 -2 matrisi için 3 a, a/2 matrislerini bulnuz. 6 0 8

3 A = 3 3 4 -2 = 9 12 -6 6 0 -8 18 0 A/2 = ½ 3 4 -2 -24 = 3/2 2 -1 6 0 -8 3 0 -4 MATRİSLERİN TOPLAMI: A ve B aynı türden olan iki matris olsun. A +B , Aile B’ nin karşılıklı elemanları toplanarak elde edilen matristir. A –B = A+(-B)’ dir. ÖRNEK: 3 4 2 -1 A= 1 -2 ve B = 0 4 0 5 5 2 ve A+2 B ve A-B matrislerini bulnuz. ÇÖZÜM: 3 4 A+ 2 B = 1 -2 0 5 2 -1 +2 0 4 5 2 3 4 = 1 -2 0 5 + 4 -2 7 2 0 8 = 1 6 10 4 10 9

3 4 A -B = 1 -2 2 -1 - 3 4 0 5 = 5 2 1 -2 0 5 -2 1 + 0 -4 1 5 = 5 -2 1 -6 -5 3 MATRİSLERİN ÇARPIMI: A matrisi mxn türünde ; B matrisi nxp türünde olsun. A. B matrisi mxp türünde bir matristir. cij , A. B’ nin bir elemanı ise, bu eleman A’nın i. satır vektörü ile B ‘ nin j. sütun vektörünün skaler çarpımına eşittir. UYARI: A ve B matrisleri verilsin. A. B çarpımının yapılabilmesi için A’nın sütun sayısı B’ nin satır sayısına eşit olması gerekir. Buna göre; A mxn. B nxp = c mxp olur. ÖRNEK: 3 1 A= 1 2 0 ve B = 3 4 -2 1 2 0 3 4 -2 4 2 ise A. B matrisini bulunuz. -2 3 3 1 . 4 2 a. = . .
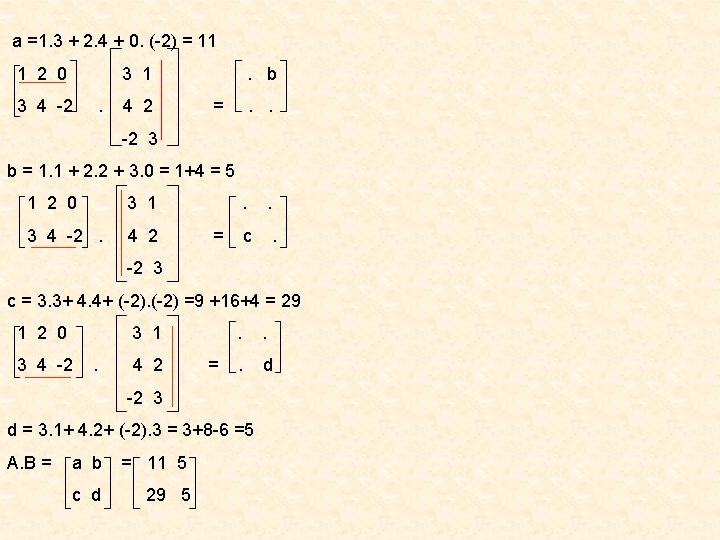
a =1. 3 + 2. 4 + 0. (-2) = 11 1 2 0 3 1 3 4 -2 . 4 2 . b = . . -2 3 b = 1. 1 + 2. 2 + 3. 0 = 1+4 = 5 1 2 0 3 1 3 4 -2. 4 2 . = . c . -2 3 c = 3. 3+ 4. 4+ (-2) =9 +16+4 = 29 1 2 0 3 1 3 4 -2 . 4 2 = . . . d -2 3 d = 3. 1+ 4. 2+ (-2). 3 = 3+8 -6 =5 A. B = a b = 11 5 c d 29 5

ÖRNEK: A = 2 -4 ise A. A = A 2 matrisini bulunuz. 3 -1 ÇÖZÜM : A 2 = A. A = 2 -4 . 3 -1 4 -12 -8 +4 6 -3 -12 +1 = 2 -4 2. 2 -4. 3 2 (-4) + (-4). (-1) 3 -1 3. 2 + (-1)3 3. (-4) +(-1) -8 -4 3 -11 ÇARPMA İŞLEMİNİN ÖZELLİKLERİ: A , B ve C matrislerinin birbirleriyle çarpımları tanımlı ve kЄR olsun. 1) (k. A). B = A. (k. B) =k. (A. B) 2) (A+B). C =A. C + B. C 3) C. (A+B) = C. A + C. B 4) A. (B. C) = (AB). C 5) 5) nxn türündeki In = 1 0 …. 0 1 …. 0 0 0 …. 1 0

(Köşegen üzerindeki elemanları 1, diğerleri 0 ‘dır. ) matrisi nxn türündeki matrislerde çarpma işleminin birim elemanıdır. Yani Anxn Inxn = Inxn A nxn = A nxn’dir. ÖRNEK : A= -1 3 ise; A 50 matrisini bulunuz. 0 1 A 2 = -1 3 0 1 = 1 0 = I 2 X 2 0 1 A 50 =(A 2 )25 = (I 2 X 2)25 = 1 0 olur. 01 ÖRNEK: A= -2 3 ise A 37 matrisini bulunuz. -1 2 A 2 = A. A = -2 3 -1 2 . -2 3 = 1 0 -1 2 0 1 = I 2 X 2

A 37 = (A 2)18. A = ( I 2 X 2)18. A = I 2 X 2. A = -2 3 -1 2 ÖRNEK: A= 1 2 ise A 30 matrisini bulunuz. 0 1 A 2 = 1 2 . 0 1 A 3 = 1 4 . 1 2 . A 30 = 1 2. 30 1 2 01 1 4 = 0 1 0 1 = 0 1 A 4 = 1 6 1 2 1 6 0 = 0 1 = 1 8 0 1 = 1 60 bulunur. 0 1 1 2. 2 1 1 2. 3 0 1 = 1 2. 4 0 1

BİR MATRİSİN DEVRİĞİ ( TRANSPOZU ) A = aij mxn matrisinin aynı indisli satırlarıyla sütunlarının yer değiştirmesiyle oluşturulan aji matrisine A matrisinin devriği denir ve AT ile ya da AD ile gösterilir. Örnek: 5 7 A = 0 -8 3 4 ise AT = 5 0 3 7 -8 4 ÖZELLİKLERİ: 1. A ve B mxn türünde iki matris ise (A+B)T = AT + BT 2. A bir matris kЄR ise (k. A)T = k AT 3. A, mxn türünde, B nxp türünde iki matris ise T (A. B) = BT. AT 4. (AT)T = A’ dır ÖRNEK: A = 2 3 -1 A. AT matrisini bulunuz. 4 0 5 ÇÖZÜM: nxm

2 4 AT = 3 0 ‘dir. -1 5 2 3 -1 2 4 A. AT = 4 0 5 3 0 -1 5 4+9+1 8+0 -5 16+0+25 = 14 3 3 41 ÖRNEK: A ve B iki matris olmak üzere A = B + B T ise AT matrisi nedir? A = (B+BT) ise AT = (B+BT)T = BT+ B = A bulunur.

DETERMİNANTLAR: TANIM : A bir kare matris olsun. A’nın determinantı deta ya da A ile gösterilir ve aşağıdaki şekilde tanımlanır. i. A = a 11 1 x 1 şeklinde bir matris ise; A = a 11 ii. iii. A = a 11 a 12 şeklinde bir matris ise; a 21 a 22 2 x 2 A = a 11. a 22 - a 12. a 21 A, nxn türünde bir matris olsun. A’nın i. Satırı ve j. Sütunu silinerek elde edilen matrisi Mij ile gösterelim. mij determinantına aij elemanının minörü, Aij = (-1) i+j Mij ‘ye aij’ nin eş çarpanı (kofaktörü) denir. Bir determinantın değeri herhangi bir satır (veya sütun) elemanları ile o satırdaki (veya sütundaki) elemanların kofaktörleri çarpımının toplamına eşittir. A = A 11 a 11+A 12 a 12+…+a 1 n. A 1 n (1. satıra göre açılımı) A = A 21 a 21 + A 22 a 22+…+a 2 n. A 2 n (2. satıra göre açılımı) A = A 11 a 11+a 21 A 21+a 31 A 31+…+am 1 Am 1 (1. sütuna göre)

iv. türündeki reel matrisler kümesinden R ye, A D fonksiyonuna determinant fonksiyonu denir. v. Örnek: vi. 5 =? -2 =? vii. 4 2 =? -3 4 7 8 viii. 5 = 5 -2 = -2 D(A)= A şeklinde tanımlanan =? 5 -8 4. 8 -2. 7=32 -14=18 -3. -8 – 4. 5 = 24 -20=4 ix. ÖRNEK: x. x-2 3 xi. x = 8 denklemini çözünüz. 5 xii. ÇÖZÜM: xiii. x-2 3 xiv. x xv. =8 5(x-2)-3 x = 8 5 5 x-10 -3 x = 8 2 x = 18 x=9 xvi. ÖRNEK: xvii. 5678 5679 xviii. 5676 5677 matrisinin determinantının değeri nedir?

A=5678 olsun. 5678 5679 = 5676 5677 a+2 a+3 a a+1 (a+1)(a+2)-a(a+3) A 2+3 a+2 -a 2 -3 a = 2 bulunur. A = 5 7 -8 matrisinin a 22 elemanı ile a 13 elemanının minörlerini yazınız. 2 0 4 6 9 3 ÇÖZÜM: A matrisinin 2. satır ve 2. sütun elemanlarının atılması ile elde edilen matrisin determinantı a 22 minörüdür. Buna göre 5 7 -8 2 0 4 6 9 3 M 22 = 5 -8 6 3 = 5. 3 -6 (-8) = 63

Aynı şekilde M 13 5 7 -8 = 2 0 2. 9 – 6. 0 = 18 6 9 2 0 4 6 9 3 =2. 9 -6. 0 = 18 bulunur. ÖRNEK: 3 2 4 A = -5 3 -2 matrisinin a 32 elemanına ait kofaktör (eş çarpan) nedir? 4 -3 5 ÇÖZÜM: 3 2 4 A 32 = (-1)3+2 M 32 = - 3 4 -5 3 -2 -5 -2 4 -3 5 = - (-6+20) = -14 SARRUS KURALI: a 11 a 12 a 13 A= a 21 a 22 a 23 a 31 a 32 a 33 matrisinin determinantı alt tarafa ilk iki satır yazılarak

ya da sağ tarafa ilk iki sütun yazılarak aşağıda gösterildigi şekilde hesaplanabilir. a 11 a 12 a 13 a 21 a 22 a 23 - a 31 a 32 a 33 + - a 11 a 12 a 13+ - a 21 a 22 a 23+ A = (a 11 a 22 a 33 + a 21 a 32 a 13 + a 31 a 12 a 23) -(a 13 a 22 a 31+a 23 a 32 a 11+a 33 a 12 a 21) a 11 a 12 a 13 a 11 a 12 a 21 a 22 a 23 a 21 a 22 - a 31 a 32 a 33 a 31 a 32 + - - + + A = (a 11 a 22 a 33 +a 12 a 23 a 31+a 13 a 21 a 32) -(a 13 a 22 a 31 +a 11 a 23 a 32 +a 12 a 21 a 33)

NOT : Sarrus kuralı yalnız 3 x 3 türündeki matrislerin determinantları hesaplanırken kullanılır. ÖRNEK: 3 2 5 A= 0 -4 1 matrisinin determinantını bulunuz. 2 3 4 ÇÖZÜM: 3 2 5 0 -4 1 - 2 3 4 + - 3 2 5 + - 0 -4 1 + A = 3(-4). 4 + 0. 3. 5 +2. 2. 1 - 5 (-4). 2 + 1. 3. 3+4. 2. 0 = (-48+4) – (-40+ 9) = -44 + 31 = -13 bulunur.

DETERMİNATIN ÖZELLİKLERİ: 1. Bir determinantın bir satırındaki ya da bir sütunundaki terimlerin türü 0 ise determinantın değeri 0 dır. 2. 4 3 7 3 0 2 3. 0 0 0 = 0, 1 0 -7 4. 5 2 8 3 0 5 =0 2. Bir determinantın iki satırındaki ya da iki sütunundaki terimler orantılı ise determinantın değeri 0 dır. Örneğin, 3. 2 3 4 4. 0 1 -2 5. 4 6 8 determinantında 1. satır ile 6. 3. satır ( 2/4= 3/6=4/8=1/2) orantılı olduğundan determinant 0 a eşittir. 3. Bir determinantın bir köşegeninin üstündeki ya da altındaki tüm elemanlar 0 ise determinant köşegen üzerindekielemanların çarpımına ya da çarpımın ters işaretlisine eşittir. Örneğin , 4.

3 4 2 0 3 1 0 0 5 2 1 3 4 2 0 1 0 0 = = 3 0 0 4 3 0 2 1 5 2 4 1 1 2 0 3 0 0 = 3. 3. 5 =45 = -( 3. 2. 1) = -6 4. Bir determinantın iki satırı ya ada iki sütunu yer değiştirirse determinant işaret değiştirir. Örneğin, a 1 a 2 a 3 a 2 a 1 a 3 b 1 b 2 b 3 = b 2 b 1 b 3 ‘tür. c 1 c 2 c 3 c 2 c 1 c 3 5. Bir determinantın bir satırı ya da sütunu bir k sayısı ile çarpılırsa determinant k ile çarpılmış olur. a 1 a 2 a 3 ka 1 ka 2 ka 3 b 1 b 2 b 3 = m ise b 1 b 2 b 3 = km olur. c 1 c 2 c 3 SONUÇ: A, nxn türünde bir matris ve k Є R ise k. A = kn A 6. Bir determinantın herhangi bir satırı ( veya sütunu) bir sayı ile çarpılıp diğer bir satıra (veya sütuna ) karşılıklı olarak eklenirse determinantın değeri değişmez. Örneğin,

Örneğin, a 1 a 2 a 3 a 1+kb 1 a 2+kb 2 a 3+kb 3 b 1 b 2 b 3 = b 1 b 2 b 3 c 1 c 2 c 3 7. A ve B nxn türünde iki matris ise A. B = A. B ve An = A n 8. A = AT ‘dir. 9. Bir determinanta bir satırın elemanları başka bir satırın elemanlarının eş çarpanları ile karşılıklı olarak çarpılır ve toplanırsa bu toplam 0 olur. (aynı özellik sütun için de doğrudur. ) Örneğin, a 11 a 12 a 13 10. A= a 22 a 23 ise a 11 A 31 +a 12 A 32 +a 13 A 33 = 0 dır. a 33 a 32 a 33 a 1+x b 1+y c 1+z a 2 b 2 c 2 a 3 b 3 c 3 a 1 b 1 c 1 x y z a 2 b 2 c 2 + a 2 b 2 c 2 dır. a 3 b 3 c 3 (aynı özellik sütünlar içinde geçerlidir. )

ÖRNEK: 2 1 0 4 2 3 1 -2 = A ise 5 4 -1 0 6 2 -4 determinantının değeri kaçtır. 10 8 -2 ÇÖZÜM: Bir determinantın bir satırı 2 ile çarpılırsa determinant 2 ile çarpılmış olur. Bu determinantın her satırı 2 ile çarpıldığına göre determinant 2. 2. 2 = 8 ile çarpılmış olur. ÖRNEK: A= 2 5 3 olduğuna göre A 4 matrisinin determinantı kaçtır. 7 ÇÖZÜM: A = 2 5 = 14 -15 = -1 3 7 A 4 = (-1)4 = 1

EK ( ADJOİNT) MATRİS: Karesel A matrisinin aij terimlerinin yerine Aij eş çarpanlarının yazılmasıyla oluşan Aij matrisinin devriğine A matrisinin ek matrisi denir ve Ek (A) ile gösterililr. ÖRNEK: 3 4 A= 2 0 5 -1 2 3 matrisinin ek matrisini bulunuz. 7 ÇÖZÜM: A 11 = (-1)1+1 5 -1 3 A 12 = (-1)1+2 = 35+3 = 38 7 0 -1 = - (0+2) = -2 2 7 A 13 = (-1)1+3 0 5 = 0 -10 =-10 2 3 A 21 = (-1)2+1 4 2 = -(28 -6) = -22
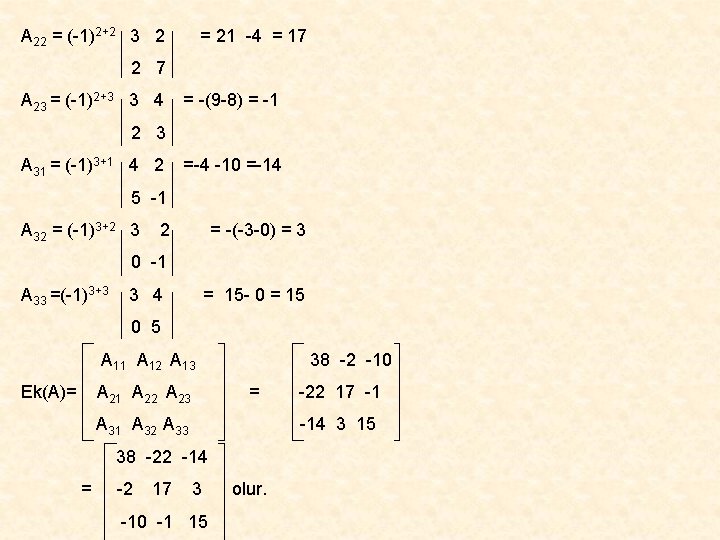
A 22 = (-1)2+2 3 2 = 21 -4 = 17 2 7 A 23 = (-1)2+3 3 4 = -(9 -8) = -1 2 3 A 31 = (-1)3+1 4 2 =-4 -10 =-14 5 -1 A 32 = (-1)3+2 3 2 = -(-3 -0) = 3 0 -1 A 33 =(-1)3+3 3 4 = 15 - 0 = 15 0 5 A 11 A 12 A 13 Ek(A)= A 21 A 22 A 23 38 -2 -10 = A 31 A 32 A 33 -14 3 15 38 -22 -14 = -2 17 -22 17 -1 3 -10 -1 15 olur.

BİR MATRİSİN ÇARPMA İŞLEMİNE GÖRE TERSİ: mxn türünden bir matris A olsun. A. B=B. A = In koşulunu sağlayan nxn türünde bir B matris varsa , B matrisine A nın çarpma işlemine göre tersi denir ve B = A-1 ile gösterilir. A. A-1 = A-1. A = I dır. ÖZELLİKLER: 1. A ≠ 0 ise A-1= 1/ A Ek (A) 2. A (Ek. A) =(Ek. A). A = A In 3. A-1 = 1/ A 4. (A-1) -1 = A 5. (AT) -1 = (A -1 )T 6. (AB) -1= B-1. A-1 7. NOT : 1. Bir A kare matrisini tersinin olabilmesi için A ≠ 0 olmalıdır. 2. Bir A kare matrisinin tersi (varsa ) tektir. 3. A kare matris ve A ≠ 0 ise A matrisine regular (tekli olmayan ) matris denir. A = 0 ise A matrisine singuler (tekil ) matris denir.

ÖRNEK: A= 2 3 matrisinin çarpma işlemine göre tersini bulunuz. -1 -2 ÇÖZÜM: A-1 = a b olsun. A. A -1 = I olması gerekir. c d 2 3 . -1 -2 a b = 1 0 c d 0 1 ise 2 a+3 c 2 b+3 d -a-2 c -b-2 d = 1 0 0 1 İse 2 a+3 c =1 2 b+3 d =0 -a-2 c = 0 -b -2 d =1 2 a+3 c= 1 2 b+3 d =0 + -2 a-4 c=0 -c=1 , c=-1 , a=2 + -2 b-4 d =2 -d=2 , d=-2, b= 3 A -1 = 2 3 -1 -2

BİR MATRİSİN RANKI: A, mxn tüünde bir matris olsun. A nın determinantları sıfırdan farklı olan kare matrislerden en büyük mertebeli olanın mertebesine , A nın rankı denir ve rank A ile gösterilir. ÖRNEK: 3 4 A= 5 6 matrisinin 2 x 2 türündeki bütün kare alt matrislerini yazınız. 0 2 ÇÖZÜM: 3 4 5 6 0 2 ÖRNEK: 3 4 2 0 5 -2 matrisinin rankını bulunuz.

A matrisi 3 x 2 türünden olduğundan A nın karesel alt matrisleri en çok 2 x 2 türünden olabilir. Bu nedenle rank(A) en fazla 2 olabilir. 2 x 2 boyutlu 3 4 2 0 Alt matrisinin determinantı 3 4 2 = 0 -8 =-8 ≠ 0 olduğundan rank(A)= 2 dir. 0 LİNEER DENKLEM SİSTAMLERİ: Bilimeyen x 1, x 2, …xn ve katsayıları gerçel sayılar olan , a 11 x 1 + a 12 x 2 +…a 1 nxn = b 1 A 21 x 1 + a 22 x 2 +…a 20 nxn = b 2 ……………. am 1 x 1 + am 2 x 2 +…amnxn =bm Denklemlerinden oluşşan sisteme n bilinmeyen lineer denklem sistemi denir. Matrislerde çarpma işleminin tanımından , a 11 a 12 … a 1 n a 21 a 22. . . a 2 n am 1 am 2 … amn x 1 x= x 2 xn

b 1 B= b 2 olmak üzere bm Yukarıdaki sistem A. X = B şeklinde yazılabilir. Burada A ya katsayılar matrisi denir. m = n ise A bir kare matris olur. . Bu durumda A -1 varsa, AX = B ise A -1. (A. X) =A -1. B ise (A -1)X =A -1. B ise In. X = A-1. B ise X=A -1. B bulunur. ÖRNEK: 3 x+2 y-z = 5 X-3 y+2 z = 6 denklem sistemini matrisler yardımıyla çözünüz.

ÇÖZÜM: x Katsayılar matrisi A = 3 2 -1 bilinmeyeler matrisi X = 1 -3 2 Ve sabit terimler matrisi B = 5 y z olsun. Buna göre verilen sistemler A. X=B ya 6 da 3 2 -1 x 1 -3 2. y 5 = 6 z Biçiminde yazılır. GRAMER KURALI: Bilinmeyen sayısı ile denklem sayısısnın eşit olduğu lineer denklem sistemlerinin pratik çözümlerini veren gramer kuralını inceleyelim. a 11 a 12. . A 1 n a 21 a 22 …a 2 n an 1 an 2 …ann dir.

1. ∆ ≠ 0 ise tek çözüm vardır. x 1 = ∆1 / x 2 = ∆2 / ∆ , … Xn = ∆n / ∆ dır. 2. ∆ = 0 ve ∆∆1, ∆2, …= ∆n lerden en az biri sıfırdan farklı ise sistemin çözümü yoktur. 3. ∆ = ∆1 = ∆2 … = ∆n = 0 ise sistemi sonsuz çözümü vardır. 4. ÖRNEK: 5. 3 x-2 y = 5 sisteminin çözümünü bulunuz. 6. 2 x +5 y = 1 7. ÇÖZÜM: 8. ∆ = 3 -2 = 15 - (-4) =19 9. 2 5

∆1 = 5 -2 = 25 – (-4) =19 1 5 ∆2 = 3 5 = 3 -10 = -7 2 1 X= ∆1/ ∆= 27/19 ve y = ∆2 / ∆ = -7/19 bulunur.
 Total set awareness set consideration set
Total set awareness set consideration set Training set validation set test set
Training set validation set test set üçüncül kaynak nedir
üçüncül kaynak nedir Hukuk yardımcı kaynaklar
Hukuk yardımcı kaynaklar Vergi hukuku asli kaynaklar
Vergi hukuku asli kaynaklar Maddi kaynaklar
Maddi kaynaklar Sınırlı kaynaklar ve teknoloji düzeyi eğrisi
Sınırlı kaynaklar ve teknoloji düzeyi eğrisi Www.nedir.org
Www.nedir.org Iş hukukunun kaynakları
Iş hukukunun kaynakları 3 kısa vadeli yabancı kaynaklar
3 kısa vadeli yabancı kaynaklar Hesap makinesi
Hesap makinesi Tali kaynaklar
Tali kaynaklar Asli kaynaklar
Asli kaynaklar Sınırlı kaynaklar ve teknoloji düzeyi eğrisi
Sınırlı kaynaklar ve teknoloji düzeyi eğrisi Personel bulmada kullanılan işletme dışı kaynaklar
Personel bulmada kullanılan işletme dışı kaynaklar Devin dahl
Devin dahl Devin vrana
Devin vrana Timmy turner on drugs
Timmy turner on drugs Spanish love words
Spanish love words Devin rouse
Devin rouse Devin schultz
Devin schultz Devin hudson
Devin hudson Devin knight power bi
Devin knight power bi Timothy leary marianne busch
Timothy leary marianne busch Devin trejo
Devin trejo Sevinli saldırganlık
Sevinli saldırganlık Cennetin krallığı konusu
Cennetin krallığı konusu Sunum konusu
Sunum konusu Anket türleri
Anket türleri Sunum konusu
Sunum konusu Doğru yoldan gidenler şaşırmazlar konusu
Doğru yoldan gidenler şaşırmazlar konusu Matris konusu
Matris konusu Fıkhi mezhepler
Fıkhi mezhepler