Development of a fuzzy logic Xband hydrometeor identification

Development of a fuzzy logic X-band hydrometeor identification algorithm Brenda Dolan and Steven Rutledge Colorado State University September 18, 2006 European Radar Conference

Road Map Motivation and Background u Methodology • Simulations using T-matrix and Mueller matrix u Results u Future work u

Introduction Collaborative Adaptive Sensing of the Atmosphere (CASA) Integrated project (IP 1) u • Network of 4 polarimetric Xband radars located in Oklahoma u Analyze the microphysical and kinematic structure of storms observed by the CASA IP 1 network • Dual-Doppler analysis • Polarimetric analysis Hydrometeor ID (HID) u Rain rate /snowfall estimation u

Introduction Why is radar identification of hydrometeors important? u • Identify regions of mixed phase • Determine possible regions of freezing rain and sleet • Use to drive rainrate and snowfall algorithms • Identify locations of possible ice contamination • Distinguish between aggregates and ice crystals • Locate large hail • Help validate numerical models Dolan and Rutledge, 2006

S-band vs. X-band u Extensive research and algorithm development at S-band (Straka et al. 2000, Liu and Chandrasekar 2001, Tessendorf et al. 2005) • Include observational data • Extending into C-band u u Little work has been done on HID algorithms for X-band Why do we expect the HID algorithm for X-band S-band to be different? • • Mie scattering Resonance Attenuation Kdp proportional to 1/ (Bringi and Chandrasekar 2001, Matrosov et al. 2006)

Fuzzy Logic n n One approach to HID is using fuzzy logic Combine information from polarimetric variables, as well as temperature n n Zh, Zdr, Kdp, hv in this case (no Ldr) Soft boundaries and ranges for each of the variables Variables can be weighted Each hydrometeor type is given a score based on how well the variables fit into the fuzzy set n Hydrometeor with highest score is considered the hydrometeor type at that data point

Fuzzy Logic: Membership Beta Functions (MBFs) Zh Zdr Kdp a m LDR Zh ρhv T These MBFs are from Tessendorf et al. (2005) for S-band b

Hydrometeor Types u We are interested in distinguishing the following precipitation types: • • • Rain Drizzle Wet (low-density) graupel Dry (high-density) graupel Snow (wet) Snow (dry) Pristine ice crystals (dendrites/columns) Vertically aligned ice crystals Hail (added complications)

Methodology u Determine the “most probable” ranges of variables at X-band • Thus determining m (midpoint) and a (width) of MBF • Using T-matrix and Mueller Matrix (Barber and Yeh 1975, Vivekanandan et al. 1991) scattering models to simulate a variety of precipitation events u u Provides simulated radar data Assign a “confidence” to the determined ranges => b (MBF slope) • As the algorithm is tested, modify these to become “more confident” about data ranges u Run simulations for both X and S-band (for comparison with literature)

Methodology: T-matrix u T-matrix: Simulates the scattering properties of a single particle • Can change: Radar wavelength (3. 2 cm, 11. 0 cm) u Particle input sizes (rain: 0. 05 cm to 1. 0 cm, drizzle: 0. 1 cm 0. 6 cm) u Temperature (-10, 0, 10, 20 ºC) u Size-Axis ratio relationship (Goddard and Cherry, 1984) u Dielectric constant u u u Follow parameters for different hydrometeors outlined in Straka et al. (2000) Run the model changing a single parameter at a time

Methodology: Mueller Matrix u Mueller Matrix: Generates the radar observables for a simulated “radar volume” • Can change Radar elevation angle (1. 0, 30. 0º) u Drop size distribution (DSD) (Do, No) u Canting angles (distribution and std dev) (0 -10º) u Range of particle diameters to use u • Base the parameters on Straka et al. (2000)

Methodology: Mueller Matrix u u Run the model for a wide variety of DSDs Use Marshall Palmer for rain • • • u N(D)=N 0 exp- D Fix No at 80, 000 m 3 cm-1 Vary as a function of rain rate -0. 21 u =4. 1 R • R=1 -200 mm hr-1 for rain u And assume: • Do=3. 67 / Use monodisperse DSD for drizzle • R=0. 1 - 2 mm hr-1

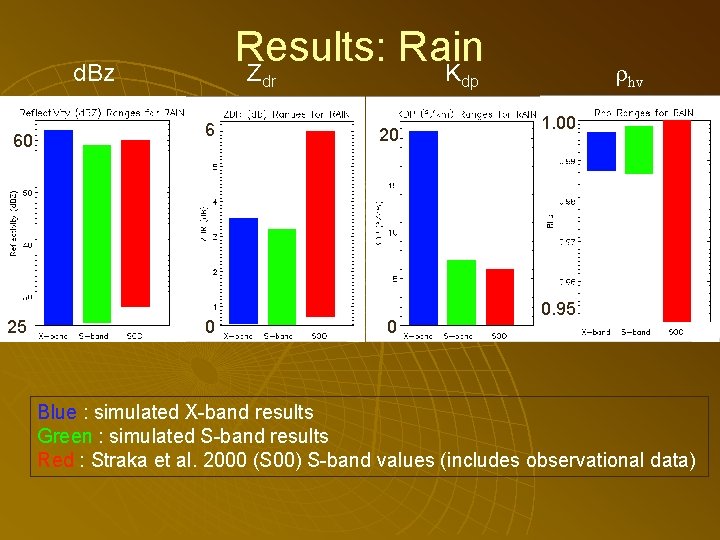
Results: Rain Z K d. Bz 60 25 dr 6 0 hv dp 20 0 1. 00 0. 95 Blue : simulated X-band results Green : simulated S-band results Red : Straka et al. 2000 (S 00) S-band values (includes observational data)

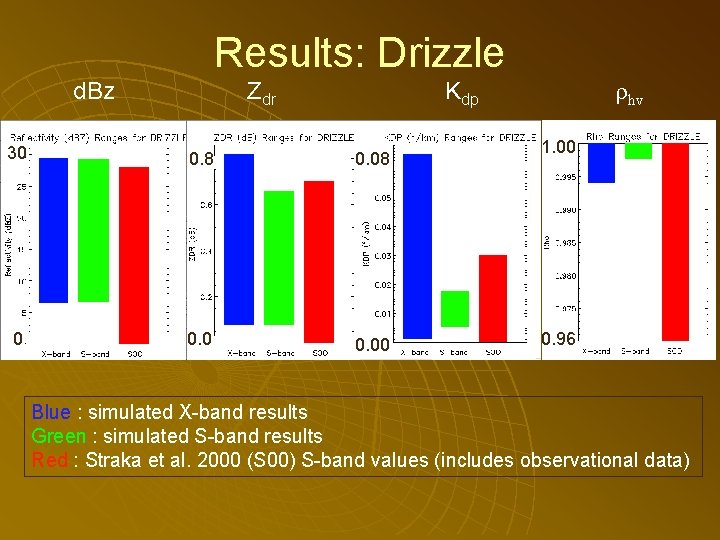
Results: Drizzle d. Bz Zdr hv Kdp 30 0. 8 0. 0 0 0. 00 1. 00 0. 96 Blue : simulated X-band results Green : simulated S-band results Red : Straka et al. 2000 (S 00) S-band values (includes observational data)

Results: Key differences between S-band X-band u For rain: Variables seem to be a bit higher at X-band over S-band • Especially Kdp We expect this with wavelength scaling u u For drizzle: Zdr and Kdp were higher for X- band over S-band

Future work u u Resolve differences between S-band simulations and observations Run simulations for • • u Rain (using Gamma distribution) Graupel Sleet Different ice crystals and snow types Test new X-band HID against S-band using observations • GPM Front Range Pilot Project u Implement in CASA radar network • Inter-compare with KOUN

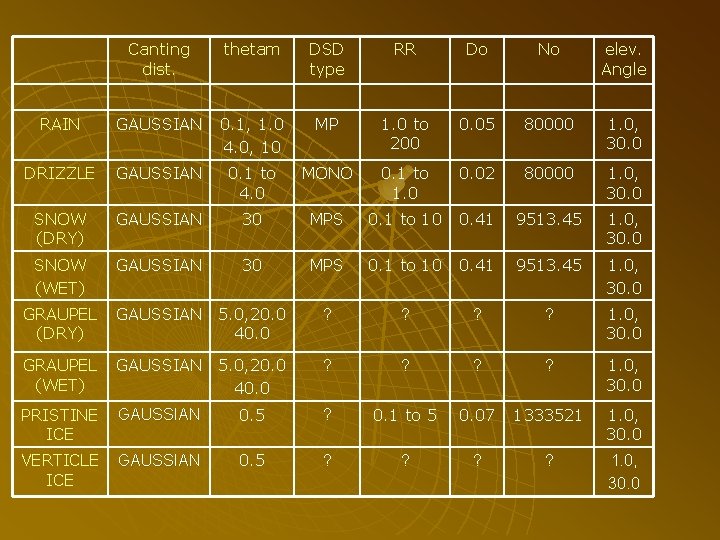
Canting dist. thetam DSD type RR Do No elev. Angle RAIN GAUSSIAN 0. 1, 1. 0 4. 0, 10 MP 1. 0 to 200 0. 05 80000 1. 0, 30. 0 DRIZZLE GAUSSIAN 0. 1 to 4. 0 MONO 0. 1 to 1. 0 0. 02 80000 1. 0, 30. 0 SNOW (DRY) GAUSSIAN 30 MPS 0. 1 to 10 0. 41 9513. 45 1. 0, 30. 0 SNOW (WET) GAUSSIAN 30 MPS 0. 1 to 10 0. 41 9513. 45 1. 0, 30. 0 GRAUPEL (DRY) GAUSSIAN 5. 0, 20. 0 40. 0 ? ? 1. 0, 30. 0 GRAUPEL (WET) GAUSSIAN 5. 0, 20. 0 40. 0 ? ? 1. 0, 30. 0 PRISTINE ICE GAUSSIAN 0. 5 ? 0. 1 to 5 0. 07 1333521 1. 0, 30. 0 VERTICLE ICE GAUSSIAN 0. 5 ? ? 1. 0, 30. 0

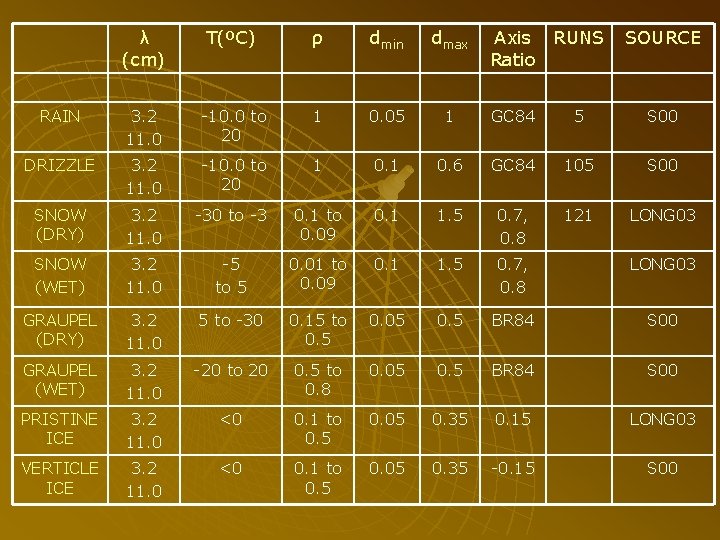
λ (cm) T(ºC) ρ dmin dmax Axis RUNS Ratio SOURCE RAIN 3. 2 11. 0 -10. 0 to 20 1 0. 05 1 GC 84 5 S 00 DRIZZLE 3. 2 11. 0 -10. 0 to 20 1 0. 6 GC 84 105 S 00 SNOW (DRY) 3. 2 11. 0 -30 to -3 0. 1 to 0. 09 0. 1 1. 5 0. 7, 0. 8 121 LONG 03 SNOW (WET) 3. 2 11. 0 -5 to 5 0. 01 to 0. 09 0. 1 1. 5 0. 7, 0. 8 LONG 03 GRAUPEL (DRY) 3. 2 11. 0 5 to -30 0. 15 to 0. 5 0. 05 0. 5 BR 84 S 00 GRAUPEL (WET) 3. 2 11. 0 -20 to 20 0. 5 to 0. 8 0. 05 0. 5 BR 84 S 00 PRISTINE ICE 3. 2 11. 0 <0 0. 1 to 0. 5 0. 05 0. 35 0. 15 LONG 03 VERTICLE ICE 3. 2 11. 0 <0 0. 1 to 0. 5 0. 05 0. 35 -0. 15 S 00

Results RAIN db. Z ZDR (d. B) KDP (º/km) Rho T (ºC) X-band 25 -62 0. 03 -3. 9 0 -22 0. 980 -0. 999 >-15 S-band 25 -59 0. 3 -3. 3 0 -7 0. 981 -0. 998 >-15 SMBF 22 -62 >0 0 -6 >0. 93 >-15 S 00 <60 >0 >0. 95 >0 >-10 X-band 7 -29 0. 1 -0. 8 0. 0 -0. 07 0. 994 -1. 0 >0 S-band 7 -29 0. 1 -0. 65 0. 001 -0. 017 0. 9975 -1. 0 >0 SMBF <30 0 -1 ~0 >0. 95 >0 S 00 28 -44 0. 7 -2. 0 0. 03 -0. 6 >0. 95 >0 X-band -35 to 25 0. 0 -0. 18 0. 0 -0. 010 1 <0 S-band - - <0 SMBF <40 >0 0 -1 <0. 93 <0 S 00 <35 0 -1 0 -0. 2 >0. 95 <0 DRIZZLE SNOW (DRY)