Development and Application of Composition Dependent Diffusion Databases

Development and Application of Composition. Dependent Diffusion Databases: Solid State Diffusion Carelyn E. Campbell National Institute of Standards and Technology Metallurgy Division Gaithersburg, MD 20899 Ø Motivation Ø Multicomponent Diffusion Basics Ø Development and Structure of a Diffusion Mobility Database Ø Validation of Database Ø Applications using Diffusion Mobility Databases Constructing Kinetic Databases April 20, 2004 This work was partially funded by the GE-led DARPA AIM program

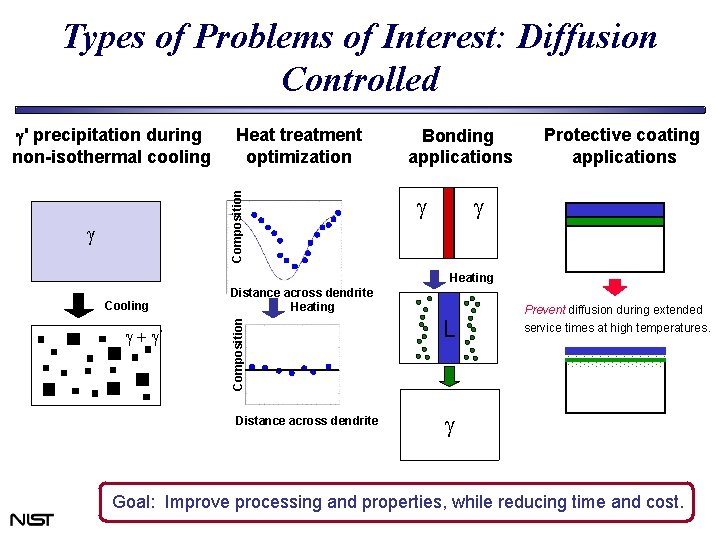
Types of Problems of Interest: Diffusion Controlled Heat treatment optimization Composition g' precipitation during non-isothermal cooling g Bonding applications g Protective coating applications g Heating g + g Distance across dendrite Heating Composition Cooling Distance across dendrite L Prevent diffusion during extended service times at high temperatures. g Goal: Improve processing and properties, while reducing time and cost.

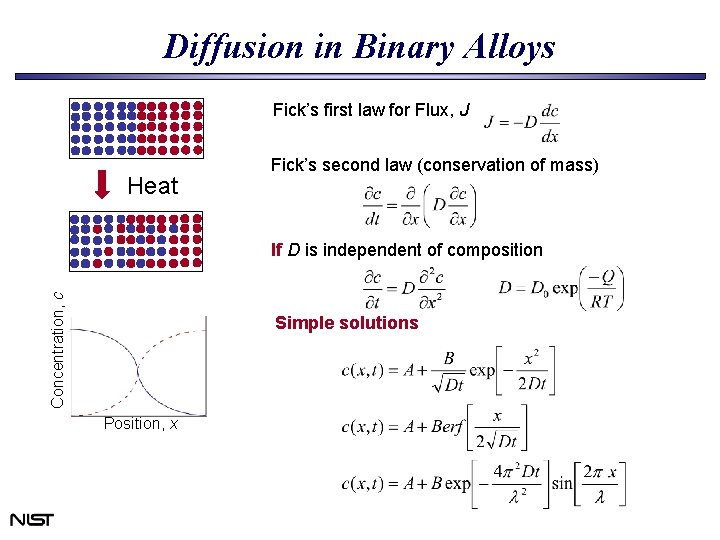
Diffusion in Binary Alloys Fick’s first law for Flux, J Heat Fick’s second law (conservation of mass) Concentration, c If D is independent of composition Simple solutions Position, x

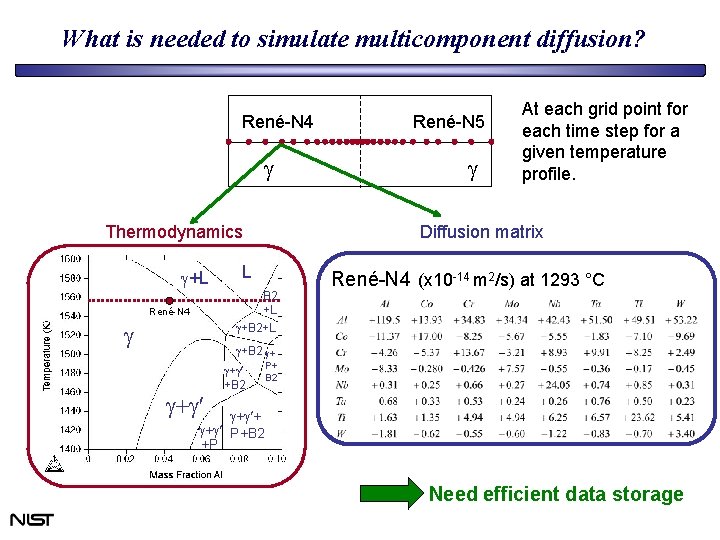
What is needed to simulate multicomponent diffusion? René-N 4 g Thermodynamics g+L g g At each grid point for each time step for a given temperature profile. Diffusion matrix L B 2 +L g+B 2+L René-N 4 René-N 5 René-N 4 (x 10 -14 m 2/s) at 1293 °C g+B 2 g+ g+g +B 2 P+ B 2 g+g + g+g P+B 2 +P Need efficient data storage

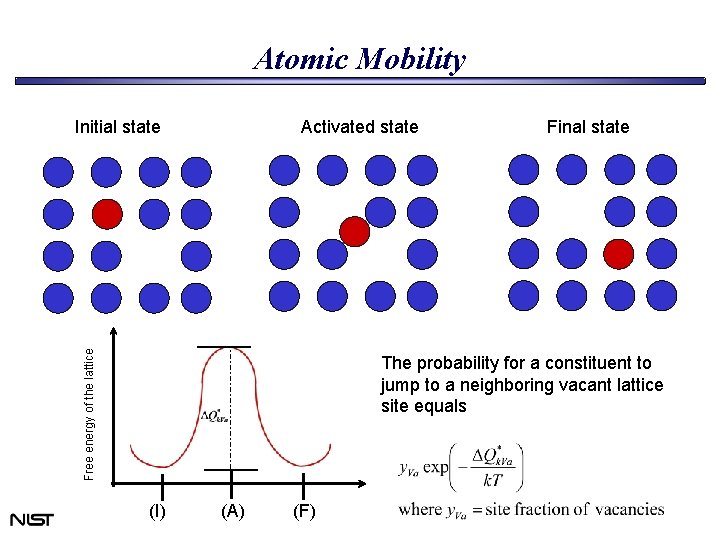
Atomic Mobility Initial state Free energy of the lattice Activated state Final state The probability for a constituent to jump to a neighboring vacant lattice site equals (I) (A) (F)

Diffusion in Multicomponent Solids To describe the flux of atoms in the presence of a driving force (composition gradient) and assuming the vacancy concentration is in thermodynamic equilibrium: Lattice fixed frame of reference Note: Tracer diffusivity is given by where and is not dependent on thermodynamics Volume fixed frame of reference where Chemical (interdiffusion coefficient) *References: Borgenstam et. al. , J. Phase Equilibria, 21 (2000) 269. Ågren, J. Phys. Chem. Solids, 43 (1982) 421. Andersson and Ågren, J. Appl. Phys. 72 (1992) 1350. Ågren, J. Phys. Chem. Solids, 43 (1982) 385.

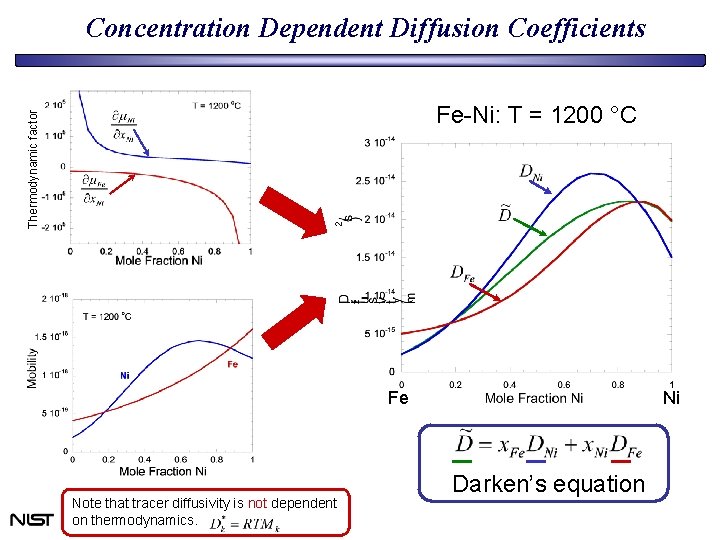
Concentration Dependent Diffusion Coefficients Thermodynamic factor Fe-Ni: T = 1200 °C Fe Note that tracer diffusivity is not dependent on thermodynamics. Ni Darken’s equation

Diffusion Database Development Ø Inputs: – Thermodynamics (CALPHAD approach) – Diffusion experiments (unary, binary, ternary systems) • Tracer diffusivity, • Intrinsic diffusivity, • Interdiffusion coefficients/Marker motion Ø Optimize value of mobilities, Mi , for all binaries consistent with available data – Composition and Temperature-dependent – Consistent with estimates of Metastable end members e. g. , FCC W – Optimized using code, DICTRA (Parrot) is exponentially dependent on composition and

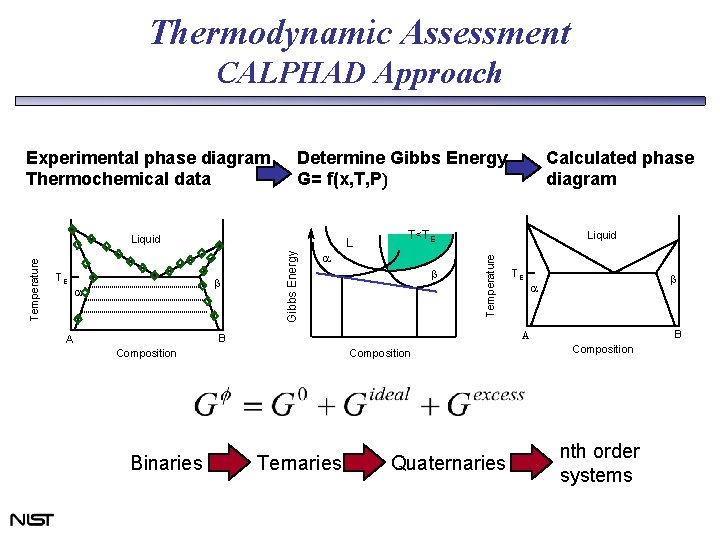
Thermodynamic Assessment CALPHAD Approach Determine Gibbs Energy G= f(x, T, P) TE L b a Gibbs Energy Temperature Liquid a b Liquid Composition Binaries TE b a B A Calculated phase diagram T<TE Temperature Experimental phase diagram Thermochemical data Ternaries Quaternaries Composition nth order systems

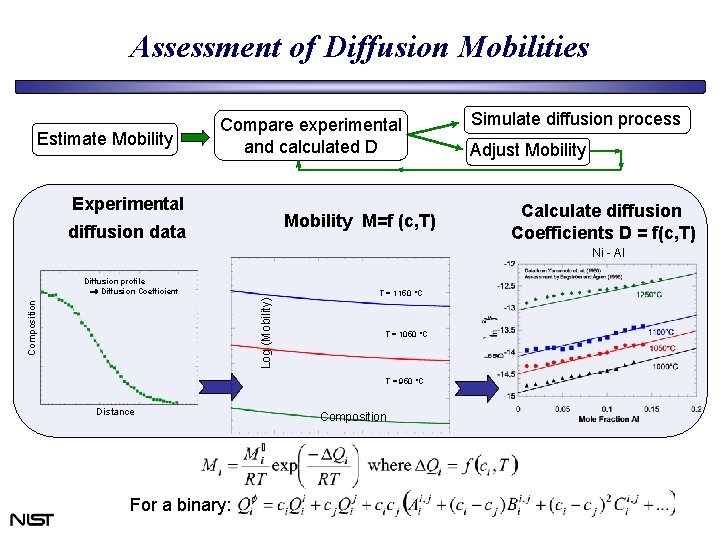
Assessment of Diffusion Mobilities Estimate Mobility Compare experimental and calculated D Experimental Mobility M=f (c, T) diffusion data Simulate diffusion process Adjust Mobility Calculate diffusion Coefficients D = f(c, T) Ni - Al Composition Log (Mobility) Diffusion profile Diffusion Coefficient T = 1150 °C T = 1050 °C T = 950 °C Distance For a binary: Composition

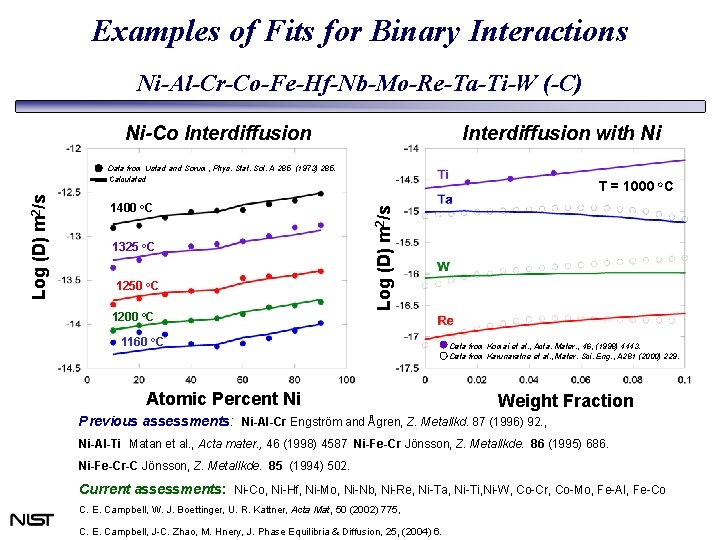
Examples of Fits for Binary Interactions Ni-Al-Cr-Co-Fe-Hf-Nb-Mo-Re-Ta-Ti-W (-C) Ni-Co Interdiffusion with Ni 1400 o. C 1325 o. C 1250 o. C 1200 o. C T = 1000 o. C Log (D) m 2/s Data from Ustad and Sorum, Phys. Stat. Sol. A 285 (1973) 285. Calculated 1160 o. C Atomic Percent Ni Data from Komai et al. , Acta. Mater. , 46, (1998) 4443. Data from Karunaratne et al. , Mater. Sci. Eng. , A 281 (2000) 229. Weight Fraction Previous assessments: Ni-Al-Cr Engström and Ågren, Z. Metallkd. 87 (1996) 92. , Ni-Al-Ti Matan et al. , Acta mater. , 46 (1998) 4587 Ni-Fe-Cr Jönsson, Z. Metallkde. 86 (1995) 686. Ni-Fe-Cr-C Jönsson, Z. Metallkde. 85 (1994) 502. Current assessments: Ni-Co, Ni-Hf, Ni-Mo, Ni-Nb, Ni-Re, Ni-Ta, Ni-Ti, Ni-W, Co-Cr, Co-Mo, Fe-Al, Fe-Co C. E. Campbell, W. J. Boettinger, U. R. Kattner, Acta Mat, 50 (2002) 775, C. E. Campbell, J-C. Zhao, M. Hnery, J. Phase Equilibria & Diffusion, 25, (2004) 6.

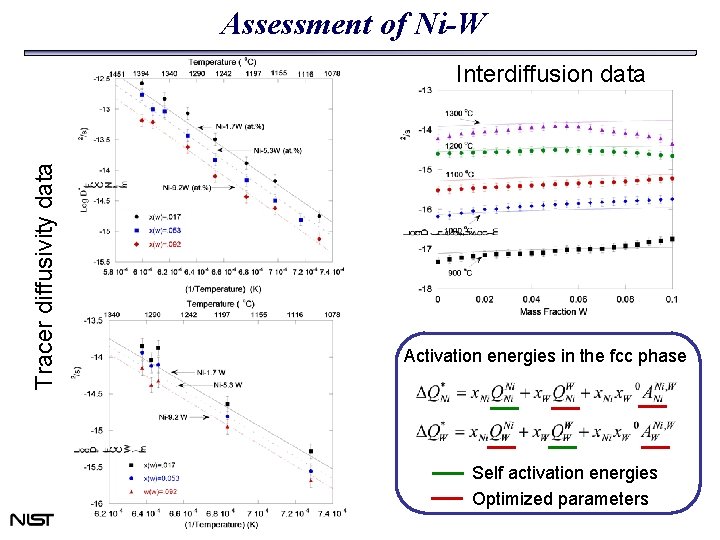
Assessment of Ni-W Tracer diffusivity data Interdiffusion data Activation energies in the fcc phase Self activation energies Optimized parameters

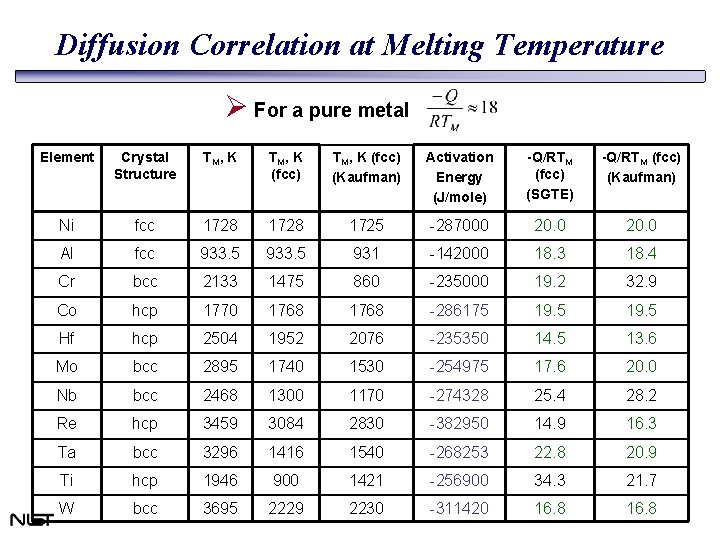
Diffusion Correlation at Melting Temperature Ø For a pure metal Element Crystal Structure TM , K (fcc) TM, K (fcc) (Kaufman) Activation Energy (J/mole) -Q/RTM (fcc) (SGTE) -Q/RTM (fcc) (Kaufman) Ni fcc 1728 1725 -287000 20. 0 Al fcc 933. 5 931 -142000 18. 3 18. 4 Cr bcc 2133 1475 860 -235000 19. 2 32. 9 Co hcp 1770 1768 -286175 19. 5 Hf hcp 2504 1952 2076 -235350 14. 5 13. 6 Mo bcc 2895 1740 1530 -254975 17. 6 20. 0 Nb bcc 2468 1300 1170 -274328 25. 4 28. 2 Re hcp 3459 3084 2830 -382950 14. 9 16. 3 Ta bcc 3296 1416 1540 -268253 22. 8 20. 9 Ti hcp 1946 900 1421 -256900 34. 3 21. 7 W bcc 3695 2229 2230 -311420 16. 8

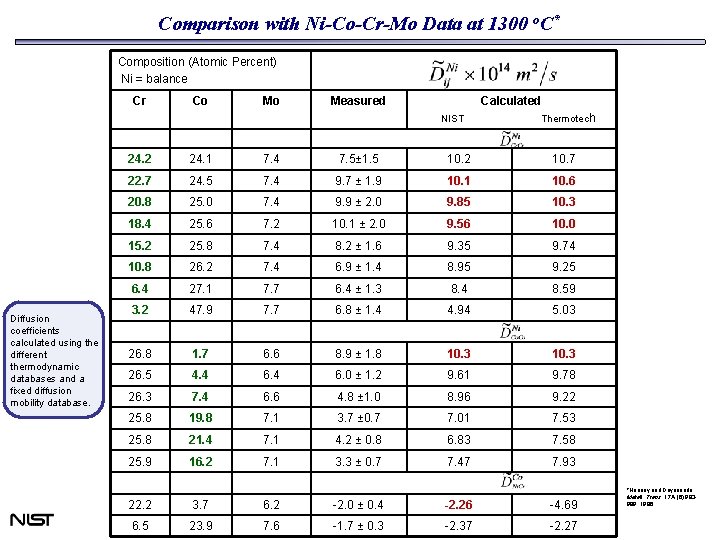
Comparison with Ni-Co-Cr-Mo Data at 1300 o. C* Composition (Atomic Percent) Ni = balance Cr Co Mo Measured Calculated NIST Diffusion coefficients calculated using the different thermodynamic databases and a fixed diffusion mobility database. Thermotech 24. 2 24. 1 7. 4 7. 5± 1. 5 10. 2 10. 7 22. 7 24. 5 7. 4 9. 7 ± 1. 9 10. 1 10. 6 20. 8 25. 0 7. 4 9. 9 ± 2. 0 9. 85 10. 3 18. 4 25. 6 7. 2 10. 1 ± 2. 0 9. 56 10. 0 15. 2 25. 8 7. 4 8. 2 ± 1. 6 9. 35 9. 74 10. 8 26. 2 7. 4 6. 9 ± 1. 4 8. 95 9. 25 6. 4 27. 1 7. 7 6. 4 ± 1. 3 8. 4 8. 59 3. 2 47. 9 7. 7 6. 8 ± 1. 4 4. 94 5. 03 26. 8 1. 7 6. 6 8. 9 ± 1. 8 10. 3 26. 5 4. 4 6. 0 ± 1. 2 9. 61 9. 78 26. 3 7. 4 6. 6 4. 8 ± 1. 0 8. 96 9. 22 25. 8 19. 8 7. 1 3. 7 ± 0. 7 7. 01 7. 53 25. 8 21. 4 7. 1 4. 2 ± 0. 8 6. 83 7. 58 25. 9 16. 2 7. 1 3. 3 ± 0. 7 7. 47 7. 93 22. 2 3. 7 6. 2 -2. 0 ± 0. 4 -2. 26 -4. 69 6. 5 23. 9 7. 6 -1. 7 ± 0. 3 -2. 37 -2. 27 *Heaney and Dayananda. Metall. Trans. 17 A (6): 983989, 1986.

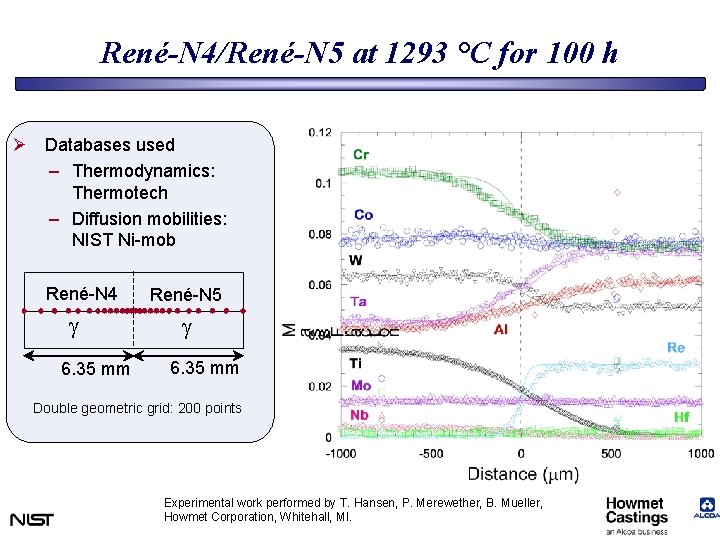
René-N 4/René-N 5 at 1293 °C for 100 h Ø Databases used – Thermodynamics: Thermotech – Diffusion mobilities: NIST Ni-mob René-N 4 g 6. 35 mm René-N 5 g 6. 35 mm Double geometric grid: 200 points Experimental work performed by T. Hansen, P. Merewether, B. Mueller, Howmet Corporation, Whitehall, MI.

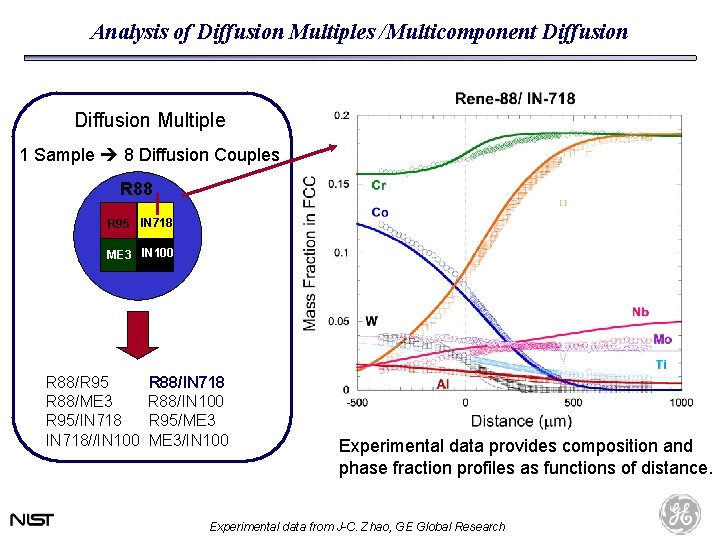
Analysis of Diffusion Multiples /Multicomponent Diffusion Multiple 1 Sample 8 Diffusion Couples R 88 R 95 IN 718 ME 3 IN 100 R 88/R 95 R 88/ME 3 R 95/IN 718//IN 100 R 88/IN 718 R 88/IN 100 R 95/ME 3/IN 100 Experimental data provides composition and phase fraction profiles as functions of distance. Experimental data from J-C. Zhao, GE Global Research

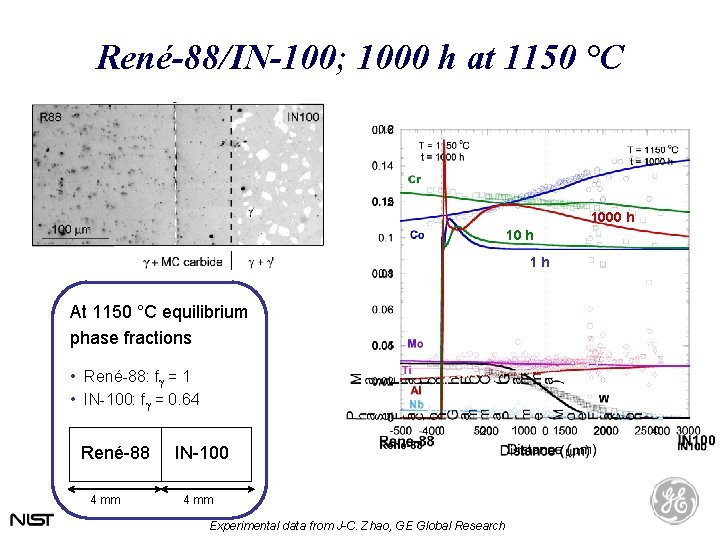
René-88/IN-100; 1000 h at 1150 °C 1000 h 1 h At 1150 °C equilibrium phase fractions • René-88: fg = 1 • IN-100: fg = 0. 64 René-88 4 mm IN-100 4 mm Experimental data from J-C. Zhao, GE Global Research

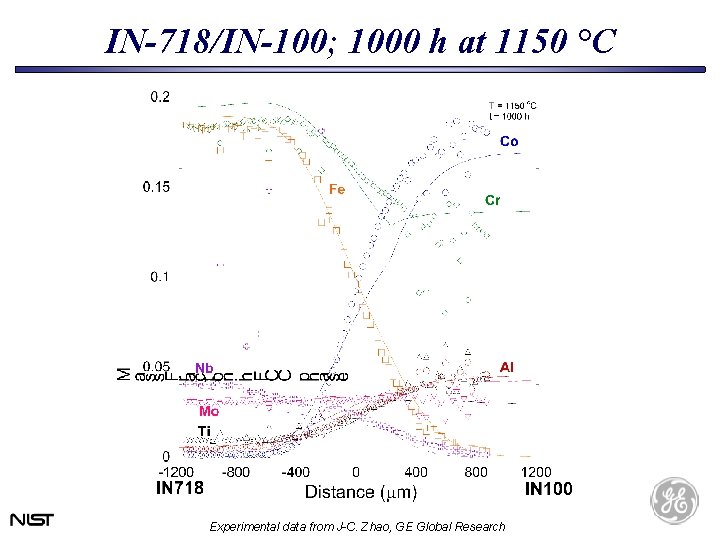
IN-718/IN-100; 1000 h at 1150 °C Experimental data from J-C. Zhao, GE Global Research

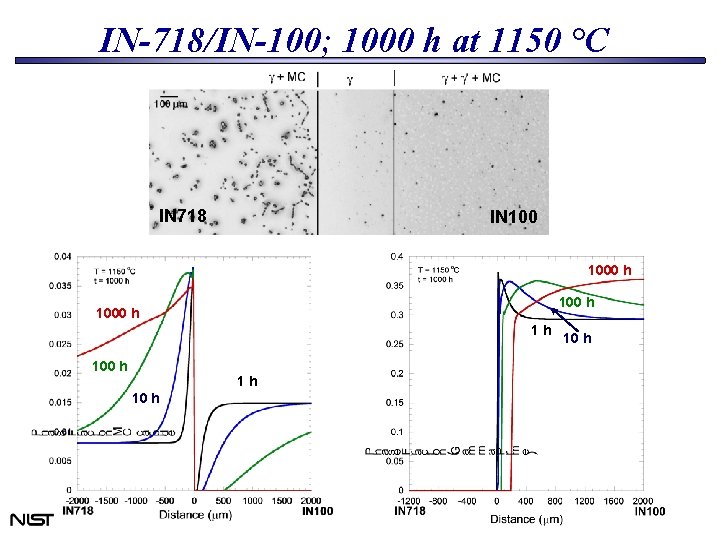
IN-718/IN-100; 1000 h at 1150 °C IN 718 IN 1000 h 1 h 10 h

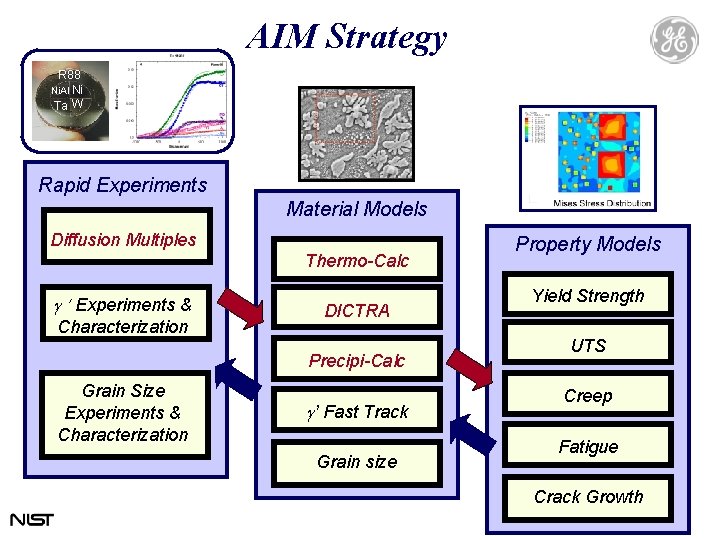
AIM Strategy R 88 Ni. Al Ni Ta W Rapid Experiments Material Models Diffusion Multiples Thermo-Calc g Experiments & Characterization DICTRA Precipi-Calc Grain Size Experiments & Characterization g’ Fast Track Grain size Property Models Yield Strength UTS Creep Fatigue Crack Growth

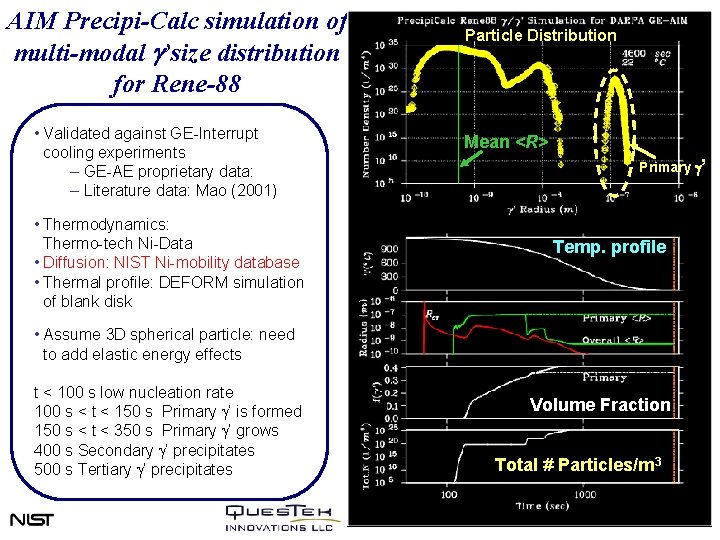
AIM Precipi-Calc simulation of multi-modal g’size distribution for Rene-88 • Validated against GE-Interrupt cooling experiments – GE-AE proprietary data: – Literature data: Mao (2001) • Thermodynamics: Thermo-tech Ni-Data • Diffusion: NIST Ni-mobility database • Thermal profile: DEFORM simulation of blank disk Particle Distribution Mean <R> Primary g’ Temp. profile • Assume 3 D spherical particle: need to add elastic energy effects t < 100 s low nucleation rate 100 s < t < 150 s Primary g’ is formed 150 s < t < 350 s Primary g’ grows 400 s Secondary g’ precipitates 500 s Tertiary g’ precipitates Volume Fraction Total # Particles/m 3

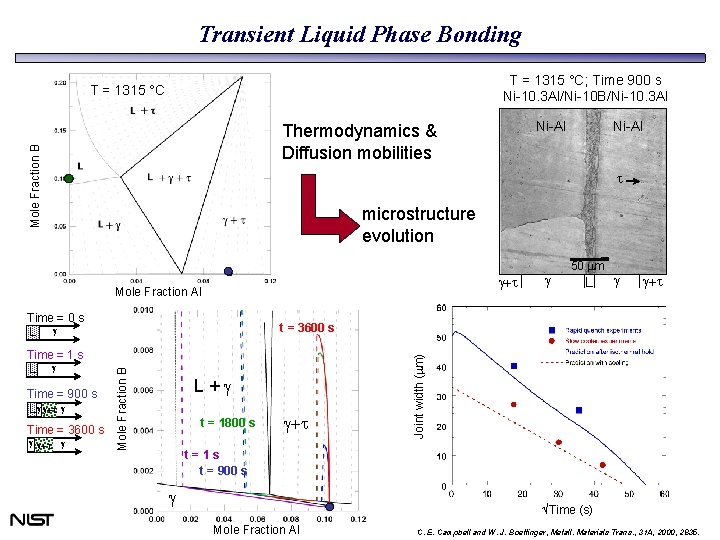
Transient Liquid Phase Bonding T = 1315 °C; Time 900 s Ni-10. 3 Al/Ni-10 B/Ni-10. 3 Al T = 1315 °C Mole Fraction B Ni-Al t microstructure evolution g+t Mole Fraction Al Time = 0 s L g Time = 3600 s g L g g+t L+g t = 1800 s g+t Joint width (mm) Time = 900 s L g g+t g g 50 mm t = 3600 s Mole Fraction B Time = 1 s L g g g+t Ni-Al Thermodynamics & Diffusion mobilities t=1 s t = 900 s g Time (s) Mole Fraction Al C. E. Campbell and W. J. Boettinger, Metall. Materials Trans. , 31 A, 2000, 2835.

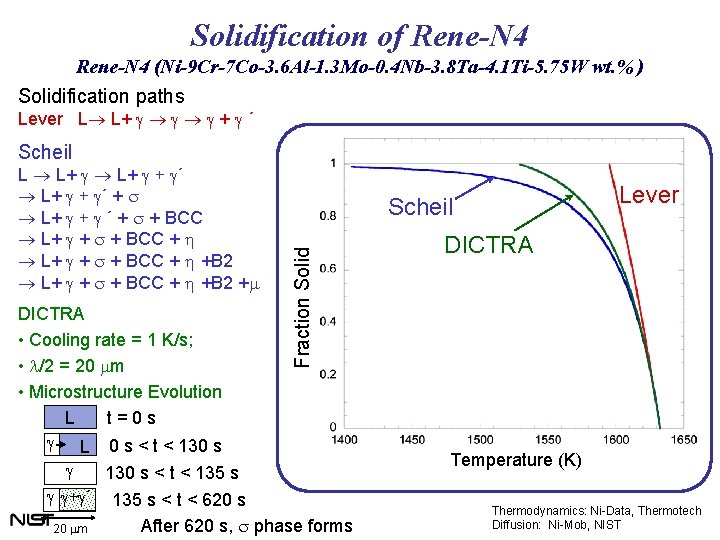
Solidification of Rene-N 4 (Ni-9 Cr-7 Co-3. 6 Al-1. 3 Mo-0. 4 Nb-3. 8 Ta-4. 1 Ti-5. 75 W wt. % ) Solidification paths Lever L L+ g g g + g ´ Scheil DICTRA • Cooling rate = 1 K/s; • l/2 = 20 mm • Microstructure Evolution L t=0 s g L 0 s < t < 130 s Lever Scheil Fraction Solid L L+ g + g´ + s L+ g ´ + s + BCC L+ g + s + BCC + h +B 2 +m g 130 s < t < 135 s g g+g´ 135 s < t < 620 s After 620 s, s phase forms 20 mm DICTRA Temperature (K) Thermodynamics: Ni-Data, Thermotech Diffusion: Ni-Mob, NIST

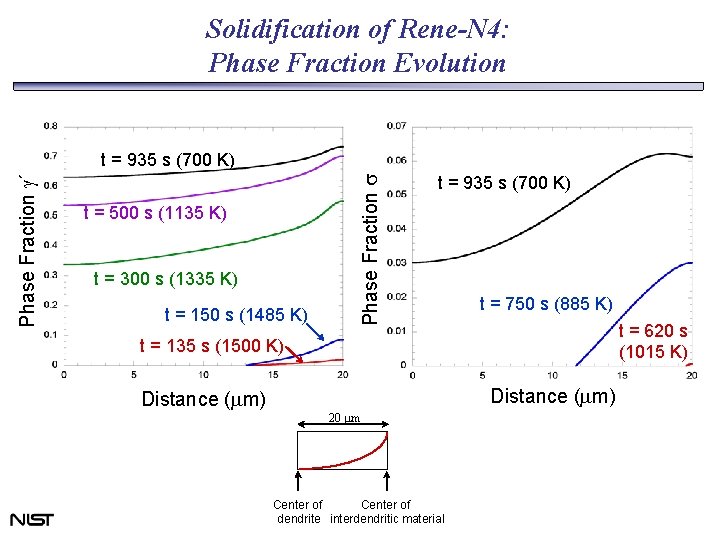
Solidification of Rene-N 4: Phase Fraction Evolution t = 500 s (1135 K) t = 300 s (1335 K) t = 150 s (1485 K) Phase Fraction s Phase Fraction g´ t = 935 s (700 K) t = 750 s (885 K) t = 620 s (1015 K) t = 135 s (1500 K) Distance (mm) 20 mm Center of dendrite interdendritic material

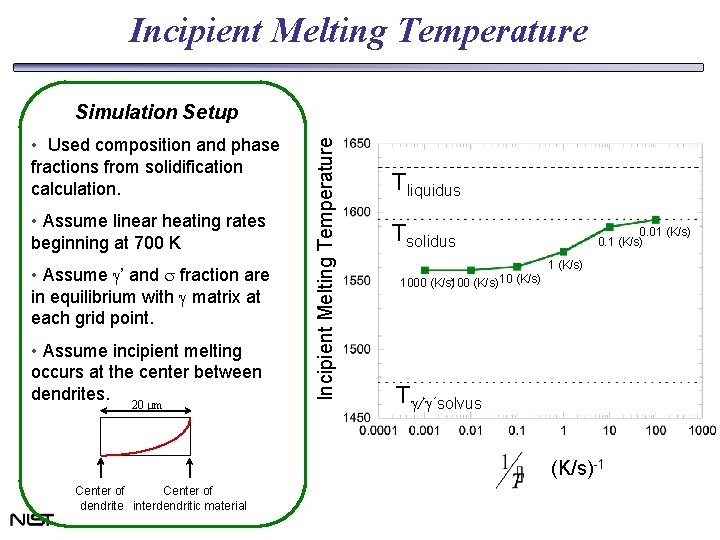
Incipient Melting Temperature • Used composition and phase fractions from solidification calculation. • Assume linear heating rates beginning at 700 K • Assume g’ and s fraction are in equilibrium with g matrix at each grid point. • Assume incipient melting occurs at the center between dendrites. 20 mm Incipient Melting Temperature Simulation Setup Tliquidus Tsolidus 0. 01 (K/s) 0. 1 (K/s) 1000 (K/s)100 (K/s) 10 (K/s) Tg/g´solvus (K/s)-1 Center of dendrite interdendritic material

Diffusion Database Center C. E. Campbell, U. R. Kattner, C. Beauchamp, K. Dotterer, H. Gates, S. Tobery, L. Souders c Goal: To make the NIST paper-based diffusion database center publicly available. Ø Convert to a searchable electronic form to be access over the internet v Motivation • Industrial and academic support: GE $5 K initiation • Center represents an unique collection summarizing the diffusion work between 1965 -1980 Ø Task: • Need to enter 25000 bibliographic and diffusion system cards • Convert paper documents to electronic documents • Develop searchable database ü Accomplishments • Developed database entry strategy • Entered bibliographic cards • Purchase high speed scanner and software

Other databases v TCS Alloy mobility database (v 2. 0, 1999). It is the most general alloy mobility database, within a framework of 75 elements. It can be used for steels/Fe-alloys, some Ni-based alloys, some Al-based alloys and more. v Bishop Dilute Al-alloy mobility database (v 1, 1995). It contains mobility data for dilute Al-based alloys, within a framework of 30 elements. v Oikawa Dilute Fe-alloy mobility database (v 1, 1995). It contains mobility data for dilute Fe-based alloys, within a framework of 28 elements. v Friberg Dilute Fe-alloy mobility database (v 1, 1995). It contains mobility data for dilute Fe-based alloys, within a framework of 16 elements. It can be used for dilute Fe-alloys. Available from Thermo. Calc Software AB

Summary/Future Work • Diffusion mobility databases Ø Based unary, binary, and ternary tracer, intrinsic, and chemical diffusivities Ø Dependent on available thermodynamic databases Ø Extrapolate to n-component systems Ø Need unstable end-members • NIST-Ni. MOB (Ni (fcc) diffusion mobility database ü FCC phase only ü 13 components (Ni-rich alloys) • Applications (Ni-base superalloys, steels, Al alloys, solders) §Transient Liquid Phase Bonding § Heat Treatment Optimization § Solidification • Future Work Ø Diffusion order phases Ø Optimization of mobility parameters directly from experimental data Ø Charged ions: Oxide phases (Höglund Thermo-Calc Software AB) Ø Atomistic and first principle calculations of unstable phases Ø Lateral Deformation of Diffusion Couples (3 -D Kirkendall effect (Boettinger, NIST) Ø High Throughput Analysis of Multicomponent Multiphase Diffusion Data working group (www. ctcms. nist. gov/~cecamp/workshop. html)

Diffusion in Ordered Phases • Expansion to Multicomponent systems Helander and Ågren, (Acta Mater. , 1999, 47, 1141. ) DQ = DQdis + DQord = contribution to activation energy for component k as a result of the ordering of i-j atoms Interdiffusion Coefficient (cm 2/s) Ni. Al-B 2 Atomic percent Al From Shankar and Seigle, Metall. Trans. 9 A, (1978) 1476.

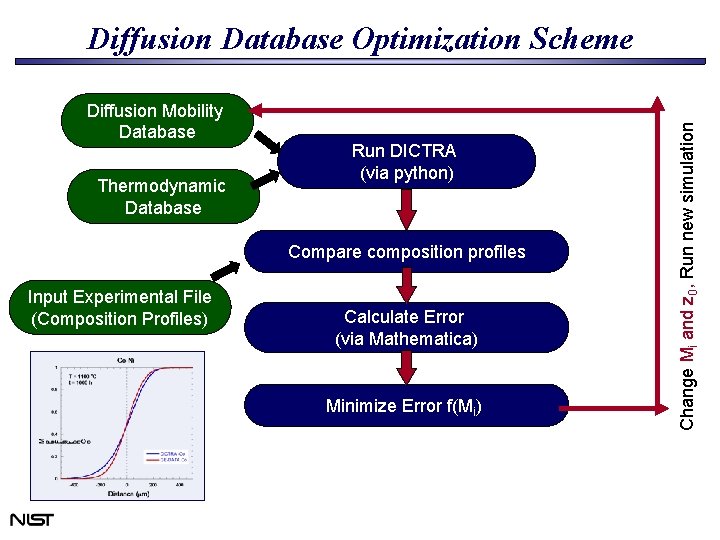
Diffusion Mobility Database Thermodynamic Database Run DICTRA (via python) Compare composition profiles Input Experimental File (Composition Profiles) Calculate Error (via Mathematica) Minimize Error f(Mi) Change Mi and z 0, Run new simulation Diffusion Database Optimization Scheme

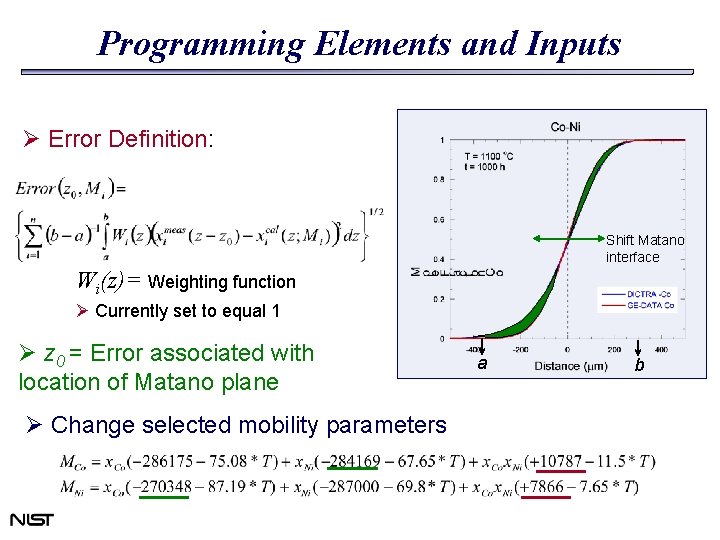
Programming Elements and Inputs Ø Error Definition: Shift Matano interface Wi(z)= Weighting function Ø Currently set to equal 1 Ø z 0 = Error associated with location of Matano plane Ø Change selected mobility parameters a b

Mobility Description Ni-W • FCC_A 1: Mobility of Ni – MQ(FCC_A 1, NI: VA; 0) = -28700+69. 8*T – MQ(FCC_A 1, W: VA; 0) = V 1+R*T*LN(V 2) – MQ(FCC_A 1, NI, W: VA; 0) = V 3+V 4*T • FCC_A 1: Mobility of W – MQ(FCC_A 1, NI: VA; 0) = V 5+R*T*LN(V 6) – MQ(FCC_A 1, W: VA; 0) = V 7+R*T*LN(V 8) – MQ(FCC_A 1, NI, W: VA; 0) = V 9+V 10*T

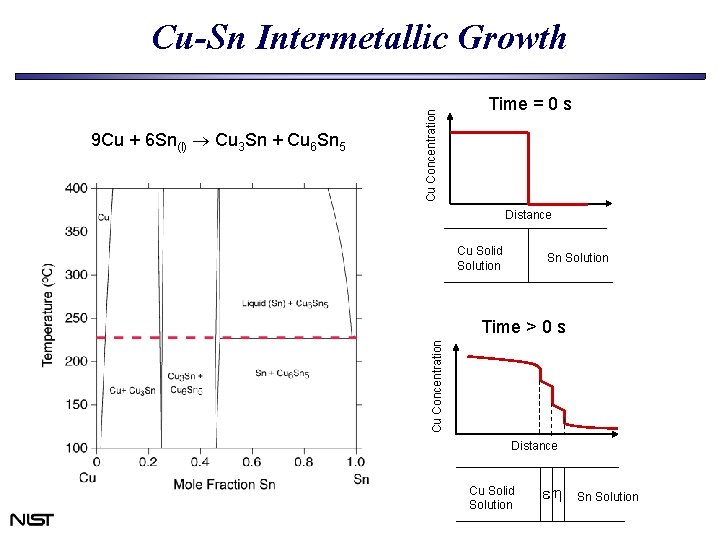
Time = 0 s Distance Cu Solid Solution Sn Solution Time > 0 s Cu Concentration 9 Cu + 6 Sn(l) Cu 3 Sn + Cu 6 Sn 5 Cu Concentration Cu-Sn Intermetallic Growth Distance Cu Solid Solution eh Sn Solution

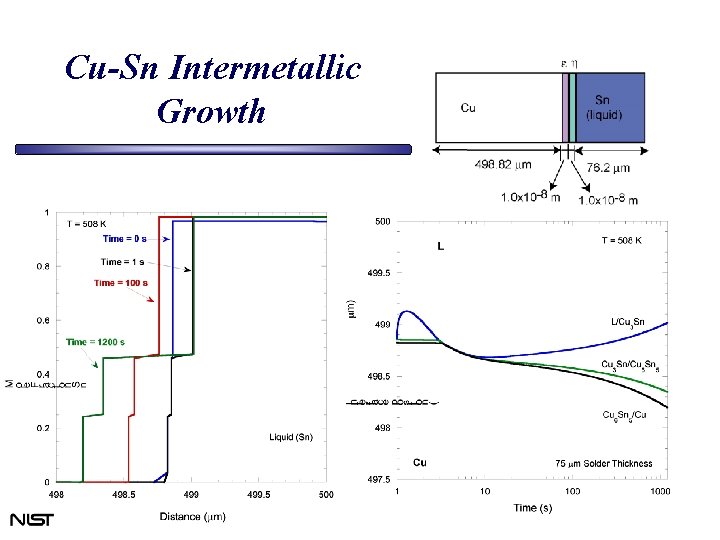
Cu-Sn Intermetallic Growth

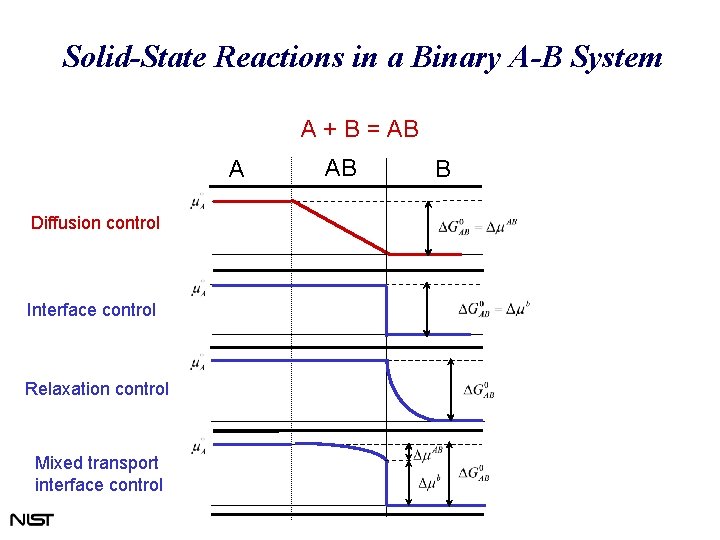
Solid-State Reactions in a Binary A-B System A + B = AB A Diffusion control Interface control Relaxation control Mixed transport interface control AB B

Definitions Coefficient General Notation Tracer Diffusivity Intrinsic Diffusivity (partial chemical) Chemical Diffusivity (Interdiffusion) (binary) are related by the velocity of Kirkendall frame, Mobility Notation