DEVELOPING THE CONCEPT OF EQUALITY IN MATHEMATICS GRADES






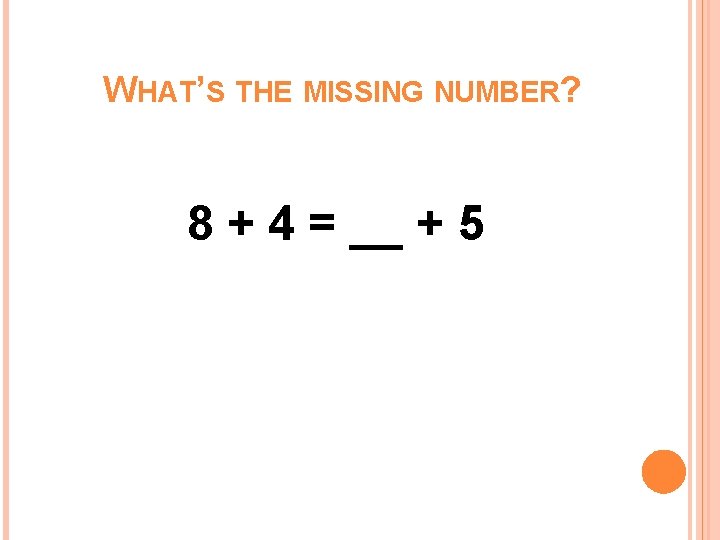
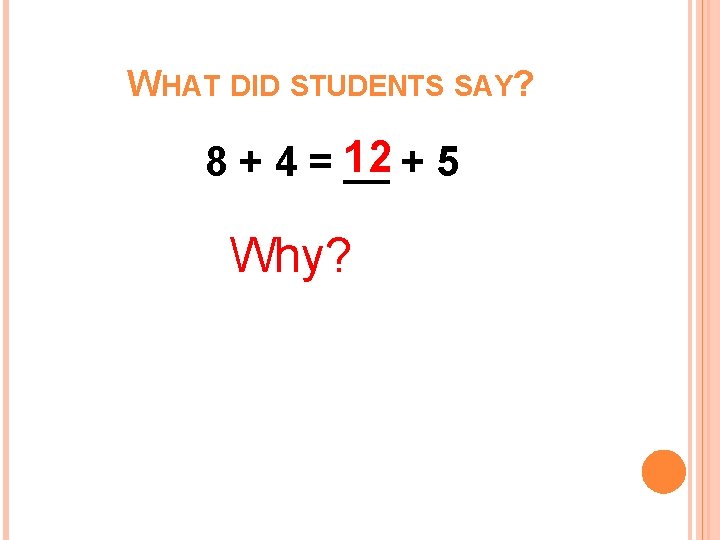
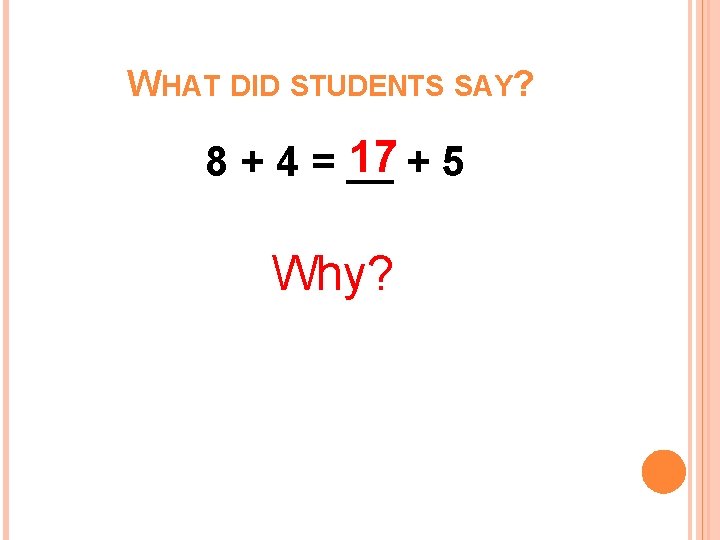
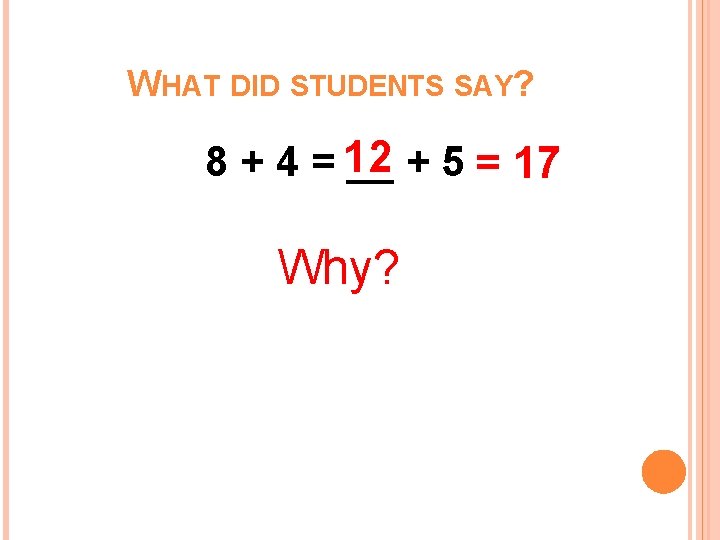
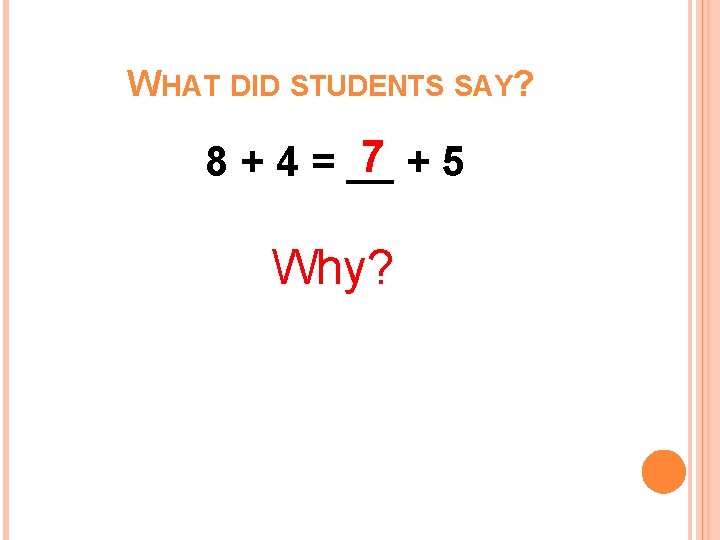
















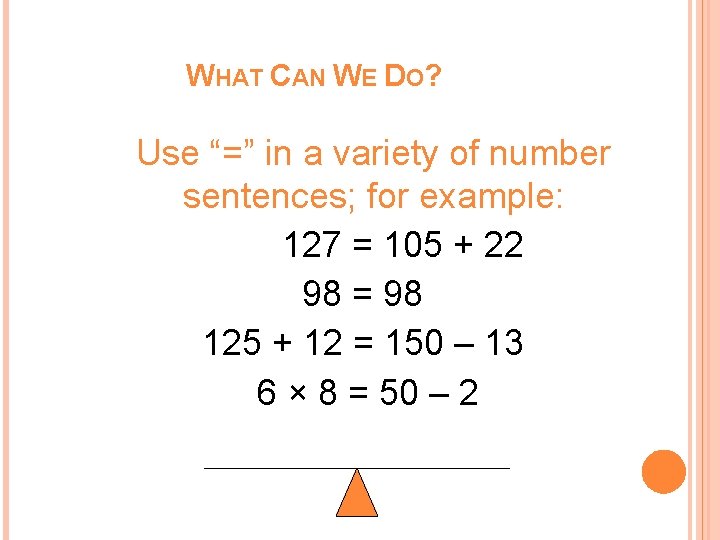













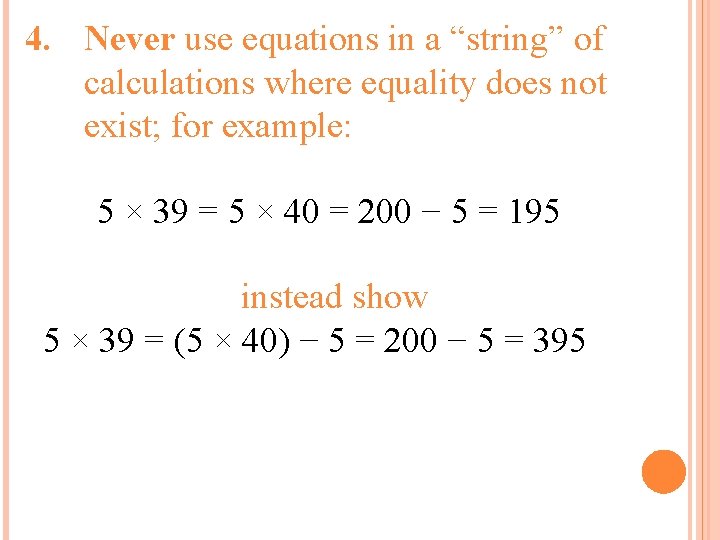






- Slides: 54

DEVELOPING THE CONCEPT OF EQUALITY IN MATHEMATICS: GRADES 4 -6 David Mc. Killop, Consultant Pearson Education

Before we begin… • If you have any questions during the presentation, please post them in the chat at the left of your screen, and we will spend some time during the webinar as a Q/A time. • This session will be recorded and the archive will be available within the next two weeks on the DVL website. http: //dvl. ednet. ns. ca • If you have technical difficulties, please call our help desk at (902) 424 -2450.

DESCRIPTION Equality is one of the essential understandings that students must acquire as they learn mathematics. This is a quest that begins in grade Primary and continues into senior high school. Learn how this big idea unfolds in Mathematics 4, 5, and 6 and discover how this one big idea can set students up for ongoing mathematical success.

DESCRIPTION Topics to be explored during this webinar will include creating and maintaining balance; the concept of a variable; expanding from the equal sign to greater than, less than, greater than or equal; and common misconceptions about equality.

GOALS OF WEBINAR To establish the need to re-consider how equality and the equal sign is taught To discuss some instructional strategies to help students develop a relational understanding of the equal sign To discuss some uses of the equal sign that should be avoided or never used To discuss why it is important that students have a relational understanding of the equal sign

IS THERE EVIDENCE TO SUPPORT OUR NEED TO ADDRESS EQUALITY?
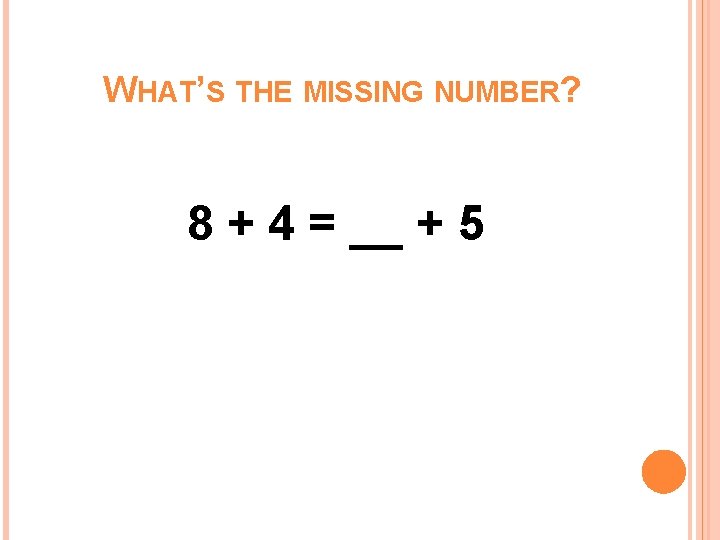
WHAT’S THE MISSING NUMBER? 8 + 4 = __ + 5
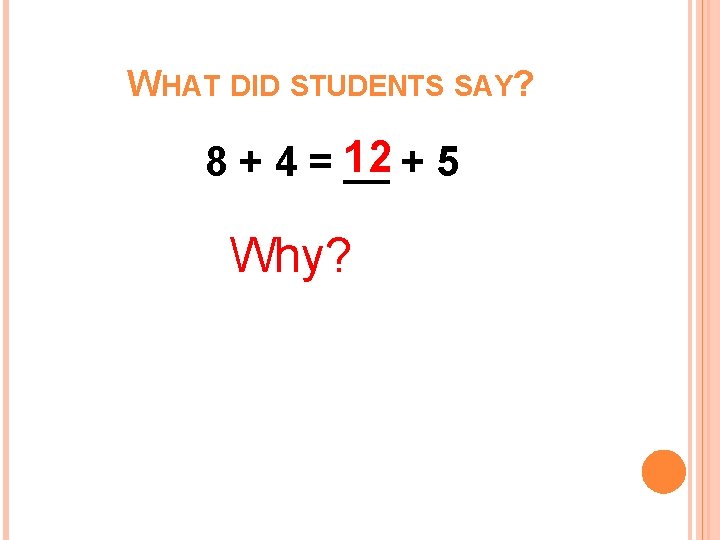
WHAT DID STUDENTS SAY? 8 + 4 = 12 __ + 5 Why?
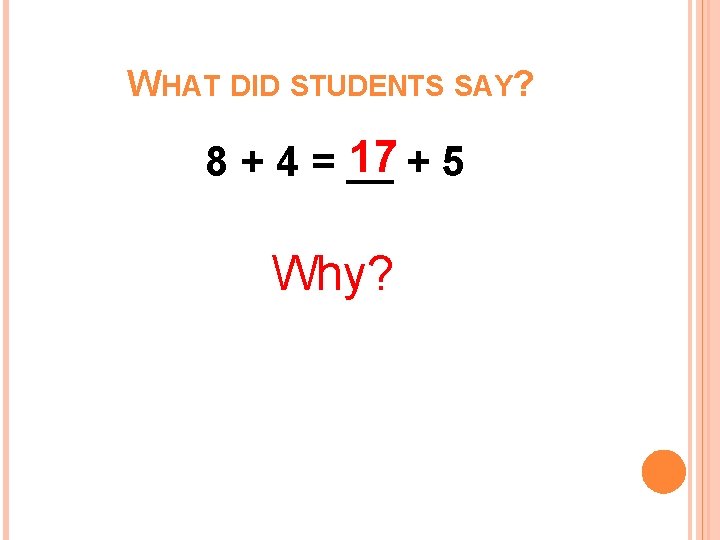
WHAT DID STUDENTS SAY? 17 + 5 8 + 4 = __ Why?
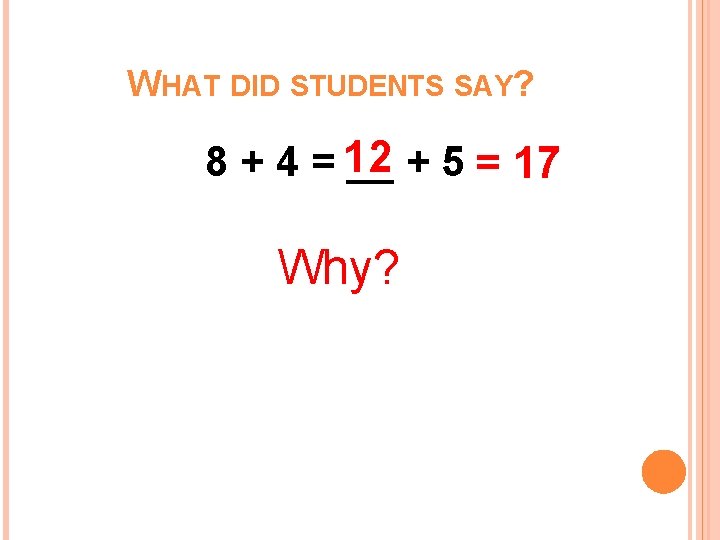
WHAT DID STUDENTS SAY? 8 + 4 = 12 __ + 5 = 17 Why?
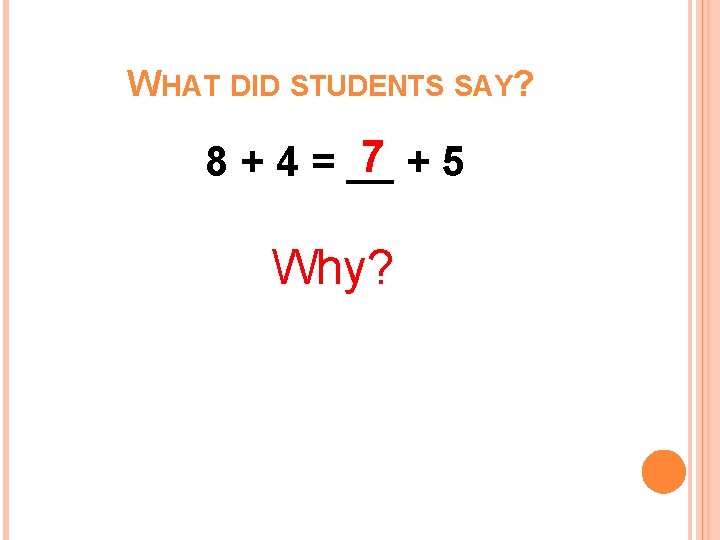
WHAT DID STUDENTS SAY? 7 +5 8 + 4 = __ Why?

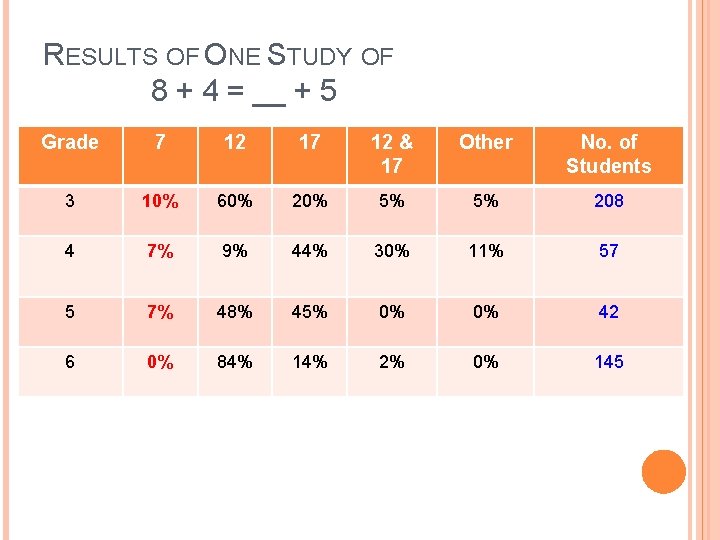
RESULTS OF ONE STUDY OF 8 + 4 = __ + 5 Grade 7 12 17 12 & 17 Other No. of Students 3 10% 60% 20% 5% 5% 208 4 7% 9% 44% 30% 11% 57 5 7% 48% 45% 0% 0% 42 6 0% 84% 14% 2% 0% 145

WHAT DOES THE “=” MEAN IN 4 + 3 ? =7 SOME STUDENT RESPONSES: “it means equal to” “it means 4 plus 3 equals 7” “what the sum of the two numbers are” “a sign connecting the answer to the problem” “how much the numbers added together equal” OPERATIONAL UNDERSTANDING

WHAT DOES THE “=” MEAN IN 4 + 3 ? =7 SOME STUDENTS RESPONSES “it means that what is to the left and right of the sign mean the same thing” “the same as, the same value” “the left side of the equals sign and the right side of the equals sign are the same value” RELATIONAL UNDERSTANDING

WITH AN OPERATIONAL VIEW, STUDENTS ALSO RESIST ACCEPTANCE OF… 8=5+3 “The sentence is wrong. It’s backward. ” 7=7 “This isn’t right. There’s no operation. ”

A MISUNDERSTANDING Teachers and researchers have long recognized that students tend to misunderstand the equal sign as an operator, that is, a signal for “doing something” rather than a relational symbol of equivalence or quantity sameness.

WHY AN OPERATIONAL VIEW? RESEARCHERS SUGGEST POSSIBLE FACTORS: ü ü ü False generalization because of the frequency of number sentences with operations on the left of the equal sign and answers on the right, in both texts and in lessons Use of calculators may reinforce this false generalization Children may have a predisposition to think of equality as calculating answers

WHAT WOULD YOUR STUDENTS FILL IN THE BLANK FOR 8 + 4 = ___ + 5? Because this is a diagnostic assessment, students should not be asked this question immediately after the concept of equality has been taught or discussed. They should be asked the question “out of the blue” to find out what they would respond spontaneously.
QUESTIONS

GIVEN WE HAVE A PROBLEM, WHAT CAN WE DO TO HELP MORE STUDENTS REACH RELATIONAL UNDERSTANDING?

WHAT CAN WE DO? Researchers concluded cognitive development (Collis, 1974) as well as instruction to be contributing factors to viewing the equal sign as relational. The pervading view is that teachers at all grade levels need to include instruction directly aimed at helping students develop a relational understanding of equality.

WHAT CAN WE DO? Help students connect their intuitive sense of “balance” from teetertotter and pan balance experiences to equality of two sides of number sentences.

SIMULATING A BALANCED TEETER-TOTTER

PAN BALANCES

PAN BALANCE AND BASE-TEN BLOCKS: ACTIVITY 1 Using a uniform set of base-ten blocks, place 6 rods and 4 small cubes in zip-lock bag A, and 2 rods and 3 small cubes in another zip-lock-bag B. Place bags A and B on the left pan, and 2 empty zip-lock bags on the right pan. Now start placing rods on the right pan, counting them as you do. When 9 rods are reached and it is obviously too much, remove a rod and start counting small cubes until it is balanced. Write this situation as a number sentence: 64 + 23 = 87. Reverse contents of the pans. Write this balance as 87 = 64 + 23. Repeat with other combinations of blocks, including flats; however, use numbers that will require NO trading unless you know that 10 small cubes in your set has the same mass as a rod and/or 10 rods has the same mass as a flat. )

PAN BALANCE AND BASE-TEN BLOCKS: ACTIVITY 2 Using a uniform set of base-ten blocks, place 3 rods and 2 small cubes in zip-lock bag A, 4 rods and 3 small cubes in zip-lock-bag B, and 5 rods and 1 small cubes in zip-lock bag C. Place bags A and B on the left pan, and bag C and 1 empty ziplock bag on the right pan. Now start placing rods on the right pan, counting them as you do. When 3 rods are reached and it is obviously too much, remove a rod and start counting small cubes until it is balanced. Write this situation as a number sentence: 32 + 43 = 51 + 24 Reverse contents of the pans. Write this balance as 51 + 24 = 32 + 43 Repeat with other combinations of blocks, including flats; however, use numbers that will require NO trading unless you know that 10 small cubes in your set has the same mass as a rod and/or 10 rods has the same mass as a flat.

PAN BALANCE AND BASE-TEN BLOCKS: ACTIVITY 3 Using a uniform set of base-ten blocks, place a set of 7 rods and 5 small cubes in each of two zip-lock bags. Place one bag on each pan of the balance. Write this situation as a number sentence: 75 = 75

WHAT CAN WE DO? Explicitly teach and use several synonyms for “=” and encourage students to use: “is the same as”, “has the same value as”, “balances”, “is worth the same”, “is equivalent to”

WHAT CAN WE DO? Use a picture of a balance scale or teeter-totter as a visual reminder
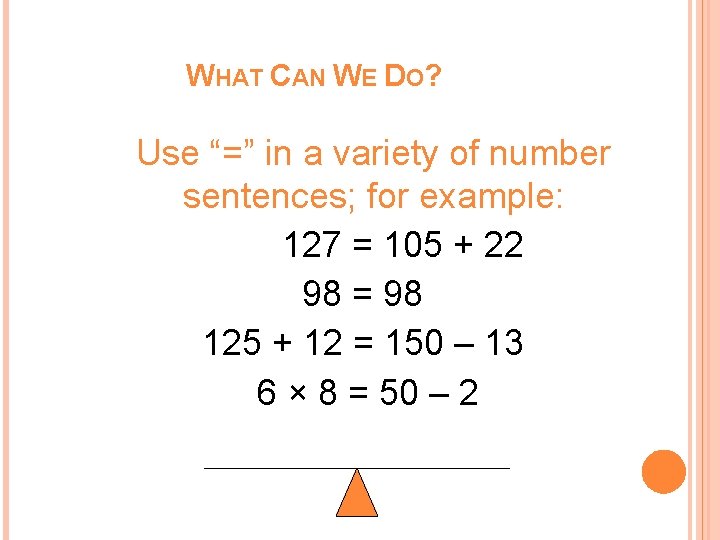
WHAT CAN WE DO? Use “=” in a variety of number sentences; for example: 127 = 105 + 22 98 = 98 125 + 12 = 150 – 13 6 × 8 = 50 – 2

WHAT CAN WE DO? Vary the position of the unknown in open number sentences; for example: 125 + = 180 380 = + 130 × 25 = 500 400 ÷ 8 = + 10

WITH SINGAPORE DIAGRAMS, WRITE ALL THE POSSIBLE OPEN NUMBER SENTENCES: 220 ? 565 220 + ? = 565 = 220 + ? 565 – 220 = ? 565 – ? = 220 = 565 – ? 1. 5 ? 2. 8 1. 5 + ? = 2. 8 = 1. 5 + ? 2. 8 – 1. 5 = ? 2. 8 – ? = 1. 5 = 2. 8 – ?

HAVE STUDENTS CONSIDER NUMBER STATEMENTS AS TRUE OR FALSE 123 + 154 = 154 + 123 154 + 21 = 154 + 23 26 – 26 = 71 – 71 150 – 76 = 150 – 74 51 + 51 = 50 + 52

HAVE STUDENTS CREATE TRUE-FALSE STATEMENTS a) __ + __ = __ + __ b) __ − __ = __ − __ c) __ + __ = __ − __

EXPANDING RELATIONAL UNDERSTANDING OF THE EQUAL SIGN With cognitive growth and experiences, students should move from using calculations to establish or verify equality to making decisions based on perceived relationships among the numbers in the expressions on each side of the equal sign. 264 + __ = 260 + 13 Is this true? 261 + 179 = 179 + 261 Is this true? 122 – 48 = 122 – 54

Fill in the blanks without actually doing any of the indicated calculations, and explain how you reasoned the solutions. a) b) c) d) e) f) 212 + 313 = ___ + 212 540 + 150 = 545 + ___ 760 – 142 = 768 – ___ 48 × 50 = 24 × ___ 25 × 36 = 100 × ___ 678 ÷ 4 = 678 × ___

Replace the boxes with =, >, or < to make true number sentences: a) b) c) d) e) f) g) 21 + 13 54 – 18 75 + 12 48 + 14 6× 9 36 ÷ 3 5. 6 + 2. 4 23 + 11 19 + 18 68 + 17 75 – 13 7× 8 24 ÷ 3 4× 2

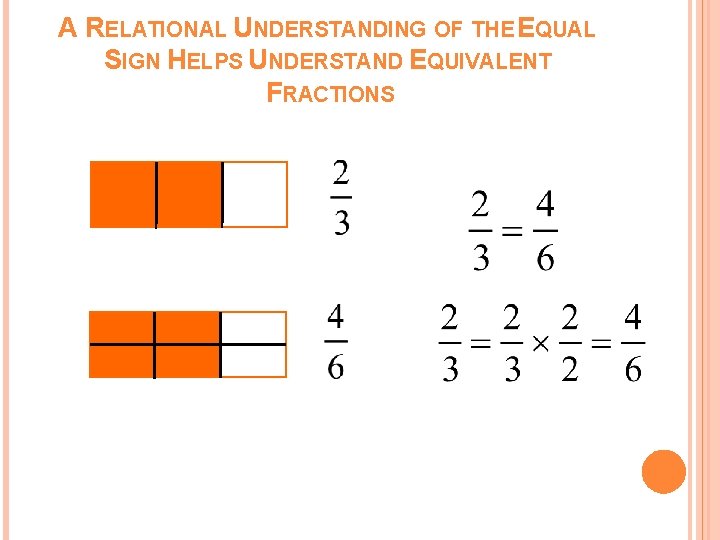
A RELATIONAL UNDERSTANDING OF THE EQUAL SIGN HELPS UNDERSTAND EQUIVALENT FRACTIONS

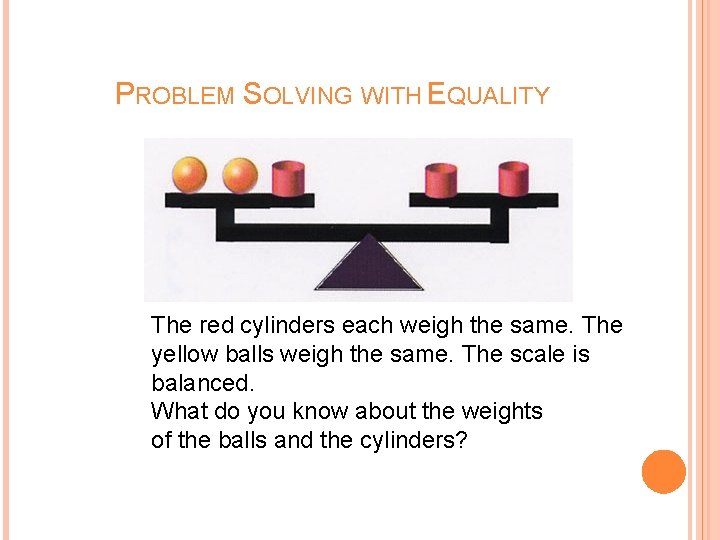
PROBLEM SOLVING WITH EQUALITY The red cylinders each weigh the same. The yellow balls weigh the same. The scale is balanced. What do you know about the weights of the balls and the cylinders?

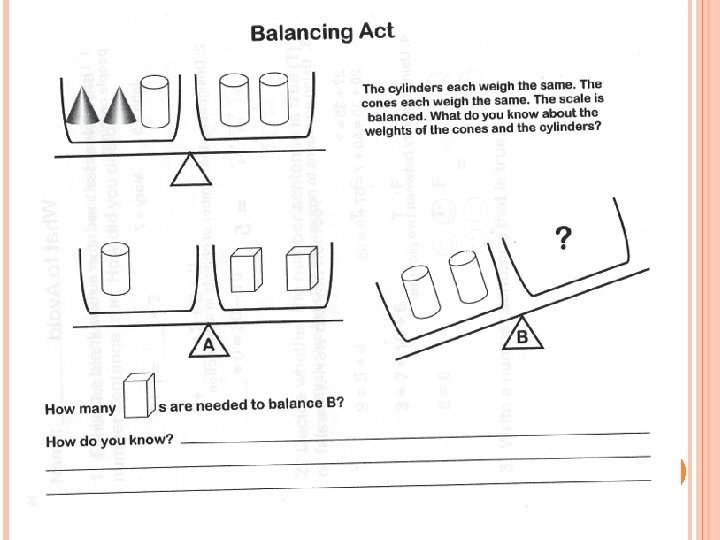
PROBLEM SOLVING WITH EQUALITY Each purple cylinder weighs the same. Each blue cylinder weighs the same. The scale is balanced. What do you know about the weights of the cylinders?

QUESTIONS

SOMETHING TO CONSIDER The equal sign (=) is a symbol. It should only be used with other symbols, as in symbol sentences. A picture may be used to “represent” a number, but the picture is not “the same as” that number.

SO, WHAT SHOULD WE AVOID? 1. Listing the ages or some other numerical characteristic of people or things: John = 8 Mary = 7

SO, WHAT SHOULD WE AVOID? 2. Designating the number of objects in a collection using “=”: = 5

SO, WHAT SHOULD WE AVOID? 3. Using an “=” between two pictures: =

4. Never use equations in a “string” of calculations where equality does not exist; for example: 27 + 38 = 20 + 30 = 50 + 7 = 57 + 8 = 65 instead show 27 + 38 = (20 + 30) + 7 + 8 = 57 + 8 = 65
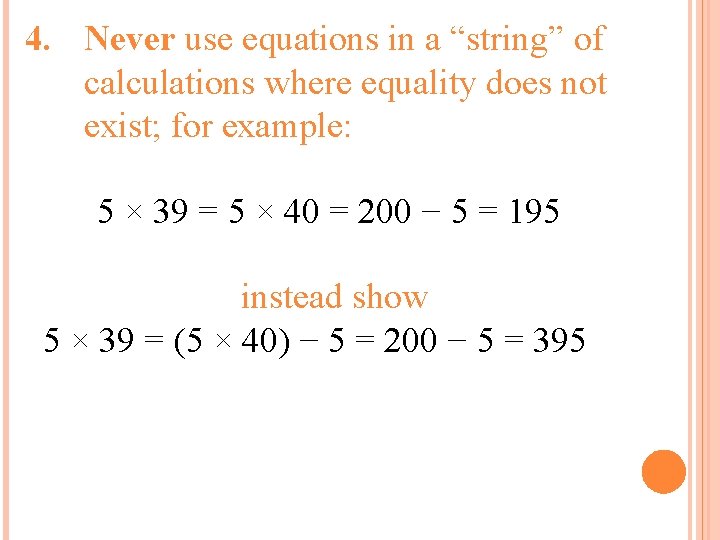
4. Never use equations in a “string” of calculations where equality does not exist; for example: 5 × 39 = 5 × 40 = 200 − 5 = 195 instead show 5 × 39 = (5 × 40) − 5 = 200 − 5 = 395

WHY IS IT IMPORTANT FOR STUDENTS TO HAVE A RELATIONAL UNDERSTANDING OF THE EQUAL SIGN?

It helps students develop number relationships that is essential for number sense development. Understanding and using algebra depends upon a relational view of the equal sign, among other concepts. a. Researchers have found that a lack of a sophisticated view of the equal sign is associated with poor performance on equation-solving items. b. Researchers propose that long-standing misconceptions about the equal sign may be the root cause of high school students’ difficulties dealing with polynomial expressions. In short, efforts to enhance students’ understanding of the equal sign may pay off in better performance in algebra.

A Little History of the Equal Sign The "=" symbol that is now universally accepted by mathematics for equality was first recorded by Welsh mathematician Robert Recorde in The Whetstone of Witte (1557). The original form of the symbol was much wider than the present form.

In his book Recorde explains his design of the "Gemowe lines" (meaning twin lines, from the Latin gemellus): “… to avoid the tedious repetition of these words: "is equal to", I will set (as I do often in work use) a pair of parallels, or Gemowe lines, of one length (thus =), because no two things can be more equal. ” The symbol '=' was not immediately popular. The symbol || was used by some and æ (or œ), from the Latin word aequalis meaning equal, was widely used into the 1700 s.

GOALS OF WEBINAR To establish the need to re-consider how equality and the equal sign is taught To discuss some instructional strategies to help students develop a relational understanding of the equal sign To discuss some uses of the equal sign that should be avoided or never used To discuss why it is important that students have a relational understanding of the equal sign

QUESTIONS AND CONTACT INFORMATION Eric Therrien ICT Consultant (Mathematics & Sciences) Eric. Therrien@novascotia. ca (902) 424 -5561 Robin Harris Mathematics Curriculum Services Robin. Harris@novascotia. ca (902) 424 -7387 This session has been recorded and the archive will be available within the next two weeks on the DVL website. http: //dvl. ednet. ns. ca/browse/results/taxonomy%3 A 169