Developing Computational Fluency Traditionally algorithms were taught as


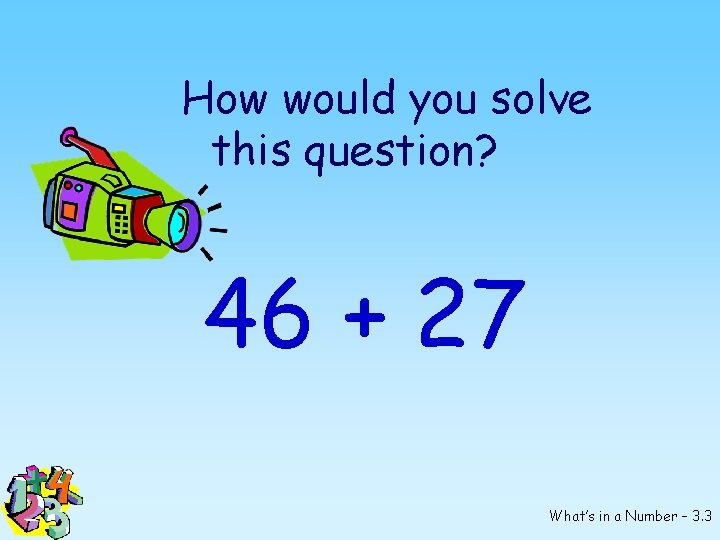










































- Slides: 54

Developing Computational Fluency Traditionally algorithms were taught as rote procedures to be memorized by students. Little consideration was given to UNDERSTANDING. Consequently students consistently made errors as they failed to ‘remember’ or confused algorithmic steps. What’s in a Number – 3. 1

Common Confusions Child says: “Add the numbers in each column and write the sums under the line” Child says: “You can’t subtract a number from zero, so you change the zeros into nines” 45 + 68 1013 99 500 - 257 342 What’s in a Number – 3. 2
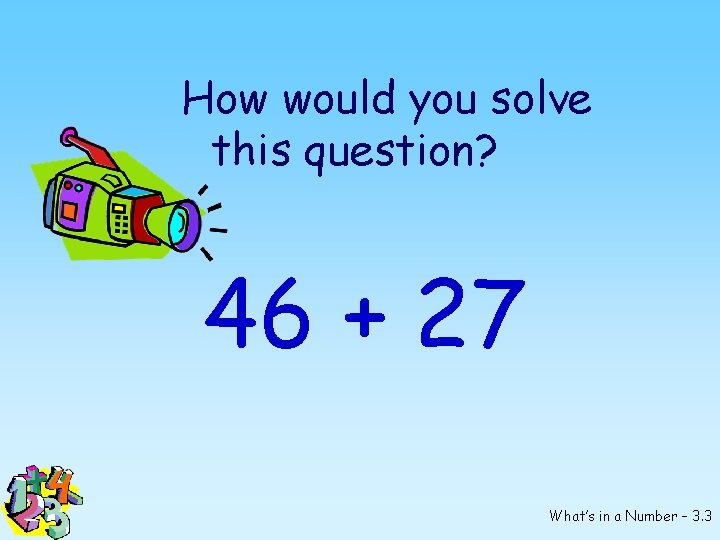
How would you solve this question? 46 + 27 What’s in a Number – 3. 3

Some possibilities: 40 plus 20 is 60 6 and 7 is 13 60 and 13 is 73 46 plus 20 is 66 66 plus 4 is 70 70 plus 3 is 73 1 46 +27 73 40 plus 20 is 60 6 plus 4 is 10 10 plus 60 is 70 The 3 left over is added to 70 to make 73 What’s in a Number – 3. 4

What Is A Basic Fact? Operations with single digit numbers (addition, subtraction, multiplication and division). 100 Addition Facts 100 Subtraction Facts 100 Multiplication Facts 90 Division Facts What’s in a Number – 3. 5

Three Steps To Fact Mastery • Help children develop a strong understanding of the operations and of number relationships. • Develop efficient strategies for fact retrieval. • Then provide practice in the use and selection of those strategies. John A. Van De Walle, What’s 2001, inp. 128 – 3. 6 a Number

Let’s Explore Some Basic Fact Strategies What’s in a Number – 3. 7

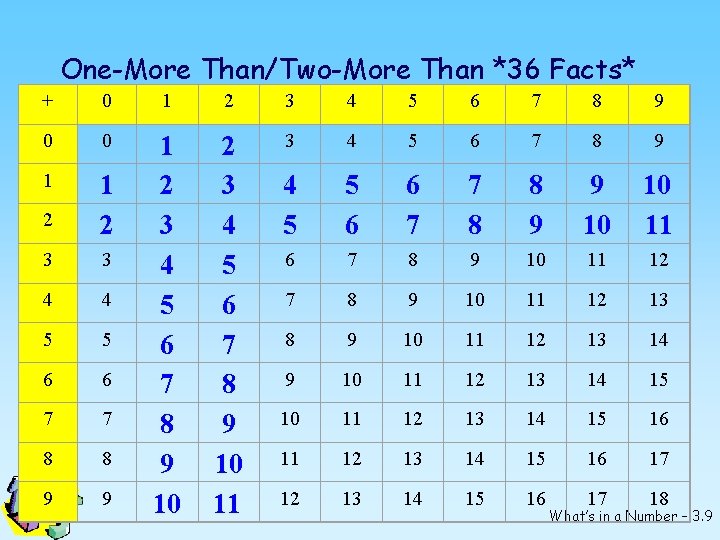
One More Than/Two More Than Facts This strategy covers 36 basic facts. They have either an addend of 1 or 2. 8 + 2 more 3 + 1 more What’s in a Number – 3. 8

One-More Than/Two-More Than *36 Facts* + 0 1 2 3 4 5 6 7 8 9 0 0 4 5 6 7 8 9 2 1 2 4 5 5 6 6 7 7 8 8 9 9 10 10 11 3 3 6 7 8 9 10 11 12 4 4 7 8 9 10 11 12 13 5 5 8 9 10 11 12 13 14 6 6 9 10 11 12 13 14 15 7 7 10 11 12 13 14 15 16 8 8 11 12 13 14 15 16 17 9 9 2 3 4 5 6 7 8 9 10 11 3 1 1 2 3 4 5 6 7 8 9 10 12 13 14 15 16 17 18 What’s in a Number – 3. 9

5 One More Than What’s in a Number – 3. 10

What’s in a Number – 3. 11

What’s in a Number – 3. 12

What’s in a Number – 3. 13

What’s in a Number – 3. 14

Two More Than Let’s try two more for the following dot plates. What’s in a Number – 3. 15

What’s in a Number – 3. 16

What’s in a Number – 3. 17

What’s in a Number – 3. 18

What’s in a Number – 3. 19

What’s in a Number – 3. 20

Zero Facts This strategy covers 19 basic facts. What’s in a Number – 3. 21

Facts With Zero *19 Facts* + 0 1 2 3 4 5 6 7 8 9 0 0 1 2 3 4 5 6 7 8 9 10 11 4 5 6 7 8 9 10 11 12 13 14 15 8 9 10 11 12 13 14 15 16 17 18 1 2 3 4 5 6 7 8 9 What’s in a Number – 3. 22

Zero Facts Zero Game What’s in a Number – 3. 23

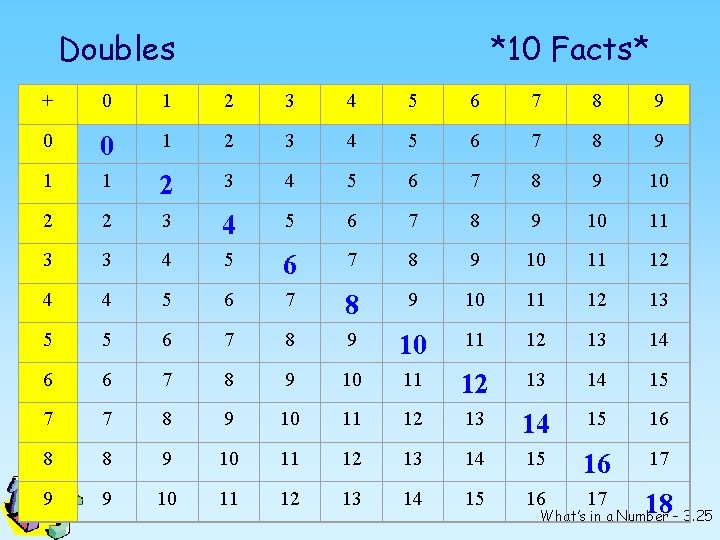
Doubles Facts There are only ten doubles facts from 0 + 0 to 9 + 9. One key thing for children to remember is that doubles are even answers and doubles plus one are odd answers What’s in a Number – 3. 24

Doubles *10 Facts* + 0 1 2 3 4 5 6 7 8 9 0 0 1 2 3 4 5 6 7 8 9 10 2 2 3 4 5 6 7 8 9 10 11 3 3 4 5 6 7 8 9 10 11 12 4 4 5 6 7 8 9 10 11 12 13 5 5 6 7 8 9 10 11 12 13 14 6 6 7 8 9 10 11 12 13 14 15 7 7 8 9 10 11 12 13 14 15 16 8 8 9 10 11 12 13 14 15 16 17 9 9 10 11 12 13 14 15 16 17 18 What’s in a Number – 3. 25

Doubles Flash Think about what the double is… Hold up your number card if the number is you! What’s in a Number – 3. 26

What’s in a Number – 3. 27

What’s in a Number – 3. 28

What’s in a Number – 3. 29

What’s in a Number – 3. 30

What’s in a Number – 3. 31

What’s in a Number – 3. 32

What’s in a Number – 3. 33

What’s in a Number – 3. 34

What’s in a Number – 3. 35

Doubles Nicknames 3+3=6 Insect Double (3 legs on each side) 4+4=8 Spider Double (4 legs on each side) 5 + 5 = 10 Fingers Double (5 fingers on each hand) 6 + 6 = 12 Farmer’s Double (12 eggs) 7 + 7 = 14 Valentine’s Double (February 14) 8 + 8 = 16 Sweet Sixteen or Sweetheart Double What’s in a Number – 3. 36

Anchors of Five and Ten What’s in a Number – 3. 37

Make Ten Facts Children need to know what number they can add to any number to make 10 or a multiple of 10. Using a ten frame is beneficial. What’s in a Number – 3. 38

Make Ten Flash What do we need to make 10? What do we need to answer the question? What’s in a Number – 3. 39

What is 8 + 7 ? What’s in a Number – 3. 40

What is 9 + 6 ? What’s in a Number – 3. 41

What is 7 + 6 ? What’s in a Number – 3. 42

What is 8 + 3 ? What’s in a Number – 3. 43

Subtraction as Think-Addition Using known addition facts to produce what the unknown quantity is in the sentence. “Julian had 6 marbles in his bag. George gave him more marbles. Then he had 14 marbles. How many marbles did George give Julian? ” What’s in a Number – 3. 44

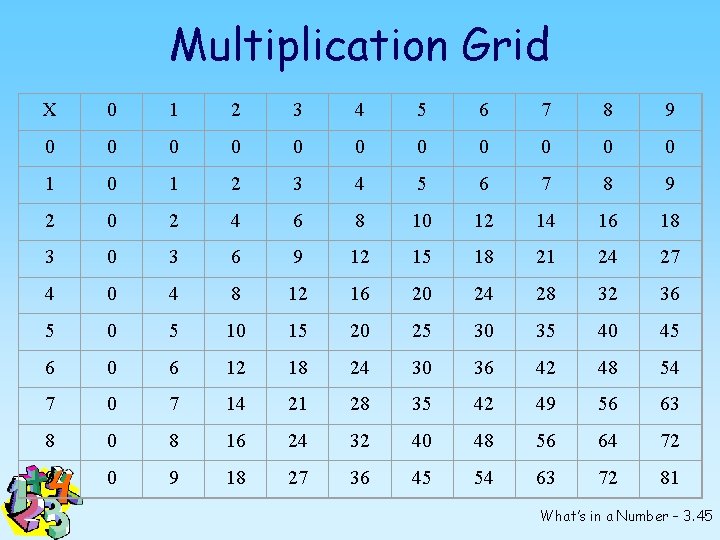
Multiplication Grid X 0 1 2 3 4 5 6 7 8 9 0 0 0 1 2 3 4 5 6 7 8 9 2 0 2 4 6 8 10 12 14 16 18 3 0 3 6 9 12 15 18 21 24 27 4 0 4 8 12 16 20 24 28 32 36 5 0 5 10 15 20 25 30 35 40 45 6 0 6 12 18 24 30 36 42 48 54 7 0 7 14 21 28 35 42 49 56 63 8 0 8 16 24 32 40 48 56 64 72 9 0 9 18 27 36 45 54 63 72 81 What’s in a Number – 3. 45

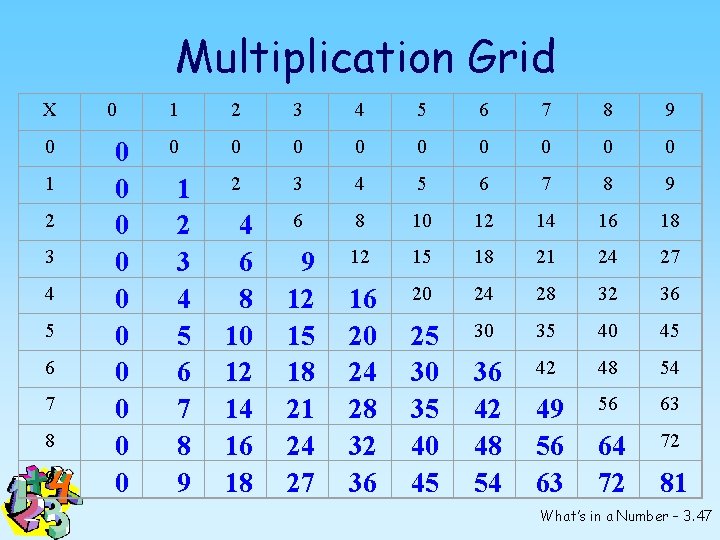
Commutative Property The Flip-Flop Strategy! The order of the two numbers does not affect their sum for addition or their product for multiplication. 3 + 5 = 8 or 5 + 3 = 8 3 x 5 = 15 or 5 x 3 = 15 What’s in a Number – 3. 46

Multiplication Grid X 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 2 3 4 5 6 7 8 9 4 6 8 10 12 14 16 18 9 12 15 18 21 24 27 16 20 24 28 32 36 25 30 35 40 45 36 42 48 54 49 56 63 64 72 72 1 2 3 4 5 6 7 8 9 81 What’s in a Number – 3. 47

One More Than/Two More Than Facts Zero Facts Doubles Facts 5 -3=2 2+3=5 Make Ten Facts Subtraction as Think. Addition Commutative Property What’s in a Number – 3. 48


lp He “Teachers who use timed tests believe that the tests help children learn basic facts. This perspective makes no instructional sense. Children who perform well under time pressure display their skills. Children who have difficulty with skills or who work more slowly run the risk of reinforcing wrong practices under pressure. Also, they can become fearful about, and negative toward, their mathematics learning. ” (Marilyn Burns, 1995, p. 408) What’s in a Number – 3. 50


Using Doubles 2 + 3 = ___ 3 + 4 = ___ 9 + 8 = ___ 8 + 7 = ___ 7 + 8 = ___ 7 + 6 = ___ 6 + 7 = ___ 6 + 5 = ___ 4 + 3 = ___ How do Doubles help you solve these questions? What’s in a Number – 3. 52 Strategy: _________

Timed Test !Children who are good at it get positive reinforcement. !It discourages the use of double-checking for accuracy. !It intimidates children who cannot recall the facts quickly but who may actually be very accurate. !It creates negative attitudes about mathematics in children who are not competitive. !It doesn’t provide a lens into the child’s thinking. It doesn’t tell the teacher what strategies the child is using. What’s in a Number – 3. 53

Basic Facts Assessment Even Number Is great Show all the ways you can use your basic facts strategies to make 8. Goes around twice Half of sixteen Two times four + What’s in a Number – 3. 54