Deterministic Finite State Machines Chapter 5 Languages and

Deterministic Finite State Machines Chapter 5

Languages and Machines 2

Regular Languages L Regular Expression Regular Language Accepts Finite State Machine 3

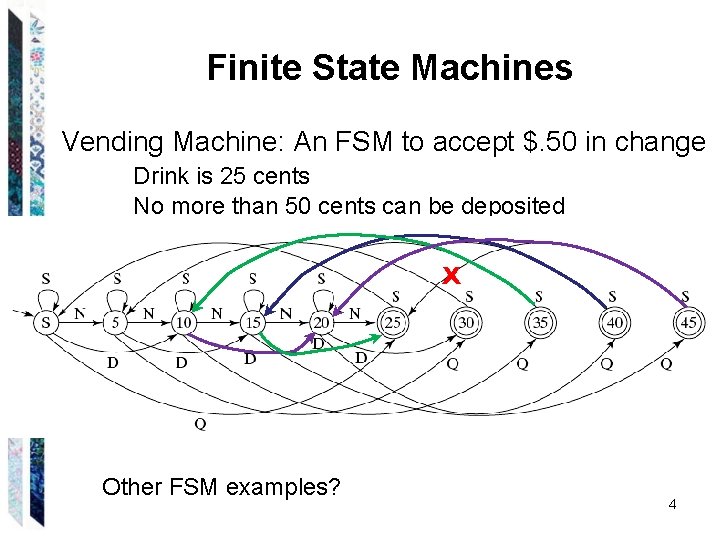
Finite State Machines Vending Machine: An FSM to accept $. 50 in change Drink is 25 cents No more than 50 cents can be deposited X Other FSM examples? 4

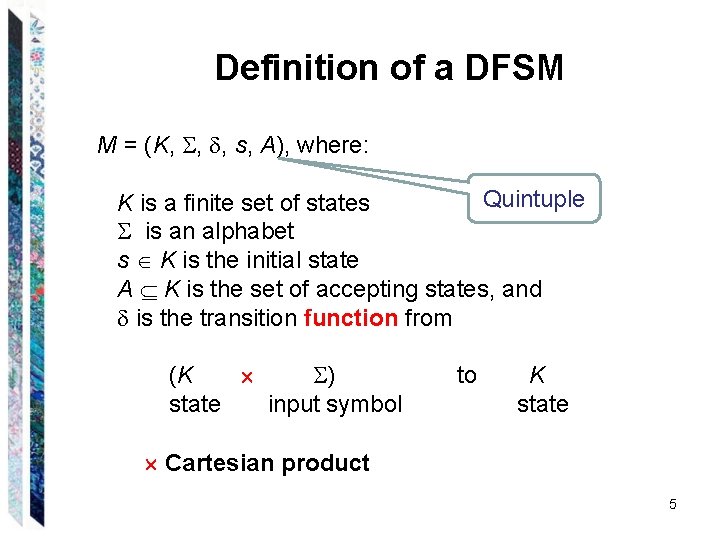
Definition of a DFSM M = (K, , , s, A), where: Quintuple K is a finite set of states is an alphabet s K is the initial state A K is the set of accepting states, and is the transition function from (K ) state input symbol to K state Cartesian product 5

Accepting by a DFSM Informally, M accepts a string w iff M winds up in some element of A when it has finished reading w. The language accepted by M, denoted L(M), is the set of all strings accepted by M. 6

Configurations of DFSMs A configuration of a DFSM M is an element of: K * It captures the two things that can make a difference to M’s future behavior: • its current state • the input that is still left to read. The initial configuration of a DFSM M, on input w, is: (s. M, w), where s. M is the start state of M 7

The Yields Relations The yields-in-one-step relation |-M : (q, w) |-M (q', w') iff • w = a w' for some symbol a , and • (q, a) = q' The relation yields, |-M*, is the reflexive, transitive closure of |-M. C 1 |-M* C 2 : M can go from C 1 to C 2 in 0 or more steps. 8

Computations Using FSMs A computation by M is a finite sequence of configurations C 0, C 1, …, Cn for some n 0 such that: • C 0 is an initial configuration, • Cn is of the form (q, ), for some state q KM, • C 0 |-M C 1 |-M C 2 |-M … |-M Cn. 9

Accepting and Rejecting A DFSM M accepts a string w iff: (s, w) |-M * (q, ), for some q A. A DFSM M rejects a string w iff: (s, w) |-M* (q, ), for some q AM. The language accepted by M, denoted L(M), is the set of all strings accepted by M. Theorem: Every DFSM M, on input s, halts in |s| steps. 10

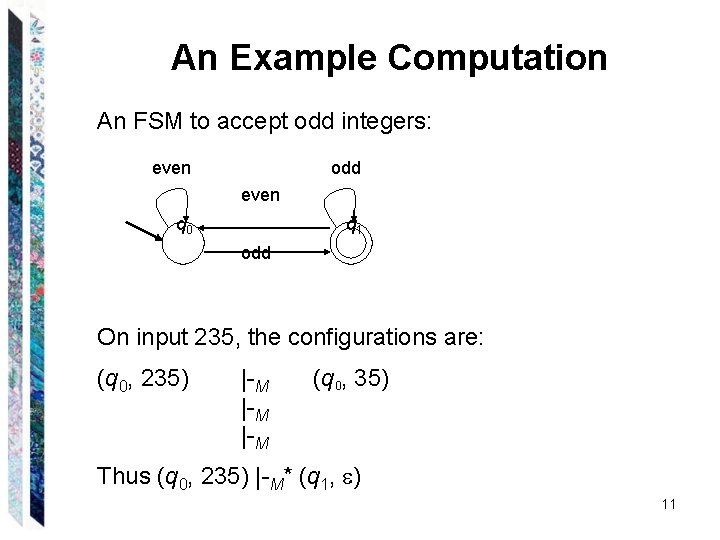
An Example Computation An FSM to accept odd integers: even odd even q 0 q 1 odd On input 235, the configurations are: (q 0, 235) |-M |-M (q 0, 35) Thus (q 0, 235) |-M* (q 1, ) 11

Regular Languages A language is regular iff it is accepted by some FSM. 12

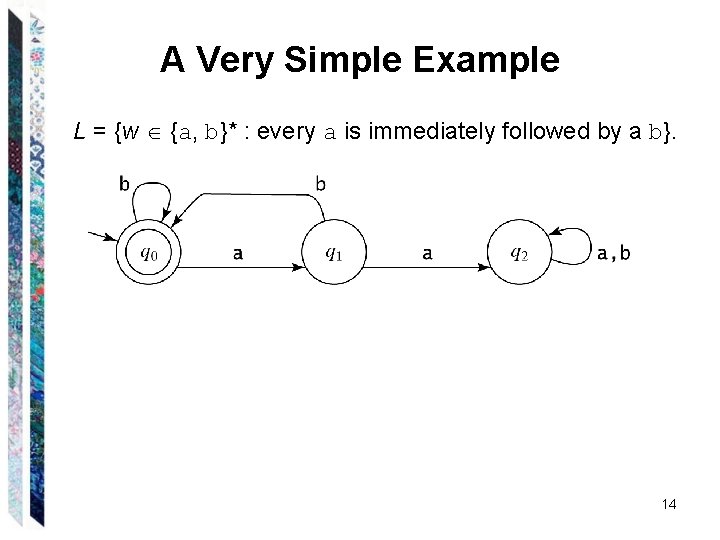
A Very Simple Example L = {w {a, b}* : every a is immediately followed by a b}. 13

A Very Simple Example L = {w {a, b}* : every a is immediately followed by a b}. 14

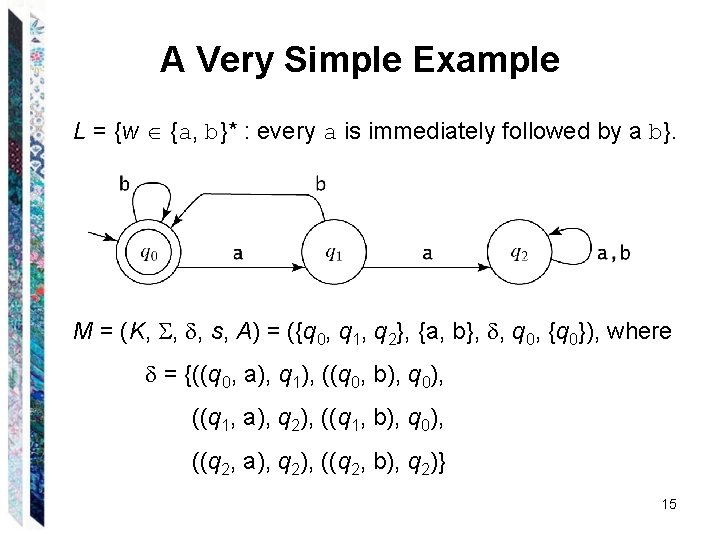
A Very Simple Example L = {w {a, b}* : every a is immediately followed by a b}. M = (K, , , s, A) = ({q 0, q 1, q 2}, {a, b}, , q 0, {q 0}), where = {((q 0, a), q 1), ((q 0, b), q 0), ((q 1, a), q 2), ((q 1, b), q 0), ((q 2, a), q 2), ((q 2, b), q 2)} 15

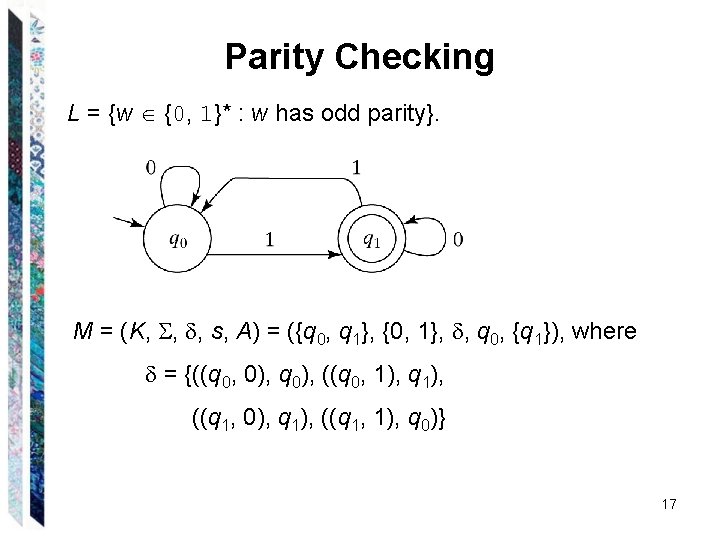
Parity Checking L = {w {0, 1}* : w has odd parity}. 16

Parity Checking L = {w {0, 1}* : w has odd parity}. M = (K, , , s, A) = ({q 0, q 1}, {0, 1}, , q 0, {q 1}), where = {((q 0, 0), q 0), ((q 0, 1), q 1), ((q 1, 0), q 1), ((q 1, 1), q 0)} 17

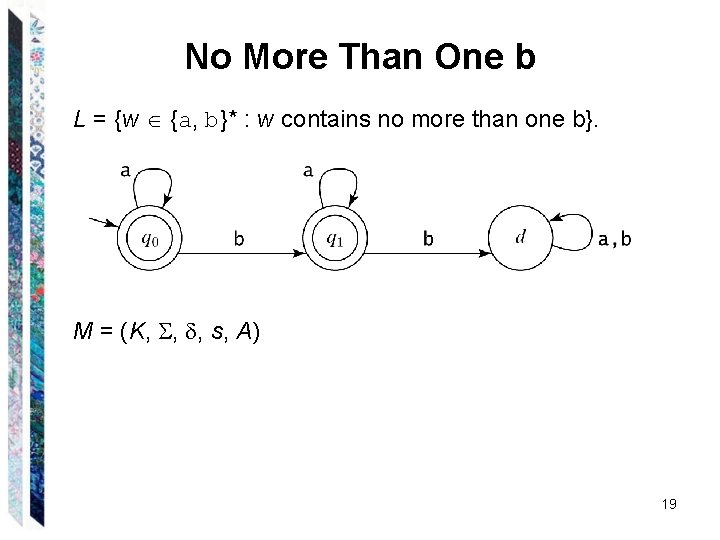
No More Than One b L = {w {a, b}* : w contains no more than one b}. 18

No More Than One b L = {w {a, b}* : w contains no more than one b}. M = (K, , , s, A) 19

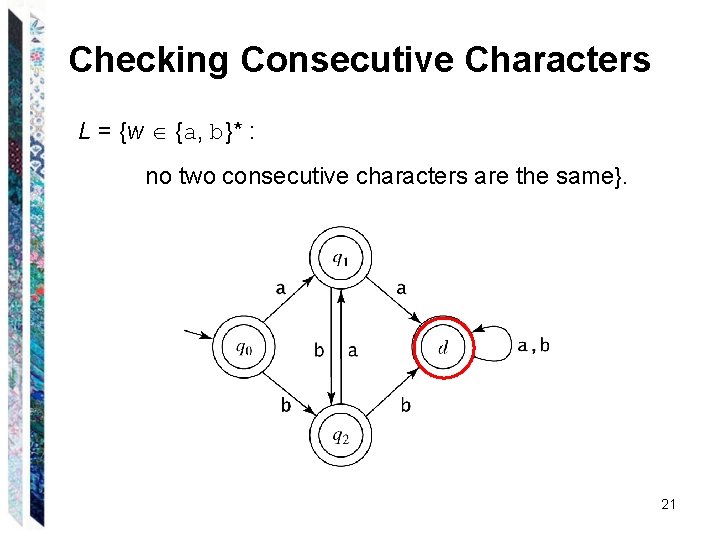
Checking Consecutive Characters L = {w {a, b}* : no two consecutive characters are the same}. 20

Checking Consecutive Characters L = {w {a, b}* : no two consecutive characters are the same}. 21

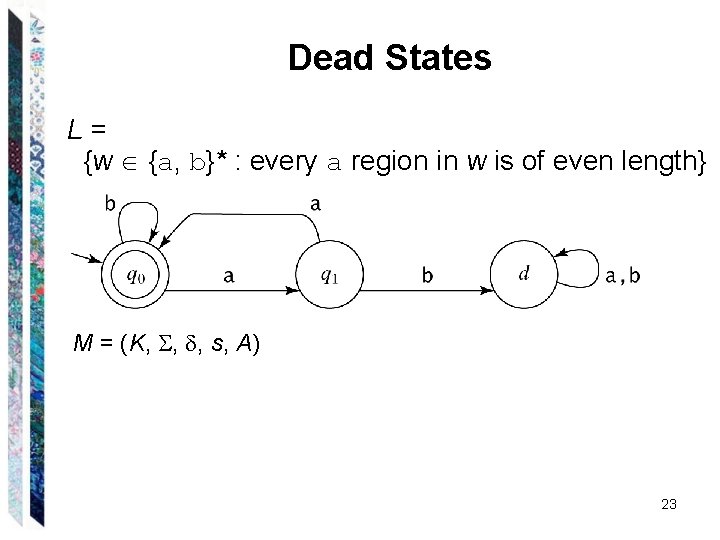
Dead States L= {w {a, b}* : every a region in w is of even length} 22

Dead States L= {w {a, b}* : every a region in w is of even length} M = (K, , , s, A) 23

Dead States L= {w {a, b}* : every b in w is surrounded by a’s} 24

The Language of Floating Point Numbers is Regular Example strings: +3. 0, 0. 3 E 1, 0. 3 E+1, -3 E 8 The language is accepted by the DFSM: 25

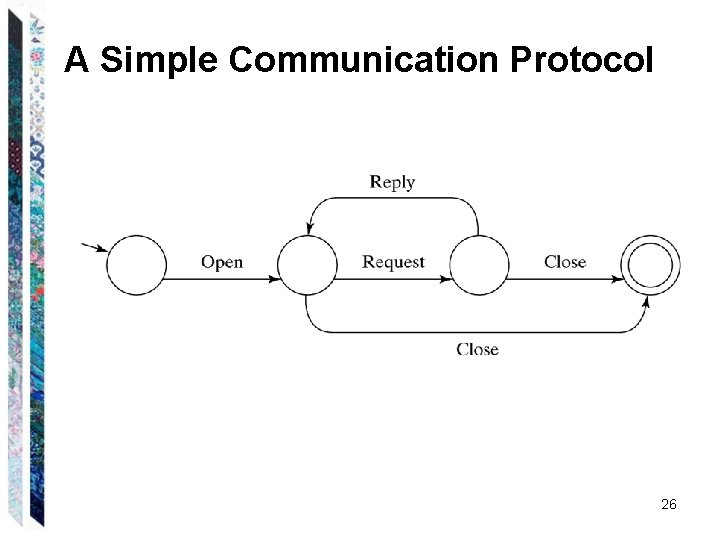
A Simple Communication Protocol 26

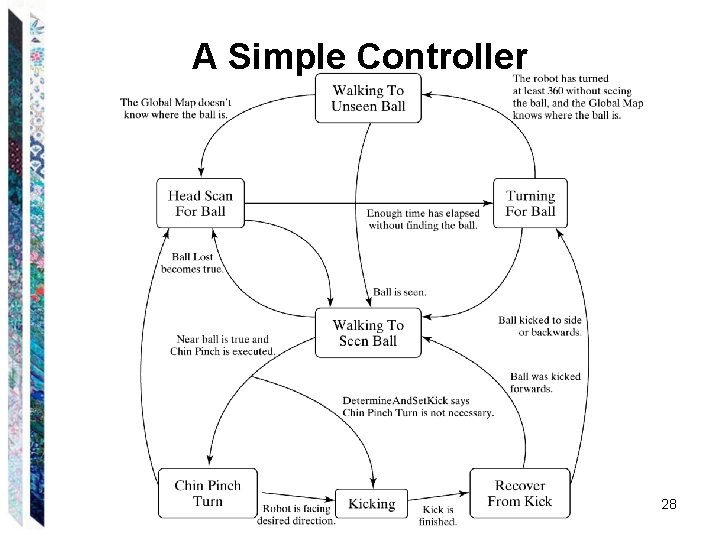
Controlling a Soccer-Playing Robot 27

A Simple Controller 28

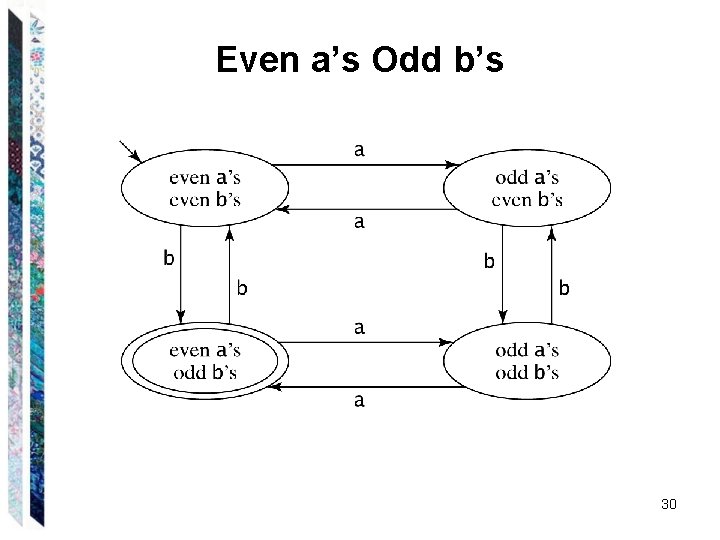
Programming FSMs Cluster strings that share a “future”. Let L = {w {a, b}* : w contains an even number of a’s and an odd number of b’s} What states are needed? How many states are there? 29

Even a’s Odd b’s 30

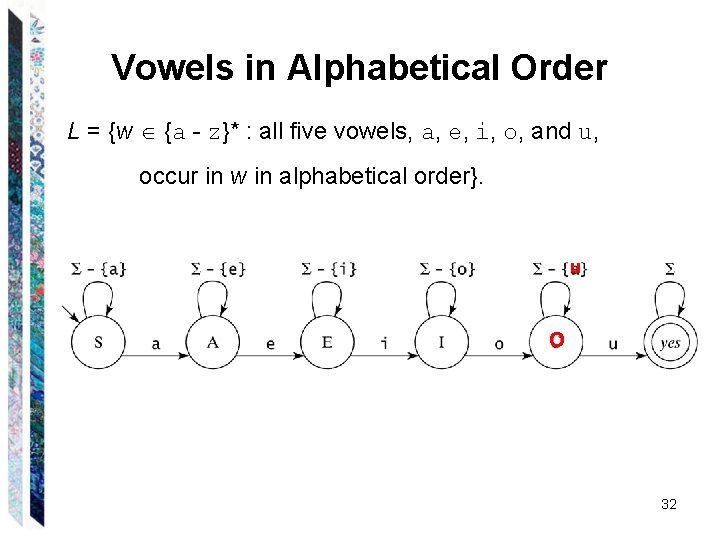
Vowels in Alphabetical Order L = {w {a - z}* : all five vowels, a, e, i, o, and u, occur in w in alphabetical order}. 31

Vowels in Alphabetical Order L = {w {a - z}* : all five vowels, a, e, i, o, and u, occur in w in alphabetical order}. u O 32

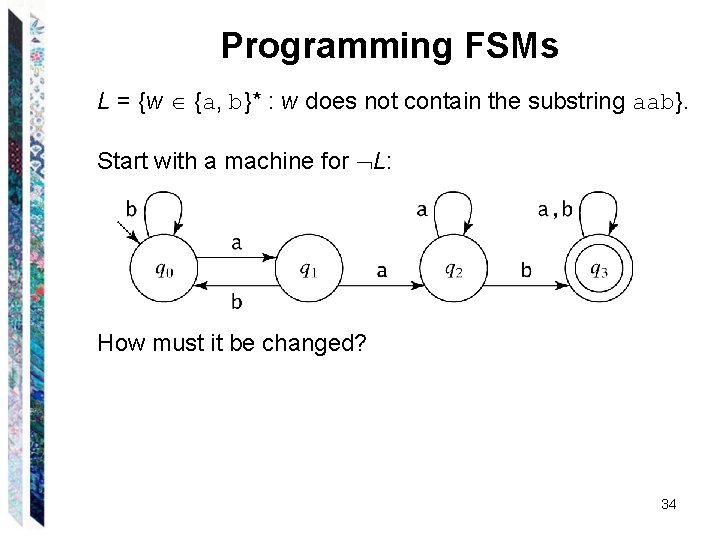
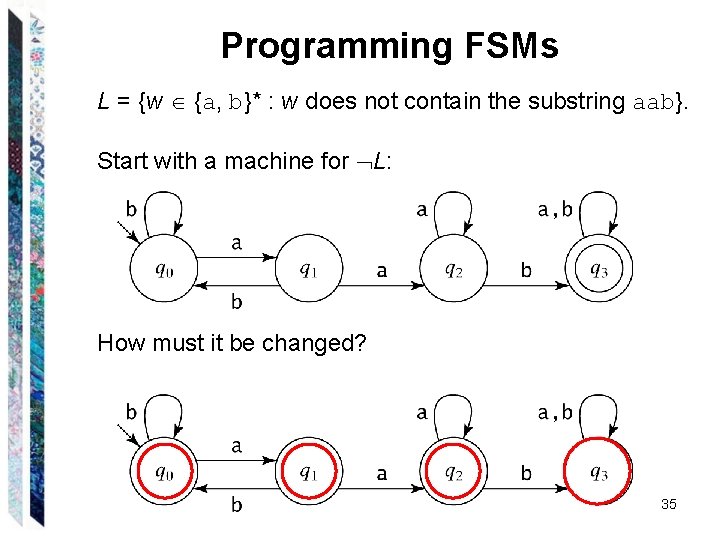
Programming FSMs L = {w {a, b}* : w does not contain the substring aab}. 33

Programming FSMs L = {w {a, b}* : w does not contain the substring aab}. Start with a machine for L: How must it be changed? 34

Programming FSMs L = {w {a, b}* : w does not contain the substring aab}. Start with a machine for L: How must it be changed? 35

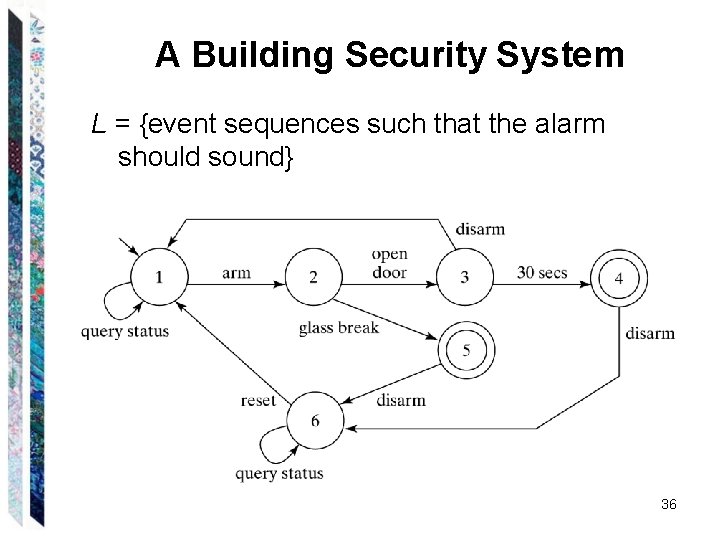
A Building Security System L = {event sequences such that the alarm should sound} 36

FSMs Predate Computers The Chinese Abacus, 14 century AD The Jacquard Loom, invented in 1801 The Prague Orloj, originally built in 1410 37

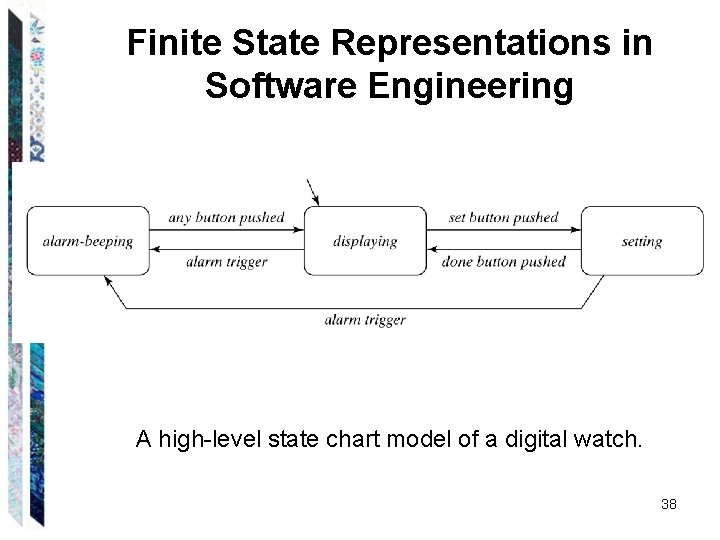
Finite State Representations in Software Engineering A high-level state chart model of a digital watch. 38

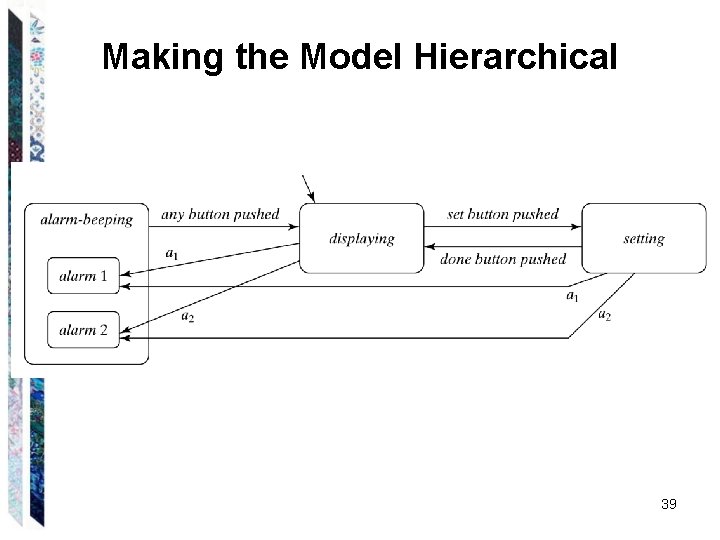
Making the Model Hierarchical 39

The Missing Letter Language Let = {a, b, c, d}. Let LMissing = {w : there is a symbol ai not appearing in w}. Try to make a DFSM for LMissing: 40