Deterministic Extractors for Small Space Sources Jesse Kamp

Deterministic Extractors for Small Space Sources Jesse Kamp, Anup Rao, Salil Vadhan, David Zuckerman

Outline The problem and results n Our Techniques n Extractor for linear min-entropy rate q Extractor for polynomial min-entropy rate q n Open Problems

Randomness Extractors X Ext Uniform Want efficient function Ext : {0, 1}n ! {0, 1}m s. t. for any weak source of randomness X, Ext(X) ~ Uniform Defn: (Min-Entropy) X has min-entropy k if Pr[X=x] · 2 -k for all x

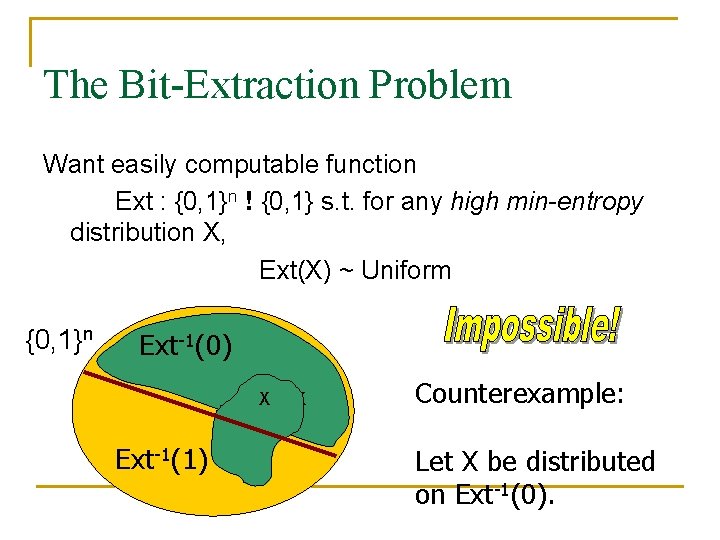
The Bit-Extraction Problem Want easily computable function Ext : {0, 1}n ! {0, 1} s. t. for any high min-entropy distribution X, Ext(X) ~ Uniform {0, 1}n Ext-1(0) X Ext-1(1) X Counterexample: Let X be distributed on Ext-1(0).

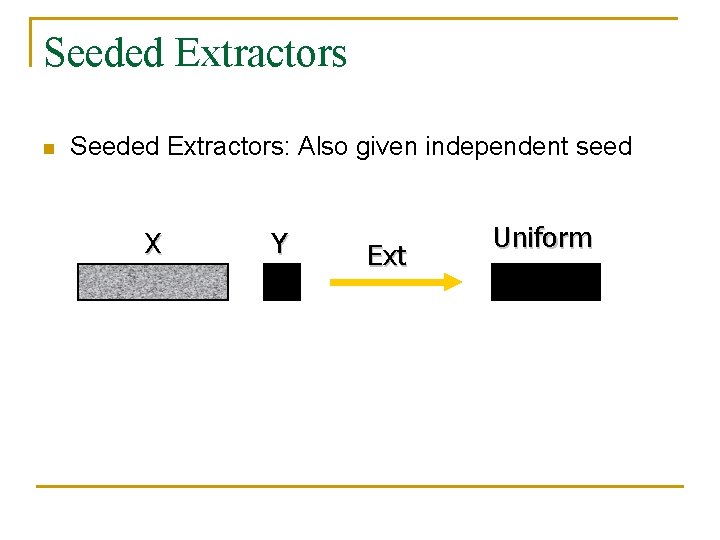
Seeded Extractors n Seeded Extractors: Also given independent seed X Y Ext Uniform

Independent Sources Ext Uniform

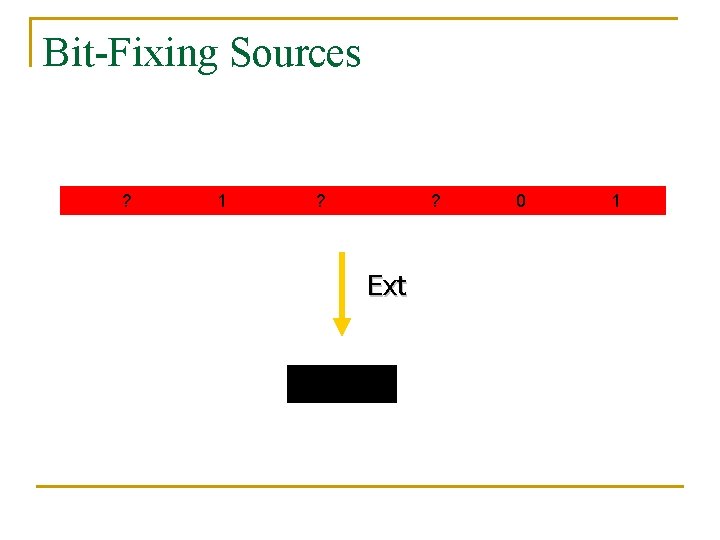
Bit-Fixing Sources ? 1 ? ? Ext 0 1

Applications n n n Derandomization Coding Theory Inapproximability Cryptography Extractors are Fundamental Combinatorial Objects. TM

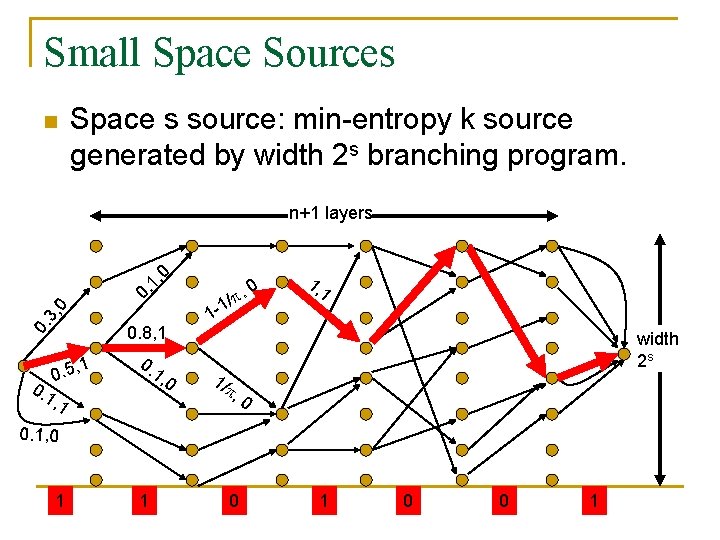
Small Space Sources n Space s source: min-entropy k source generated by width 2 s branching program. 0. 3, 0 0. 1, 0 n+1 layers 0. 1 1 0. 5, 0. 8, 1 0. 1, 0 , 1 0 / , 1 -1 1/ 1, 1 width 2 s , 0 0. 1, 0 1 1 0 0 1

Related Work n n n [Blum] gave explicit extractors for sources generated by Markov Chain with a constant number of states [Koenig, Maurer] considered a related model [Trevisan, Vadhan] considered sources sampled by small circuits (their extractors are based on complexity theoretic assumptions).

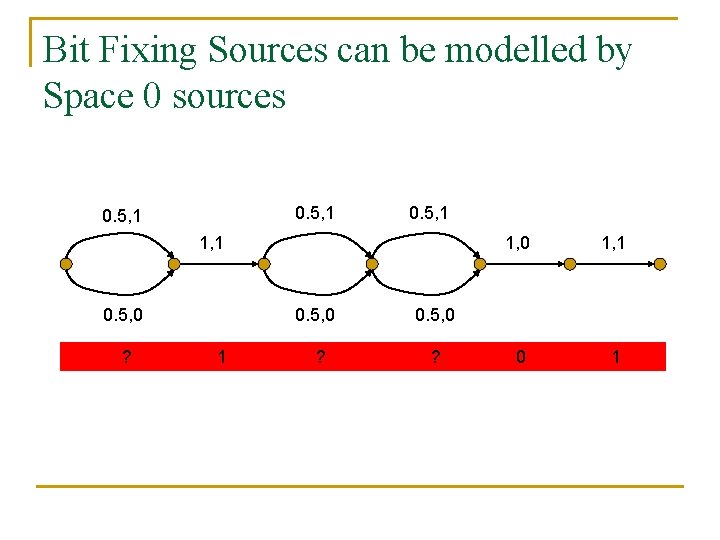
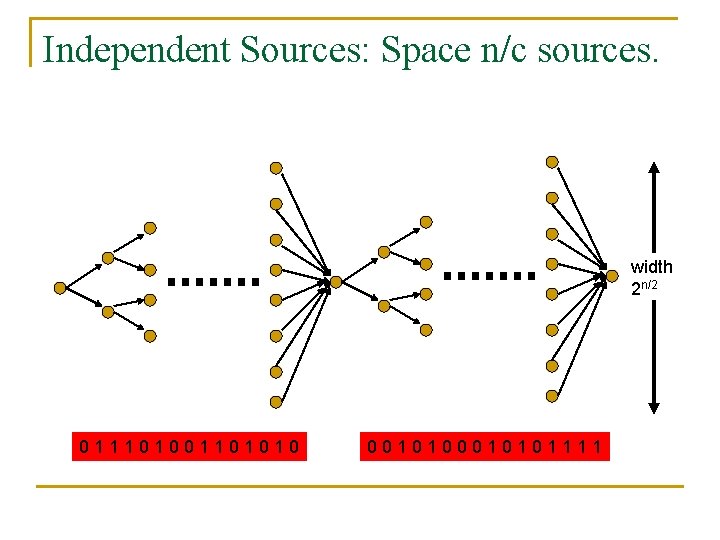
Small space sources capture: n n n Bit fixing sources: can be modeled by space 0 sources General Sources with min-entropy k: space k sources Independent sources: c independent sources can be modeled by space n/c sources

Bit Fixing Sources can be modelled by Space 0 sources 0. 5, 1 1, 1 0. 5, 0 ? 0. 5, 0 1 ? 1, 0 1, 1 0. 5, 0 ?

General Sources are Space n sources 1 , ] =1 [X 2 r P [X 1 r P Pr[ X 1 ], 1 1 = Pr[X 2 |X 1 1 = = 0|X 1 =1], width 2 n 0 =0 ], 0 Min-entropy k sources are convex combinations of space k sources n layers X= X 1 X 2 X 3 X 4 X 5 …. . …………. .

Independent Sources: Space n/c sources. width 2 n/2 011101001101010 0010101111

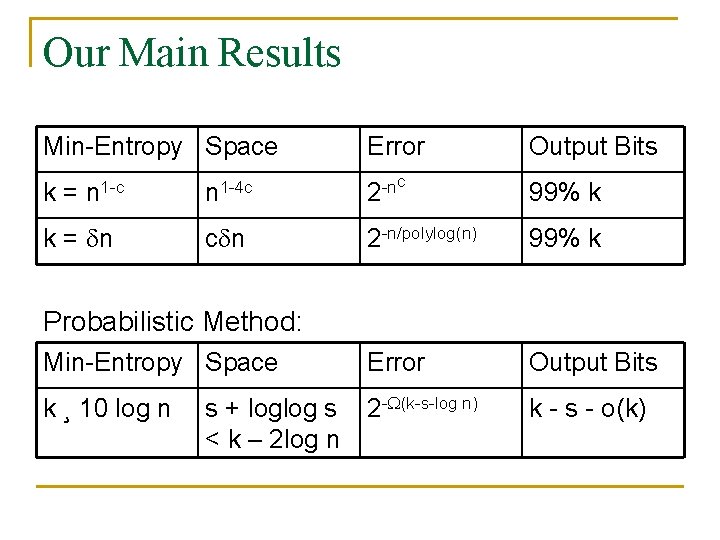
Our Main Results Min-Entropy Space Error Output Bits n 1 -4 c c -n 2 99% k c n 2 -n/polylog(n) 99% k Min-Entropy Space Error Output Bits k ¸ 10 log n 2 - (k-s-log n) k - s - o(k) k= n 1 -c k = n Probabilistic Method: s + loglog s < k – 2 log n

Outline The problem and results n Our Techniques n Extractor for linear min-entropy rate q Extractor for polynomial min-entropy rate q n Open Problems

We reduce to another model n Total Entropy k independent sources:

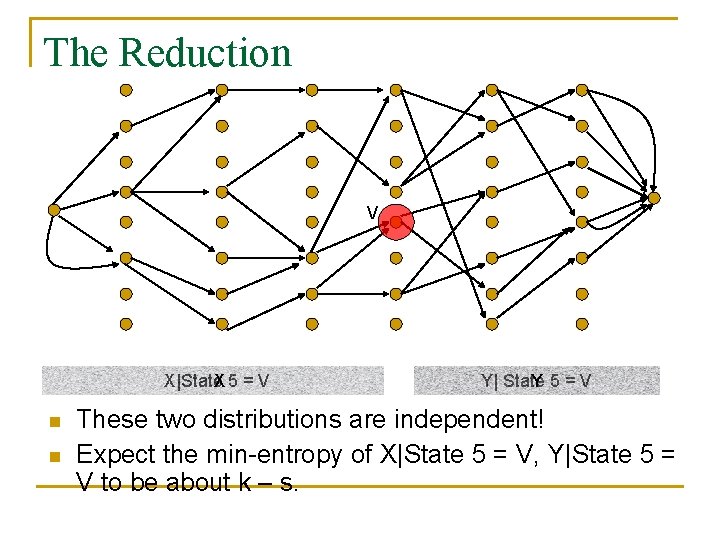
The Reduction V X|State X 5 = V n n Y| State Y 5=V These two distributions are independent! Expect the min-entropy of X|State 5 = V, Y|State 5 = V to be about k – s.

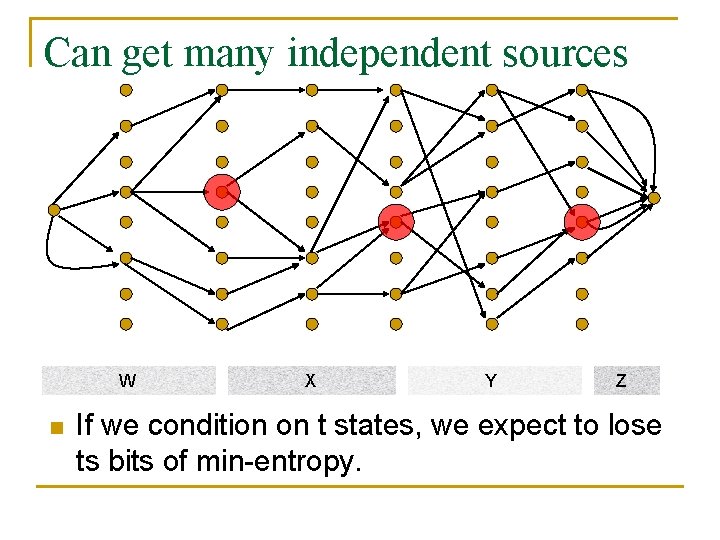
Can get many independent sources W n X Y Z If we condition on t states, we expect to lose ts bits of min-entropy.

Entropy Loss n n Let S 1, …, St denote the random variables for the state in the t layers. Pr[X = x] = Pr[X=x|S 1=s 1, …, St=st] Pr[S 1=s 1, …, St=st] X|S 1=s 1, …, St=st has min-entropy < k – 100 ts ) Pr[S 1 = s 1, …, St=st] < 2 -99 ts

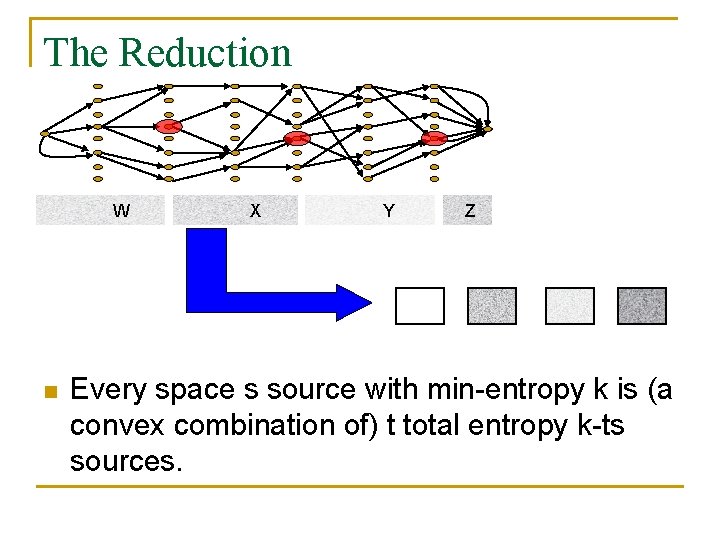
The Reduction W n X Y Z Every space s source with min-entropy k is (a convex combination of) t total entropy k-ts sources.

Some Additive Number Theory n [Bourgain, Glibichuk, Konyagin] For every constant < 1 there is are integers c 1( ), c 2( ) s. t. for every non-trivial additive character of GF(2 p) and every independent min-entropy p sources X 1, …, Xc 1( ), | E[ ( X 1 X 2 … Xc 1( ))] | < 2 -c 2( )p

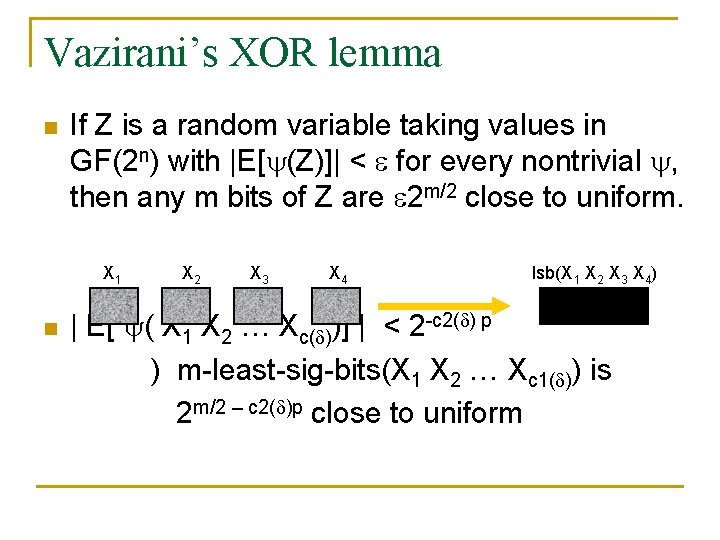
Vazirani’s XOR lemma n If Z is a random variable taking values in GF(2 n) with |E[ (Z)]| < for every nontrivial , then any m bits of Z are 2 m/2 close to uniform. X 1 n X 2 X 3 X 4 lsb(X 1 X 2 X 3 X 4) | E[ ( X 1 X 2 … Xc( ))] | < 2 -c 2( ) p ) m-least-sig-bits(X 1 X 2 … Xc 1( )) is 2 m/2 – c 2( )p close to uniform

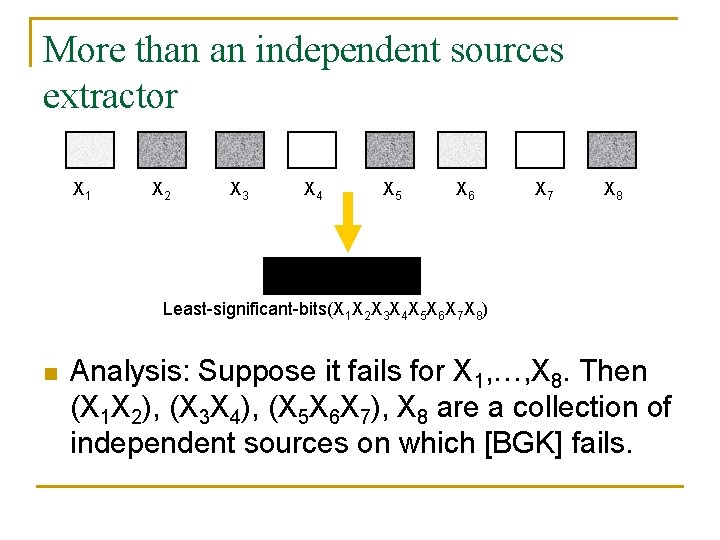
More than an independent sources extractor X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 Least-significant-bits(X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8) n Analysis: Suppose it fails for X 1, …, X 8. Then (X 1 X 2), (X 3 X 4), (X 5 X 6 X 7), X 8 are a collection of independent sources on which [BGK] fails.

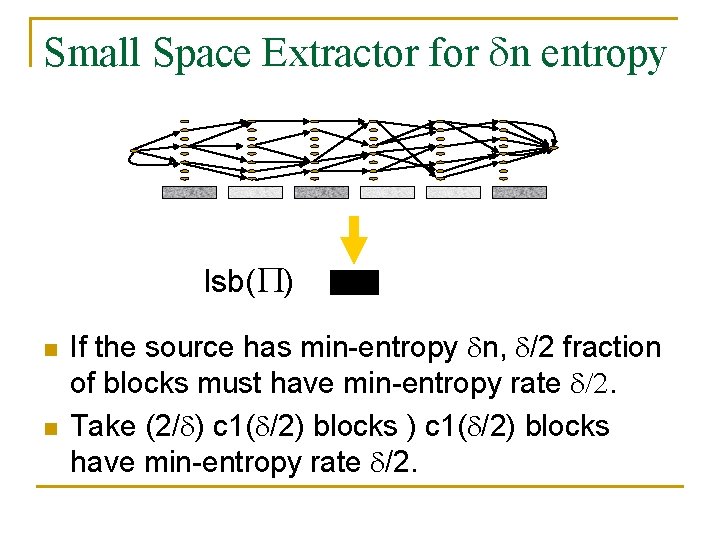
Small Space Extractor for n entropy lsb( ) n n If the source has min-entropy n, /2 fraction of blocks must have min-entropy rate /2. Take (2/ ) c 1( /2) blocks have min-entropy rate /2.

Result Theorem: For every > 0, there is an > 0 and a polynomial time computable extractor for min-entropy n, space n sources that extracts a linear fraction of the min-entropy with exponentially small error. Can improve to get 99% of the min-entropy out using techniques from [Gabizon, Raz, Shaltiel]

Outline The problem and results n Our Techniques n Extractor for linear min-entropy rate q Extractor for polynomial min-entropy rate q n Open Problems

For Polynomial Entropy Rate Black Boxes: n Good Condensers: [Barak, Kindler, Shaltiel, Sudakov, Wigderson], [Raz] n Good Mergers: [Raz], [Dvir, Raz] White Boxes: n Condensing somewhere random sources: [R. ]

Somewhere Random Sources Def: [TS 96] A source is somewhere-random if it has some uniformly random row. r t

Aligned Somewhere High Entropy Sources Def: Two somewhere high-entropy sources are aligned if the same row has high entropy in both sources.

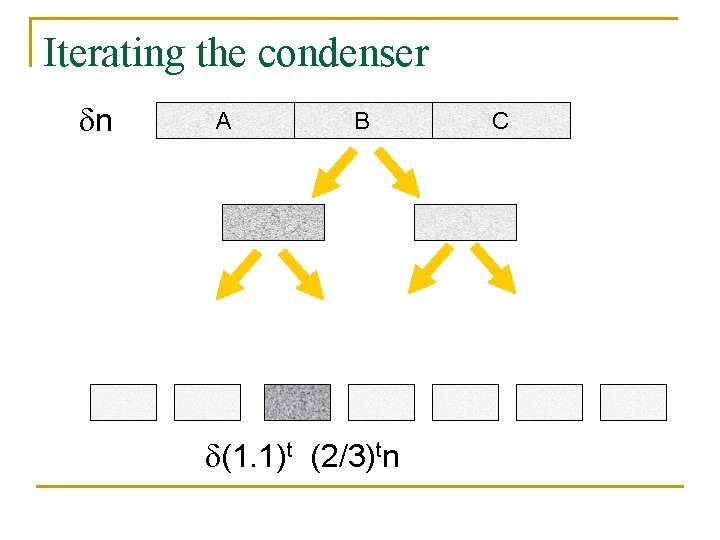
Condensers [BKSSW], [Raz], [Zuckerman] Elements in a prime field n A A B B (1. 1) (2 n/3) C C AC+B

Iterating the condenser n A B (1. 1)t (2/3)tn C

Mergers [Raz], [Dvir, Raz] 0. 9 C 99% of rows in output have entropy rate 0. 9

Condense + Merge [Raz] 1. 1 Condense 99% of rows in output have entropy rate 1. 1 Merge C

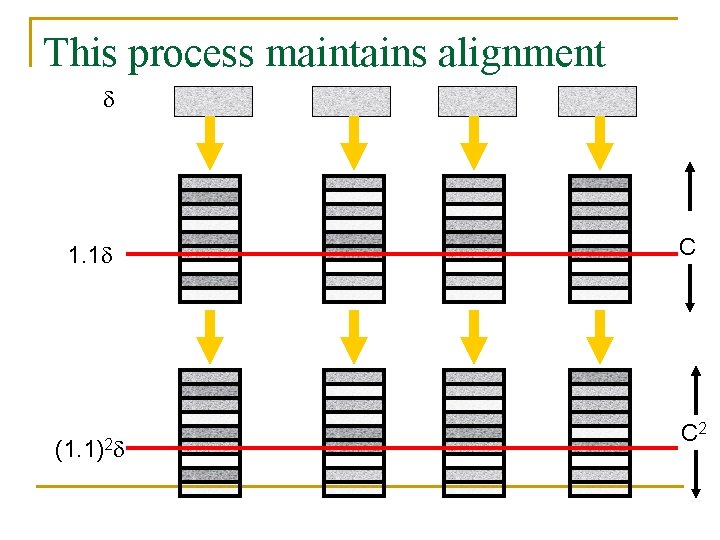
This process maintains alignment 1. 1 (1. 1)2 C C 2

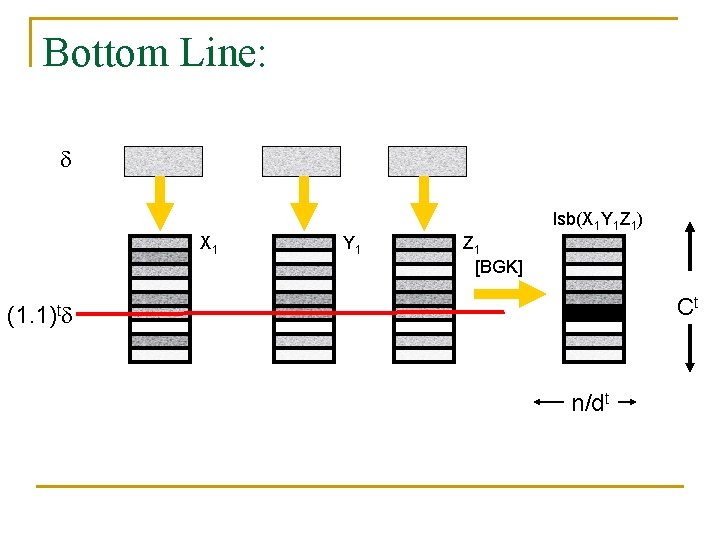
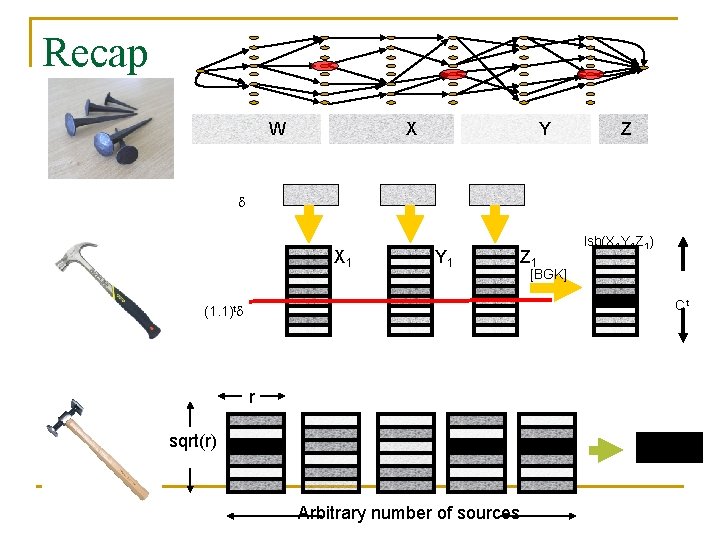
Bottom Line: lsb(X 1 Y 1 Z 1) X 1 Y 1 Z 1 [BGK] Ct (1. 1)t n/dt

Extracting from SR-sources [R. ] r sqrt(r) We generalize this: r sqrt(r) Arbitrary number of sources

Recap W X Y Z X 1 Y 1 Z 1 lsb(X 1 Y 1 Z 1) [BGK] Ct (1. 1)t r sqrt(r) Arbitrary number of sources

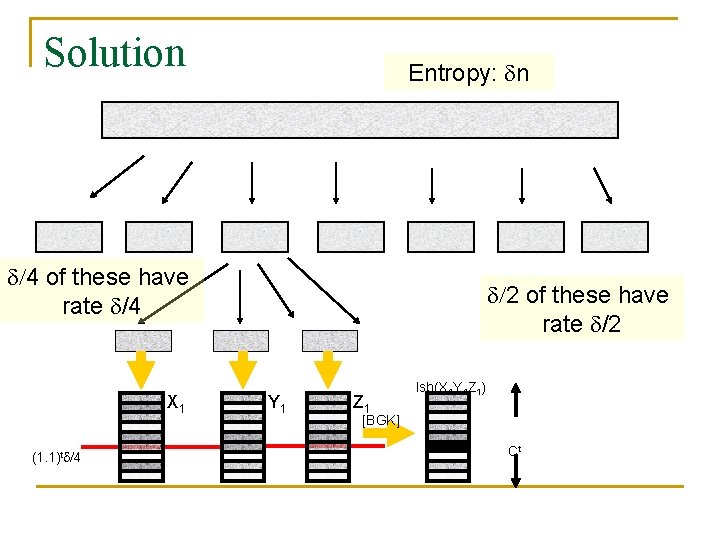
Solution Entropy: n /4 of these have rate /4 X 1 (1. 1)t /4 /2 of these have rate /2 Y 1 Z 1 lsb(X 1 Y 1 Z 1) [BGK] Ct

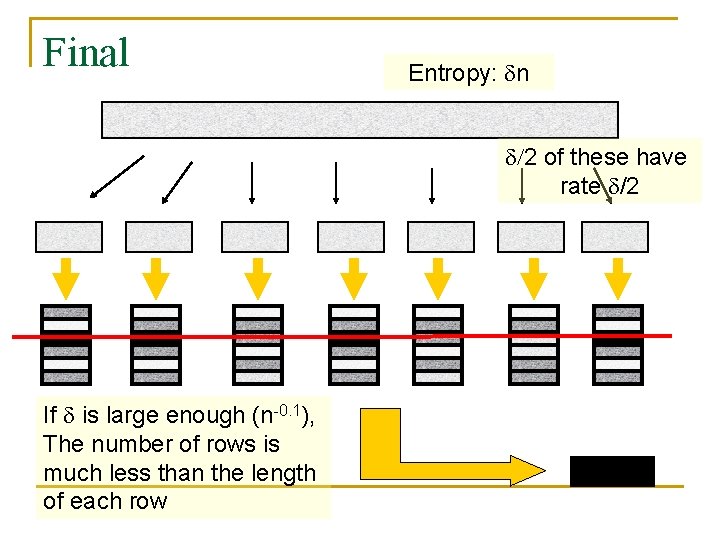
Final Entropy: n /2 of these have rate /2 If is large enough (n-0. 1), The number of rows is much less than the length of each row

Result Theorem: (Assuming we can find primes), there is a constant s. t. we can extract from space n 1 -2 min-entropy n 1 - sources (1) -n with error 2 Can improve to get 99% of the min-entropy out using techniques from [Gabizon, Raz, Shaltiel]

Outline The problem and results n Our Techniques n Extractor for linear min-entropy rate q Extractor for polynomial min-entropy rate q n Open Problems

Open Problems Better Extractors for small space n Other models? n

Questions?