Deterministic counting algorithms Counting via dynamic programming not

Deterministic counting algorithms Counting via dynamic programming [not in the book]: - e. g. , counting the number of increasing subsequences [Chapter 1]

Deterministic counting algorithms Counting via dynamic programming [not in the book]: - e. g. , counting the number of increasing subsequences [Chapter 1]

From counting to sampling [Chapter 1] Sampling increasing subsequences uniformly at random ?

Perfect matchings in planar graphs Counting problem definition: [Section 1. 2]

Perfect matchings in planar graphs Let M, M’ be two perfect matchings. What does M [ M’ look like ? [Section 1. 2]

Perfect matchings in planar graphs [Section 1. 2] Def: Let G be an orientation of G and let C be an even cycle of G. C is oddly oriented by G if an odd # of edges in C disagrees with G. G is Pfaffian if, for every perfect matchings M, M’, every cycle in M [ M’ is oddly oriented. Note: not every cycle in G, just every cycle in M [ M’.

Perfect matchings in planar graphs [Section 1. 2] Def: Skew adjacency matrix of G is As(G ) where aij = +1 if (i, j) is an edge in G -1 if (j, i) is an edge in G 0 otherwise

Perfect matchings in planar graphs [Section 1. 2] Thm 1. 11 Kasteleyn): ( For any Pfaffian orientation G , # perfect matchings of G = det As(G ) Thm 1. 14: Every planar graph has a Pfaffian orientation (and it can be easily constructed). Note: It is not known whether the problem of deciding if a graph has a Pfaffian orientation is in P nor whether it is NPcomplete.

Determinants, etc. [Section 1. 2] Def: The determinant of an nxn matrix A is: det(A) = ¼ 2 Sn sgn(¼) i=1, …, n ai, ¼(i), where Sn is the set of all permutations of {1, …, n} and sgn(¼) is the sign of the permutation ¼.

Determinants, etc. [Section 1. 2] Def: The permanent of an nxn matrix A is: perm(A) = ¼ 2 Sn i=1, …, n ai, ¼(i), where Sn is the set of all permutations of {1, …, n}. Note: - if A is an adjacency matrix of a bipartite graph, the permanent computes the number of perfect matchings - determinant can be computed in polynomial time, permanent is #P-complete !

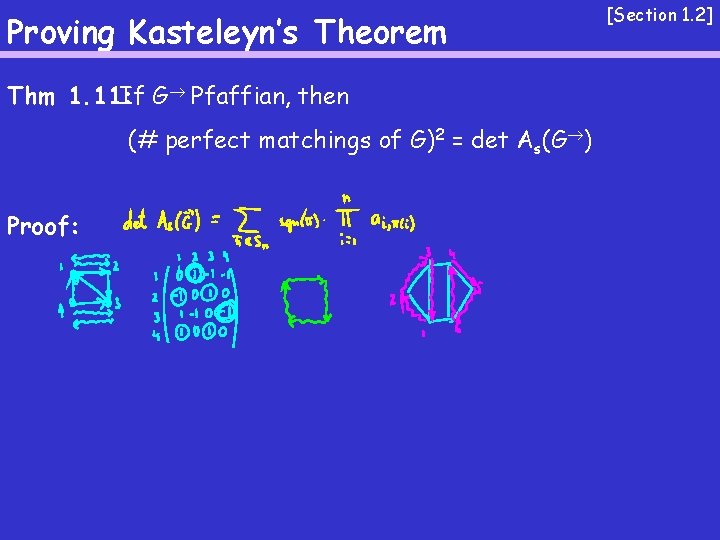
Proving Kasteleyn’s Theorem Thm 1. 11: If G Pfaffian, then (# perfect matchings of G)2 = det As(G ) Proof: [Section 1. 2]

Pfaffian orientations in planar graphs [Section 1. 2] Lemma 1. 13: Let G be a connected planar digraph (drawn in plane) with all faces except outer having an odd number of clockwise oriented edges. Then, in any (simple) cycle C, the number of clockwise edges is opposite parity as the number of vertices inside C. In particular, G from Lemma 1. 13 is Pfaffian.

Pfaffian orientations in planar graphs [Section 1. 2] Lemma 1. 13: Let G be a connected planar digraph (drawn in plane) with all faces except outer having an odd number of clockwise oriented edges. Then, in any (simple) cycle C, the number of clockwise edges is opposite parity as the number of vertices inside C. Proof: Let v = # vertices inside C k = length of C c = # clockwise edges in C f = # faces inside C e = # edges inside C ci = # clockwise edges in component i inside C

Pfaffian orientations in planar graphs [Section 1. 2] Thm 1. 14: Every planar graph has a Pfaffian orientation. Proof:

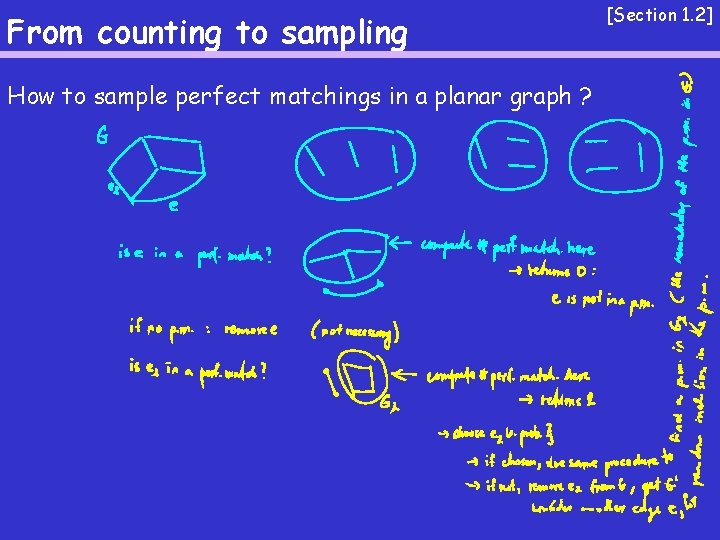
From counting to sampling How to sample perfect matchings in a planar graph ? [Section 1. 2]