Determining the Significance of Experimental Results Identifying Treatment

Determining the Significance of Experimental Results

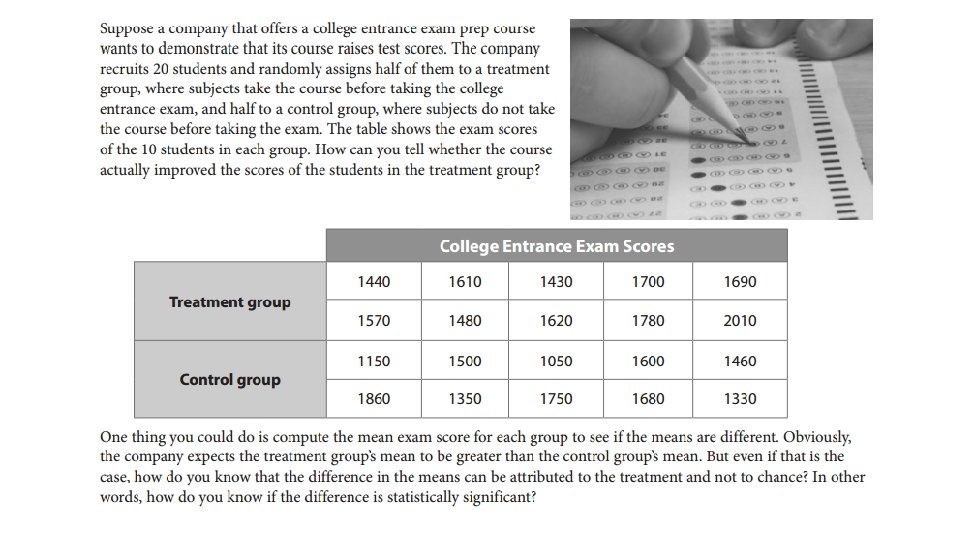
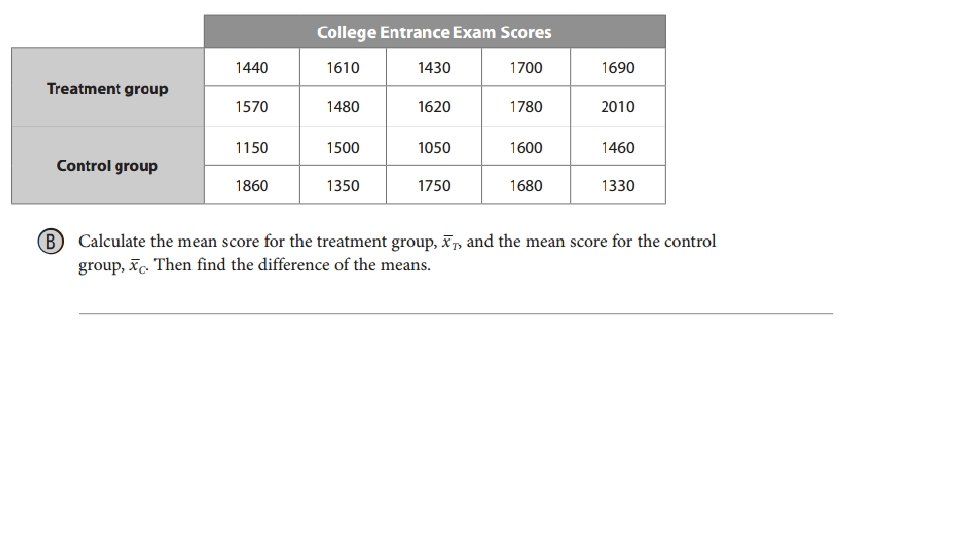
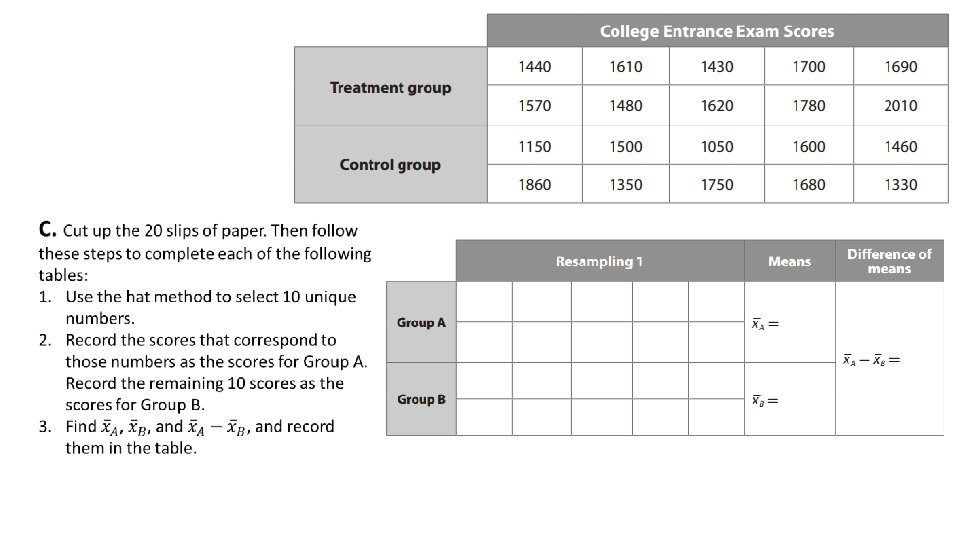
Identifying Treatment and Control Groups • Whether a study is observational or experimental, it should be comparative in order to establish a connection between the factor/treatment and the characteristic of interest. • Ex: Determining the rate of car accidents among people who talk on cell phones while driving is not instructive unless you compare it with the rate of car accidents among people who don’t talk on cell phones while driving and find that it is statistically different. • While a comparative observational study can suggest a relationship between two variables, such as cell phone use while driving and car accidents, it cannot establish a cause-and-effect relationship because there can be confounding variables (also called lurking variables) that influence the results. • Ex: Perhaps people who talk on cell phones while driving are more likely to drive aggressively, so it is aggressive driving (not the cell phone use) that leads to a higher rate of car accidents. • In an experiment, randomization can remove the problem of a confounding variable by distributing the variable among the groups being compared so that its influence on the groups is more or less equal. Therefore, the best way to establish a cause-and-effect relationship between two variables is through a randomized comparative experiment where subjects are randomly divided into two groups: the treatment group, which is given the treatment, and the control group, which is not.

Ex:

Ex:

Your Turn:

Formulating the Null Hypothesis • You can think of every randomized comparative experiment as a test of a null hypothesis. The null hypothesis states that any difference between the control group and the treatment group is due to chance. In other words, the null hypothesis is the assumption that the treatment has no effect. • Statistically significant results are large difference in results between the treatment group and the control group. • A statistically significant result does not prove that the treatment has an effect; the null hypothesis may still be true, and a rare event may simply have occurred. Nevertheless, standard practice in statistics is to reject the null hypothesis in favor of the alternative hypothesis that the result is, in fact, due to the treatment.

Ex:

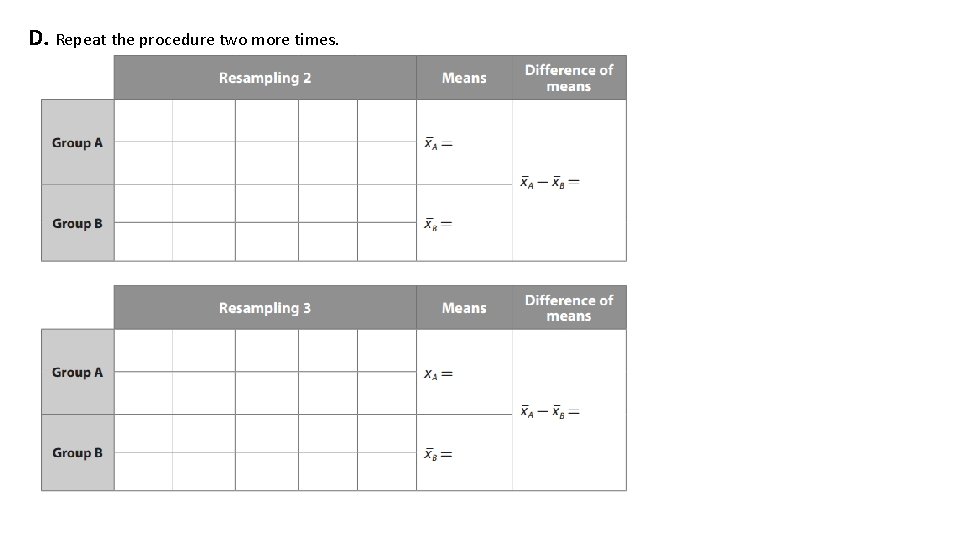
D. Repeat the procedure two more times.

E.

Statistical Significance • Statistically significant results are large difference in results between the treatment group and the control group. • An unusual experimental result may be statistically significant. Statistically significant results imply that the difference in results between the means of the treatment group and the control group were unlikely due to chance.

Ex: Researchers randomly select 9 students who are given breakfast and 9 students who are not. Each group takes an 80 question math test 1 hour after the students in the treatment group eat breakfast, and the researchers record the number of questions each student answers correctly. The data are shown in the table. Resampling the data finds that 95% of the differences of the means for the reconfigured treatment and control groups are less than 5. 2. (Note that resampling involves randomly scrambling the data from the treatment and control groups and calculating a difference of means for the reconfigured groups: treatment group mean minus control group mean. Each new difference obtained from a resampling becomes part of a resampling distribution. ) Is there evidence that eating breakfast increases performance on the math test? a) Yes; the difference of the means from the experiment is greater than 5. 2. b) Yes; the difference of the means from the experiment is less than 5. 2. c) No; the difference of the means from the experiment is greater than 5. 2. d) No; the difference of the means from the experiment is less than 5. 2.

Essential Question: Explain how a simulation can determine statistical significance between the means of two groups. __________________________________________________________