Determining the Key Features of Function Graphs The

Determining the Key Features of Function Graphs

The Key Features of Function Graphs - Preview p Domain and Range p x-intercepts and y-intercepts p Intervals of increasing, decreasing, and constant behavior p Parent Equations p Maxima and Minima

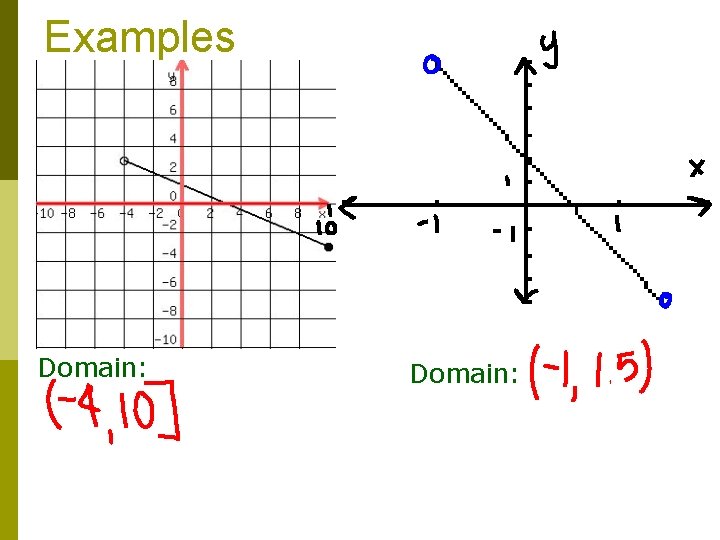
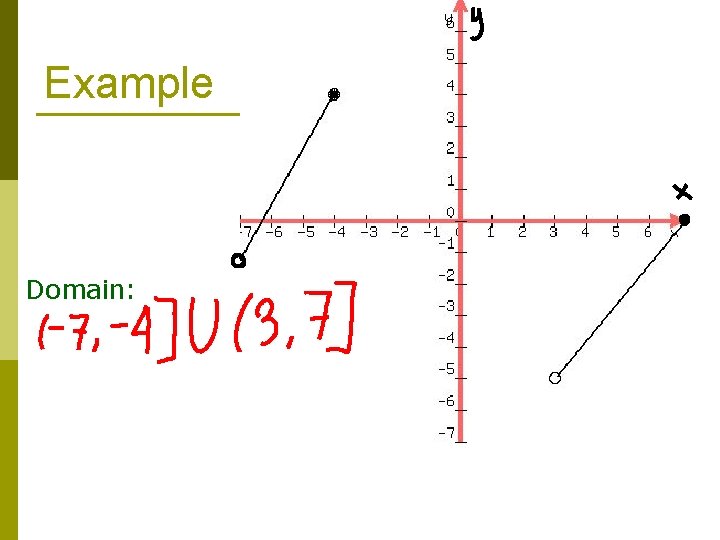
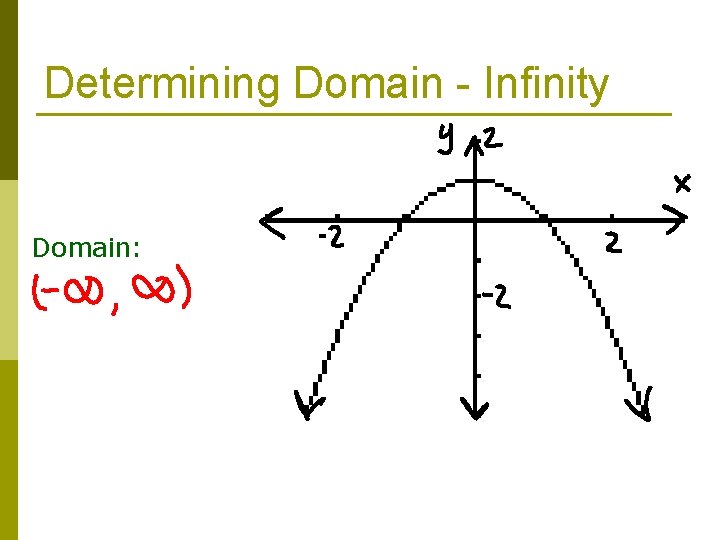
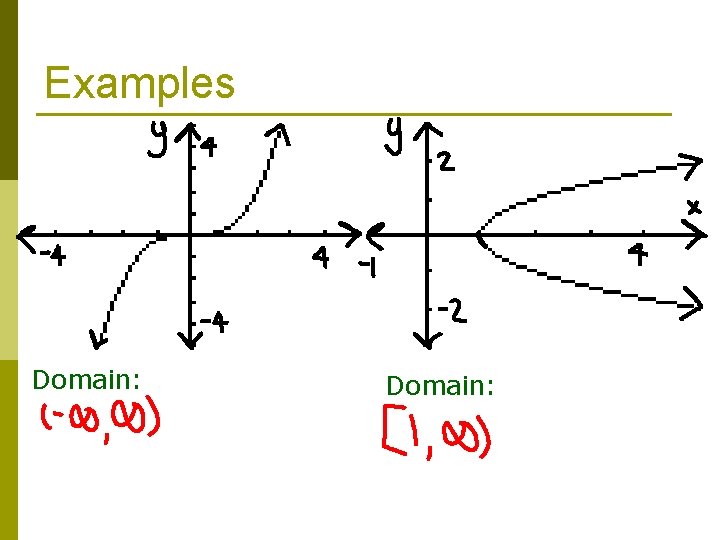
Domain p Domain is the set of all possible input or x-values p To find the domain of the graph we look at the x-axis of the graph

Determining Domain - Symbols p Open Circle → p Exclusive p( ) p Closed Circle → p Inclusive p[ ]

Identifying the Domain 1. 2. 3. Start at the far left of the graph. Move along the x-axis until you find the lowest possible x-value of the graph. This is your lower bound. Note if you have a open circle or a closed circle. Keep moving along the x-axis until you find your highest possible x-value of the graph. This is your upper bound. Note if you have a open circle or a closed circle.

Examples Domain:

Example Domain:

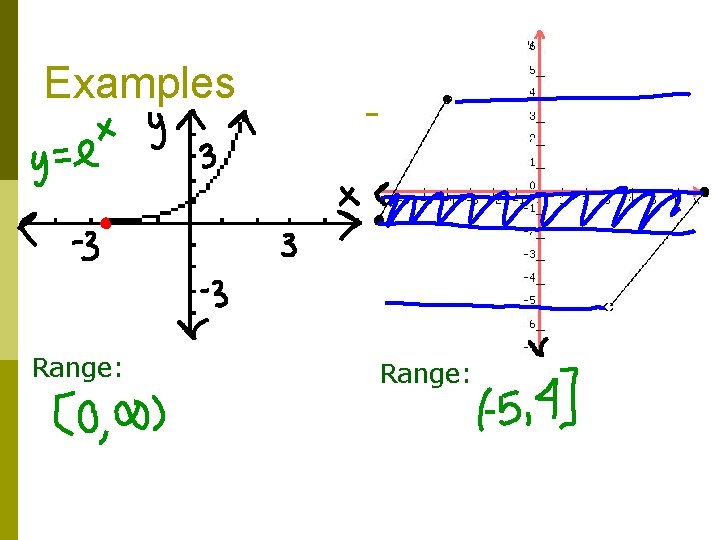
Determining Domain - Infinity Domain:

Examples Domain:

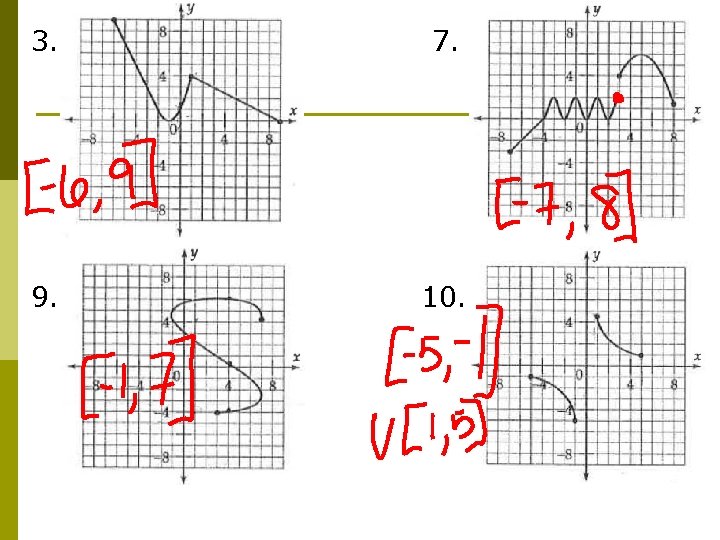
Your Turn: p Complete problems 3, 7, and find the domain of 9 and 10 on pg. 160 from the Xeroxed sheets 3. 7. 9. 10.

3. 7. 9. 10.

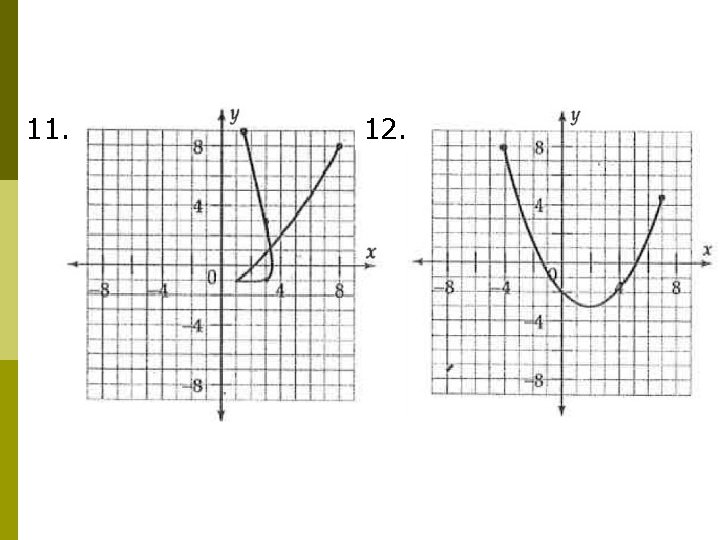
11. 12.

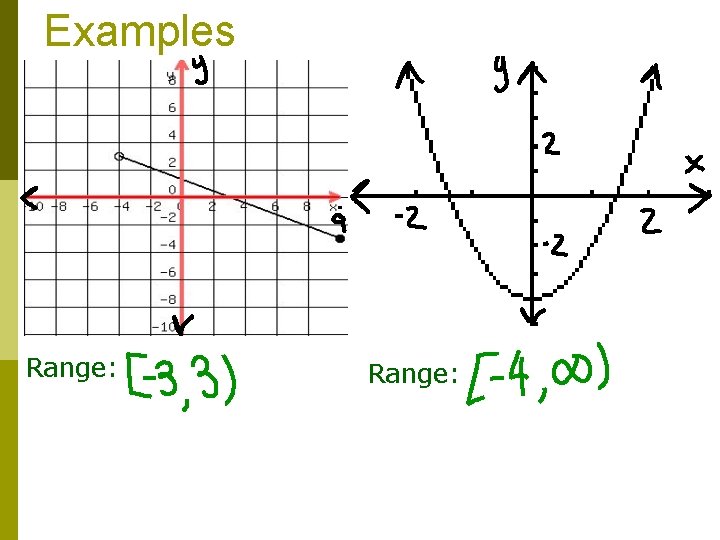
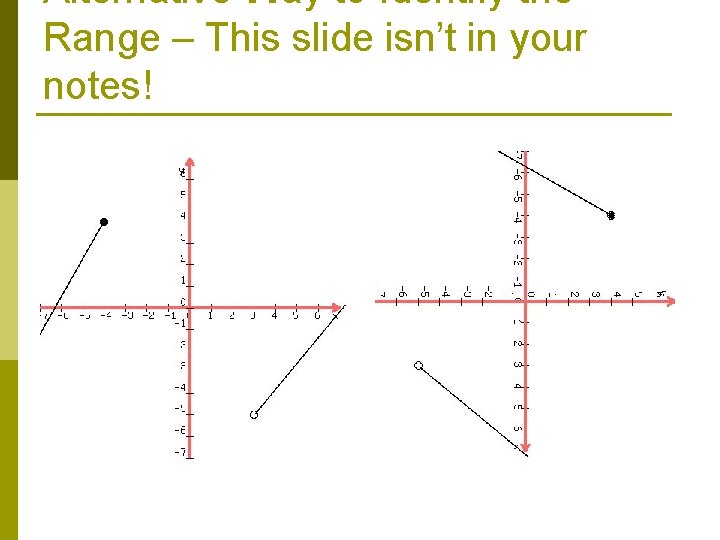
Range p The set of all possible output or yvalues p To find the range of the graph we look at the y-axis of the graph p We also use open and closed circles for the range

***Identifying the Range 1. 2. 3. Start at the bottom of the graph. Move along the y-axis until you find the lowest possible y-value of the graph. This is your lower bound. Note if you have a open circle or a closed circle. Keep moving along the y-axis until you find your highest possible y-value of the graph. This is your upper bound. Note if you have a open circle or a closed circle.

Examples Range:

Examples Range:

Alternative Way to Identify the Range – This slide isn’t in your notes!

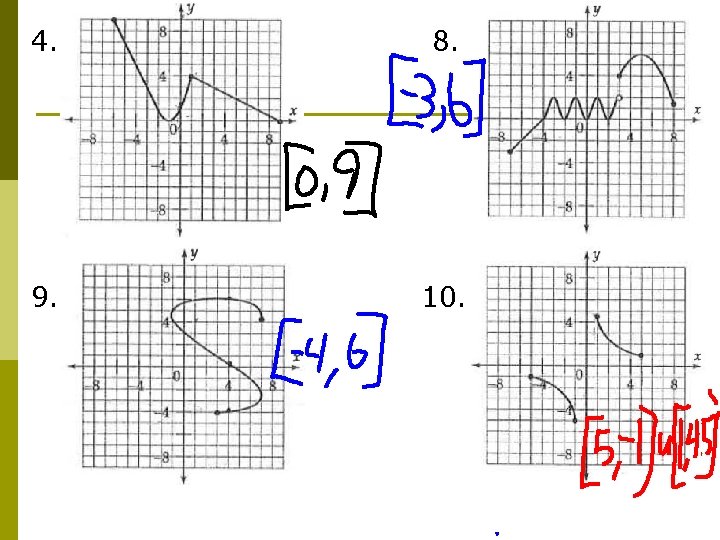
Your Turn: p Complete problems 4, 8, and find the range of 9 and 10 on pg. 160 from the Xeroxed sheets 4. 8. 9. 10.

4. 8. 9. 10.

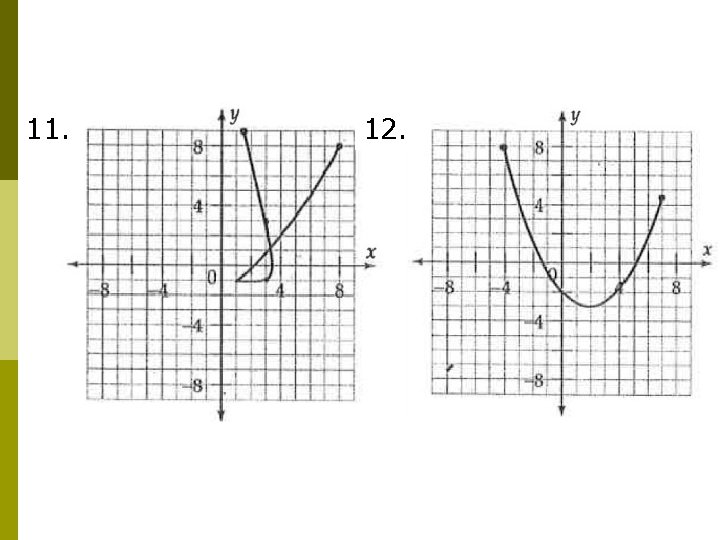
11. 12.

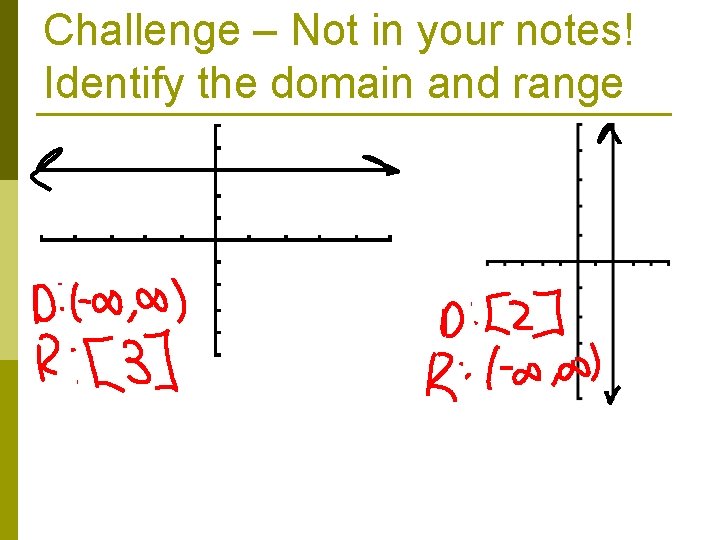
Challenge – Not in your notes! Identify the domain and range

X-Intercepts Where the graph crosses the x-axis p Has many names: p n n n x-intercept Roots Zeros

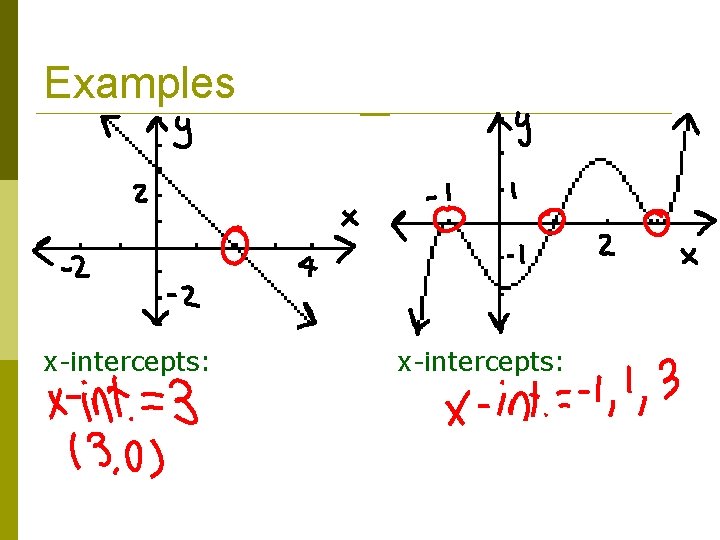
Examples x-intercepts:

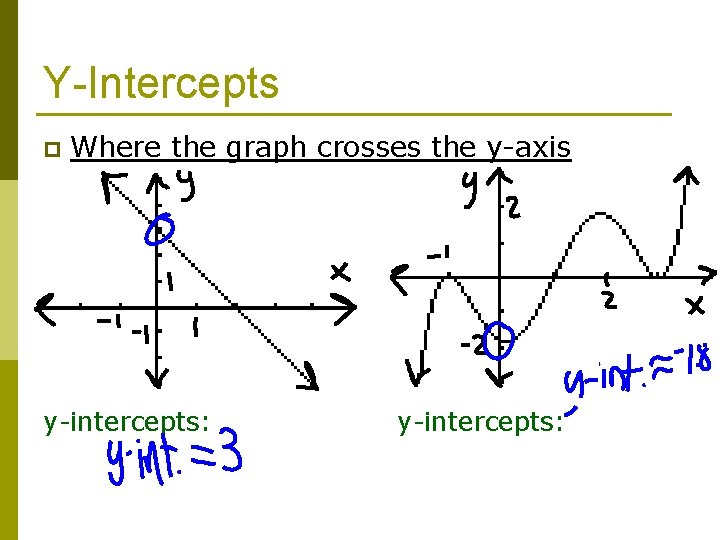
Y-Intercepts p Where the graph crosses the y-axis y-intercepts:

Seek and Solve!!!

Types of Function Behavior p 3 types: n n n p Increasing Decreasing Constant When determining the type of behavior, we always move from left to right on the graph

Roller Coasters!!! Fujiyama in Japan

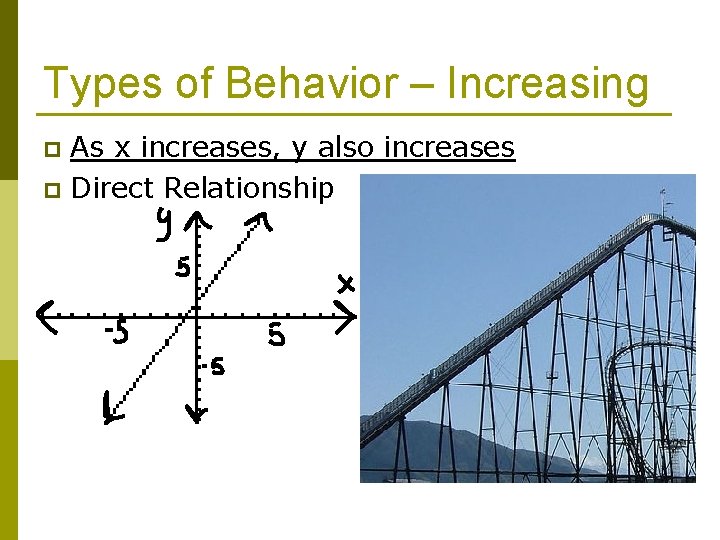
Types of Behavior – Increasing As x increases, y also increases p Direct Relationship p

Types of Behavior – Constant p As x increases, y stays the same

Types of Behavior – Decreasing As x increases, y decreases p Inverse Relationship p

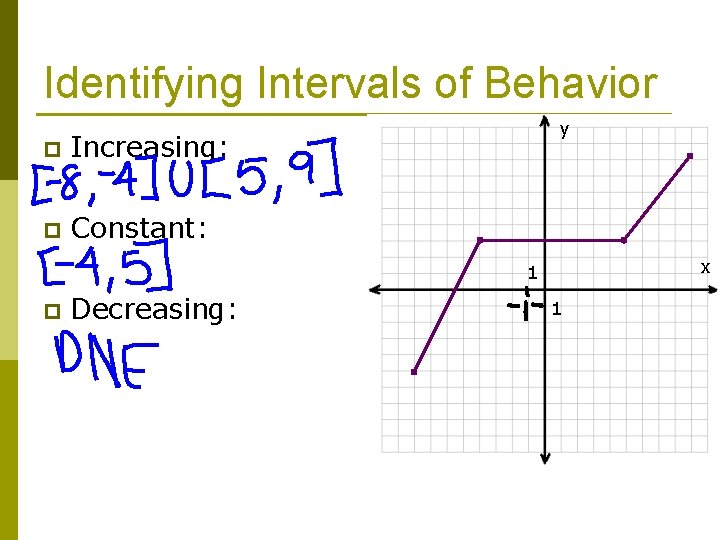
Identifying Intervals of Behavior We use interval notation p The interval measures x-values. The type of behavior describes y-values. Increasing: [0, 4) p The y-values are increasing when the x-values are between 0 inclusive and 4 exclusive

Identifying Intervals of Behavior p Increasing: p Constant: y x 1 p Decreasing: 1

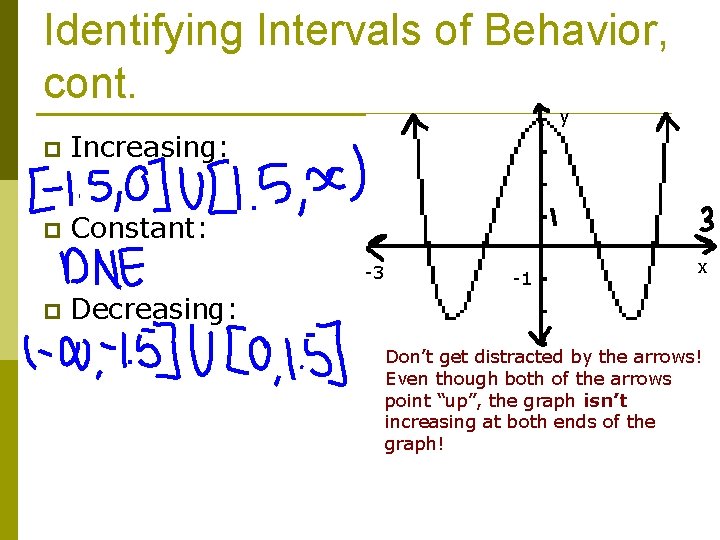
Identifying Intervals of Behavior, cont. y p Increasing: p Constant: -3 p -1 x Decreasing: Don’t get distracted by the arrows! Even though both of the arrows point “up”, the graph isn’t increasing at both ends of the graph!

Your Turn: p Complete problems 1 – 4 on The Key Features of Function Graphs – Part II handout.

1. 3. 2. 4.

What do you think of when you hear the word parent?

Parent Function The most basic form of a type of function p Determines the general shape of the graph p

Basic Types of Parent Functions 1. 2. 3. 4. Linear Absolute Value Greatest Integer Quadratic 5. 6. 7. 8. Cubic Square Root Cube Root Reciprocal

Parent Function Flipbook

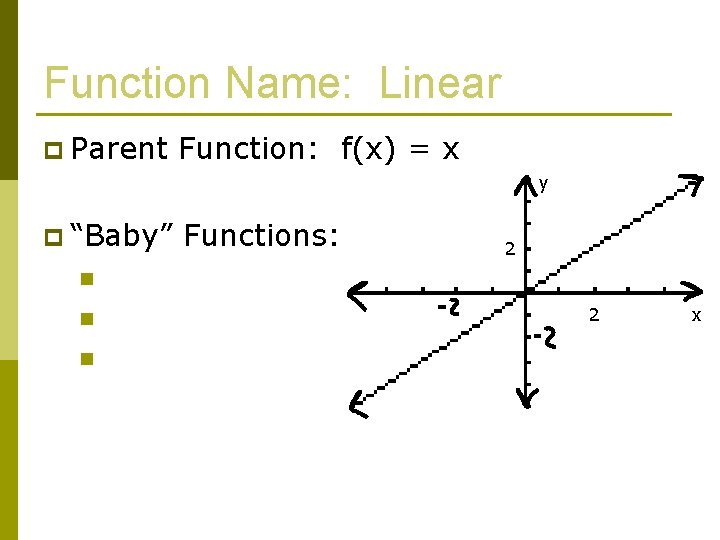
Function Name: Linear p Parent Function: f(x) = x y p “Baby” Functions: 2 n n n 2 x

Greatest Integer Function p f(x) = [[x]] p f(x) = int(x) p Rounding function n Always round down

“Baby” Functions p p Look and behave similarly to their parent functions To get a “baby” functions, add, subtract, multiply, and/or divide parent equations by (generally) constants n n n f(x) = x 2 f(x) = x 3 f(x) = 5 x 2 – 14 f(x) = -2 x 3 + 4 x 2 – x + 2

“Baby” Functions, cont. p f(x) = |x| p n n n

Your Turn: p Create your own “baby” functions in your parent functions book.

Identifying Parent Functions p From Equations: n Identify the most important operation 1. 2. 3. Special Operation (absolute value, greatest integer) Division by x Highest Exponent (this includes square roots and cube roots)

Examples 1. f(x) = x 3 + 4 x – 3 2. f(x) = -2| x | + 11 3.

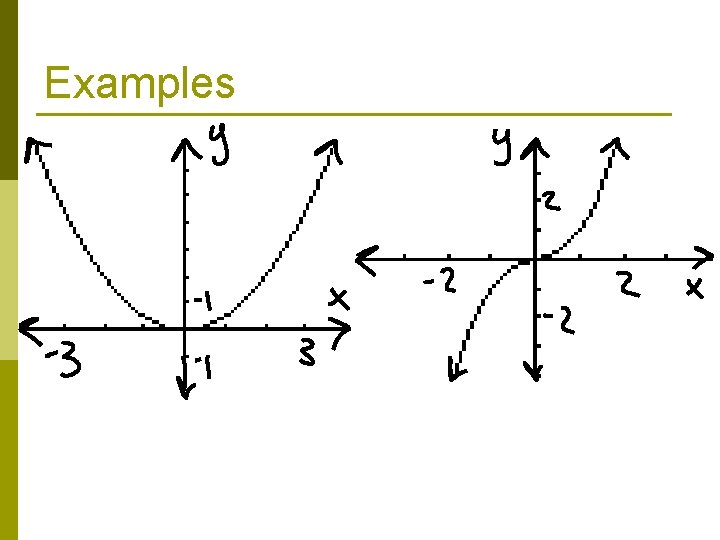
Identifying Parent Equations p From n Graphs: Try to match graphs to the closest parent function graph

Examples

Your Turn: p Complete problems 5 – 12 on The Key Features of Function Graphs handout

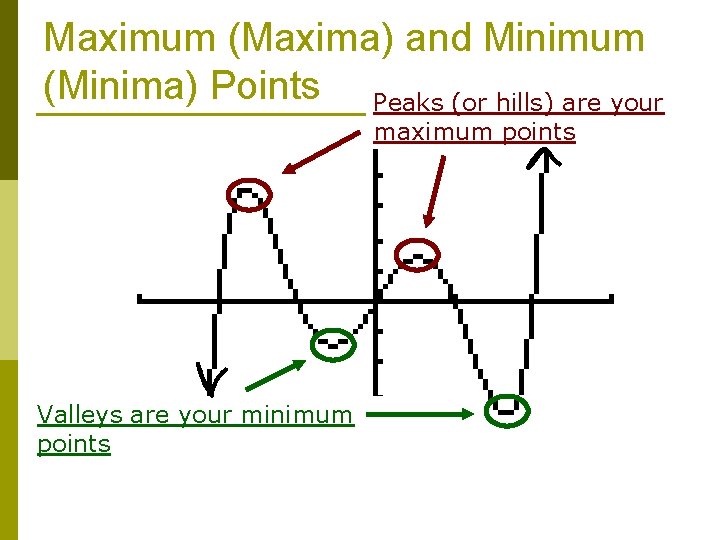
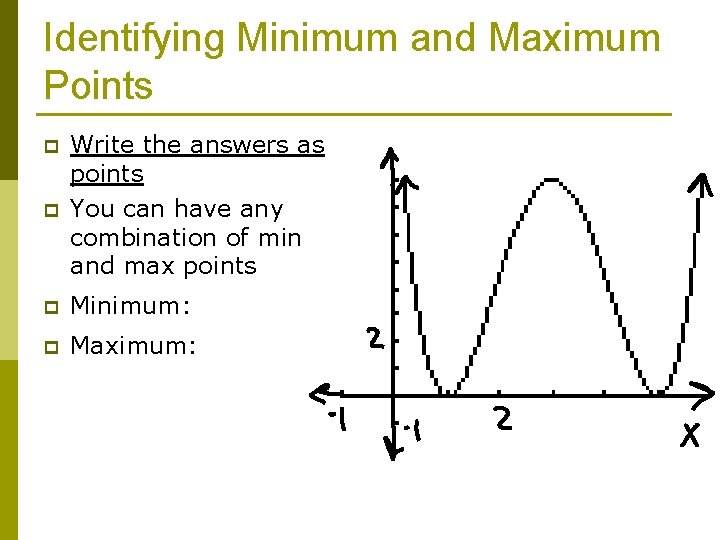
Maximum (Maxima) and Minimum (Minima) Points Peaks (or hills) are your maximum points Valleys are your minimum points

Identifying Minimum and Maximum Points p Write the answers as points You can have any combination of min and max points p Minimum: p Maximum: p

Examples

Your Turn: p Complete problems 1 – 6 on The Key Features of Function Graphs – Part III handout.

1. 2. 3. 4. 5. 6.

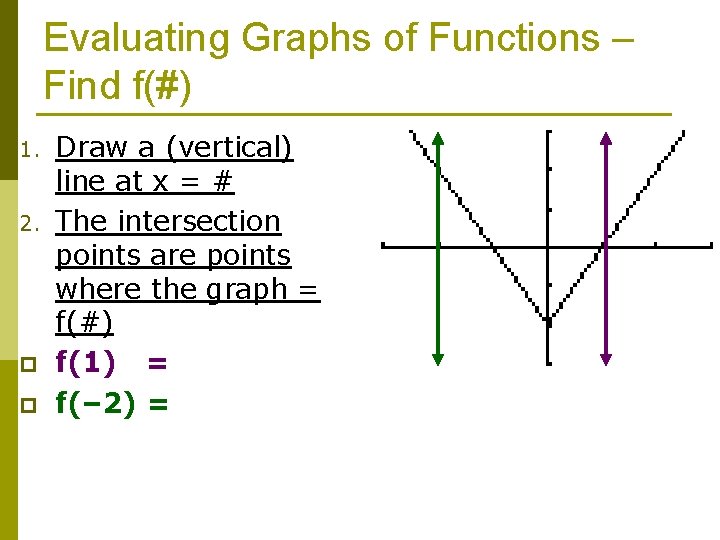
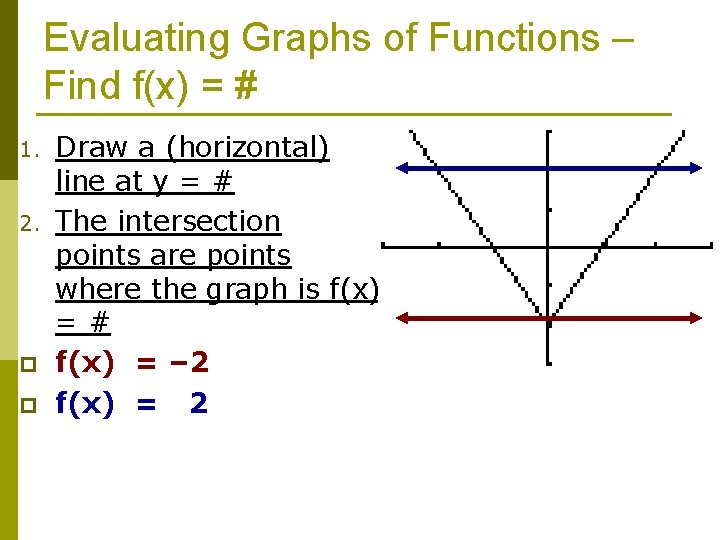
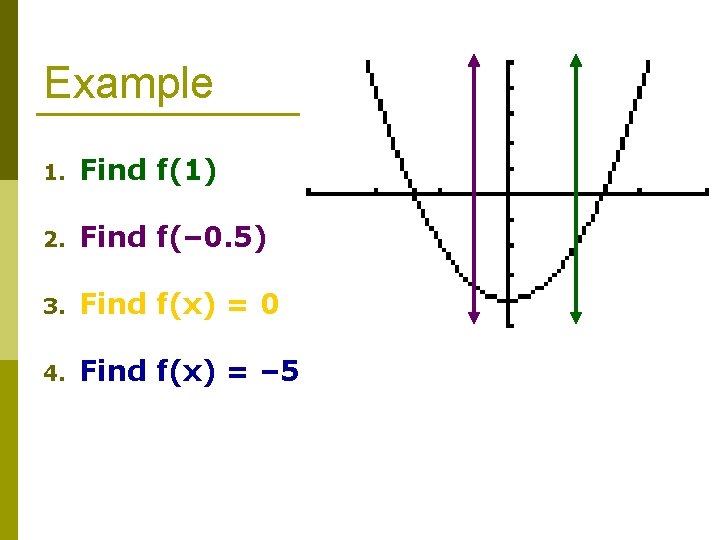
Reminder: Find f(#) and Find f(x) = x p Find f(#) n Find the value of f(x) when x equals #. n Solve for f(x) or y! p Find f(x) = # n Find the value of x when f(x) equals #. n Solve for x!

Evaluating Graphs of Functions – Find f(#) 1. 2. p p Draw a (vertical) line at x = # The intersection points are points where the graph = f(#) f(1) = f(– 2) =

Evaluating Graphs of Functions – Find f(x) = # 1. 2. p p Draw a (horizontal) line at y = # The intersection points are points where the graph is f(x) =# f(x) = – 2 f(x) = 2

Example 1. Find f(1) 2. Find f(– 0. 5) 3. Find f(x) = 0 4. Find f(x) = – 5

Your Turn: p Complete Parts A – D for problems 7 – 14 on The Key Features of Function Graphs – Part III handout.

7. 8. 9. 10.

11. 12. 13. 14.