Determining the Key Features of Function Graphs 10

Determining the Key Features of Function Graphs 10 February 2011

The Key Features of Function Graphs Preview p Domain p Intervals of increasing, p Range decreasing, and constant p x-intercepts behavior p y-intercept p Parent Equation p End Behavior p Maxima and Minima

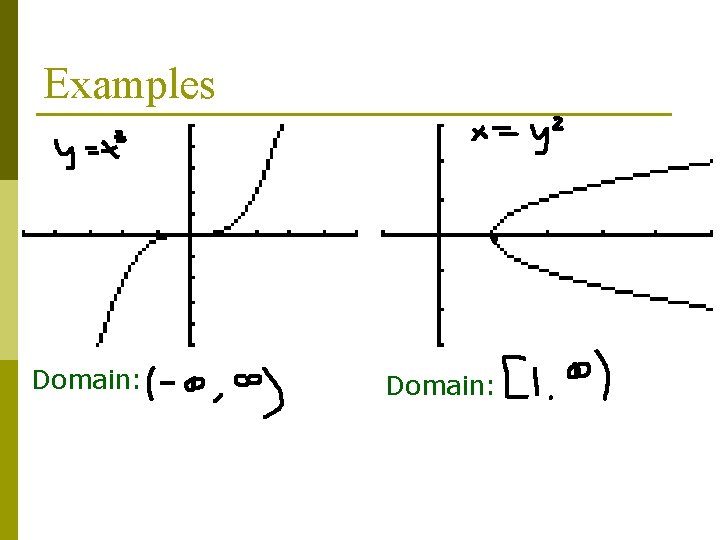
Domain p Reminder: Domain is the set of all possible input or x-values p When we find the domain of the graph we look at the x-axis of the graph

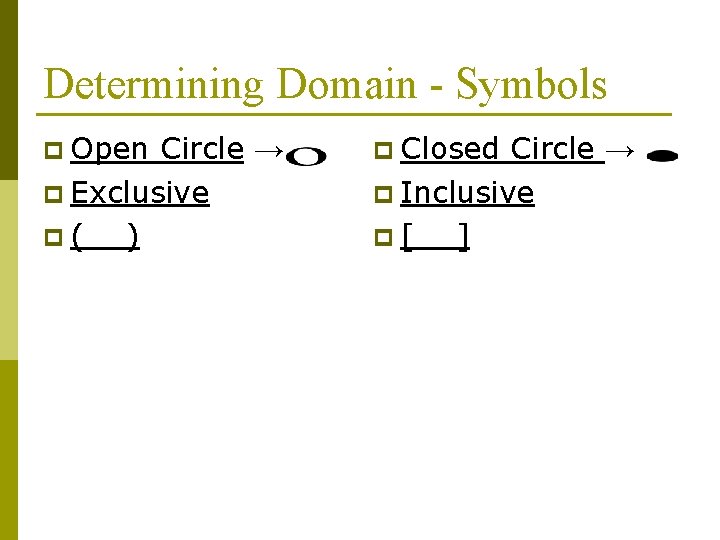
Determining Domain - Symbols p Open Circle → p Exclusive p( ) p Closed Circle → p Inclusive p[ ]

Determining Domain 1. 2. 3. 4. Start at the origin Move along the x-axis until you find the lowest possible x-value. This is your lower bound. Return to the origin Move along the x-axis until you find your highest possible x-value. This is your upper bound.

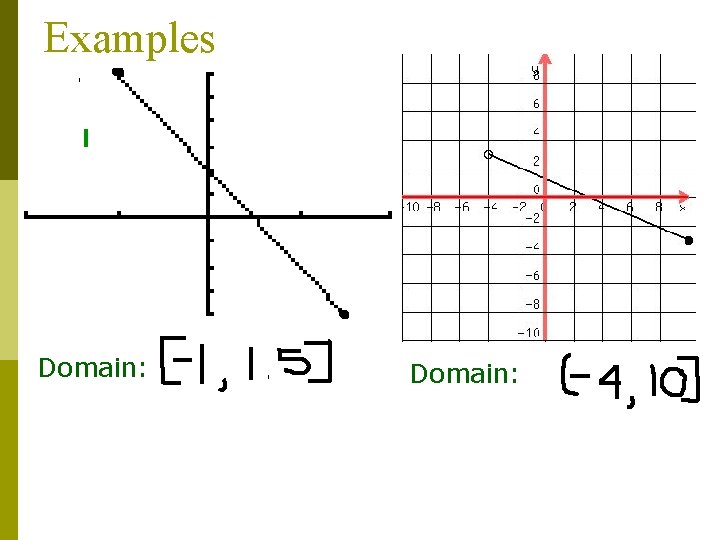
Examples Domain:

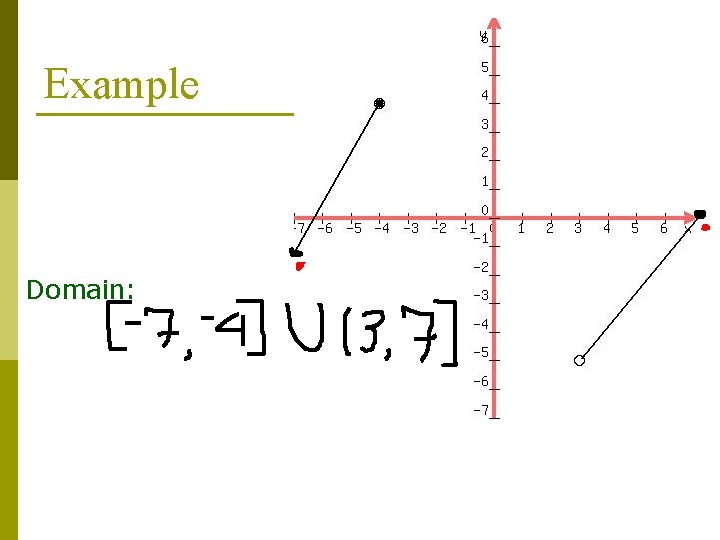
Example Domain:

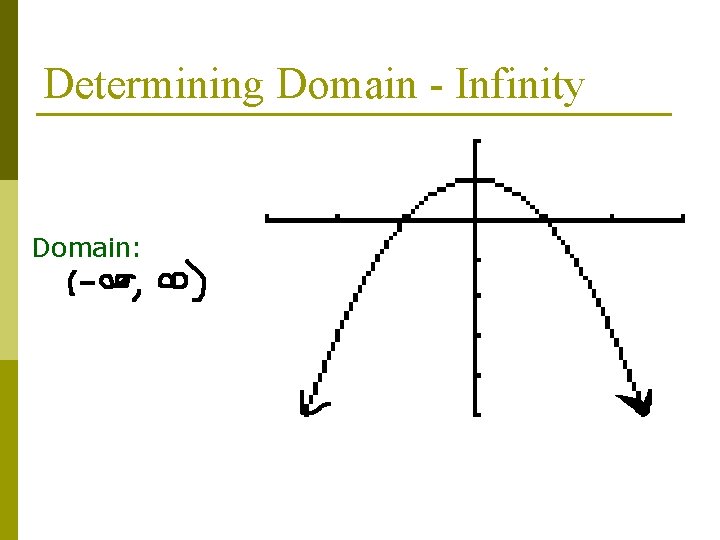
Determining Domain - Infinity Domain:

Examples Domain:

Your Turn: p In the purple Precalculus textbooks, complete problems 3, 7, and find the domain of 9 and 10 on pg. 160 3. 7. 9. 10.

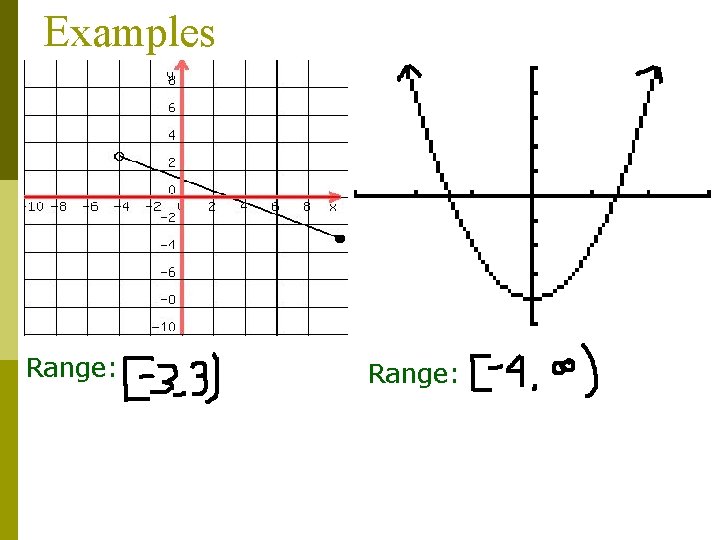
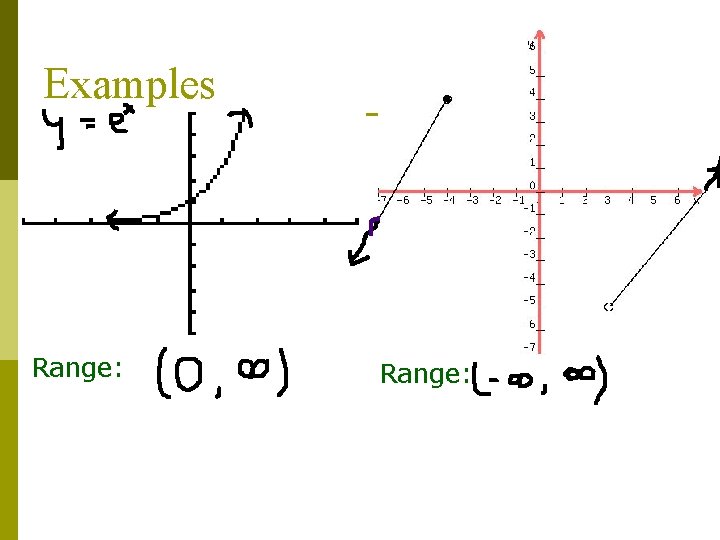
Range p The set of all possible output or yvalues p When we find the range of the graph we look at the y-axis of the graph p We also use open and closed circles for the range

Determining Range p p Start at the origin Move along the y-axis until you find the lowest possible y-value. This is your lower bound. Return to the origin Move along the y-axis until you find your highest possible y-value. This is your upper bound.

Examples Range:

Examples Range:

Your Turn: p In the purple Precalculus textbooks, complete problems 4, 8, and find the domain of 9 and 10 on pg. 160 4. 8. 9. 10.

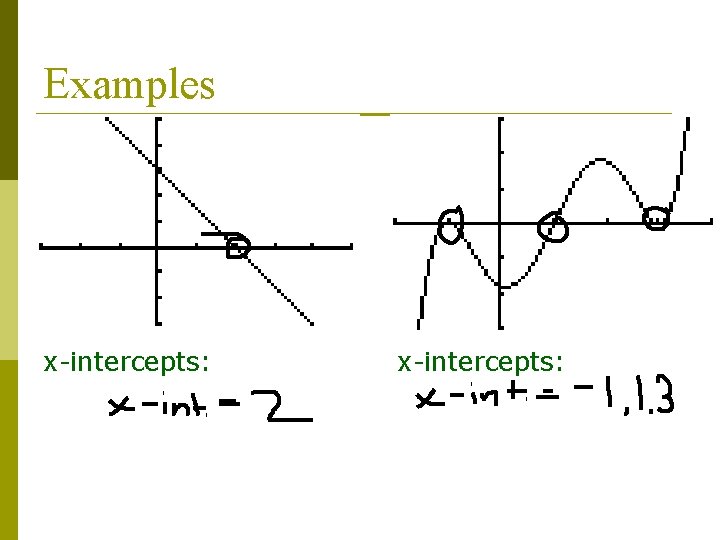
X-Intercepts Where the graph crosses the x-axis p Has many names: p n n n x-intercept Roots Zeros

Examples x-intercepts:

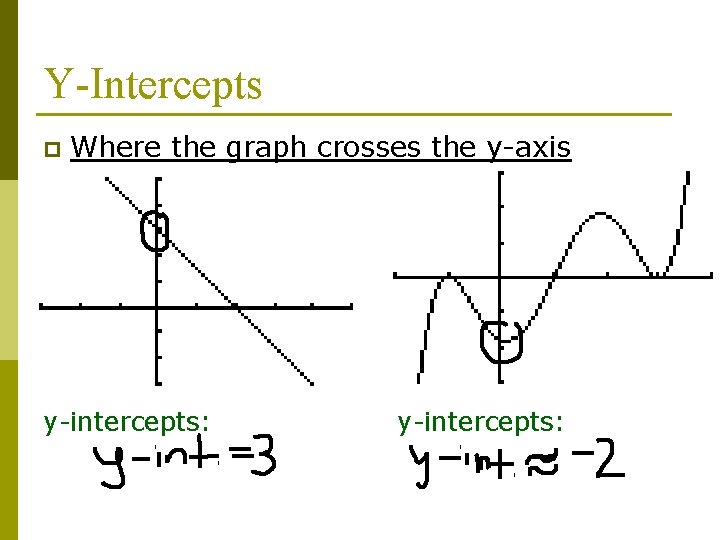
Y-Intercepts p Where the graph crosses the y-axis y-intercepts:

Seek and Solve!!!

Roller Coasters!!! Fujiyama in Japan

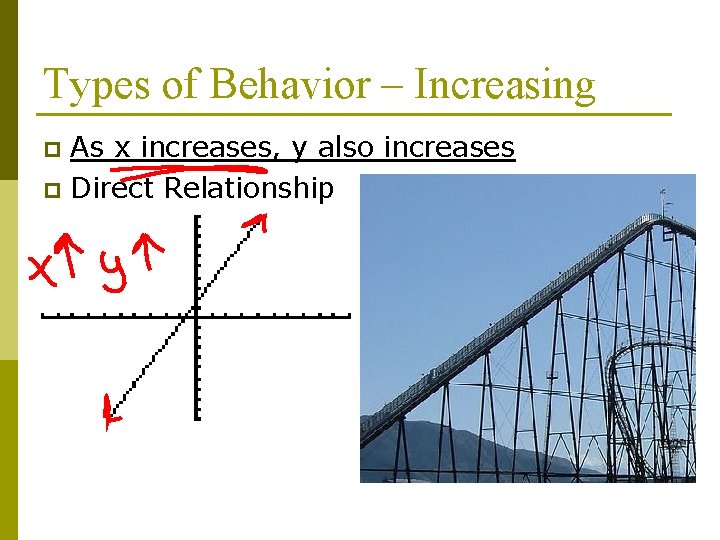
Types of Behavior – Increasing As x increases, y also increases p Direct Relationship p

Types of Behavior – Constant p As x increases, y stays the same

Types of Behavior – Decreasing As x increases, y decreases p Inverse Relationship p

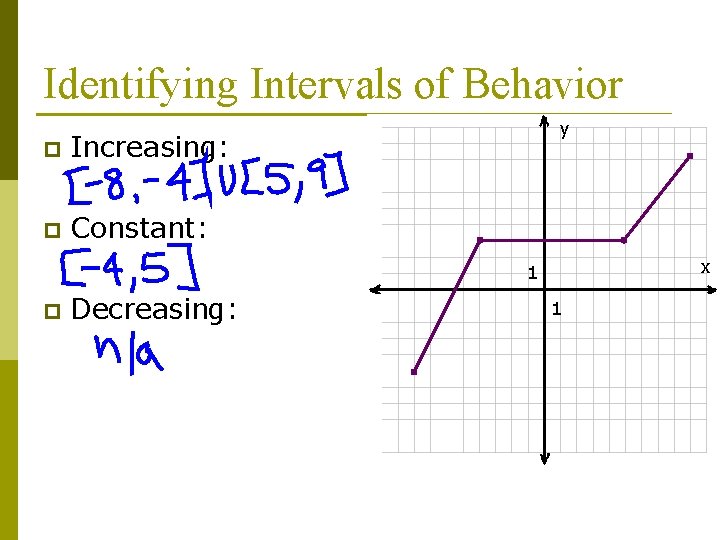
Identifying Intervals of Behavior We use interval notation p The interval measures x-values. The type of behavior describes y-values. Increasing: [0, 4) p The y-values are increasing when the x-values are between 0 inclusive and 4 exclusive

Identifying Intervals of Behavior p Increasing: p Constant: y x 1 p Decreasing: 1

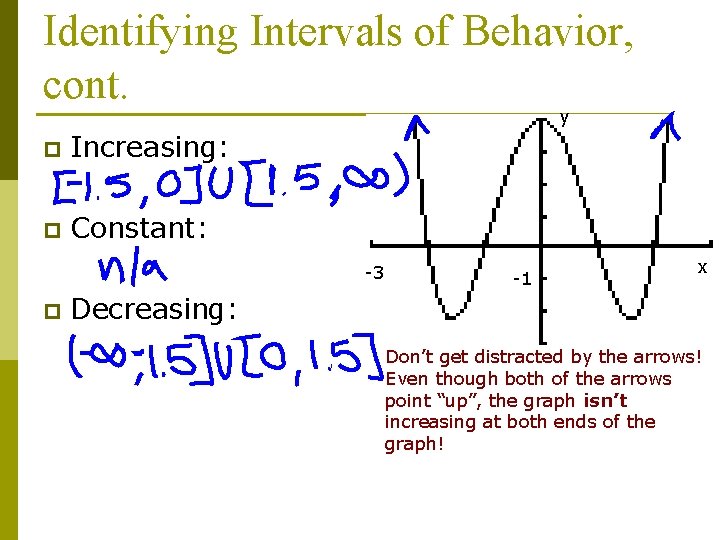
Identifying Intervals of Behavior, cont. y p Increasing: p Constant: -3 p -1 x Decreasing: Don’t get distracted by the arrows! Even though both of the arrows point “up”, the graph isn’t increasing at both ends of the graph!

Your Turn: p Complete problems 1 – 4 on The Key Features of Function Graphs – Part II handout.

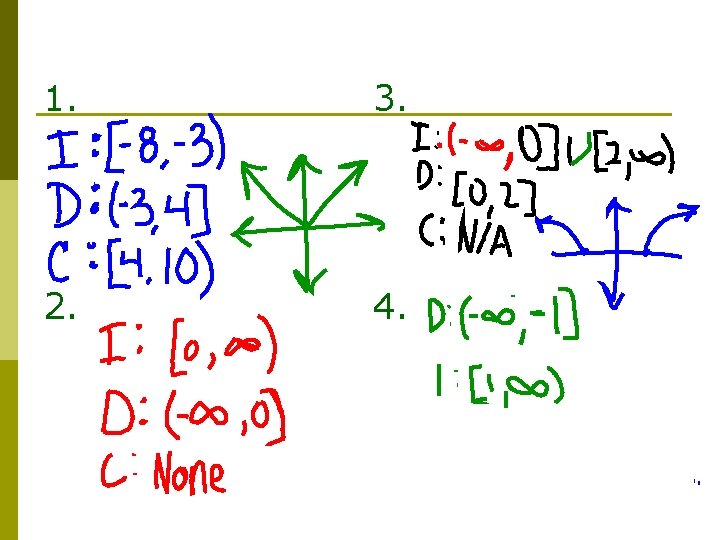
1. 3. 2. 4.

What do you think of when you hear the word parent?

Parent Function The most basic form of a type of function p Determines the general shape of the graph p

Basic Types of Parent Functions 1. 2. 3. 4. Linear Absolute Value Greatest Integer Quadratic 5. 6. 7. 8. Cubic Square Root Cube Root Reciprocal

Function Name: Linear p Parent Function: f(x) = x y p “Baby” Functions: f(x) = 3 x n f(x) = x + 6 n f(x) = – 4 x – 2 2 n 2 x

Your Turn: p Complete problems 5 – 12 on The Key Features of Function Graphs handout