Determine the domain and range of each relation



- Slides: 7

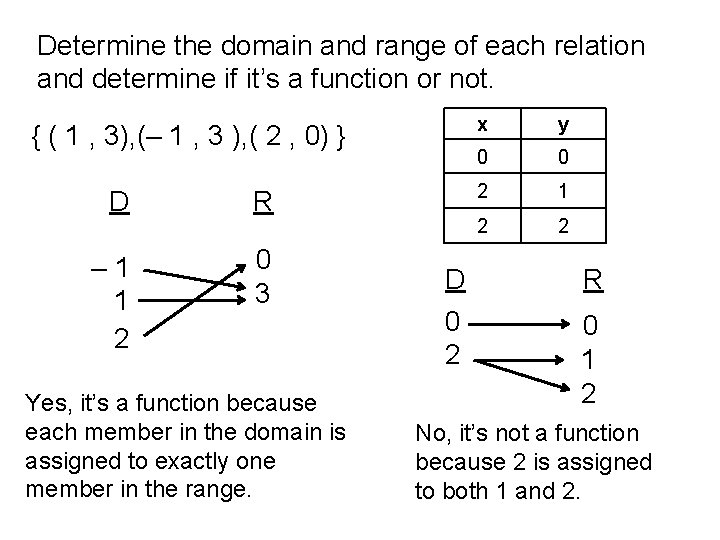
Determine the domain and range of each relation and determine if it’s a function or not. { ( 1 , 3), (– 1 , 3 ), ( 2 , 0) } D R – 1 1 2 0 3 Yes, it’s a function because each member in the domain is assigned to exactly one member in the range. D 0 2 x y 0 0 2 1 2 2 R 0 1 2 No, it’s not a function because 2 is assigned to both 1 and 2.

9. 02 Linear and Non – Linear Functions

Functional Notation The equation y = 5 x + 1 can be rewritten in functional notation. To do this, replace the y with f(x) y = 5 x + 1 f(x) is read as “f of x” Any equation with f(x) is written in functional notation.

We can tell if a function is linear by examination. An equation represents a linear function if all the variables are raised to the first power. Determine if the following represent a linear function. f(x) = x – 4 Yes f(x) = x 2 No, because x is raised to the 2 nd power. f(x) = 2 x + 8 Yes f(x) = 2 Yes f(x) = No, because it’s a square root.

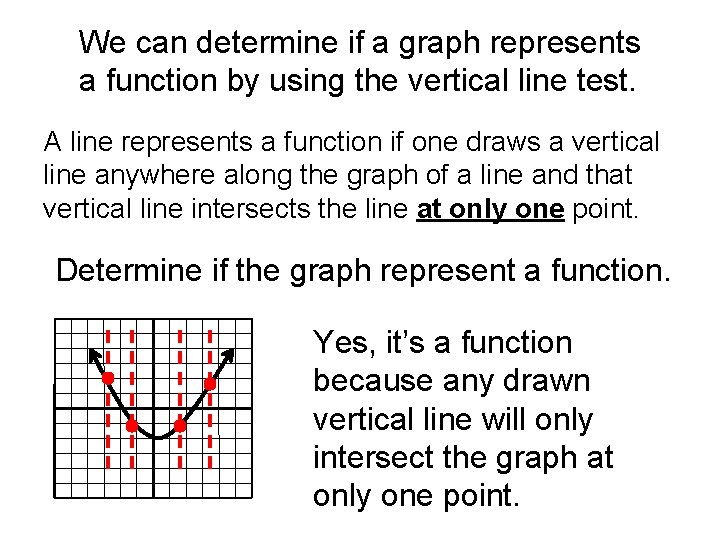
We can determine if a graph represents a function by using the vertical line test. A line represents a function if one draws a vertical line anywhere along the graph of a line and that vertical line intersects the line at only one point. Determine if the graph represent a function. Yes, it’s a function because any drawn vertical line will only intersect the graph at only one point.

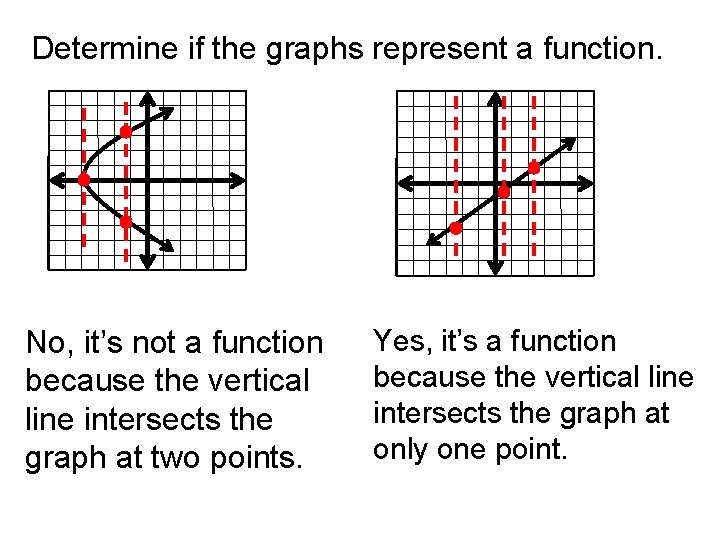
Determine if the graphs represent a function. No, it’s not a function because the vertical line intersects the graph at two points. Yes, it’s a function because the vertical line intersects the graph at only one point.

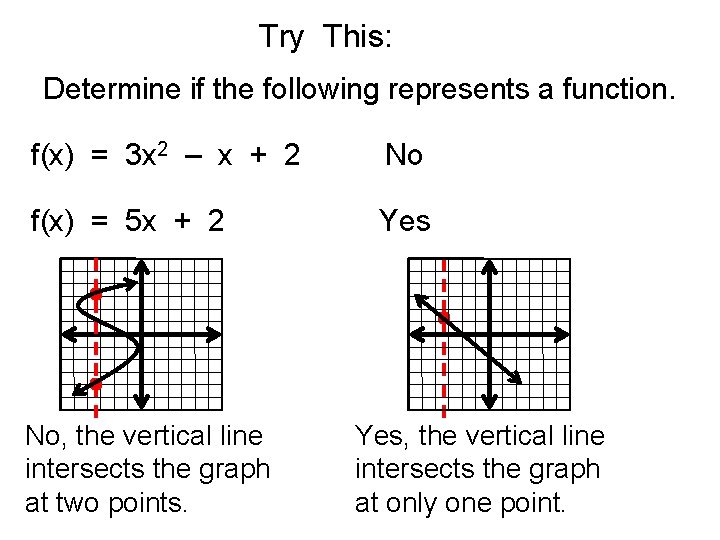
Try This: Determine if the following represents a function. f(x) = 3 x 2 – x + 2 No f(x) = 5 x + 2 Yes No, the vertical line intersects the graph at two points. Yes, the vertical line intersects the graph at only one point.