Determination of the Stokes Radius by measuring the

Determination of the Stokes Radius by measuring the Rotational Diffusion Coefficient: Drot = k. T frot = k. T 8 p Rs 3 Isotropic rotation Dx = Dy = Dz Dx = Dy ≠ Dz Dx ≠Dy ≠ Dz Measure Drot = If you know Rs h microviscosity If you know h Rs molecular size, shape k. T 8 ph. Rs 3

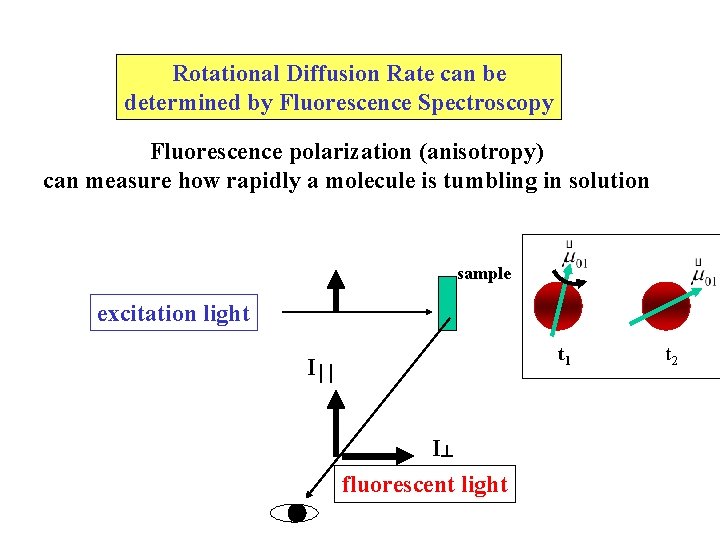
Rotational Diffusion Rate can be determined by Fluorescence Spectroscopy Fluorescence polarization (anisotropy) can measure how rapidly a molecule is tumbling in solution sample excitation light t 1 I I fluorescent light t 2

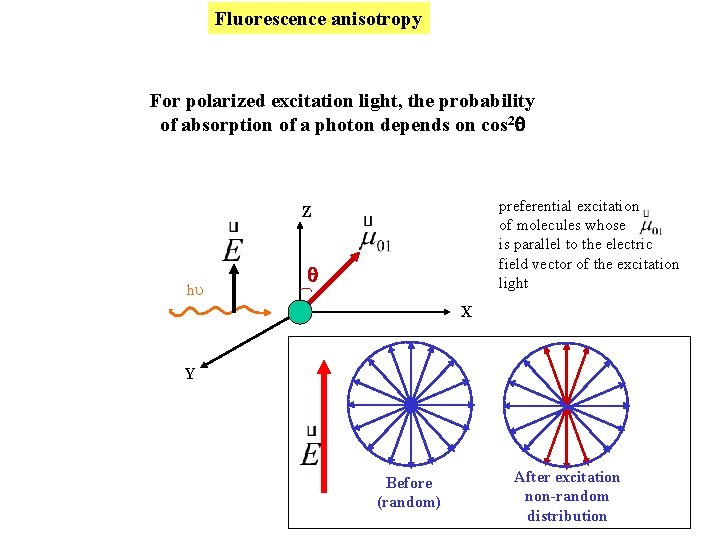
Fluorescence anisotropy For polarized excitation light, the probability of absorption of a photon depends on cos 2 preferential excitation of molecules whose is parallel to the electric field vector of the excitation light Z hu X Y Before (random) After excitation non-random distribution

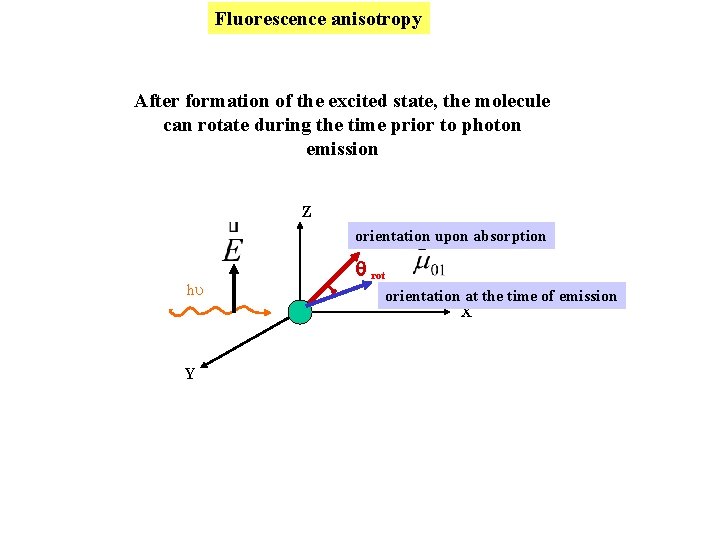
Fluorescence anisotropy After formation of the excited state, the molecule can rotate during the time prior to photon emission Z orientation upon absorption hu Y rot orientation at the time of emission X

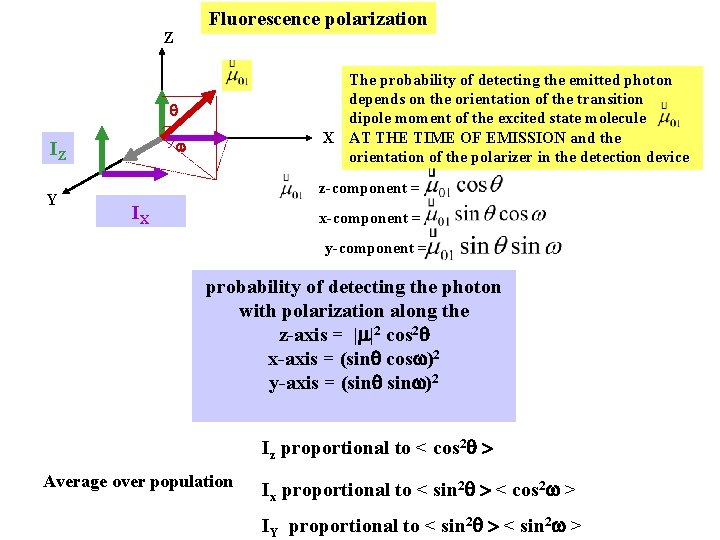
Fluorescence polarization Z The probability of detecting the emitted photon depends on the orientation of the transition dipole moment of the excited state molecule X AT THE TIME OF EMISSION and the orientation of the polarizer in the detection device IZ Y z-component = IX x-component = y-component = probability of detecting the photon with polarization along the z-axis = | |2 cos 2 x-axis = (sin cos )2 y-axis = (sin )2 Iz proportional to < cos 2 > Average over population Ix proportional to < sin 2 > < cos 2 > IY proportional to < sin 2 >

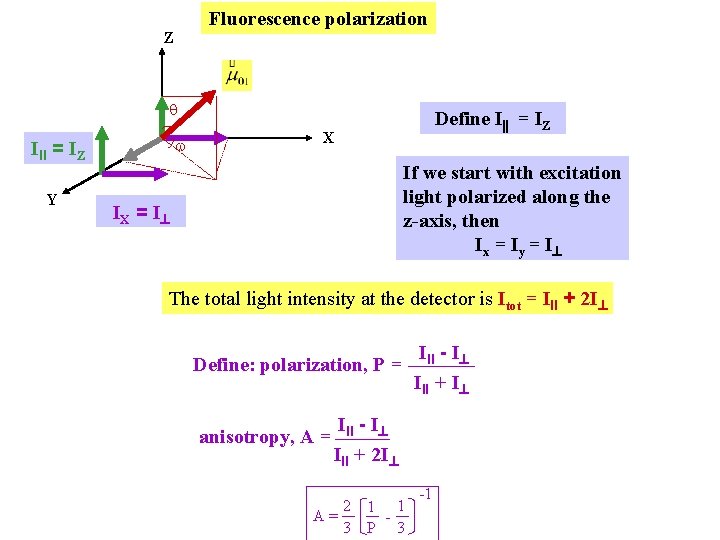
Fluorescence polarization Z q w III = IZ Y Define I = IZ X If we start with excitation light polarized along the z-axis, then Ix = Iy = I IX = I The total light intensity at the detector is Itot = III + 2 I Define: polarization, P = anisotropy, A = III - I III + I III - I III + 2 I 2 1 1 A= 3 P 3 -1

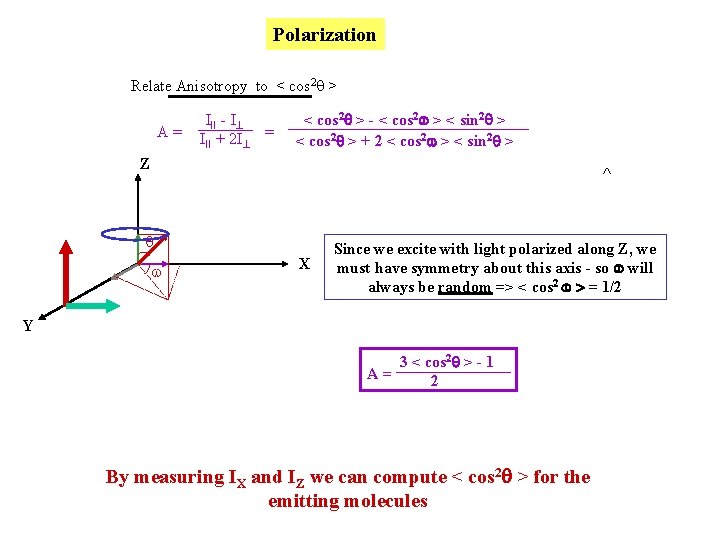
Polarization Relate Anisotropy to < cos 2 q > A= III - I III + 2 I = < cos 2 > - < cos 2 > < sin 2 > < cos 2 > + 2 < cos 2 > < sin 2 > Z ^ q w X Since we excite with light polarized along Z, we must have symmetry about this axis - so will always be random => < cos 2 > = 1/2 Y 3 < cos 2 > - 1 A= 2 By measuring IX and IZ we can compute < cos 2 > for the emitting molecules

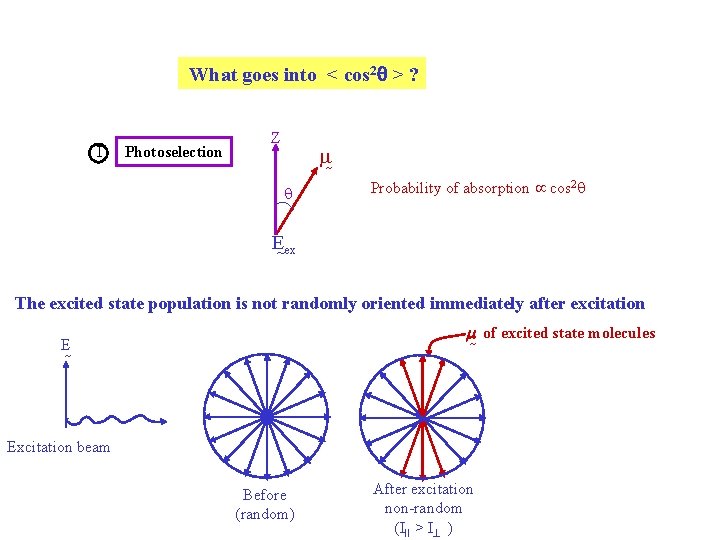
What goes into < cos 2 > ? I Photoselection Z m q Probability of absorption cos 2 q E ex The excited state population is not randomly oriented immediately after excitation m of excited state molecules E Excitation beam Before (random) After excitation non-random (III > I )

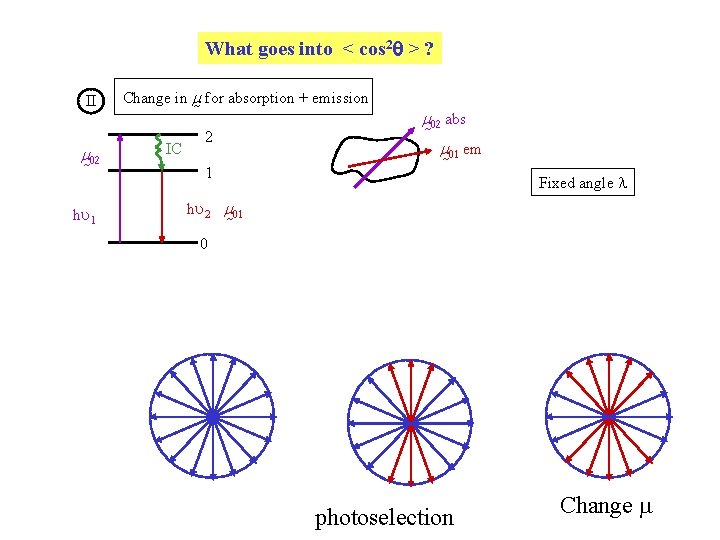
What goes into < cos 2 > ? II m 02 hu 1 Change in m for absorption + emission IC 2 m 02 abs m 01 em 1 Fixed angle l hu 2 m 01 0 photoselection Change m

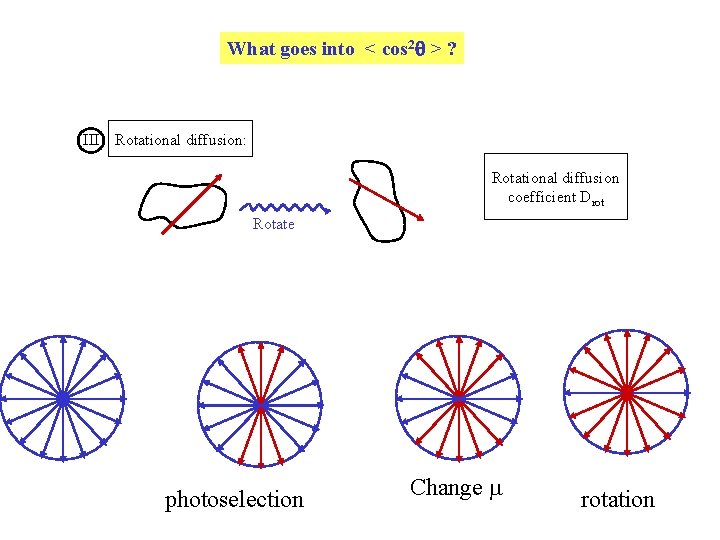
What goes into < cos 2 > ? III Rotational diffusion: Rotational diffusion coefficient Drot Rotate photoselection Change m rotation

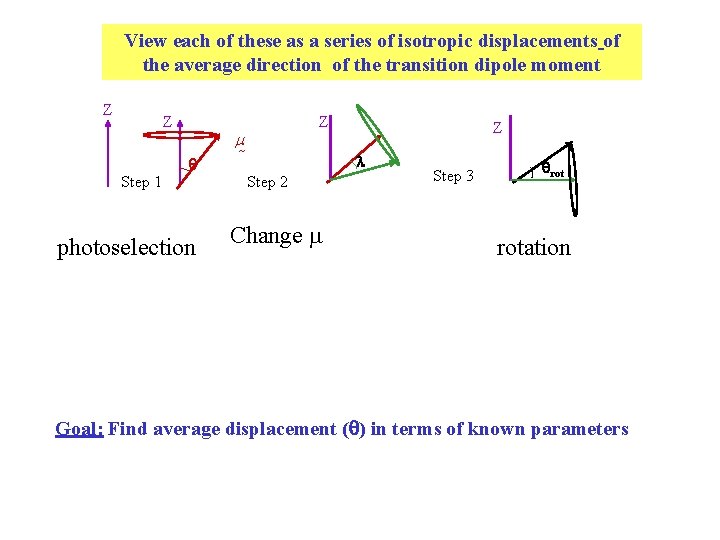
View each of these as a series of isotropic displacements of the average direction of the transition dipole moment Z Z Step 1 photoselection Z m Z l Step 2 Change m Step 3 rotation Goal: Find average displacement ( ) in terms of known parameters

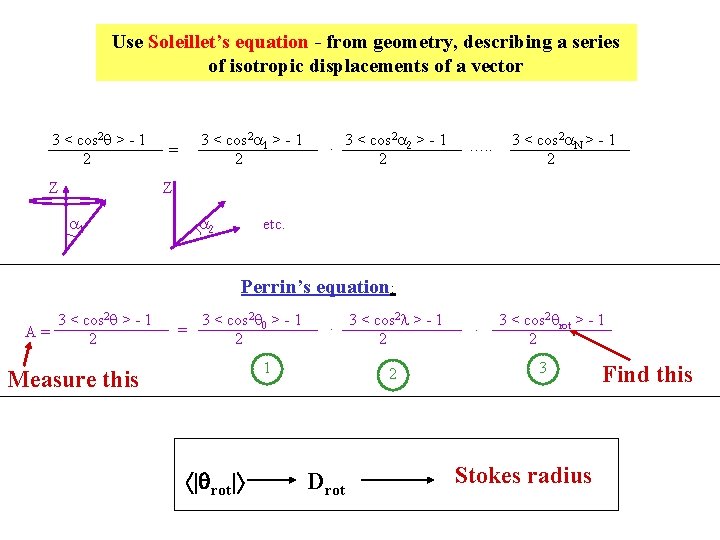
Use Soleillet’s equation - from geometry, describing a series of isotropic displacements of a vector 3 < cos 2 q > - 1 2 Z 3 < cos 2 a 1 > - 1 2 = 2. 3 < cos a 2 > - 1 2 …. . 3 < cos 2 a. N > - 1 2 Z a 1 a 2 etc. Perrin’s equation: 3 < cos 2 q > - 1 A= 2 = 3 < cos 2 q 0 > - 1 2 2. 3 < cos l > - 1 2 1 Measure this | rot| 2 Drot . 3 < cos 2 qrot > - 1 2 3 Stokes radius Find this

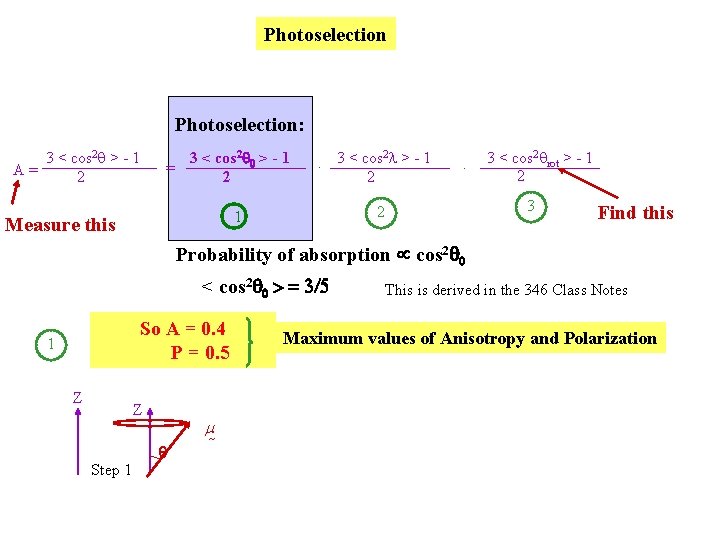
Photoselection: 3 < cos 2 q > - 1 A= 2 3 < cos 2 0 > - 1 = 2 2. 3 < cos l > - 1 2 3 < cos 2 qrot > - 1 2 3 2 1 Measure this . Find this Probability of absorption cos 2 0 < cos 2 0 > = 3/5 So A = 0. 4 P = 0. 5 1 Z Z Step 1 m This is derived in the 346 Class Notes Maximum values of Anisotropy and Polarization

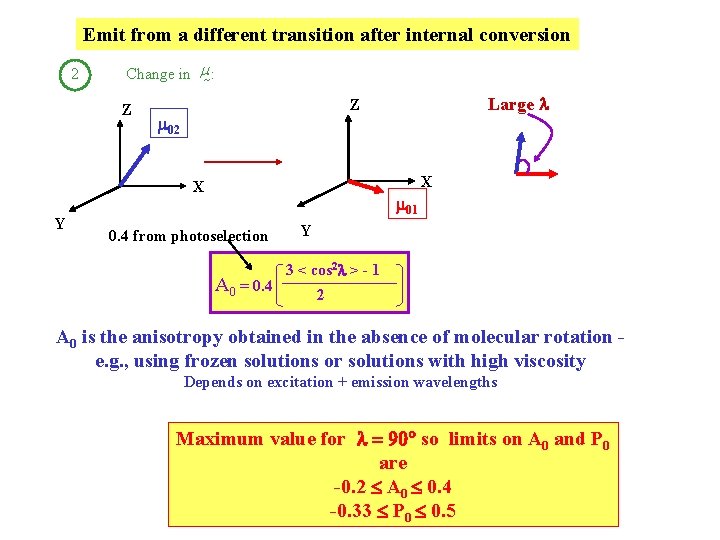
Emit from a different transition after internal conversion 2 Change in m : Z 02 X X Y Large l Z 01 0. 4 from photoselection A 0 = 0. 4 Y 3 < cos 2 l > - 1 2 A 0 is the anisotropy obtained in the absence of molecular rotation e. g. , using frozen solutions or solutions with high viscosity Depends on excitation + emission wavelengths Maximum value for l = 90 so limits on A 0 and P 0 are -0. 2 A 0 0. 4 -0. 33 P 0 0. 5

Rotational Diffusion: will always tend to bring A 0 or P 0 A = A 0 3 < cos 2 rot > - 1 2 Anisotropy of frozen sample < cos 2 rot > = 1 if there is no rotation: A = Ao < cos 2 rot > =1/3 for random orientation: A = 0 rot

Rotational Diffusion 3 Rotational Diffusion: will always tend to bring A 0 or P 0 Ao value from photoselection plus change in 3 < cos 2 rot > - 1 A = A 0 2 Break down rotation into a series of N isotropic steps of size d 3 < cos 2 q > - 1 2 Z = 3 < cos 2 d > - 1 2 2. 3 < cos d > - 1 2 …. . 3 < cos 2 d > - 1 2 Z d d etc. cos 2 d = 1 - sin 2 d 1 - d 2 For a small “step” Rotational Diffusion: < d 2 > = 4 Drot dt = 1 - 4 Drot dt N 3 < cos 2 rot > - 1 = (1 - 6 Drot dt)t/dt 2

Rotational Diffusion N 3 < cos 2 rot > - 1 = (1 - 6 Drot dt)t/dt 2 But (1 -x) e-x for x << 1 3 < cos 2 rot > - 1 = e- 6 Drott 2 A = A 0 e- 6 Drot t Time-resolved Anisotropy yields Drot Monitor anisotropy following a pulse of excitation light: Calculate Drot A time

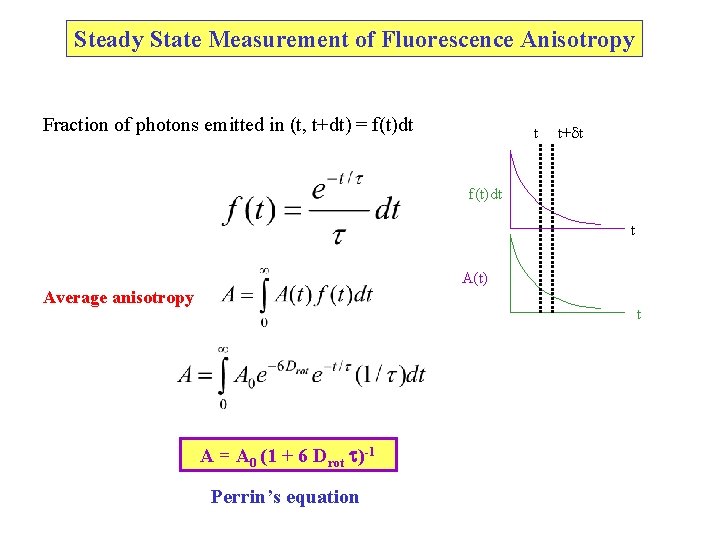
Steady State Measurement of Fluorescence Anisotropy Fraction of photons emitted in (t, t+dt) = f(t)dt t t+ t f(t)dt t A(t) Average anisotropy t A = A 0 (1 + 6 Drot t)-1 Perrin’s equation

Various forms of Perrin’s equation (1) (2) V molecular volume substitute : (3) (4) Perrin plot 1 - 1 P 3 Define: rotational diffusion time = T (5)

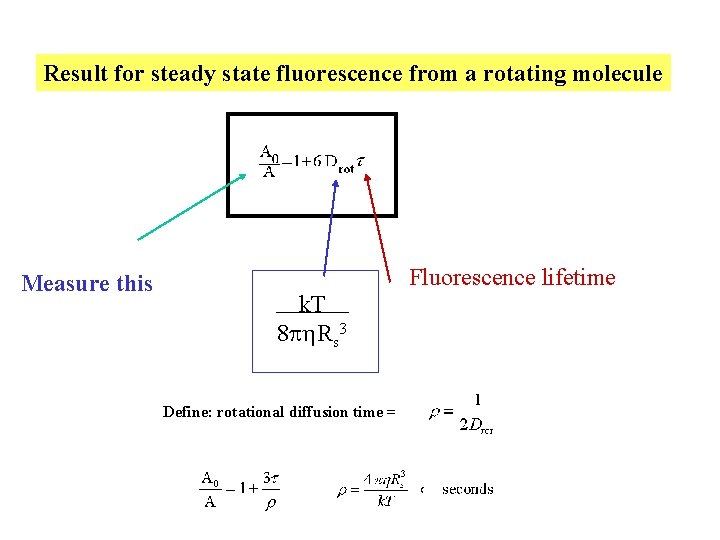
Result for steady state fluorescence from a rotating molecule Measure this Fluorescence lifetime k. T 8 p Rs 3 Define: rotational diffusion time =

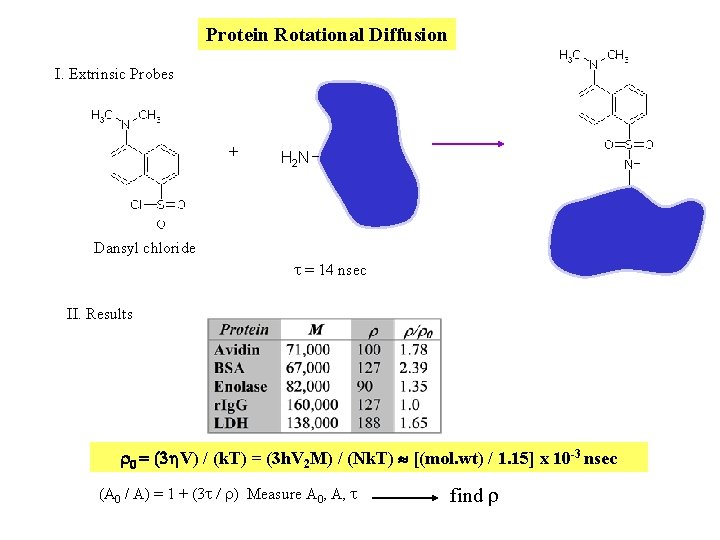
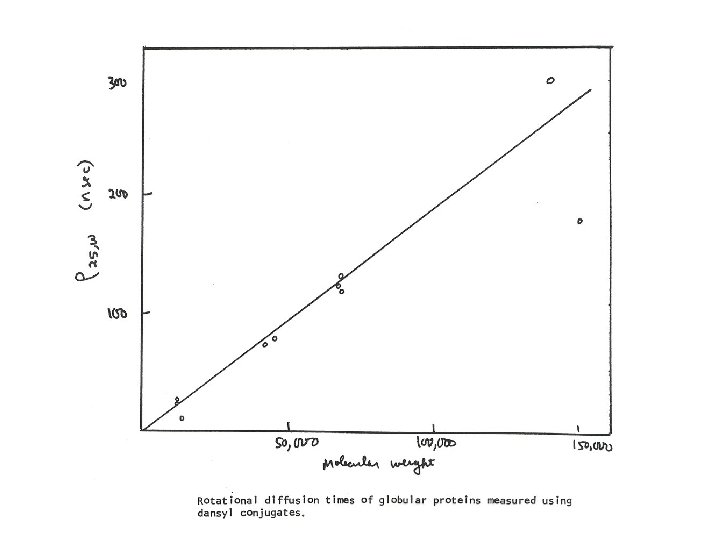
Protein Rotational Diffusion I. Extrinsic Probes + H 2 N Dansyl chloride t = 14 nsec II. Results r 0 = (3 h. V) / (k. T) = (3 h. V 2 M) / (Nk. T) [(mol. wt) / 1. 15] x 10 -3 nsec (A 0 / A) = 1 + (3 t / r) Measure A 0, A, t find r

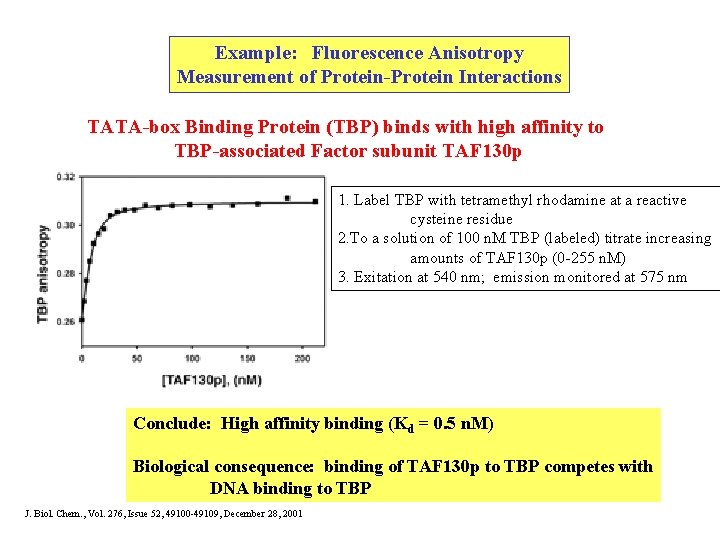
Example: Fluorescence Anisotropy Measurement of Protein-Protein Interactions TATA-box Binding Protein (TBP) binds with high affinity to TBP-associated Factor subunit TAF 130 p 1. Label TBP with tetramethyl rhodamine at a reactive cysteine residue 2. To a solution of 100 n. M TBP (labeled) titrate increasing amounts of TAF 130 p (0 -255 n. M) 3. Exitation at 540 nm; emission monitored at 575 nm Conclude: High affinity binding (Kd = 0. 5 n. M) Biological consequence: binding of TAF 130 p to TBP competes with DNA binding to TBP J. Biol. Chem. , Vol. 276, Issue 52, 49100 -49109, December 28, 2001

Fluorescence Anisotropy used to monitor Protein-DNA Interactions 1. 50 n. M Rhodamine labeled DNA 2. Titrate TBP 3. Excitation at 580 nm/Emission at 630 nm SHOWS 1: 1 COMPLEX 1. 1: 1 DNA: TBP complex, with labeled DNA (50, 100, 250 nm TBP) 2. Titrate TAF 130 p SHOWS ELIMINATION OF TBP-DNA COMPLEX BY COMPETING TAF 130 p 1. 50 nm labeled DNA 2. Titrate with TAF 130 p SHOWS NO COMPLEX BETWEEN DNA AND TAF 130 p J. Biol. Chem. , Vol. 276, Issue 52, 49100 -49109, December 28, 2001

Fluorescence anisotropy used to measure microviscosity The rotational diffusion coefficient can be related to Molecular volume: V V molecular volume Measure this If you know V You can determine

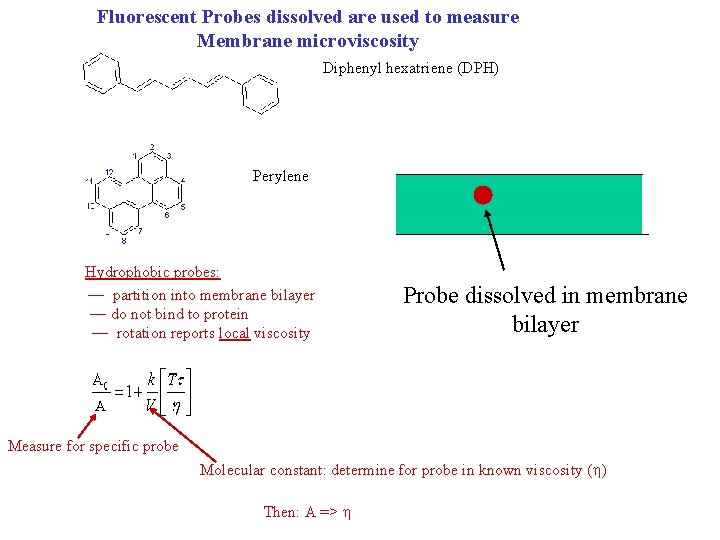
Fluorescent Probes dissolved are used to measure Membrane microviscosity Diphenyl hexatriene (DPH) Perylene Hydrophobic probes: — partition into membrane bilayer — do not bind to protein — rotation reports local viscosity Probe dissolved in membrane bilayer Measure for specific probe Molecular constant: determine for probe in known viscosity ( ) Then: A =>

Typically: for biological membranes 1 Poise 100 -times the viscosity of water Note: (1 / ) = fluidity of membrane

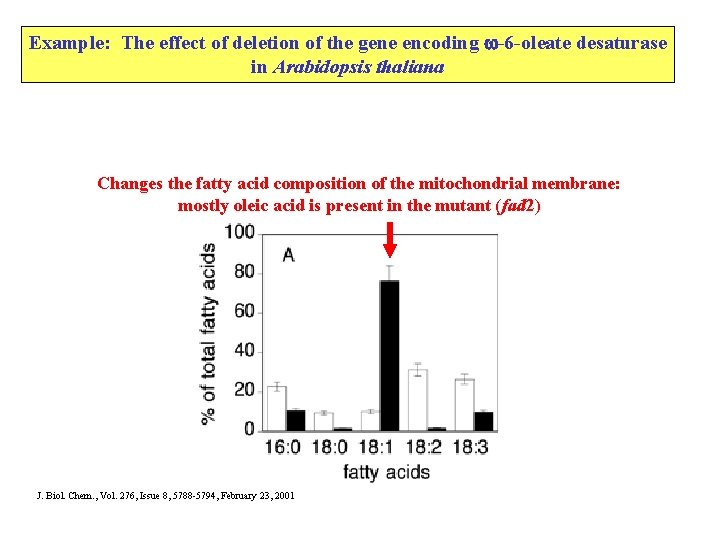
Example: The effect of deletion of the gene encoding -6 -oleate desaturase in Arabidopsis thaliana Changes the fatty acid composition of the mitochondrial membrane: mostly oleic acid is present in the mutant (fad 2) J. Biol. Chem. , Vol. 276, Issue 8, 5788 -5794, February 23, 2001

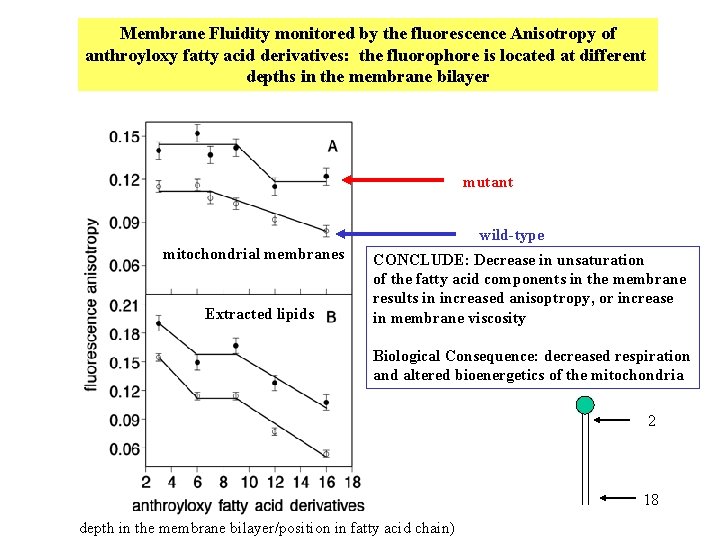
Membrane Fluidity monitored by the fluorescence Anisotropy of anthroyloxy fatty acid derivatives: the fluorophore is located at different depths in the membrane bilayer mutant wild-type mitochondrial membranes Extracted lipids CONCLUDE: Decrease in unsaturation of the fatty acid components in the membrane results in increased anisoptropy, or increase in membrane viscosity Biological Consequence: decreased respiration and altered bioenergetics of the mitochondria 2 18 depth in the membrane bilayer/position in fatty acid chain)