Determination of the Stokes Radius by measuring the

Determination of the Stokes Radius by measuring the Rotational Diffusion Coefficient: Drot = k. T frot = k. T 8 p Rs 3 Isotropic rotation Dx = Dy = Dz Dx = Dy ≠ Dz Dx ≠Dy ≠ Dz Measure Drot = If you know Rs h microviscosity If you know h Rs molecular size, shape k. T 8 ph. Rs 3

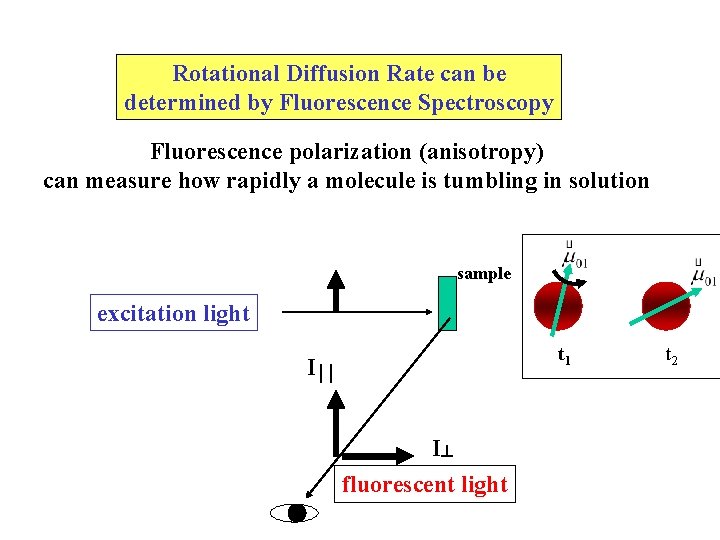
Rotational Diffusion Rate can be determined by Fluorescence Spectroscopy Fluorescence polarization (anisotropy) can measure how rapidly a molecule is tumbling in solution sample excitation light t 1 I I fluorescent light t 2

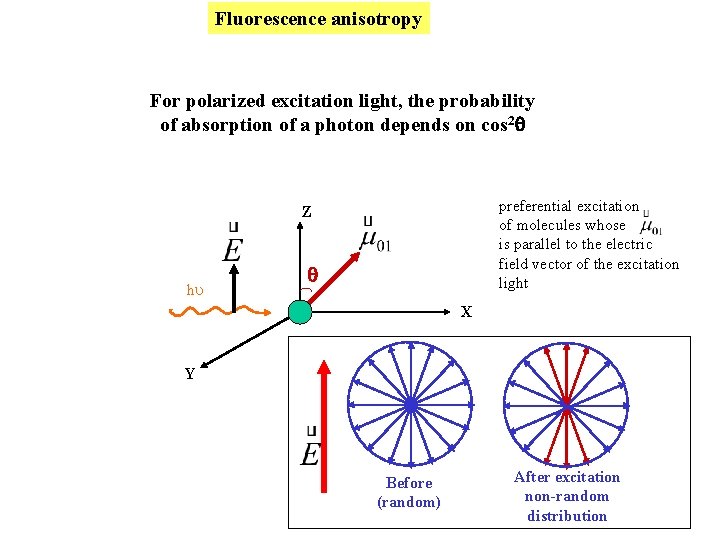
Fluorescence anisotropy For polarized excitation light, the probability of absorption of a photon depends on cos 2 preferential excitation of molecules whose is parallel to the electric field vector of the excitation light Z hu X Y Before (random) After excitation non-random distribution

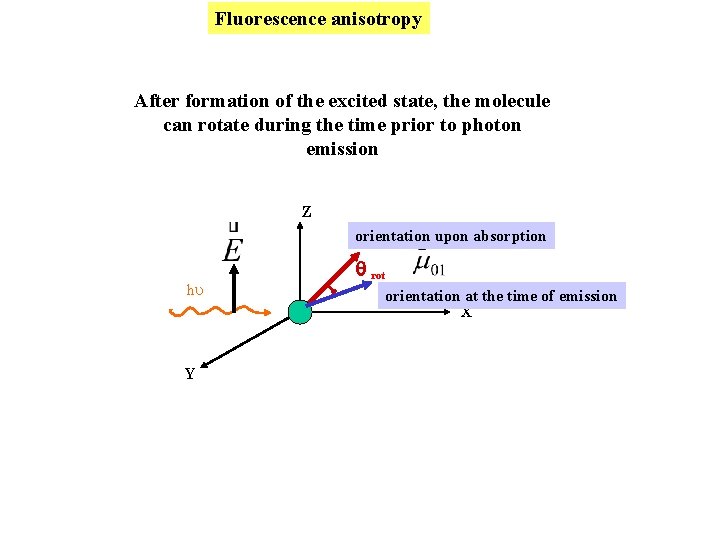
Fluorescence anisotropy After formation of the excited state, the molecule can rotate during the time prior to photon emission Z orientation upon absorption hu Y rot orientation at the time of emission X

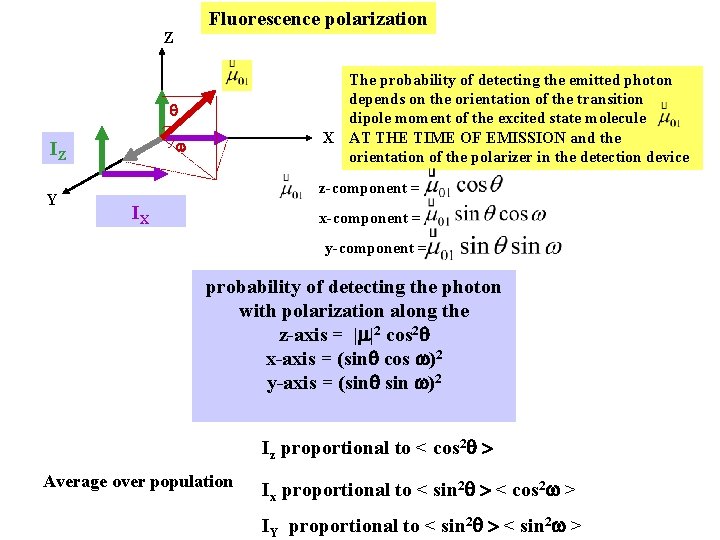
Fluorescence polarization Z The probability of detecting the emitted photon depends on the orientation of the transition dipole moment of the excited state molecule X AT THE TIME OF EMISSION and the orientation of the polarizer in the detection device IZ Y z-component = IX x-component = y-component = probability of detecting the photon with polarization along the z-axis = | |2 cos 2 x-axis = (sin cos )2 y-axis = (sin )2 Iz proportional to < cos 2 > Average over population Ix proportional to < sin 2 > < cos 2 > IY proportional to < sin 2 >

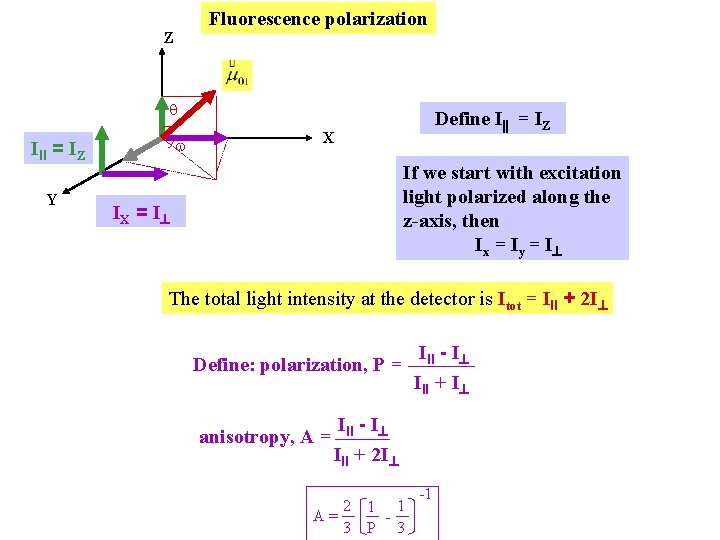
Fluorescence polarization Z q w III = IZ Y Define I = IZ X If we start with excitation light polarized along the z-axis, then Ix = Iy = I IX = I The total light intensity at the detector is Itot = III + 2 I Define: polarization, P = anisotropy, A = III - I III + I III - I III + 2 I 2 1 1 A= 3 P 3 -1

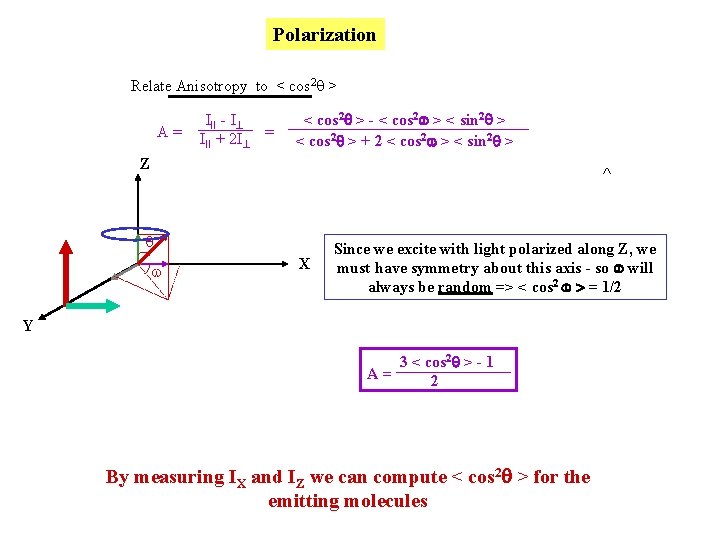
Polarization Relate Anisotropy to < cos 2 q > A= III - I III + 2 I = < cos 2 > - < cos 2 > < sin 2 > < cos 2 > + 2 < cos 2 > < sin 2 > Z ^ q w X Since we excite with light polarized along Z, we must have symmetry about this axis - so will always be random => < cos 2 > = 1/2 Y 3 < cos 2 > - 1 A= 2 By measuring IX and IZ we can compute < cos 2 > for the emitting molecules

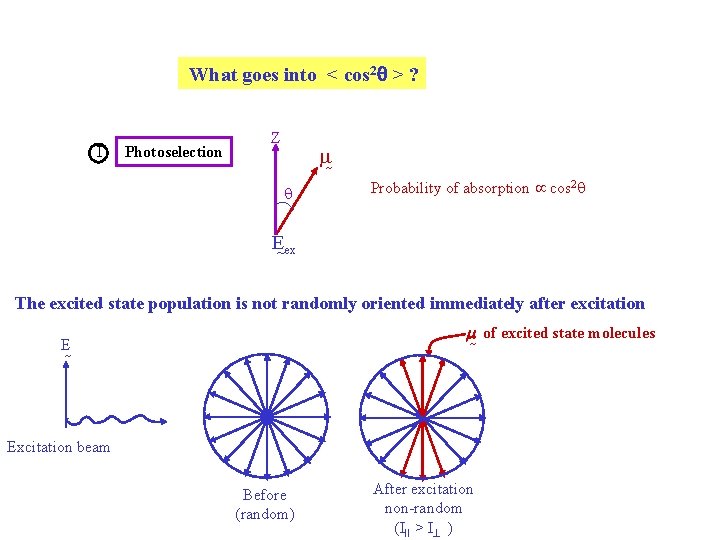
What goes into < cos 2 > ? I Photoselection Z q Probability of absorption cos 2 q E ex The excited state population is not randomly oriented immediately after excitation m of excited state molecules E Excitation beam Before (random) After excitation non-random (III > I )

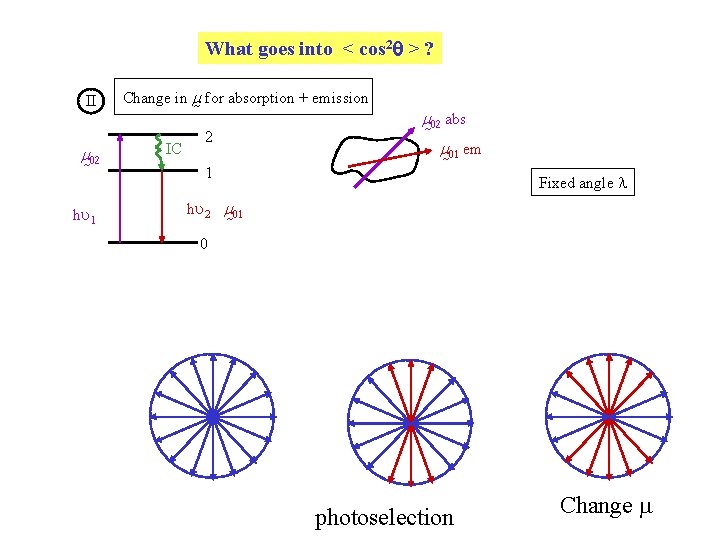
What goes into < cos 2 > ? II m 02 hu 1 Change in m for absorption + emission IC 2 m 02 abs m 01 em 1 Fixed angle l hu 2 m 01 0 photoselection Change

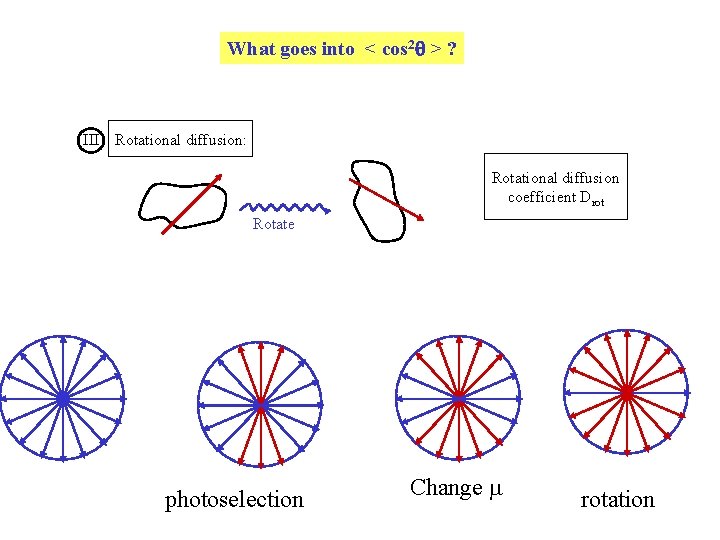
What goes into < cos 2 > ? III Rotational diffusion: Rotational diffusion coefficient Drot Rotate photoselection Change rotation

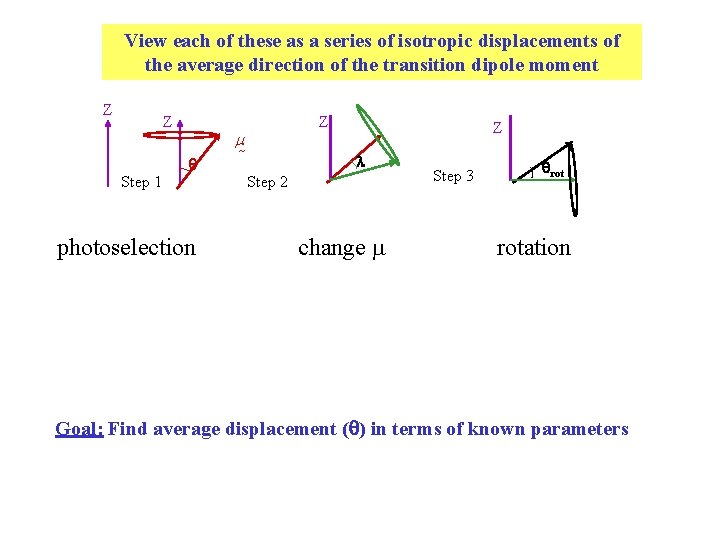
View each of these as a series of isotropic displacements of the average direction of the transition dipole moment Z Z Step 1 photoselection Z m Z l Step 2 change Step 3 rotation Goal: Find average displacement ( ) in terms of known parameters

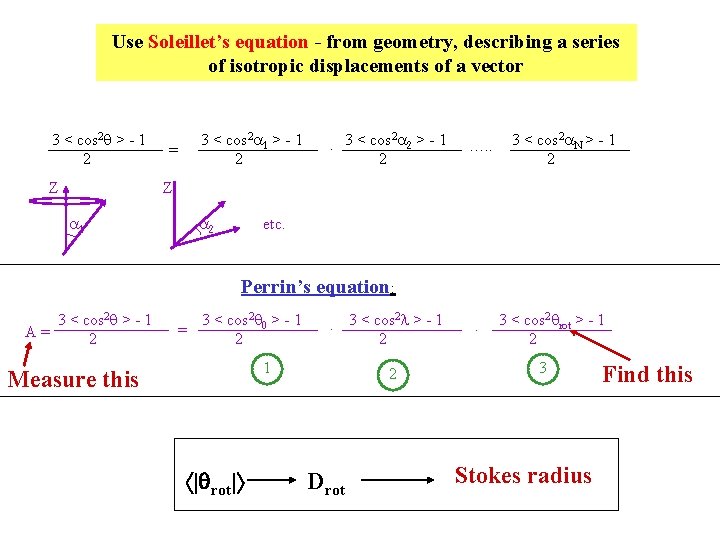
Use Soleillet’s equation - from geometry, describing a series of isotropic displacements of a vector 3 < cos 2 q > - 1 2 Z 3 < cos 2 a 1 > - 1 2 = 2. 3 < cos a 2 > - 1 2 …. . 3 < cos 2 a. N > - 1 2 Z a 1 a 2 etc. Perrin’s equation: 3 < cos 2 q > - 1 A= 2 = 3 < cos 2 q 0 > - 1 2 2. 3 < cos l > - 1 2 1 Measure this | rot| 2 Drot . 3 < cos 2 qrot > - 1 2 3 Stokes radius Find this

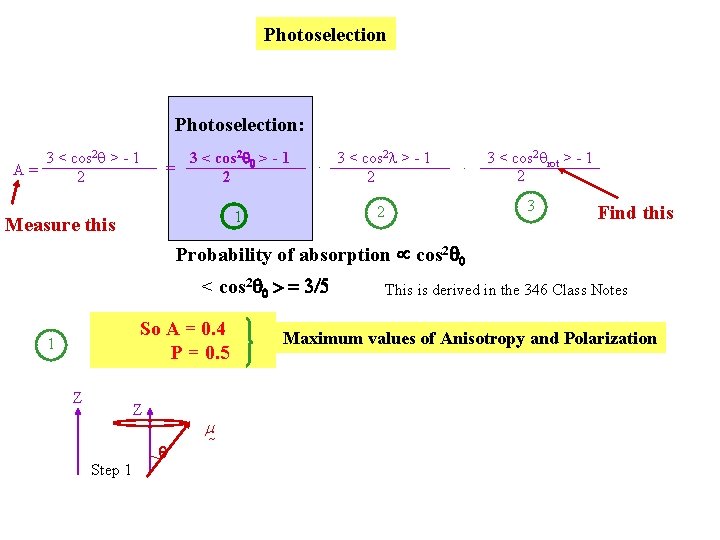
Photoselection: 3 < cos 2 q > - 1 A= 2 3 < cos 2 0 > - 1 = 2 2. 3 < cos l > - 1 2 3 < cos 2 qrot > - 1 2 3 2 1 Measure this . Find this Probability of absorption cos 2 0 < cos 2 0 > = 3/5 So A = 0. 4 P = 0. 5 1 Z Z Step 1 m This is derived in the 346 Class Notes Maximum values of Anisotropy and Polarization

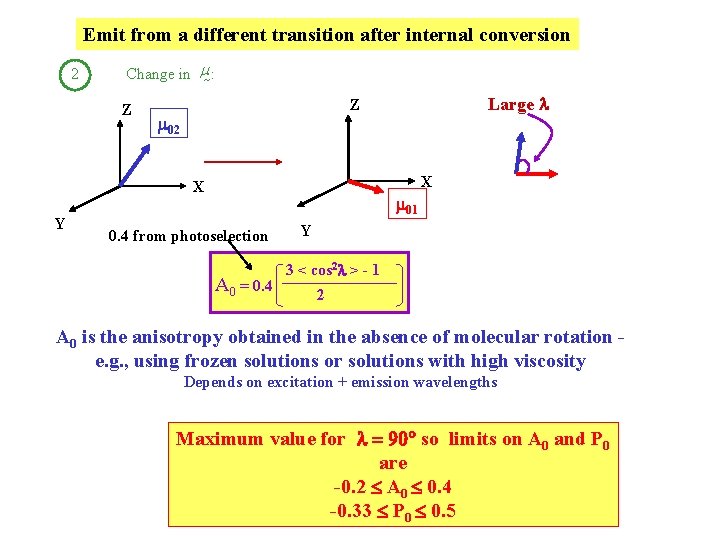
Emit from a different transition after internal conversion 2 Change in m : Z 02 X X Y Large l Z 01 0. 4 from photoselection A 0 = 0. 4 Y 3 < cos 2 l > - 1 2 A 0 is the anisotropy obtained in the absence of molecular rotation e. g. , using frozen solutions or solutions with high viscosity Depends on excitation + emission wavelengths Maximum value for l = 90 so limits on A 0 and P 0 are -0. 2 A 0 0. 4 -0. 33 P 0 0. 5

Rotational Diffusion: will always tend to bring A 0 or P 0 A = A 0 3 < cos 2 rot > - 1 2 Anisotropy of frozen sample < cos 2 rot > = 1 if there is no rotation: A = Ao < cos 2 rot > =1/3 for random orientation: A = 0 rot

Rotational Diffusion 3 Rotational Diffusion: will always tend to bring A 0 or P 0 Ao value from photoselection plus change in 3 < cos 2 rot > - 1 A = A 0 2 Break down rotation into a series of N isotropic steps of size d 3 < cos 2 q > - 1 2 Z = 3 < cos 2 d > - 1 2 2. 3 < cos d > - 1 2 …. . 3 < cos 2 d > - 1 2 Z d d etc. cos 2 d = 1 - sin 2 d 1 - d 2 For a small “step” Rotational Diffusion: < d 2 > = 4 Drot dt = 1 - 4 Drot dt N 3 < cos 2 rot > - 1 = (1 - 6 Drot dt)t/dt 2

Rotational Diffusion N 3 < cos 2 rot > - 1 = (1 - 6 Drot dt)t/dt 2 But (1 -x) e-x for x << 1 3 < cos 2 rot > - 1 = e- 6 Drott 2 A = A 0 e- 6 Drot t Time-resolved Anisotropy yields Drot Monitor anisotropy following a pulse of excitation light: Calculate Drot A time

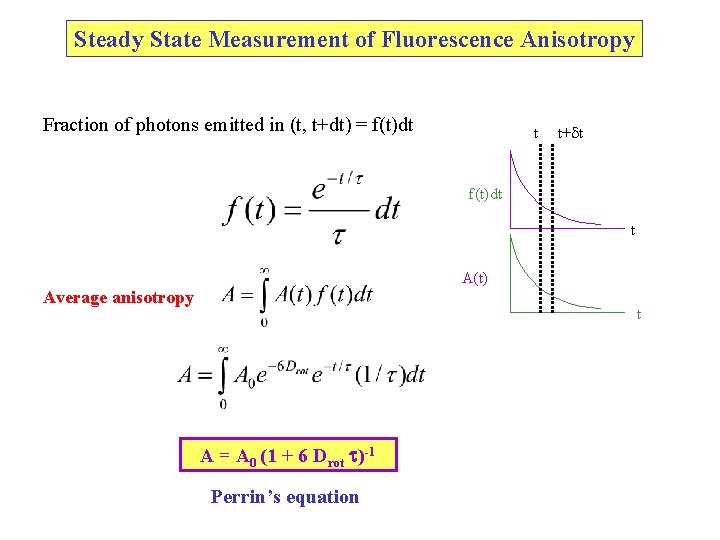
Steady State Measurement of Fluorescence Anisotropy Fraction of photons emitted in (t, t+dt) = f(t)dt t t+ t f(t)dt t A(t) Average anisotropy t A = A 0 (1 + 6 Drot t)-1 Perrin’s equation

Various forms of Perrin’s equation (1) (2) V molecular volume substitute : (3) (4) Perrin plot 1 - 1 P 3 Define: rotational diffusion time = T (5)

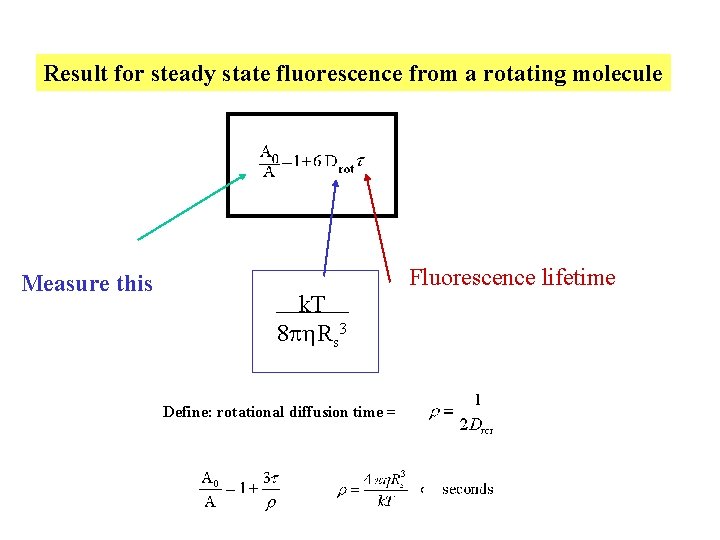
Result for steady state fluorescence from a rotating molecule Measure this Fluorescence lifetime k. T 8 p Rs 3 Define: rotational diffusion time =

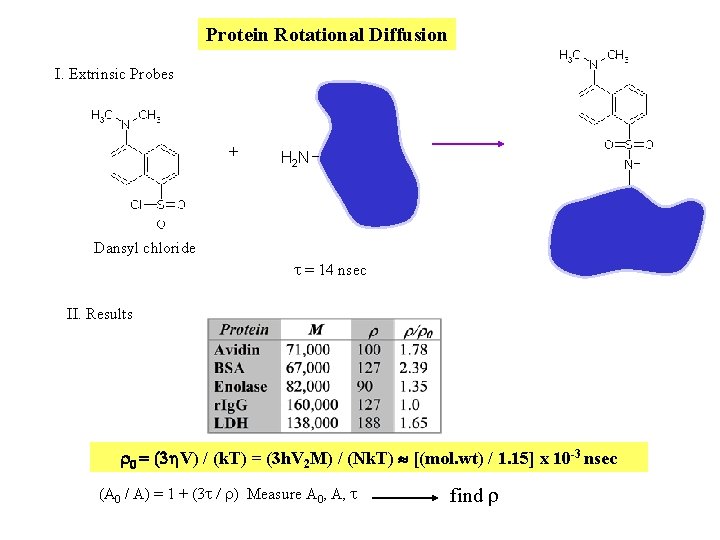
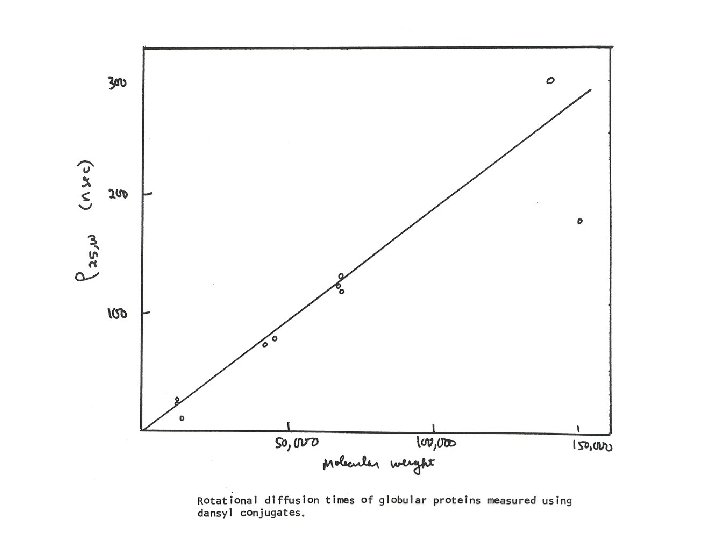
Protein Rotational Diffusion I. Extrinsic Probes + H 2 N Dansyl chloride t = 14 nsec II. Results r 0 = (3 h. V) / (k. T) = (3 h. V 2 M) / (Nk. T) [(mol. wt) / 1. 15] x 10 -3 nsec (A 0 / A) = 1 + (3 t / r) Measure A 0, A, t find r

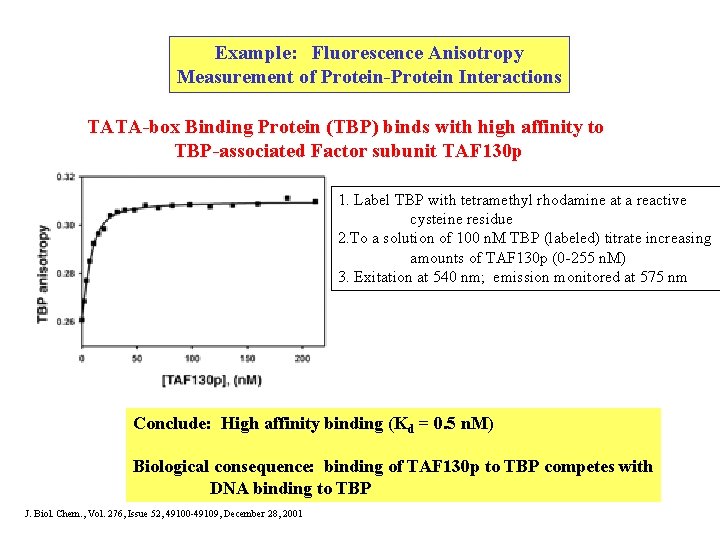
Example: Fluorescence Anisotropy Measurement of Protein-Protein Interactions TATA-box Binding Protein (TBP) binds with high affinity to TBP-associated Factor subunit TAF 130 p 1. Label TBP with tetramethyl rhodamine at a reactive cysteine residue 2. To a solution of 100 n. M TBP (labeled) titrate increasing amounts of TAF 130 p (0 -255 n. M) 3. Exitation at 540 nm; emission monitored at 575 nm Conclude: High affinity binding (Kd = 0. 5 n. M) Biological consequence: binding of TAF 130 p to TBP competes with DNA binding to TBP J. Biol. Chem. , Vol. 276, Issue 52, 49100 -49109, December 28, 2001

Fluorescence Anisotropy used to monitor Protein-DNA Interactions 1. 50 n. M Rhodamine labeled DNA 2. Titrate TBP 3. Excitation at 580 nm/Emission at 630 nm SHOWS 1: 1 COMPLEX 1. 1: 1 DNA: TBP complex, with labeled DNA (50, 100, 250 nm TBP) 2. Titrate TAF 130 p SHOWS ELIMINATION OF TBP-DNA COMPLEX BY COMPETING TAF 130 p 1. 50 nm labeled DNA 2. Titrate with TAF 130 p SHOWS NO COMPLEX BETWEEN DNA AND TAF 130 p J. Biol. Chem. , Vol. 276, Issue 52, 49100 -49109, December 28, 2001

Fluorescence anisotropy used to measure microviscosity The rotational diffusion coefficient can be related to Molecular volume: V V molecular volume Measure this If you know V You can determine

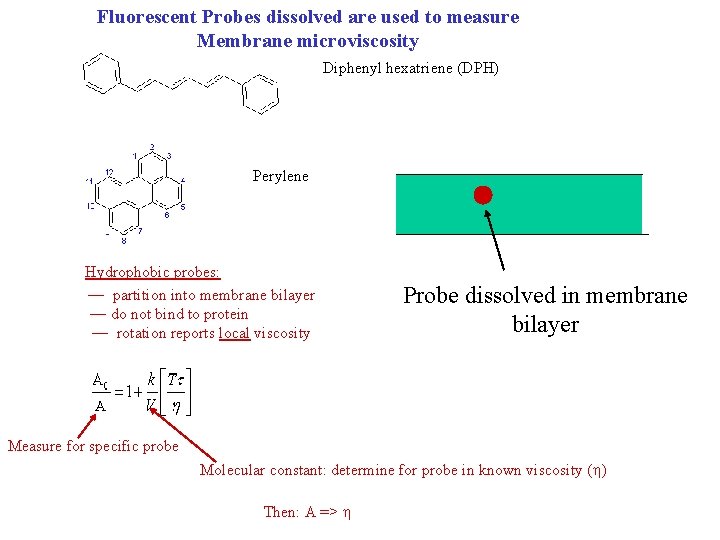
Fluorescent Probes dissolved are used to measure Membrane microviscosity Diphenyl hexatriene (DPH) Perylene Hydrophobic probes: — partition into membrane bilayer — do not bind to protein — rotation reports local viscosity Probe dissolved in membrane bilayer Measure for specific probe Molecular constant: determine for probe in known viscosity ( ) Then: A =>

Typically: for biological membranes 1 Poise 100 -times the viscosity of water Note: (1 / ) = fluidity of membrane

Typically: for biological membranes, h 1 Poise (~100 X water viscosity) Note: (1 / h) = fluidity of membrane Two points: (1) Do not know where probe is located in the bilayer - maybe regions of differing fluidity. Where is probe? (2) Probes are not spherical. Hence, the specific model of how it moves will influence final interpretation

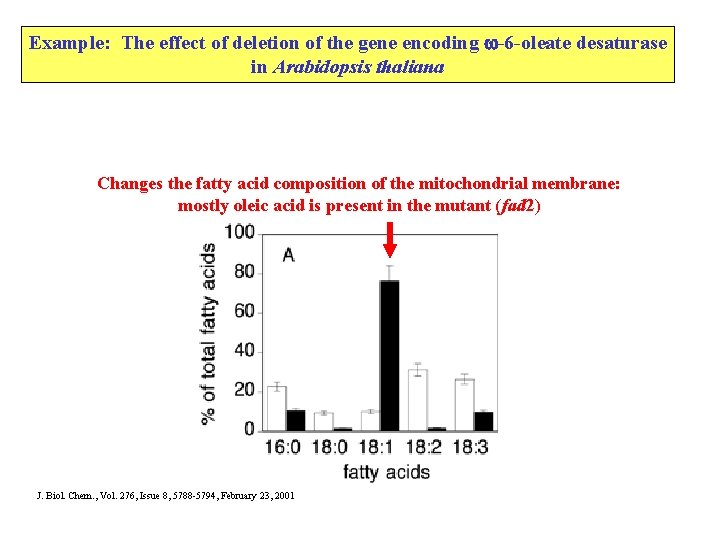
Example: The effect of deletion of the gene encoding -6 -oleate desaturase in Arabidopsis thaliana Changes the fatty acid composition of the mitochondrial membrane: mostly oleic acid is present in the mutant (fad 2) J. Biol. Chem. , Vol. 276, Issue 8, 5788 -5794, February 23, 2001

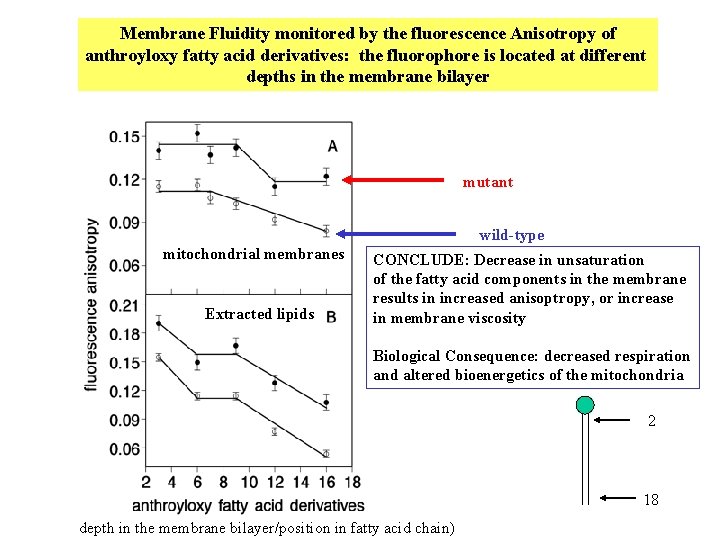
Membrane Fluidity monitored by the fluorescence Anisotropy of anthroyloxy fatty acid derivatives: the fluorophore is located at different depths in the membrane bilayer mutant wild-type mitochondrial membranes Extracted lipids CONCLUDE: Decrease in unsaturation of the fatty acid components in the membrane results in increased anisoptropy, or increase in membrane viscosity Biological Consequence: decreased respiration and altered bioenergetics of the mitochondria 2 18 depth in the membrane bilayer/position in fatty acid chain)

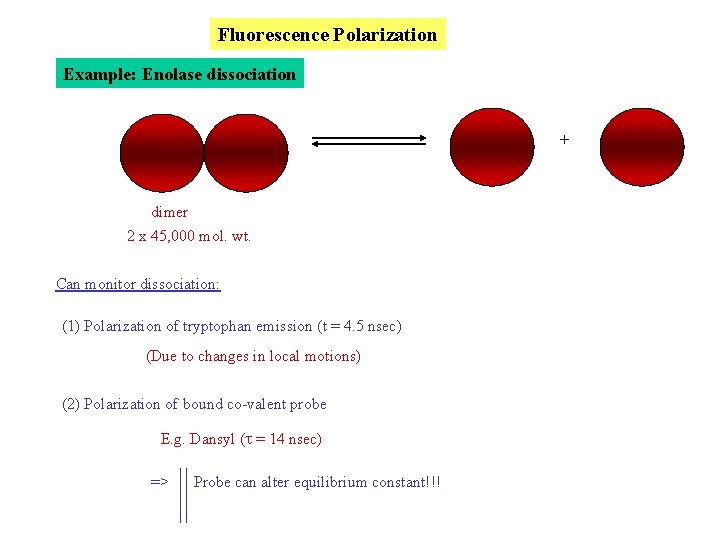
Fluorescence Polarization Example: Enolase dissociation + dimer 2 x 45, 000 mol. wt. Can monitor dissociation: (1) Polarization of tryptophan emission (t = 4. 5 nsec) (Due to changes in local motions) (2) Polarization of bound co-valent probe E. g. Dansyl (t = 14 nsec) => Probe can alter equilibrium constant!!!

+ D 2 M Let C 0 = total protein concentration as dimer [M]2 = 4 C 0 [a 2 / (1 - a)] [D] K= f. M = [M] 2 C 0 [D] C 0 f. D = Where a = degree of dissociation a= [M] + 2[D] = [M] 2 C 0 A D ID + A M IM ID + I M from Monomer from Dimer Anisotropy: A = Fluorescence intensity From A => a => K

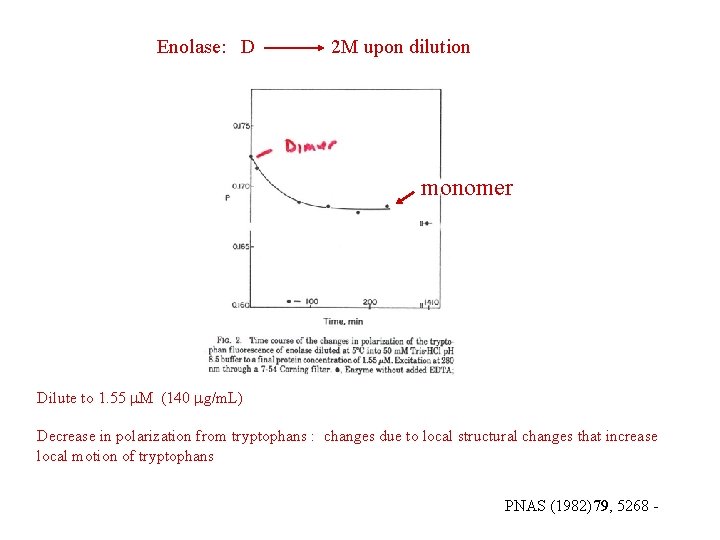
Enolase: D 2 M upon dilution monomer Dilute to 1. 55 M (140 g/m. L) Decrease in polarization from tryptophans : changes due to local structural changes that increase local motion of tryptophans PNAS (1982)79, 5268 -

Enolase: Pressure - Induced dissociation Biochemistry (1981)20, 2587 - Dansyl conjugate: [C 0] = 5. 6 M + Favored at high pressure Lower molar volume due to more efficient packing of water at protein - interface region

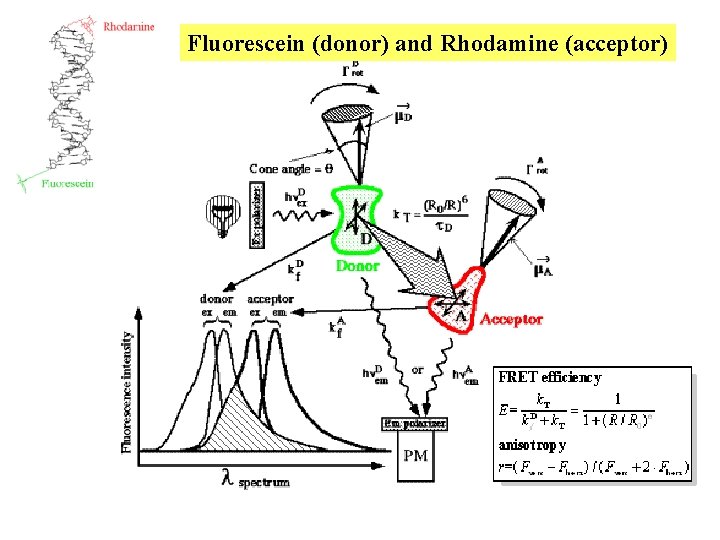
Fluorescein (donor) and Rhodamine (acceptor)

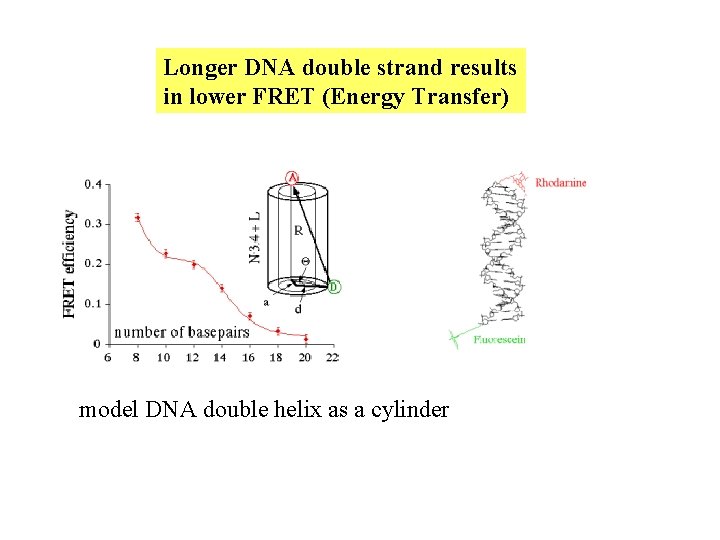
Longer DNA double strand results in lower FRET (Energy Transfer) model DNA double helix as a cylinder

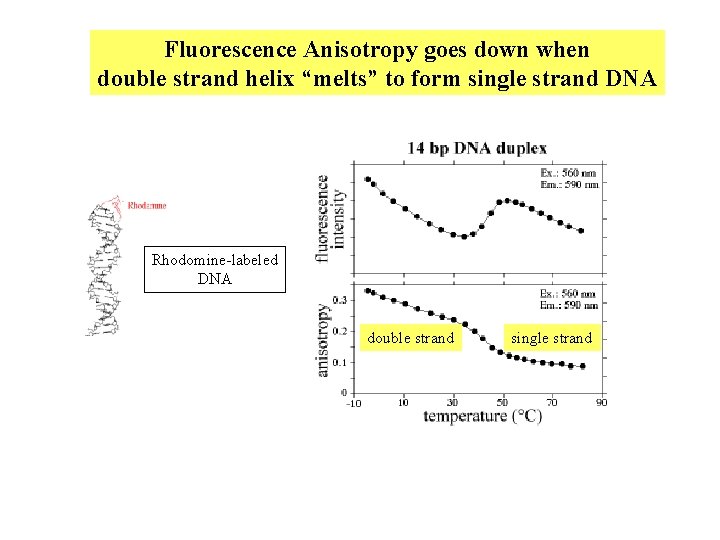
Fluorescence Anisotropy goes down when double strand helix “melts” to form single strand DNA Rhodomine-labeled DNA double strand single strand

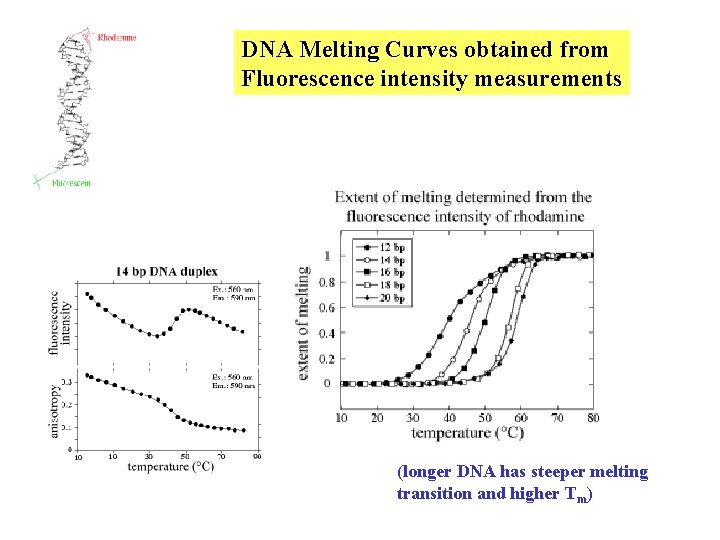
DNA Melting Curves obtained from Fluorescence intensity measurements (longer DNA has steeper melting transition and higher Tm)

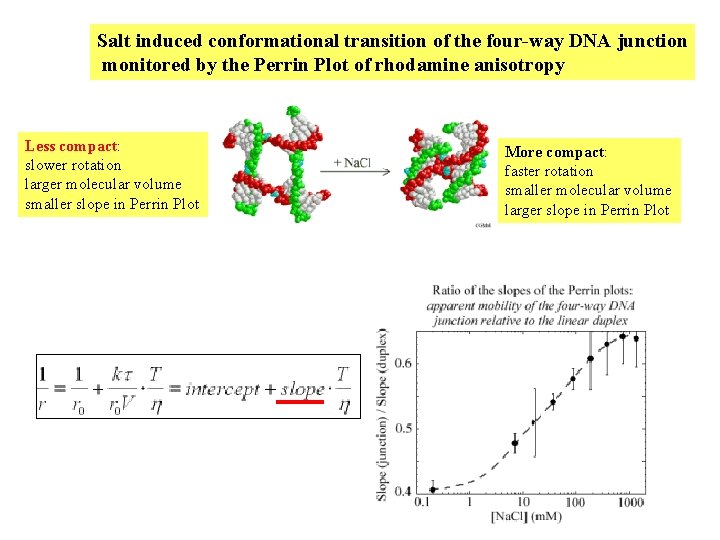
Salt induced conformational transition of the four-way DNA junction monitored by the Perrin Plot of rhodamine anisotropy Less compact: slower rotation larger molecular volume smaller slope in Perrin Plot More compact: faster rotation smaller molecular volume larger slope in Perrin Plot

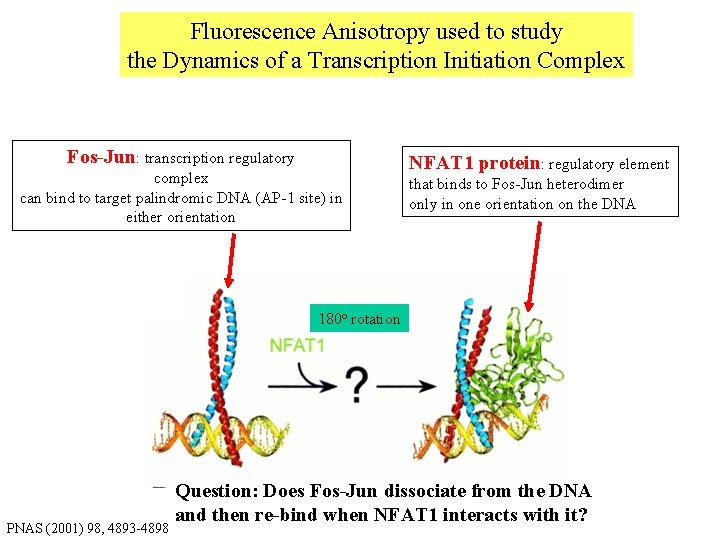
Fluorescence Anisotropy used to study the Dynamics of a Transcription Initiation Complex Fos-Jun: transcription regulatory complex can bind to target palindromic DNA (AP-1 site) in either orientation NFAT 1 protein: regulatory element that binds to Fos-Jun heterodimer only in one orientation on the DNA 180 o rotation PNAS (2001) 98, 4893 -4898 Question: Does Fos-Jun dissociate from the DNA and then re-bind when NFAT 1 interacts with it?

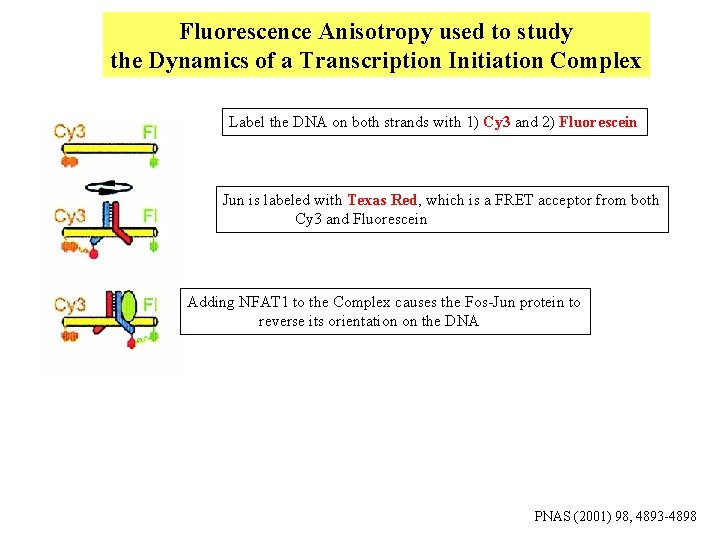
Fluorescence Anisotropy used to study the Dynamics of a Transcription Initiation Complex Label the DNA on both strands with 1) Cy 3 and 2) Fluorescein Jun is labeled with Texas Red, which is a FRET acceptor from both Cy 3 and Fluorescein Adding NFAT 1 to the Complex causes the Fos-Jun protein to reverse its orientation on the DNA PNAS (2001) 98, 4893 -4898

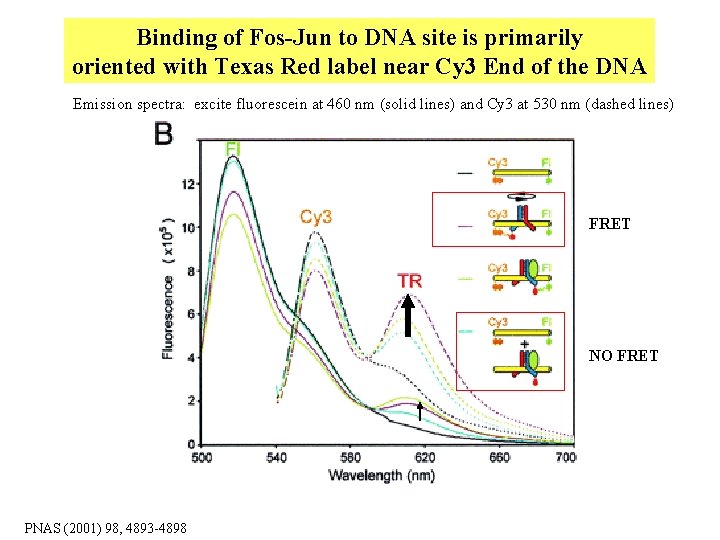
Binding of Fos-Jun to DNA site is primarily oriented with Texas Red label near Cy 3 End of the DNA Emission spectra: excite fluorescein at 460 nm (solid lines) and Cy 3 at 530 nm (dashed lines) FRET NO FRET PNAS (2001) 98, 4893 -4898

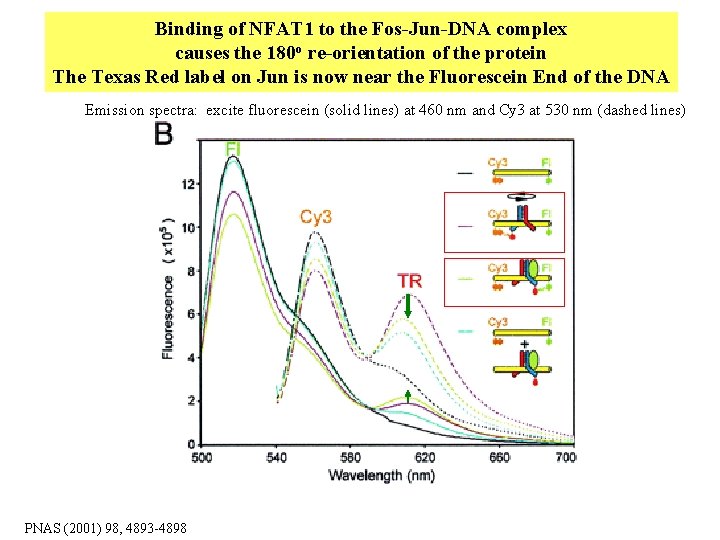
Binding of NFAT 1 to the Fos-Jun-DNA complex causes the 180 o re-orientation of the protein The Texas Red label on Jun is now near the Fluorescein End of the DNA Emission spectra: excite fluorescein (solid lines) at 460 nm and Cy 3 at 530 nm (dashed lines) PNAS (2001) 98, 4893 -4898

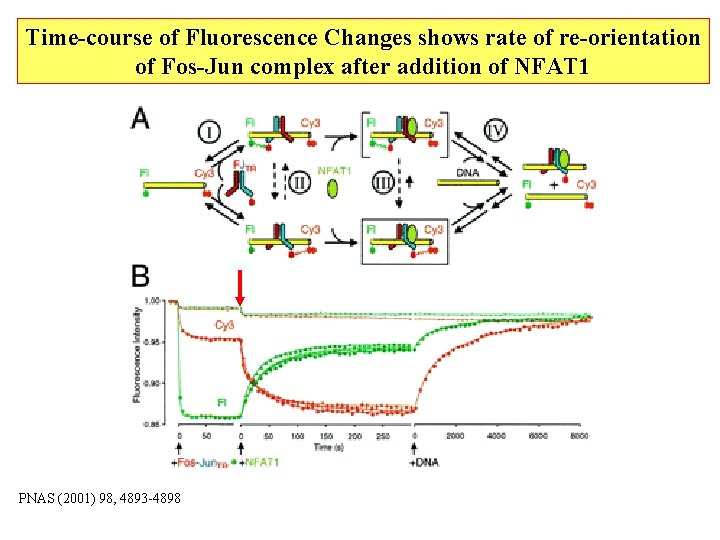
Time-course of Fluorescence Changes shows rate of re-orientation of Fos-Jun complex after addition of NFAT 1 PNAS (2001) 98, 4893 -4898

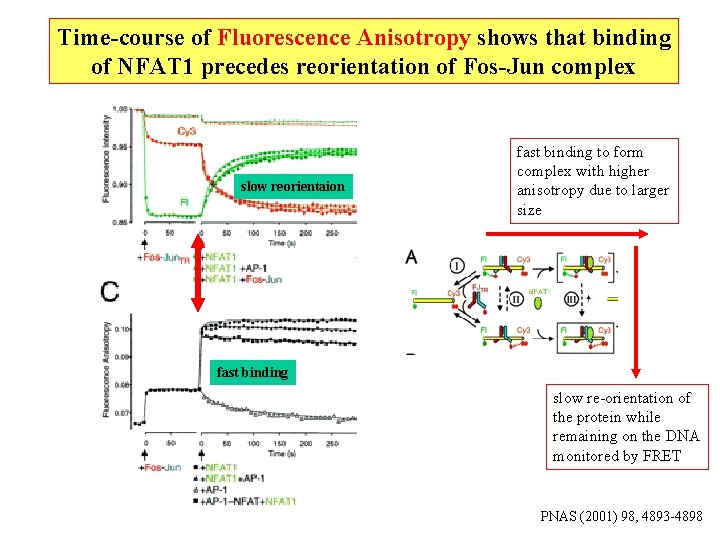
Time-course of Fluorescence Anisotropy shows that binding of NFAT 1 precedes reorientation of Fos-Jun complex slow reorientaion fast binding to form complex with higher anisotropy due to larger size fast binding slow re-orientation of the protein while remaining on the DNA monitored by FRET PNAS (2001) 98, 4893 -4898

Probing DNA structure and dynamics Fluorescein (donor) and Rhodamine (acceptor) http: //lfd. uiuc. edu/staff/gohlke/poster/#DNA junction

Rotational Diffusion Can model as a series of discontinuous jumps : <d 2> = 4 Drot dt start end units of sec-1 The “orientation vector” for a molecule is provided by the transition moment dipole oi Optical experiments - Absorption + Fluorescence provide information about molecular orientation oi q Probability of Absorption (or emission) cos 2 E

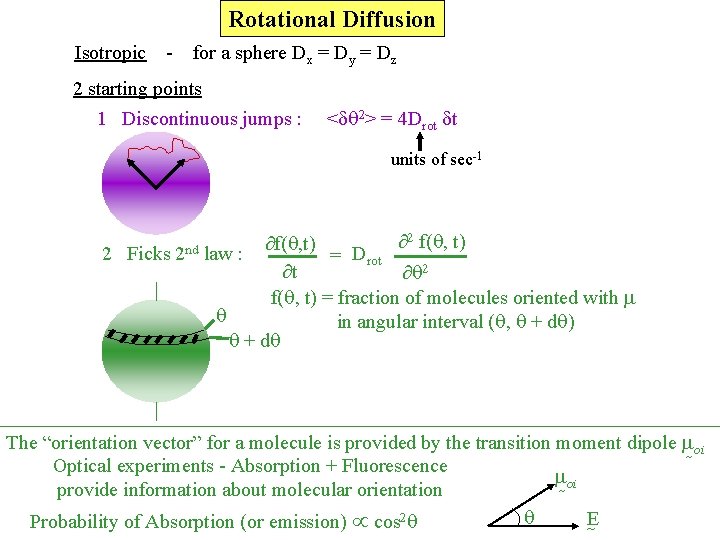
Rotational Diffusion Isotropic - for a sphere Dx = Dy = Dz 2 starting points 1 Discontinuous jumps : < q 2> = 4 Drot t units of sec-1 2 Ficks 2 nd 2 f(q, t) law : = Drot t q 2 f(q, t) = fraction of molecules oriented with q in angular interval (q, q + dq) q + dq The “orientation vector” for a molecule is provided by the transition moment dipole oi Optical experiments - Absorption + Fluorescence oi provide information about molecular orientation q E Probability of Absorption (or emission) cos 2 q

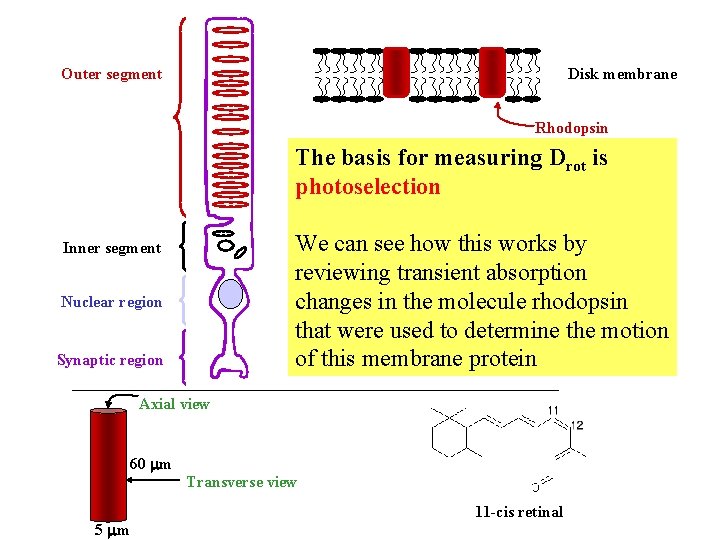
Outer segment Disk membrane Rhodopsin The basis for measuring Drot is photoselection We can see how this works by reviewing transient absorption changes in the molecule rhodopsin that were used to determine the motion of this membrane protein Inner segment Nuclear region Synaptic region Axial view 60 m Transverse view 5 m 11 -cis retinal

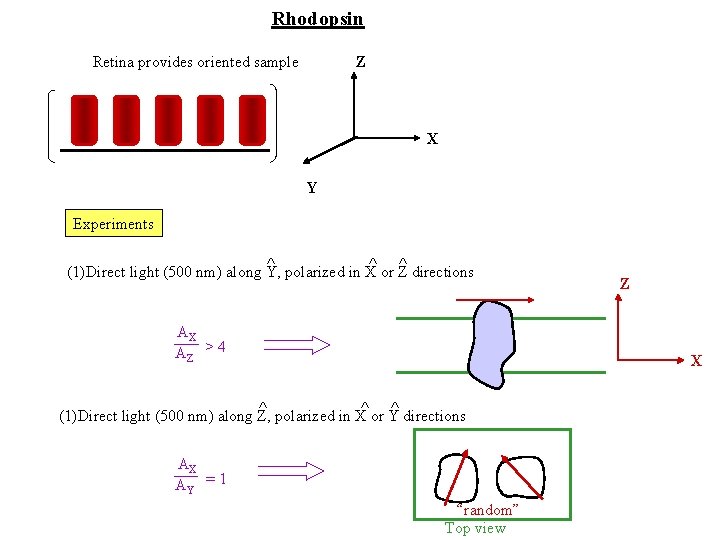
Rhodopsin Retina provides oriented sample Z X Y Experiments ^ ^ ^ (1)Direct light (500 nm) along Y, polarized in X or Z directions AX AZ > 4 Z X ^ ^ ^ (1)Direct light (500 nm) along Z, polarized in X or Y directions AX AY = 1 “random” Top view

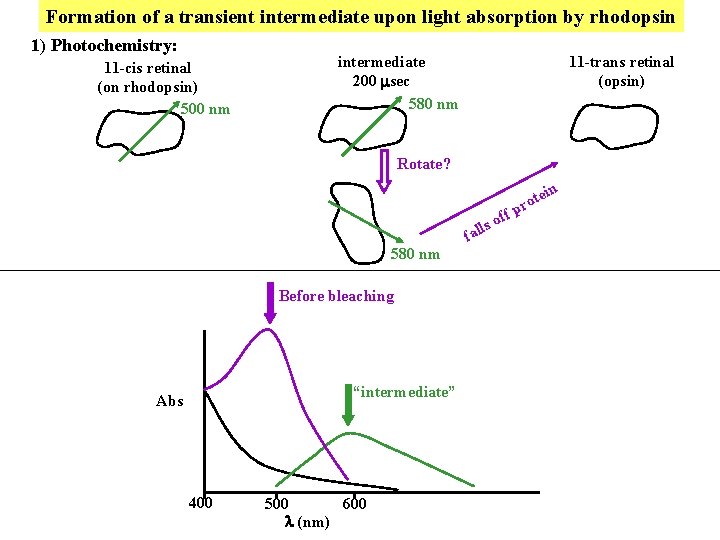
Formation of a transient intermediate upon light absorption by rhodopsin 1) Photochemistry: 11 -cis retinal (on rhodopsin) 500 nm intermediate 200 sec 580 nm 11 -trans retinal (opsin) Rotate? in ff o lls 580 nm Before bleaching “intermediate” Abs 400 500 600 l (nm) fa te pro

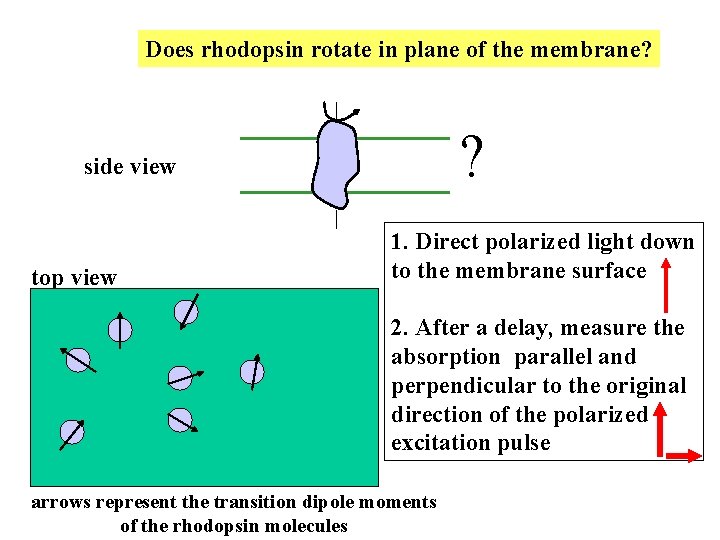
Does rhodopsin rotate in plane of the membrane? ? side view top view 1. Direct polarized light down to the membrane surface 2. After a delay, measure the absorption parallel and perpendicular to the original direction of the polarized excitation pulse arrows represent the transition dipole moments of the rhodopsin molecules

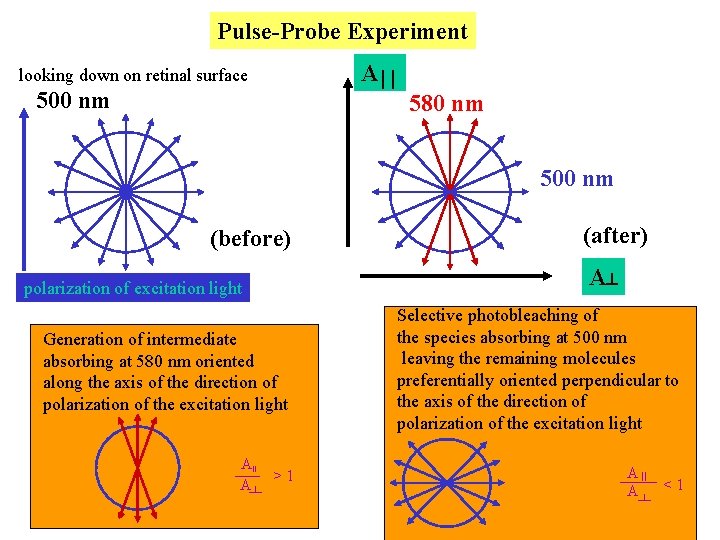
Pulse-Probe Experiment A looking down on retinal surface 500 nm 580 nm 500 nm (before) A polarization of excitation light Generation of intermediate absorbing at 580 nm oriented along the axis of the direction of polarization of the excitation light AII A (after) >1 Selective photobleaching of the species absorbing at 500 nm leaving the remaining molecules preferentially oriented perpendicular to the axis of the direction of polarization of the excitation light A II <1 A

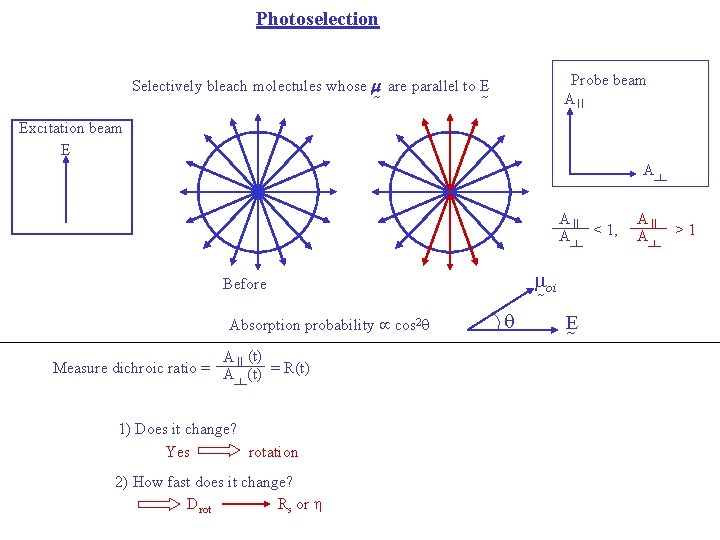
Photoselection Probe beam A II Selectively bleach molectules whose m are parallel to E Excitation beam E A A II A < 1, oi Before Absorption probability cos 2 q A (t) Measure dichroic ratio = A II (t) = R(t) 1) Does it change? Yes rotation 2) How fast does it change? Drot Rs or q E A II A >1

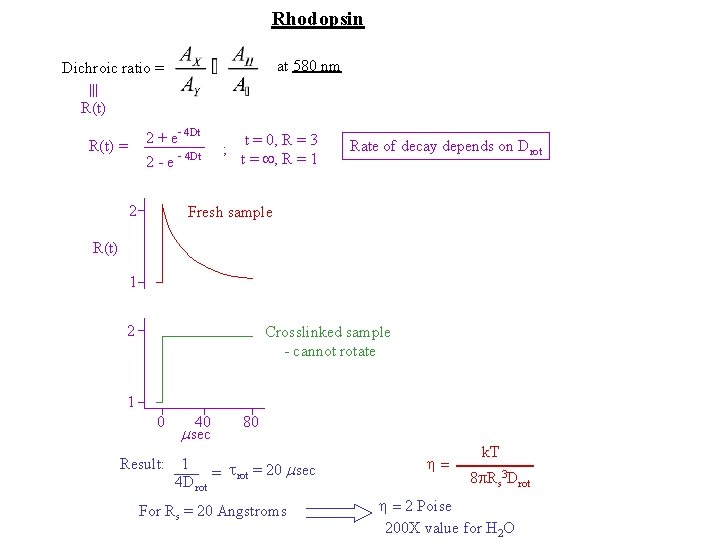
Rhodopsin at 580 nm Dichroic ratio = R(t) 2 + e- 4 Dt R(t) = 2 -e 2 - 4 Dt ; t = 0, R = 3 t = , R = 1 Rate of decay depends on Drot Fresh sample R(t) 1 2 Crosslinked sample - cannot rotate 1 0 40 msec 80 Result: 1 = trot = 20 msec 4 Drot For Rs = 20 Angstroms = k. T 8 p. Rs 3 Drot = 2 Poise 200 X value for H 2 O

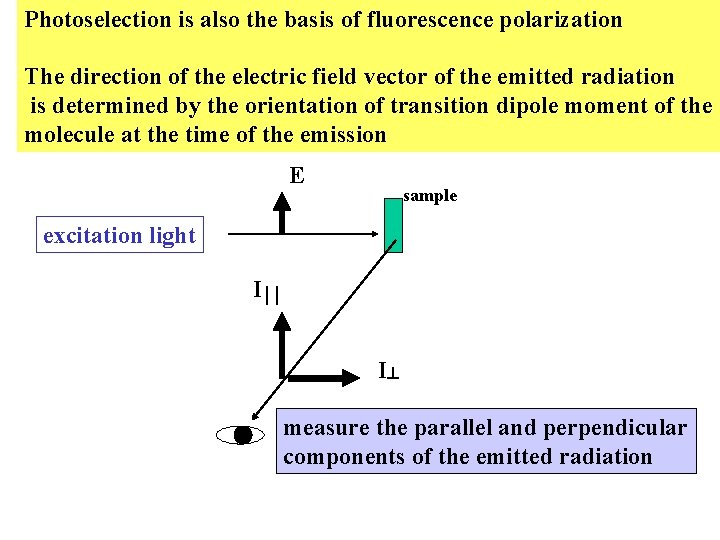
Photoselection is also the basis of fluorescence polarization The direction of the electric field vector of the emitted radiation is determined by the orientation of transition dipole moment of the molecule at the time of the emission E sample excitation light I I measure the parallel and perpendicular components of the emitted radiation

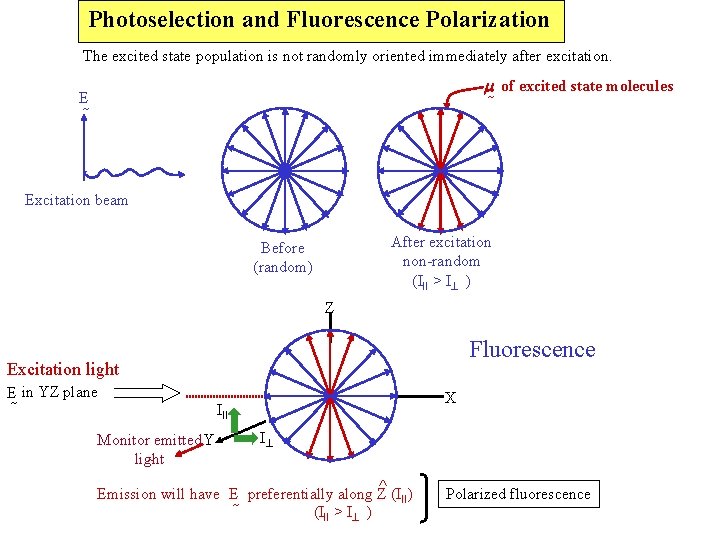
Photoselection and Fluorescence Polarization The excited state population is not randomly oriented immediately after excitation. m of excited state molecules E Excitation beam After excitation non-random (III > I ) Before (random) Z Fluorescence Excitation light E in YZ plane Monitor emitted Y light X III I ^ Emission will have E preferentially along Z (III) (III > I ) Polarized fluorescence

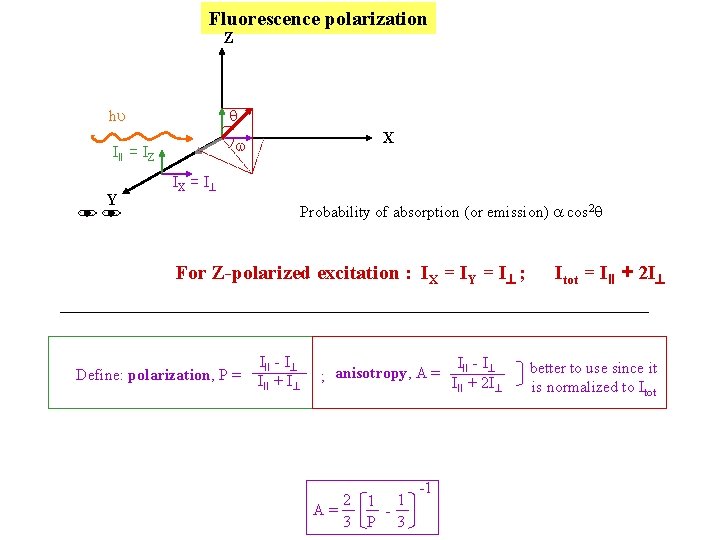
Fluorescence polarization Z q hu III = IZ Y X w IX = I Probability of absorption (or emission) a cos 2 q For Z-polarized excitation : IX = IY = I ; Define: polarization, P = III - I III + I III - I ; anisotropy, A = I + 2 I II 2 1 1 A= 3 P 3 -1 Itot = III + 2 I better to use since it is normalized to Itot

Measured anisotropy from multiple fluorescing species is a weighted sum of the anisotropies of the component species A= III - I III + 2 I = III - I Itotal If multiple species contribute to fluorescence: A= I 1 A 1 + I 2 A 2 + I 3 A 3 I 1 + I 2 + I 3 A = f 1 A 1 + f 2 A 2 + f 3 A 3 fraction of fluorescence from species 1 A simple weighted average

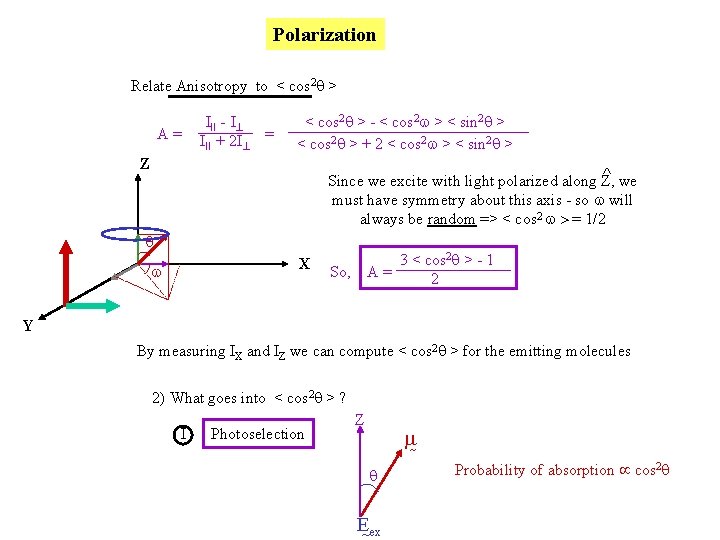
Polarization Relate Anisotropy to < cos 2 q > A= III - I III + 2 I = < cos 2 q > - < cos 2 w > < sin 2 q > < cos 2 q > + 2 < cos 2 w > < sin 2 q > Z ^ we Since we excite with light polarized along Z, must have symmetry about this axis - so w will always be random => < cos 2 w > = 1/2 q X w 3 < cos 2 q > - 1 A= 2 So, Y By measuring IX and IZ we can compute < cos 2 q > for the emitting molecules 2) What goes into < cos 2 q > ? I Photoselection Z q E ex Probability of absorption cos 2 q

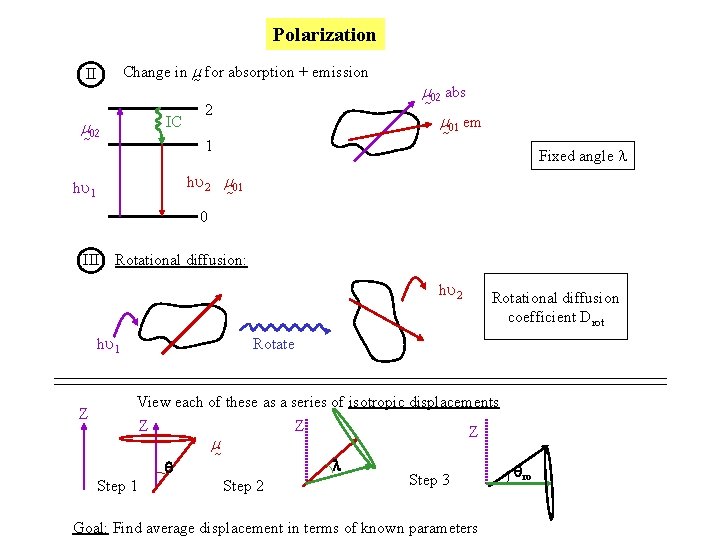
Polarization Change in m for absorption + emission II IC m 02 2 m 02 abs m 01 em 1 Fixed angle l hu 2 m 01 hu 1 0 III Rotational diffusion: hu 2 hu 1 Z Rotational diffusion coefficient Drot Rotate View each of these as a series of isotropic displacements Z Step 1 Z m Z l Step 2 Step 3 Goal: Find average displacement in terms of known parameters ro